Теория вероятностей и математическая статистика Тема 11 Проверка

Теория вероятностей и математическая статистика Тема 11. Проверка статистических гипотез

Лекция 17 Проверка статистических гипотез • Сложные параметрические гипотезы • Проверка гипотезы о равенстве двух выборочных средних. • Проверка гипотезы о равенстве дисперсий двух совокупностей. Тема 11. Проверка статистических гипотез

Литература [1]. С. 189 -194 [2]. С. 171 -178 [1]. В. А. Фигурин, В. В. Оболонкин, Теория вероятностей и математическая статистика; ООО "Новое знание": Минск, 2000. [2]. Горяинов, В. Б. , и др. , Математическая статистика, п/р. В. С. Зарубин and А. П. Крищенко. 2001, М. : Издательство МГТУ им. Н. Э. Баумана. 424. Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы В общем случае, Θ 0, Θ 1 – непересекающиеся области параметра θ. Области, например, могут быть заданы θ ≤ θ 0 , θ ≥θ 1 , где θ 0, θ 1 – некоторые фиксированные значения параметра, для которых выполняется неравенство θ 0<θ 1 (сравнение с примером). Критерий проверки по-прежнему задается с помощью критического множества W реализаций случайной выборки . Решение принимают следующим образом. 1. Выборка принадлежит W. Отвергают H 0. Принимают H 1. 2. Выборка не принадлежит W (принадлежит дополнению множества W до выборочного пространства). Отвергают H 1. Принимают H 0. Тема 11. Проверка статистических гипотез

. Сложные параметрические гипотезы Вероятности совершения ошибок первого и второго рода имеют прежний смысл. В отличие от простых гипотез α и β – функции параметра α(θ) β(θ). Максимально возможное значение вероятности совершения ошибки первого рода называется размером критерия. Функция, определяющая значение вероятности отклонения основной гипотезы H 0 в зависимости от истинного значения параметра θ, называется функцией мощности критерия Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы Если существует критерий, который при данном фиксированном размере α максимизирует функцию мощности M(θ) по всем возможным критериям одновременно при всех θ из множества Θ 1 , то такой критерий называют равномерно наиболее мощным. Равномерно наиболее мощные критерии существуют лишь для некоторых частных случаев. Параметры α(θ) и β(θ) связаны с M(θ) То есть равномерно наиболее мощный критерий минимизирует вероятность совершения ошибки второго рода β(θ) при фиксированном размере α одновременно при всех θ из множества Θ 1. Иногда наряду с функцией мощности используется также оперативная характеристика критерия, представляющая собой вероятность принятия основной гипотезы H 0 при условии, что истинное значение параметра равно θ Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 1. Рассмотрим проверку простой гипотезы против сложной относительно среднего μ нормального закона распределения с извесной дисперсией σ2. H 0: μ=μ 0 H 1: μ> μ 0 При любом μ 1 >μ 0 критическая область оптимального наиболее мощного критерия Неймана-Пирсона размера α для простых гипотез H 0: μ=μ 0 против H 1: μ=μ 1 (рассмотренных на предыдущей лекции) имеет вид Константу выбирают из условия Или Константа не зависит от μ 1. Это означает, что построенный выше критерий с критичским множество, задаваемым Является равномерно наиболее мощным критерием размера α для данной задачи со сложной альтернативной гипотезой. H 1: μ> μ 0 Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 2. Рассмотрим проверку простой гипотезы против сложной относительно среднего μ нормального закона распределения с извесной дисперсией σ2. H 0: μ=μ 0 H 1: μ< μ 0 В этом случае также используем результаты предыдущей лекции и предыдущего примера. Равномерно наиболее мощный критерий размера α для данной задачи задается критическим множеством, определяемым неравенством. Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 3. Рассмотрим проверку двух сложных гипотез относительно среднего μ нормального закона распределения с извесной дисперсией σ2. H 0: μ≤μ 0 H 1: μ≥ μ 1 Причем, μ 0< μ 1 Для критерия с критическим множеством вероятность совершения ошибки первого рода – возрастающая функция µ. Максимальное значение вероятности совершения ошибки первого рода достигается в точке μ=μ 0, отсюда следует, что данный критерий, применяемый к сложным гипотезам, имеет размерность α= α(µ 0) Рассуждая аналогично предыдущим примерам, получаем, что указанный критерий является равномерно наиболее мощным критерием для данной задачи со сложными гипотезами. Критическая область определяется Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 4. Рассмотрим проверку гипотез относительно среднего μ нормального закона распределения с извесной дисперсией σ2. H 0: μ=μ 0 H 1: μ≠ μ 1 Первая гипотеза – простая, вторая сложная. Рассмотрим статистику Статистика имеет нормальное распределением. Критическое множество для проверки гипотез определяется Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 5. Рассмотрим проверку 2 сложных гипотез против относительно среднего μ нормального закона распределения с неизвесной дисперсией σ2. H 0: μ=μ 0 H 1: μ> μ 0 Рассматриваем статистику, которая имеет распределение Стьюдента с n-1 степенями свободы Критерий уровня значимости α задается критическим множеством c соответствующими квантилями распределения Стьюдента Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 6. Рассмотрим проверку 2 сложных гипотез против относительно среднего μ нормального закона распределения с неизвесной дисперсией σ2. H 0: μ=μ 0 H 1: μ< μ 0 Аналогично предыдущему примеру критерий уровня значимости α задается критическим множеством c соответствующими квантилями распределения Стьюдента Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 8. Рассмотрим проверку 2 сложных гипотез о равенстве математических ожиданий 2 нормальных распределений с извесными дисперсиями σ2. Пусть определены две случайные выборки (X 1, . . . Xn) (Y 1, . . . , Ym) объемов m и n из генеральной совокупностей независимых случайных величин и Рассмотрим следующие гипотезы H 0: μ 1=μ 2 H 1: μ 1>μ 2 H 0: μ 1=μ 2 H 1: μ 1<μ 2 H 0: μ 1=μ 2 H 1: μ 1≠μ 2 Разность выборочных средних имеет нормальное распределение с математическим ожиданием μ -μ 1 2 и дисперсией При справедливости основной гипотезы статистика имеет нормальное распределение Соответсвующие критерии выглядят следующим образом Тема 11. Проверка статистических гипотез

Сложные параметрические гипотезы. Примеры Пример 9. Рассмотрим проверку 2 сложных гипотез о равенстве дисперсий 2 нормальных распределений. H 0: σ21=σ22 H 1: σ21=σ22 Для построения критического множенства используем статистику, имеющую распределение Фишера со степенями свободы n-1, m-1 Соответсвующие критерии выглядят следующим образом где f- квантиль соответствующего распределения. Тема 11. Проверка статистических гипотез

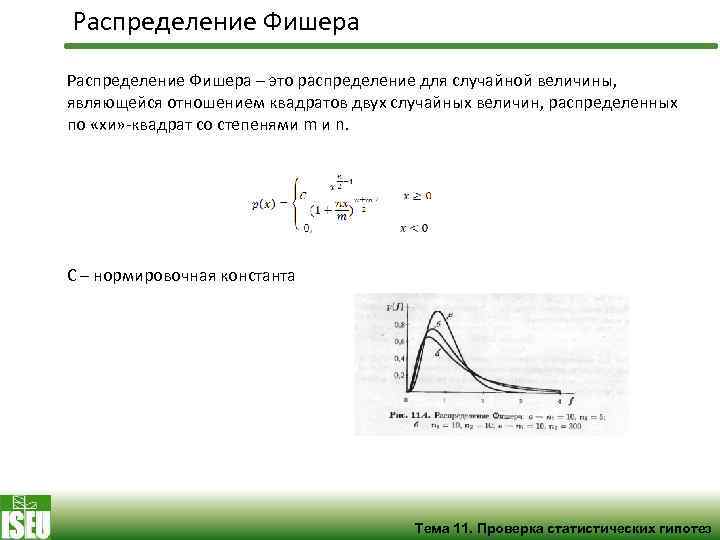Распределение Фишера – это распределение для случайной величины, являющейся отношением квадратов двух случайных величин, распределенных по «хи» -квадрат со степенями m и n. C – нормировочная константа Тема 11. Проверка статистических гипотез