Теория вероятностей и математическая статистика Основные теоремы исчисления

Независимые события Определение События A и B называются независимыми, если

Пример Из колоды, насчитывающей 36 карт, наугад извлекается карта. Будут ли события {извлекли даму}

Замечание Если события A и B несовместны, то они независимы только если P(A) =

Условная вероятность Вероятность события A, вычисленную в предположении, что событие B произошло, мы будем

Определение Условной вероятностью события A при условии, что произошло событие B, называется число Считают,

Пример Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом

B = {4,5,6}, p(B) = 3/6 = 1/2, AB = {4,6}, p(AB) = 2/6

Свойства независимых событий Если события A и B независимы, то: P(A|B) = P(A), P(B|A)

Независимость в совокупности Определение События A1, A2, …, An называются независимыми в совокупности, если

Замечание Если события A1, A2, …, An независимы в совокупности, то они попарно независимы,

Пример Из колоды, насчитывающей 36 карт, наугад извлекается карта. Какова вероятность, что это дама

Теорема умножения для двух событий если соответствующие условные вероятности определены (то есть если P(A)

Теорема умножения для n событий Доказательство проводится по индукции.

Пример Из букв слова «МАТЕМАТИКА» случайно выбирают 4 буквы и выкладывают в ряд. Найти

Гипотезы Определение Набор попарно несовместных событий H1, H2, …, Hn таких, что P(Hi) >

Теорема (формула полной вероятности) Пусть A – случайное событие, H1, H2, …, Hn –

Пример Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод

Решение Рассмотрим три гипотезы: Hi = {изделие произведено i-м заводом}, i = 1,2,3. Вероятности

Полная вероятность равна доле бракованных изделий в объеме всей продукции.

Теорема (Формула Байеса) Пусть A – случайное событие, H1, H2, …, Hn – полная

Пример По условиям предыдущего примера, найти вероятность, что изделие изготовлено первым заводом, при условии,

Тогда вероятность того, что бракованное изделие произведено первым заводом, будет равна

Схемы испытаний Схема Бернулли. Предельные теоремы

Схема Бернулли Определение Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны

Теорема (формула Бернулли) Обозначим через m число успехов в n испытаниях схемы Бернулли. Тогда

Поскольку испытания независимы, вероятность такого элементарного исхода равна Другие благоприятствующие событию A элементарные исходы

Поэтому событие A состоит из элементарных исходов, вероятность каждого из которых равна т.е.

Наивероятнейшее число успехов В испытаниях схемы Бернулли наиболее вероятным числом успехов является a) единственное

Пример Вычислить вероятности всех возможных значений появления «герба» при 5 бросаниях монеты. Построить график

Наивероятнейшее число успехов: Вычисляем np + p = 5∙1/2 + ½ = 3. Это

Еще один пример Вероятность сдать экзамен равна 0,8. Найти наивероятнейшее число студентов, сдавших экзамен

Полиномиальная схема Определение Полиномиальной схемой называется последовательность n независимых одинаковых испытаний, в каждом из

Пример Человек с вероятностью 0,2 оказывается брюнетом, с вероятностью 0,4 —шатеном, с вероятностью 0,3

Гипергеометрические испытания Пусть из совокупности n предметов, среди которых n1 предметов первого вида и

Гипергеометрические вероятности Данные испытания являются зависимыми.

Пример В урне 6 белых и 5 черных шаров. Из урны вынимают наугад 5

Предельные теоремы для схемы Бернулли При числе испытаний, превышающем 20, вычисление точного значения Pn(m)

Теорема Пуассона Если n  , р  0 так, что np  ,

Приближенная формула Пуассона где  = np. Приближенную формулу Пуассона применяют при n >

Пример (дни рождения) Какова вероятность, что среди 500 случайно выбранных людей ни один не

Предельная теорема Муавра –Лапласа Если при n  и постоянном р, не равном 0

Доказательство этой теоремы основано на применении формулы Стирлинга

Локальная приближенная формула Муавра –Лапласа Локальную приближенную формулу Муавра – Лапласа применяют при n

График биномиальных вероятностей при n=30, p=0,2 и график φ(X)

Интегральная предельная теорема Муавра –Лапласа При n  и постоянном р, не равном 0

Интегральная приближенная формула Муавра –Лапласа Интегральную приближенную формулу Муавра – Лапласа применяют при n

Функция Лапласа Φ0(x). Вместо Φ(x) часто используют функцию Лапласа Φ0(x).

Замечания поэтому в формулах может использоваться как Φ(x), так и Φ0(x). Значения функций находят

Пример Вероятность рождения мальчика p = 0,5. Найти вероятность того, что в группе из

Скачать презентацию Теория вероятностей и математическая статистика Основные теоремы исчисления

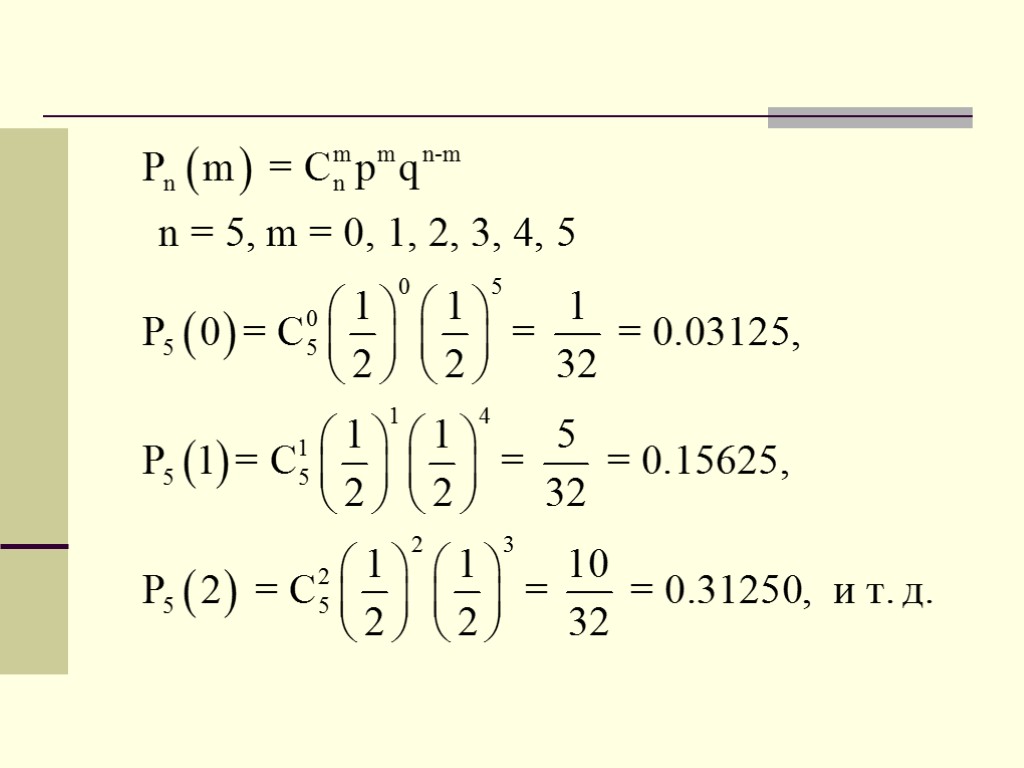
2011lectvec2_ec.ppt

Количество слайдов: 63

>Теория вероятностей и математическая статистика Основные теоремы исчисления вероятностей 2 Теория вероятностей и математическая статистика Основные теоремы исчисления вероятностей 2

>Независимые события Определение События A и B называются независимыми, если Независимые события Определение События A и B называются независимыми, если

>Пример Из колоды, насчитывающей 36 карт, наугад извлекается карта. Будут ли события {извлекли даму} Пример Из колоды, насчитывающей 36 карт, наугад извлекается карта. Будут ли события {извлекли даму} и {извлекли пику} независимы? Решение. A = {дама}, B = {пика}, AB = {дама пик}. p(A) = 4/36 = 1/9, p(B) = 9/36 = 1/4, p(AB) = 1/36. p(A) ∙ p(B) = 1/9 ∙ 1/4 = 1/36. p(A) ∙ p(B) = p(AB) → A и B независимы.

>Замечание Если события A и B несовместны, то они независимы только если P(A) = Замечание Если события A и B несовместны, то они независимы только если P(A) = 0 или P(B) = 0. (ПОЧЕМУ?)

>Условная вероятность Вероятность события A, вычисленную в предположении, что событие B произошло, мы будем Условная вероятность Вероятность события A, вычисленную в предположении, что событие B произошло, мы будем обозначать через

>Определение Условной вероятностью события A при условии, что произошло событие B, называется число Считают, Определение Условной вероятностью события A при условии, что произошло событие B, называется число Считают, что условная вероятность определена только в случае, когда P(B) > 0.

>Пример Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом Пример Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков? Решение.  при одном подбрасывании кубика состоит из шести точек:  = {1, 2, 3, 4, 5, 6}. Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие B = {4, 5, 6}.

>B = {4,5,6}, p(B) = 3/6 = 1/2, AB = {4,6}, p(AB) = 2/6 B = {4,5,6}, p(B) = 3/6 = 1/2, AB = {4,6}, p(AB) = 2/6 = 1/3.

>Свойства независимых событий Если события A и B независимы, то: P(A|B) = P(A), P(B|A) Свойства независимых событий Если события A и B независимы, то: P(A|B) = P(A), P(B|A) = P(B) (если P(A) >0, P(B) > 0). независимы и события

>Независимость в совокупности Определение События A1, A2, …, An называются независимыми в совокупности, если Независимость в совокупности Определение События A1, A2, …, An называются независимыми в совокупности, если для любого набора событий вероятность произведения равна произведению вероятностей:

>Замечание Если события A1, A2, …, An независимы в совокупности, то они попарно независимы, Замечание Если события A1, A2, …, An независимы в совокупности, то они попарно независимы, т.е. любые два события Ai, Aj независимы. (ПОЧЕМУ?) Обратное неверно. Если события попарно независимы, то в совокупности могут быть зависимы.

>Теорема сложения Для 2-х событий: Теорема сложения Для 2-х событий:

>Пример Из колоды, насчитывающей 36 карт, наугад извлекается карта. Какова вероятность, что это дама Пример Из колоды, насчитывающей 36 карт, наугад извлекается карта. Какова вероятность, что это дама или пика? Решение. A = {дама}, B = {пика}, A+B = {дама или пика}, AB = {дама пик}. p(A) = 4/36, p(B) = 9/36, p(AB) = 1/36. p(A+B) = p(A) + p(B) – p(AB) = 4/36 + 9/36 – 1/36 = 12/36 = 1/3.

>Теорема сложения для n событий Теорема сложения для n событий

>Теорема умножения для двух событий если соответствующие условные вероятности определены (то есть если P(A) Теорема умножения для двух событий если соответствующие условные вероятности определены (то есть если P(A) > 0, P(B) > 0). Доказательство следует из определения условной вероятности.

>Пример Из букв слова Пример Из букв слова "ВЕРОЯТНОСТЬ" случайно выбирают 2 буквы. Найти вероятность того, что выбраны 2 буквы "О". Решение.

>Теорема умножения для n событий Доказательство проводится по индукции. Теорема умножения для n событий Доказательство проводится по индукции.

>Пример Из букв слова «МАТЕМАТИКА» случайно выбирают 4 буквы и выкладывают в ряд. Найти Пример Из букв слова «МАТЕМАТИКА» случайно выбирают 4 буквы и выкладывают в ряд. Найти вероятность того, что получится слово «ТЕМА».

>Гипотезы Определение Набор попарно несовместных событий H1, H2, …, Hn таких, что P(Hi) > Гипотезы Определение Набор попарно несовместных событий H1, H2, …, Hn таких, что P(Hi) > 0 для всех i и называется полной группой событий. События, образующие полную группу событий, называются гипотезами.

>Теорема (формула полной вероятности) Пусть A – случайное событие, H1, H2, …, Hn – Теорема (формула полной вероятности) Пусть A – случайное событие, H1, H2, …, Hn – полная группа событий (гипотезы), Тогда вероятность события А может быть вычислена по формуле:

>Доказательство Доказательство

>Пример Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод Пример Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод – 35% и 3-й завод – 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода. Найти вероятность купить бракованное изделие.

>Решение Рассмотрим три гипотезы: Hi = {изделие произведено i-м заводом}, i = 1,2,3. Вероятности Решение Рассмотрим три гипотезы: Hi = {изделие произведено i-м заводом}, i = 1,2,3. Вероятности этих событий даны: P(H1) = 0,25, P(H2) = 0,35, P(H3) = 0,4. Пусть A = {изделие бракованное}. Причем даны условные вероятности: P(A|H1) = 0,05, P(A|H2) = 0,03, P(A|H3) = 0,04.

>Полная вероятность равна доле бракованных изделий в объеме всей продукции. Полная вероятность равна доле бракованных изделий в объеме всей продукции.

>Теорема (Формула Байеса) Пусть A – случайное событие, H1, H2, …, Hn – полная Теорема (Формула Байеса) Пусть A – случайное событие, H1, H2, …, Hn – полная группа событий (гипотезы), Тогда условная вероятность того, что имело место событие Hk, если наблюдалось событие А, может быть вычислена по формуле:

>Доказательство Доказательство

>Пример По условиям предыдущего примера, найти вероятность, что изделие изготовлено первым заводом, при условии, Пример По условиям предыдущего примера, найти вероятность, что изделие изготовлено первым заводом, при условии, что оно бракованное. Решение Рассмотрим три гипотезы: Hi = {изделие произведено i заводом}, I = 1,2,3. Вероятности этих событий даны: P(H1) = 0,25, P(H2) = 0,35, P(H3) = 0,4. Пусть A = {изделие бракованное}. Условные вероятности: P(A|H1) = 0,05, P(A|H2) = 0,03, P(A|H3) = 0,04.

>Тогда вероятность того, что бракованное изделие произведено первым заводом, будет равна Тогда вероятность того, что бракованное изделие произведено первым заводом, будет равна

>Схемы испытаний Схема Бернулли. Предельные теоремы Схемы испытаний Схема Бернулли. Предельные теоремы

>Схема Бернулли Определение Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны Схема Бернулли Определение Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» и «неудача», при этом «успех» в одном испытании происходит с вероятностью p, а «неудача» — с вероятностью q = 1 – p.

>Теорема (формула Бернулли) Обозначим через m число успехов в n испытаниях схемы Бернулли. Тогда Теорема (формула Бернулли) Обозначим через m число успехов в n испытаниях схемы Бернулли. Тогда Доказательство Событие A = {число успехов равно m} означает, что в n испытаниях схемы Бернулли произошло ровно m успехов. Рассмотрим один из благоприятных исходов:

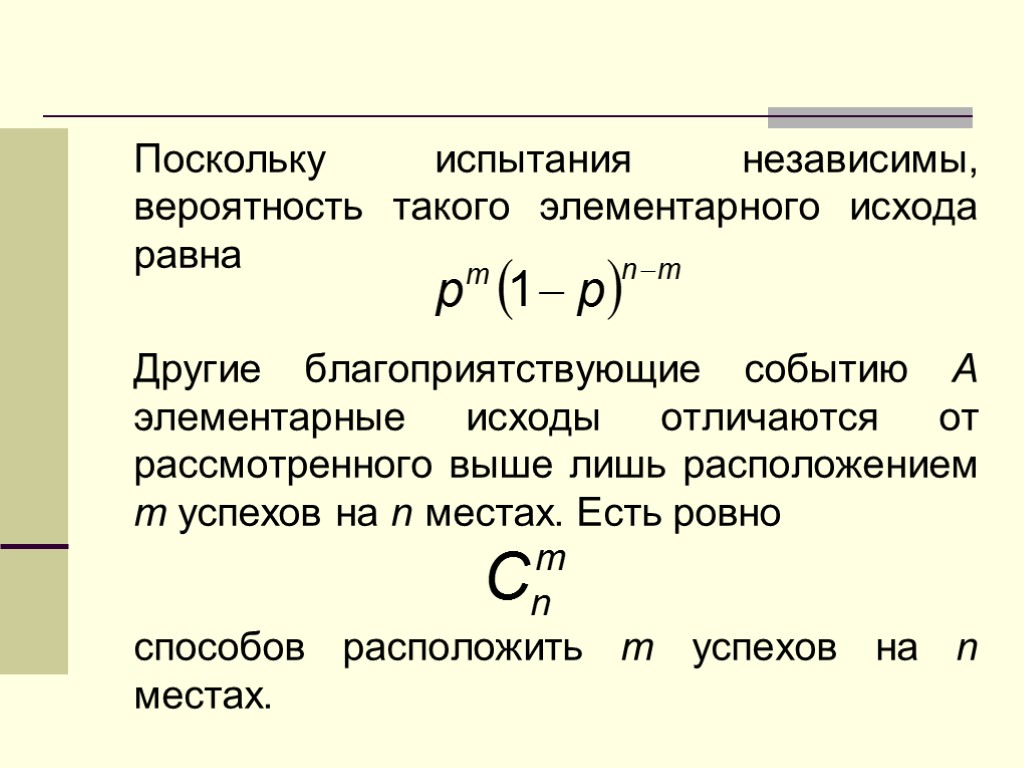
>Поскольку испытания независимы, вероятность такого элементарного исхода равна Другие благоприятствующие событию A элементарные исходы Поскольку испытания независимы, вероятность такого элементарного исхода равна Другие благоприятствующие событию A элементарные исходы отличаются от рассмотренного выше лишь расположением m успехов на n местах. Есть ровно способов расположить m успехов на n местах.

>Поэтому событие A состоит из элементарных исходов, вероятность каждого из которых равна т.е. Поэтому событие A состоит из элементарных исходов, вероятность каждого из которых равна т.е.

>Наивероятнейшее число успехов В испытаниях схемы Бернулли наиболее вероятным числом успехов является a) единственное Наивероятнейшее число успехов В испытаниях схемы Бернулли наиболее вероятным числом успехов является a) единственное число m0 = [np + p] (целая часть), если число np + p не целое; б) два числа m0 = np + p и m0' = np + p – 1, если число np + p целое.

>Пример Вычислить вероятности всех возможных значений появления «герба» при 5 бросаниях монеты. Построить график Пример Вычислить вероятности всех возможных значений появления «герба» при 5 бросаниях монеты. Построить график распределения этих вероятностей. Решение Число независимых испытаний n = 5. Число успехов m = 0, 1, 2, 3, 4, 5. Вероятность успеха в одном испытании p = 0,5.

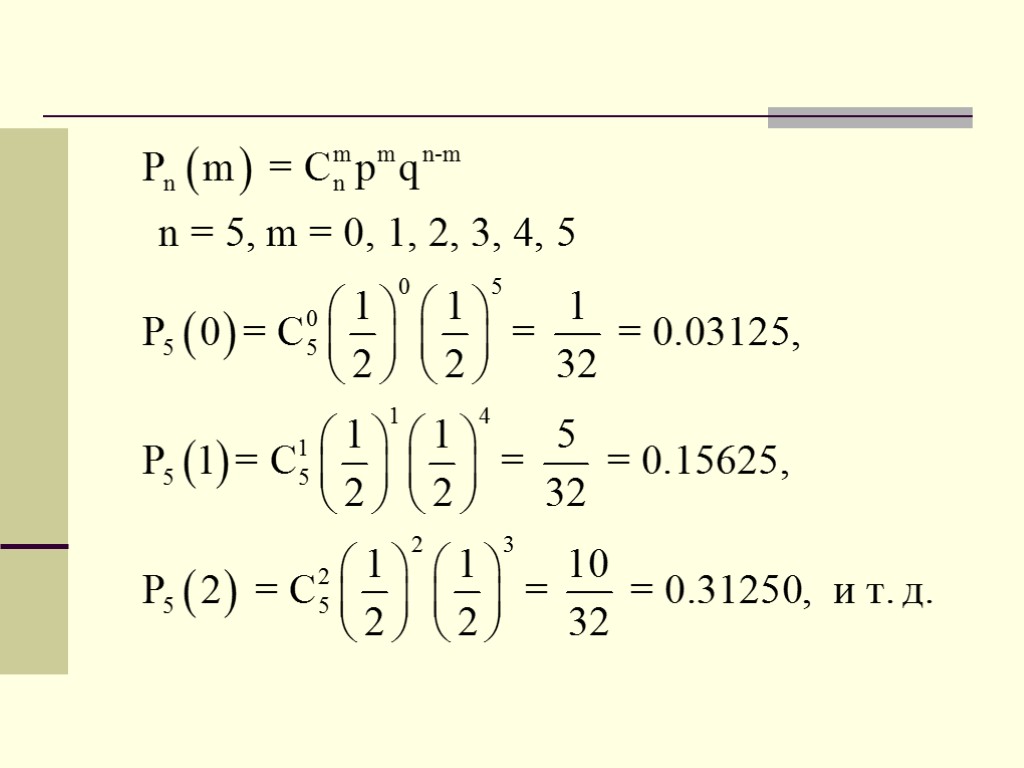
>Наивероятнейшее число успехов: Вычисляем np + p = 5∙1/2 + ½ = 3. Это Наивероятнейшее число успехов: Вычисляем np + p = 5∙1/2 + ½ = 3. Это целое число, поэтому m0 = np + p = 3 и m0' = np + p – 1 = 2. Самые большие (и равные между собой) вероятности у двух и трех появлений герба.

>Еще один пример Вероятность сдать экзамен равна 0,8. Найти наивероятнейшее число студентов, сдавших экзамен Еще один пример Вероятность сдать экзамен равна 0,8. Найти наивероятнейшее число студентов, сдавших экзамен в группе из 30 человек. Решение. Вычисляем np + p = 30∙0,8 + 0,8 = 24,8. Это не целое число, поэтому m0 = [24,8] = 24.

>Полиномиальная схема Определение Полиномиальной схемой называется последовательность n независимых одинаковых испытаний, в каждом из Полиномиальная схема Определение Полиномиальной схемой называется последовательность n независимых одинаковых испытаний, в каждом из которых возможны k исходов при этом вероятность любого исхода в каждом испытании постоянна,

>Полиномиальная формула Полиномиальная формула

>Пример Человек с вероятностью 0,2 оказывается брюнетом, с вероятностью 0,4 —шатеном, с вероятностью 0,3 Пример Человек с вероятностью 0,2 оказывается брюнетом, с вероятностью 0,4 —шатеном, с вероятностью 0,3 — блондином и с вероятностью 0,1—рыжим. Выбирается наугад группа из шести человек. Найти вероятность того, что в составе группы два брюнета, один шатен и три блондина.

>Гипергеометрические испытания Пусть из совокупности n предметов, среди которых n1 предметов первого вида и Гипергеометрические испытания Пусть из совокупности n предметов, среди которых n1 предметов первого вида и n2 предметов второго вида (n1 + n2 = n) производится выборка без возвращения m предметов, 1  m  n. Вероятность того, что в выборке будет m1 предметов первого вида и m2 предметов второго вида (m1 + m2 = m), согласно классическому определению вероятности, выражается формулой

>Гипергеометрические вероятности Данные испытания являются зависимыми. Гипергеометрические вероятности Данные испытания являются зависимыми.

>Пример В урне 6 белых и 5 черных шаров. Из урны вынимают наугад 5 Пример В урне 6 белых и 5 черных шаров. Из урны вынимают наугад 5 шаров. Найти вероятность, что два из них будут белыми, а три – черными. Решение:

>Предельные теоремы для схемы Бернулли При числе испытаний, превышающем 20, вычисление точного значения Pn(m) Предельные теоремы для схемы Бернулли При числе испытаний, превышающем 20, вычисление точного значения Pn(m) затруднительно. В этих случаях применяют приближенные формулы, вытекающие из предельных теорем. Различают два случая: когда р мало, используют приближение Пуассона, когда р не мало (и не очень близко к единице), справедливо приближение Муавра –Лапласа. Существует область, в которой возможно применение обоих приближений.

>Теорема Пуассона Если n  , р  0 так, что np  , Теорема Пуассона Если n  , р  0 так, что np  , 0 <  < , то для любого фиксированного mN справедливо:

>Приближенная формула Пуассона где  = np. Приближенную формулу Пуассона применяют при n > Приближенная формула Пуассона где  = np. Приближенную формулу Пуассона применяют при n > 30, р < 0.1, 0.1 <  = np < 10.

>Пример (дни рождения) Какова вероятность, что среди 500 случайно выбранных людей ни один не Пример (дни рождения) Какова вероятность, что среди 500 случайно выбранных людей ни один не родился 1 января ? Решение По формуле Бернулли

>По приближенной формуле Пуассона По приближенной формуле Пуассона

>Предельная теорема Муавра –Лапласа Если при n  и постоянном р, не равном 0 Предельная теорема Муавра –Лапласа Если при n  и постоянном р, не равном 0 или 1, величина ограничена так, что –  < а  хт  b < + , то

>Доказательство этой теоремы основано на применении формулы Стирлинга Доказательство этой теоремы основано на применении формулы Стирлинга

>Локальная приближенная формула Муавра –Лапласа Локальную приближенную формулу Муавра – Лапласа применяют при n Локальная приближенная формула Муавра –Лапласа Локальную приближенную формулу Муавра – Лапласа применяют при n > 30, 0.1  p  0.9, nрq > 9.

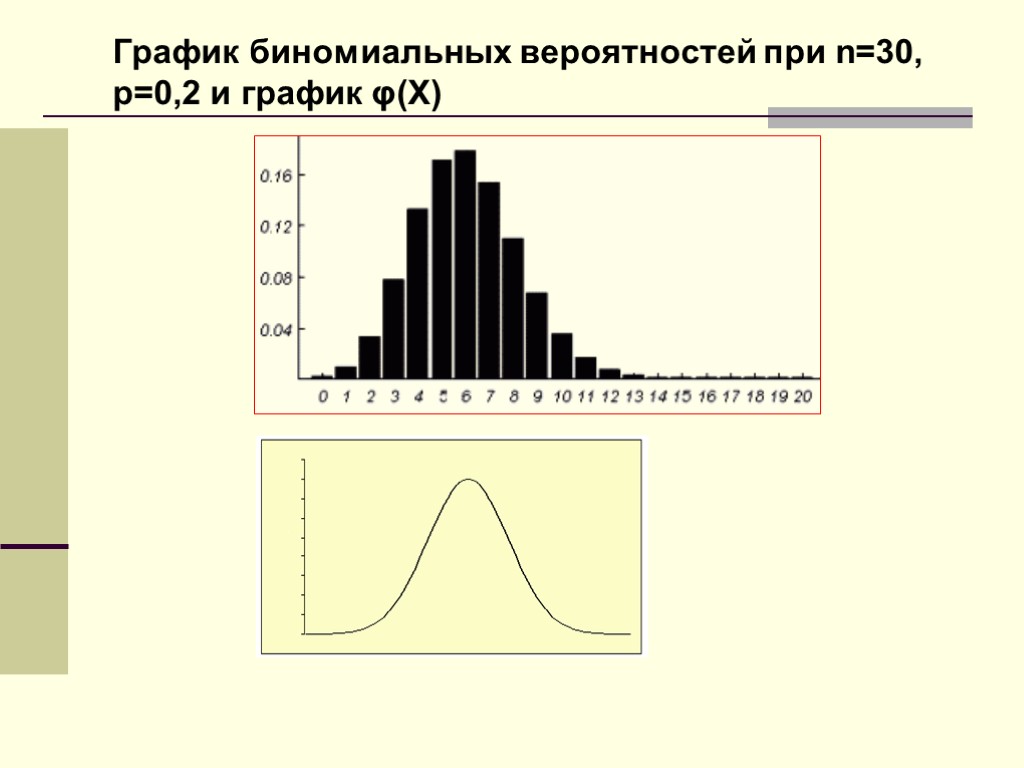
>График биномиальных вероятностей при n=30, p=0,2 и график φ(X) График биномиальных вероятностей при n=30, p=0,2 и график φ(X)

>Интегральная предельная теорема Муавра –Лапласа При n  и постоянном р, не равном 0 Интегральная предельная теорема Муавра –Лапласа При n  и постоянном р, не равном 0 или 1,

>Интегральная приближенная формула Муавра –Лапласа Интегральную приближенную формулу Муавра – Лапласа применяют при n Интегральная приближенная формула Муавра –Лапласа Интегральную приближенную формулу Муавра – Лапласа применяют при n > 30, 0.1  p  0.9, nрq > 9.

>Следствия Следствия

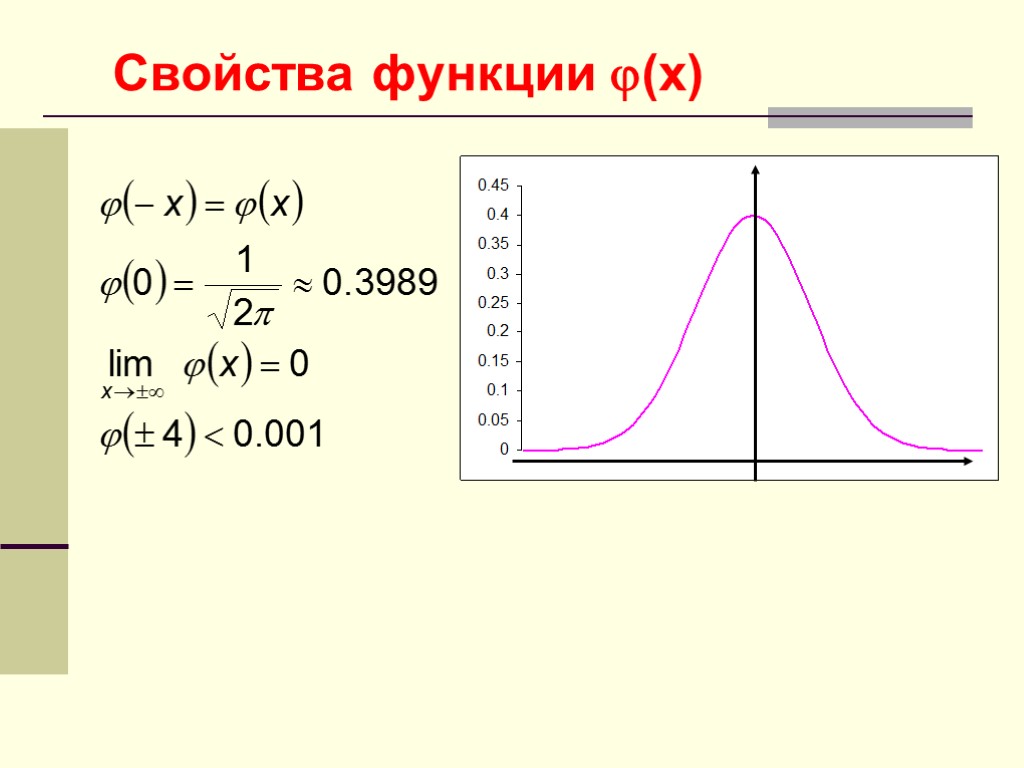
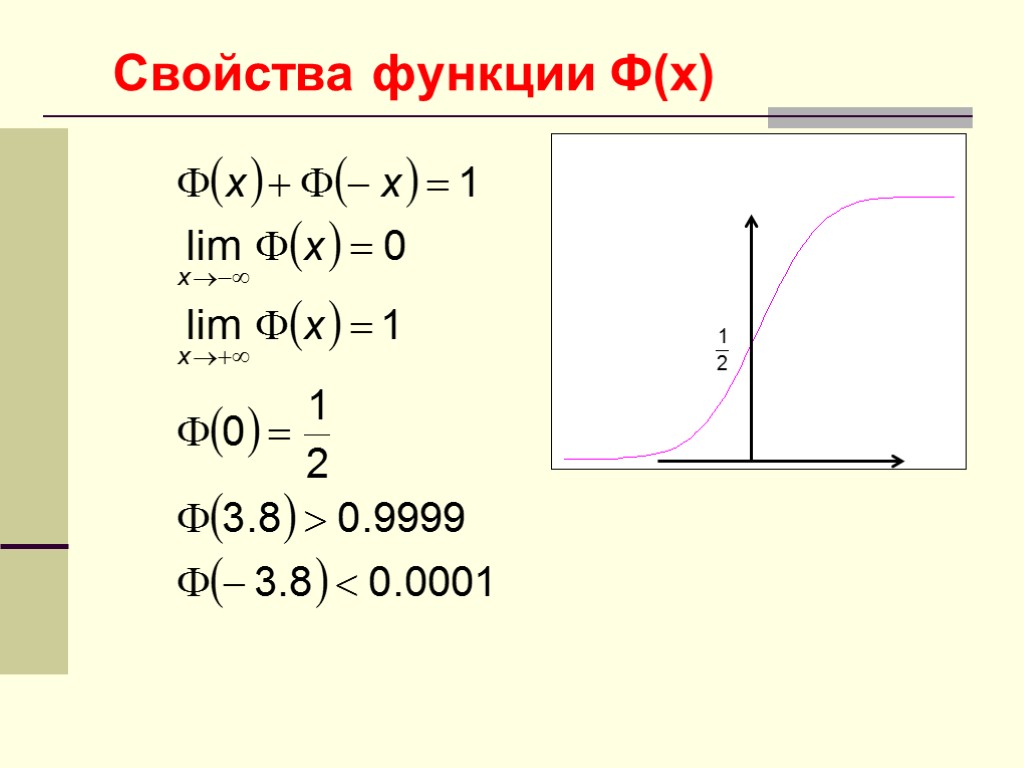
>Свойства функции (x) Свойства функции (x)

>Свойства функции Ф(x) Свойства функции Ф(x)

>Функция Лапласа Φ0(x). Вместо Φ(x) часто используют функцию Лапласа Φ0(x). Функция Лапласа Φ0(x). Вместо Φ(x) часто используют функцию Лапласа Φ0(x).

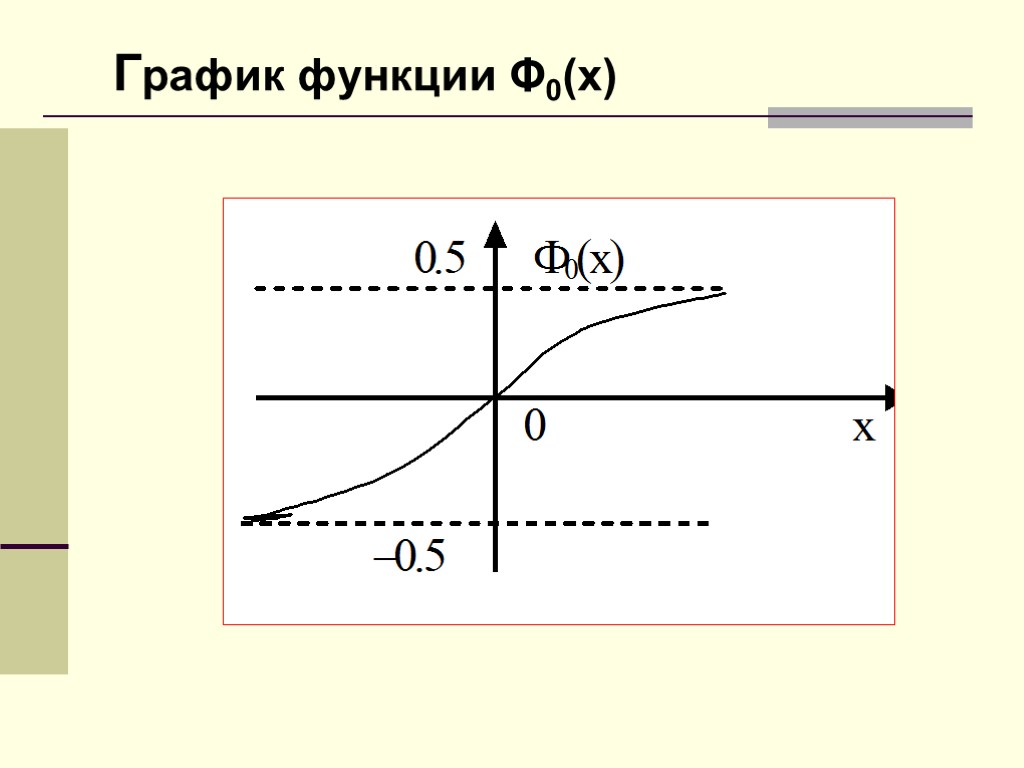
>График функции Φ0(x) График функции Φ0(x)

>Замечания поэтому в формулах может использоваться как Φ(x), так и Φ0(x). Значения функций находят Замечания поэтому в формулах может использоваться как Φ(x), так и Φ0(x). Значения функций находят в таблицах.

>Пример Вероятность рождения мальчика p = 0,5. Найти вероятность того, что в группе из Пример Вероятность рождения мальчика p = 0,5. Найти вероятность того, что в группе из 100 новорожденных мальчиков не меньше 60. Решение.