Теория принятия решений Часть 2 Принятие решений с

Теория принятия решений Часть 2. Принятие решений с помощью математических моделей Лекция 21: Детерминированные линейные модели с непрерывными переменными

Часть 1 Общая постановка задач и алгоритм их решения

Формальная постановка задачи

Линейное программирование Дж. Данциг. Целевая функция Симплекс

Основные постулаты линейного программирования Оптимальное решение всегда принадлежит одной из вершин симплекса. 2. Локально оптимальное решение задачи линейного программирования одновременно является и глобально оптимальным. 1.

Пример 1 Определить оптимальное решение задачи: где: хi – непрерывная неотрицательная переменная; Решение – симплекс методом.

Выделение базисных переменных. Пусть в качестве базисных (не равных нулю) переменных выбраны х1 и х5: x 1 = 8 + x 2 – 5 x 3 + x 4 – x 5. Отсюда: 5 х1 = 40 + 5 х2 – 25 х3 + 5 х4 – 5 х5 (2) Подставляя (2) в первое равенство системы (1), получим: 40 + 5 х2 – 25 х3 + 5 х4 – 5 х5 – 4 х2 + 13 х3 – 2 х4 + х5 = 20. Отсюда следует: х2 – 12 х3 + 3 х4 – 4 х5 + 20 = 0. Окончательное равенство, включающее х5, имеет вид: Подставляя (3) в выражение для х1, получим: После подстановки х1 и х5 в целевую функцию, получим:

Эквивалентная каноническая форма задачи (1) х1 и х5 – базисные переменные. Базисное решение: х1=3; x 5=5; x 2=x 3=x 4=0. Значение целевой функции = 28.

Переход к новому базису Т. к. коэффициент при х3 в целевой функции отрицателен, то увеличение х3 вызовет уменьшение функционала цели. Т. о. введению в базис подлежит х3. Теперь следует выбрать переменную, выводимую из базиса: х1 = 3 – 2 х3 из равенства (4) х5 = 5 - 3 х3 из равенства (5) то х Если : 5 станет <0, что недопустимо. то х1 станет <0, что недопустимо. из базиса выводится х1. Новый базис имеет вид: х3 = 1, 5; x 5 = 0, 5; x 1=x 2=x 4=0; f(x) = -8 Значение целевой функции уменьшилось с 28 до – 8. Новая система имеет вид: где х3 и х5 – базисные переменные.

Переход к новому базису Т. к. коэффициент при х2 в целевой функции отрицателен, в базис вводится х2. Для того, чтобы определить, какая переменная выводится из базиса, проанализируем выражения, получаемые из 1 -го и 2 го равенств:

Канонический вид системы с учетом нового базиса Поскольку все коэффициенты небазисных переменных положительны, полученное решение является глобально оптимальным:

Настройка пакета Simplexwin 3. 1 – ввод числа переменных и ограничений

Ввод исходных данных в пакет Simplexwin 3. 1

Вывод результатов пакетом Simplexwin 3. 1

Достоинства и недостатки симплекс-метода 1. Достоинства: Гарантия глобально оптимального решения. Высокое быстродействие независимо от размерности. Наличие большого числа программных реализаций. 2. Недостатки: Решаются только линейные задачи с непрерывными неотрицательными переменными.

Самостоятельно Решить задачу симплекс-методом, добавив переменные: S=5 x₁+8 x₂+3 x₃ max; 2 x₁+3 x₂+4 x₃ ≤ 12; x₁≥ 0; x₂ ≥ 0; x₃ ≥ 0.

Часть 2 Важный частный случай: задача с одним ограничением

Задача с одним видом ресурса Требуется определить вектор переменных Х, который бы максимизировал финансовые поступления на предприятие: (1) где: хi – объем выпускаемой продукции i-го вида (непрерывная неотрицательная переменная); сi – стоимость единицы выпускаемой продукции i-го вида; b – величина имеющегося ресурса (например, человекочасы); аi, – затраты единственного вида ресурса, приходящиеся на единицу i-го вида продукции.

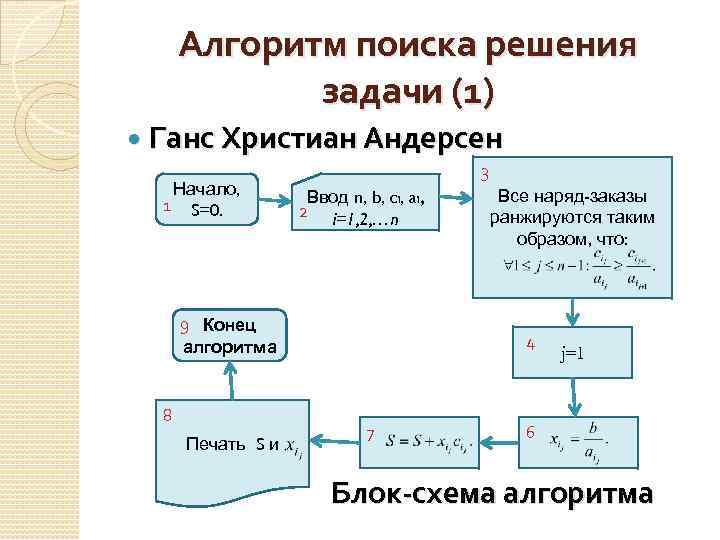Алгоритм поиска решения задачи (1) Ганс Христиан Андерсен Начало, 1 S=0. 3 Ввод n, b, ci, ai, 2 i=1, 2, …n 9 Конец алгоритма 8 Печать S и Все наряд-заказы ранжируются таким образом, что: 4 7 j=1 6 Блок-схема алгоритма

Достоинства и недостатки алгоритма 1. Достоинства: Гарантия глобально оптимального решения. Простота реализации. Высокое быстродействие. Низкие требования к ресурсам компьютера. 2. Недостаток: Узкий диапазон применения.

Пример 2 Решить самостоятельно, пользуясь приведенным выше алгоритмом и симплекс методом: S=5 x₁+9 x₂+3 x₃ max; 2 x₁+3 x₂+4 x₃ ≤ 12; x₁≥ 0; x₂ ≥ 0; x₃ ≥ 0. Ответ: x₁=0; x₂ =4; x₃ =0, S =36. max

Задача с одним видом ресурса и ограничениями на выпуск каждого вида продукции Требуется определить вектор переменных Х, который бы максимизировал финансовые поступления на предприятие: где: х – объем выпускаемой продукции i-го вида (непрерывная неотрицательная переменная); с – стоимость единицы выпускаемой i i продукции i-го вида; b – величина имеющегося ресурса (например, человекочасы); а – затраты единственного вида ресурса, приходящиеся на единицу i-го вида продукции, di - верхняя граница выпуска i-го вида продукции. i,

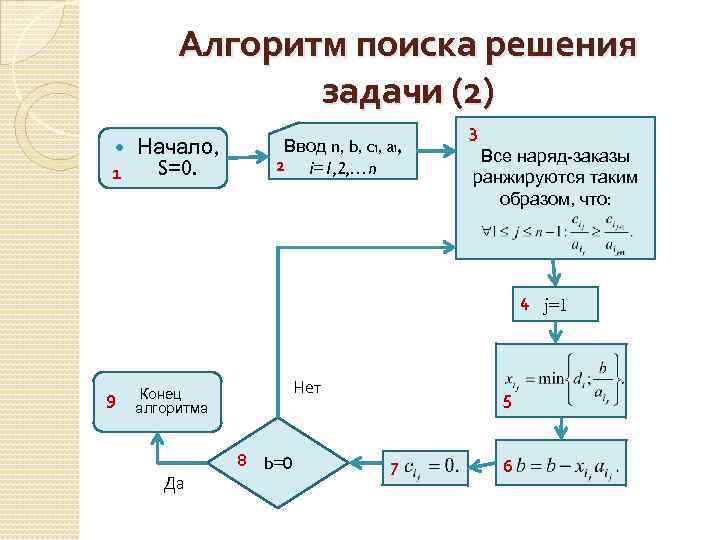Алгоритм поиска решения задачи (2) Начало, S=0. 1 Ввод n, b, ci, ai, 2 i=1, 2, …n 3 Все наряд-заказы ранжируются таким образом, что: 4 j=1 9 Нет Конец алгоритма Да 8 b=0 5 7 6

Достоинства и недостатки алгоритма 1. Достоинства: Гарантия глобально оптимального решения. Простота реализации. Высокое быстродействие. Низкие требования к ресурсам компьютера. 2. Недостаток: Узкий диапазон применения.

Пример 3 Решить самостоятельно, пользуясь приведенным выше алгоритмом и симплекс методом: S=5 x₁+9 x₂+3 x₃ max; 2 x₁+3 x₂+4 x₃ ≤ 12; 4≥x₁≥ 0; 2≥x₂ ≥ 0; 3≥x₃ ≥ 0. Ответ: x₁=3; x₂ =2; x₃=0; S=33.

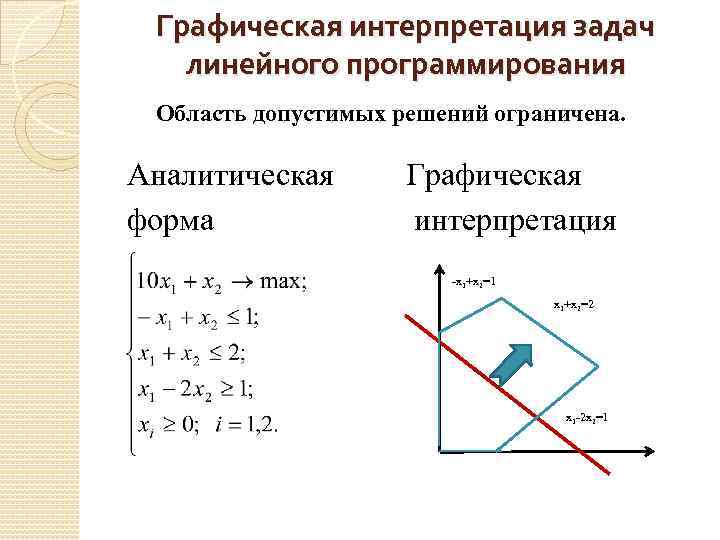Графическая интерпретация задач линейного программирования Область допустимых решений ограничена. Аналитическая Графическая форма интерпретация -x 1+x 2=1 x 1+x 2=2 x 1 -2 x 2=1

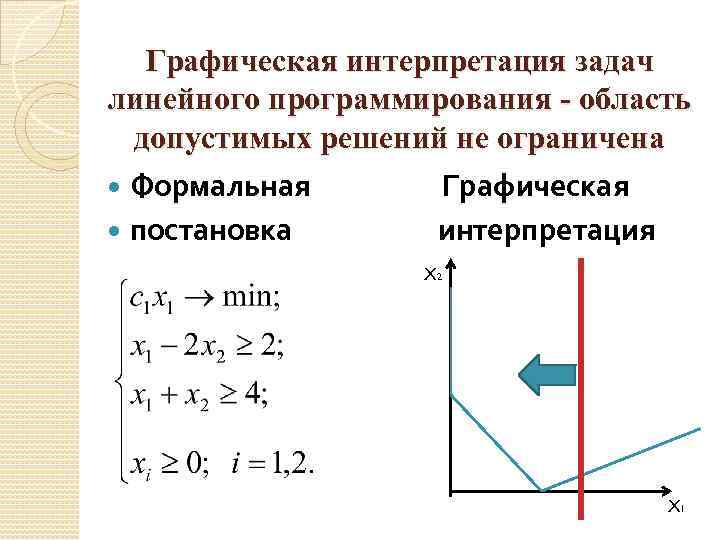Графическая интерпретация задач линейного программирования - область допустимых решений не ограничена Формальная Графическая постановка интерпретация X 2 X 1

Задачи ЛП на графах Задача о максимальном потоке: На графе G(X, U), множество вершин которого X, а множество дуг U, определить максимальный поток из вершины – источника в вершину – сток, если поток f (i, j) по дуге не может превысить пропускной способности дуги r(i, j).

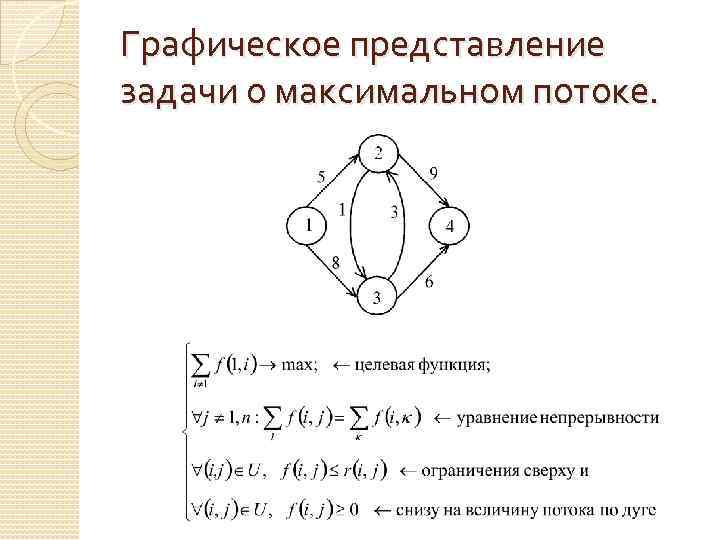Графическое представление задачи о максимальном потоке.

Задача о максимальной циркуляции на взвешенном орграфе Содержательная постановка задачи: на взвешенном орграфе с бикомпонентами требуется распределить замкнутые потоки (циркуляции) в контурах таким образом, чтобы: Их сумма в одной и той же дуге не превышала пропускной способности этой дуги. Суммарный вес всех циркуляций должен быть максимальным.

Формальная постановка задачи о максимальной циркуляции Здесь s(аi ) - циркуляция в i-о контуре; r(p, q) – пропускная способность дуги (p, q) множества U; A(p, q) – подмножество контуров, которым принадлежит дуга (p, q).

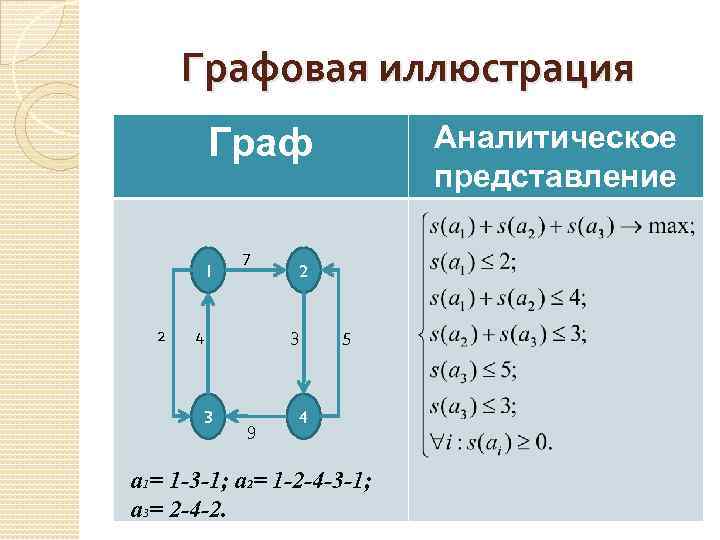Графовая иллюстрация Граф 1 7 2 2 4 3 5 3 9 4 a 1= 1 -3 -1; a 2= 1 -2 -4 -3 -1; a 3= 2 -4 -2. Аналитическое представление

Решение задачи программой поиска максимальных циркуляций на планарных графах

Прямые и двойственные задачи Прямая задача

Двойственная задача Общий вид: Двойственная к задаче (1)

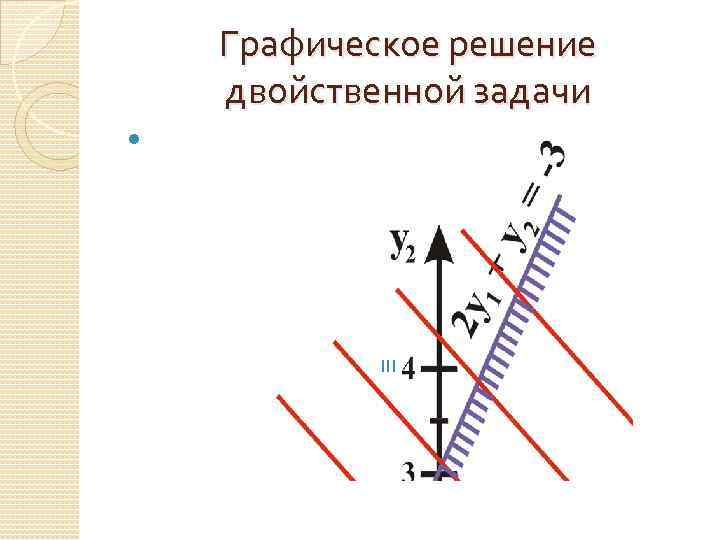Графическое решение двойственной задачи

Решить самостоятельно графически Задача № 1 Задача № 2