ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ Лінійні неперервні системи автоматичного керування

ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ «Лінійні неперервні системи автоматичного керування»

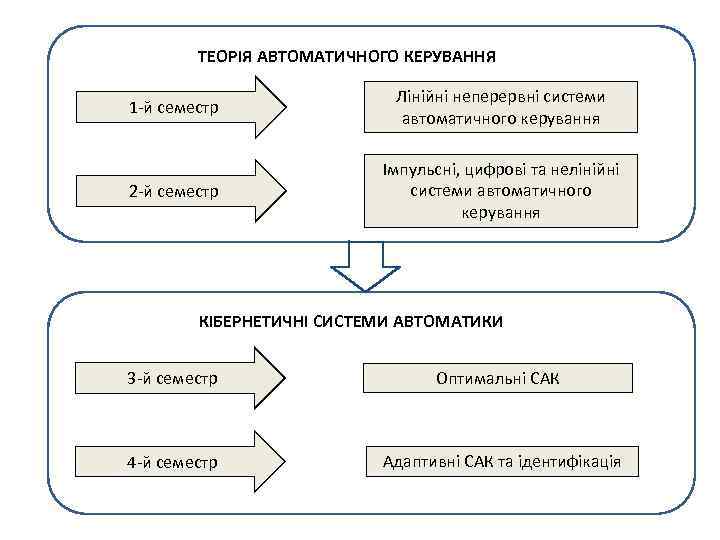ТЕОРІЯ АВТОМАТИЧНОГО КЕРУВАННЯ 1 -й семестр Лінійні неперервні системи автоматичного керування 2 -й семестр Імпульсні, цифрові та нелінійні системи автоматичного керування КІБЕРНЕТИЧНІ СИСТЕМИ АВТОМАТИКИ 3 -й семестр Оптимальні САК 4 -й семестр Адаптивні САК та ідентифікація

НАВЧАЛЬНИМ ПЛАНОМ ПЕРЕДБАЧЕНО Лекції: Практичні роботи: Лабораторні роботи: Наявність КР: Форма контролю знань: 36 годин 18 годин так іспит ЛІТЕРАТУРА 1. Попович М. Г. , Ковальчук О. В. Теорія автоматичного керування: Підручник. – 2 -ге вид. , перероб. і доп. – К. : Либідь, 2007. – 656 с. 2. Галай М. В. Теорія автоматичного керування: неперервні та дискретні системи: Навчальний посібник. – Полтава: ПНТУ, 2002. – 454 с. 3. Макаров И. М. Менский Б. М. Линейные автоматические системы. Учебное пособие для вузов. М. , 1977. – 464 с. 4. Бесекерский В. А. , Попов Е. П. Теория систем автоматического регулирования М. , 1966 г. , 992 с.

ПРЕДМЕТ І ЗАДАЧІ КУРСУ ТАК Метою вивчення курсу ТАК є: • освоєння принципів побудови різних типів систем автоматичного керування (САК); • вивчення властивостей і особливостей лінійних, нелінійних і дискретних САК; • вивчення методів аналізу стійкості та якості перехідних процесів; • вивчення методів синтезу корегувальних пристроїв з метою отримання заданих властивостей САК. ТАК дає методи вирішення задач двох типів: • задач аналізу роботи САК, коли за відомими характеристиками окремих елементів визначаються загальні характеристики системи і проводиться аналіз її робочого процесу; • задач синтезу, коли за вимогами, які пред'являються до системи, визначається структура САК і її окремі елементи. Іншими словами, вивчення курсу ТАК дозволяє навчитися: • розуміти, що таке САК, з яких елементів вона складається і які задачі вирішує; • аналізувати цю систему з точки зору стійкості її роботи та якості вирішення поставленої задачі; • корегувати САК за допомогою спеціальних пристроїв так, щоб вона відповідала висунутим вимогам.

ОСНОВНІ ПОНЯТТЯ І ВИЗНАЧЕННЯ Механізація – заміна праці людини в робочих операціях; Автоматизація – заміна праці людини в операціях керування; Автоматичні пристрої – це технічні пристрої, що виконують операції керування; Об'єкт керування (ОК) – це сукупність технічних засобів, що виконують процес і вимагають для цього спеціально організованих дій, наприклад, матеріальний об’єкт (електродвигун, автомобіль, ліфт, літак, приміщення) або процес (покраска, зборка машин, приготування суміші, опалення, вентиляція, кондиціонування повітря, очистка води тощо); Система керування – це сукупність засобів керування та об'єкта; Автоматична система – це система, в якій всі робочі операції та операції керування виконують автоматичні пристрої; Автоматизована система – це система, в якій автоматизована тільки частина операцій, а інша частина зберігається за людиною.

РІЗНОВИДИ САК Автоматичні системи можна класифікувати за багатьма ознаками: § за призначенням (системи керування технологічними режимами, апаратами і машинами); § за характером керованих величин (системи регулювання температури, густини середовища, тиску та ін. ); § за видом енергії, що використовується для керування (електричні, гідравлічні, пневматичні й ін. ). За характером зміни задавального впливу: § системи стабілізації; § системи програмного управління; § слідкуючі системи. Лінійні автоматичні системи - це такі системи, які можна описати з достатньою точністю лінійними рівняннями (алгебраїчними, диференціальними, рівняннями в кінцевих різницях і т. д. Лінійні системи поділяють на стаціонарні і нестаціонарні. Нелінійні системи - автоматичні системи, динаміка яких описується нелінійними рівняннями.

Алгоритмічна (функціональна) схема найпростішої системи автоматичного керування (розімкнене керування): x(t) – задавальна дія (вхідна величина); u(t) – керуюча дія, за допомогою якого виконується безпосереднє керування; y(t) – вихідна координата (величина), яка характеризує стан об'єкта; f(t) – збурення, яке заважає нормальному перебігу процесу керування.

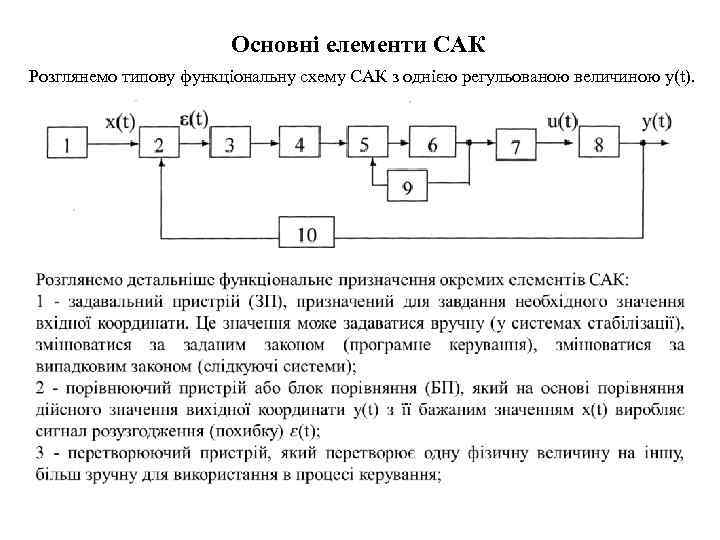Основні елементи САК Розглянемо типову функціональну схему САК з однією регульованою величиною y(t).

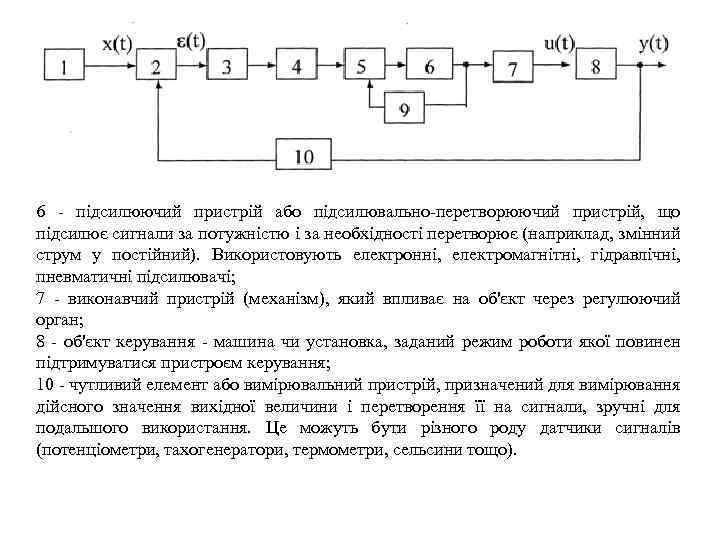6 - підсилюючий пристрій або підсилювально-перетворюючий пристрій, що підсилює сигнали за потужністю і за необхідності перетворює (наприклад, змінний струм у постійний). Використовують електронні, електромагнітні, гідравлічні, пневматичні підсилювачі; 7 - виконавчий пристрій (механізм), який впливає на об'єкт через регулюючий орган; 8 - об'єкт керування - машина чи установка, заданий режим роботи якої повинен підтримуватися пристроєм керування; 10 - чутливий елемент або вимірювальний пристрій, призначений для вимірювання дійсного значення вихідної величини і перетворення її на сигнали, зручні для подальшого використання. Це можуть бути різного роду датчики сигналів (потенціометри, тахогенератори, термометри, сельсини тощо).

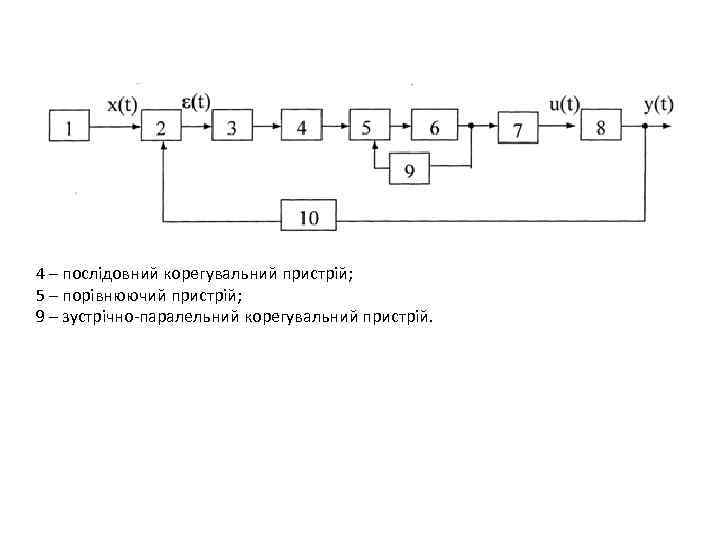4 – послідовний корегувальний пристрій; 5 – порівнюючий пристрій; 9 – зустрічно-паралельний корегувальний пристрій.

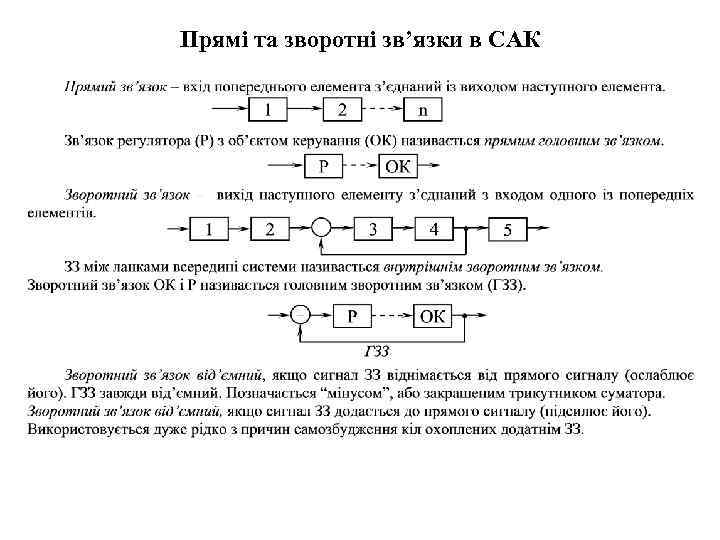Прямі та зворотні зв’язки в САК

Лекція № 2 ПРИНЦИПИ ТА ОСНОВНІ ВИДИ КЕРУВАННЯ

Принцип розімкнутого керування Суть принципу полягає в тому, що алгоритм керування виробляється тільки на основі заданого алгоритму функціонування і в процесі роботи система ніяк не коректується. У цьому випадку керуючий вплив u(t) формується шляхом функціонального перетворення задавального впливу x(t) з урахуванням характеристик ОК, тобто алгоритм керування може бути записаний у вигляді: u =f(x). Схема має вид розімкнутого кола, що й визначило назву принципу. Недоліки: такі системи не забезпечують точності за наявності завад і зміни параметрів об'єкта. Переваги: простота конструкції, висока швидкодія, мала споживана енергія.

ПРИНЦИП КОМПЕНСАЦІЇ (керування за збуренням, принцип Понселе) Якщо збурюючий вплив великий і розімкнута САК не забезпечує потрібної точності, то іноді можна, вимірявши збурення, внести корективи в алгоритм керування, які компенсували б відхилення алгоритму функціонування. Ступінь компенсації залежить від точності знання характеристик об'єкта і точності виміру збурення. Недоліки: цей принцип можна використовувати тільки в тих випадках, коли відомі характеристики об'єкта і можливе вимірювання збурюючого впливу. Переваги: даний принцип є найшвидшим принципом регулювання, має високу стійкість.

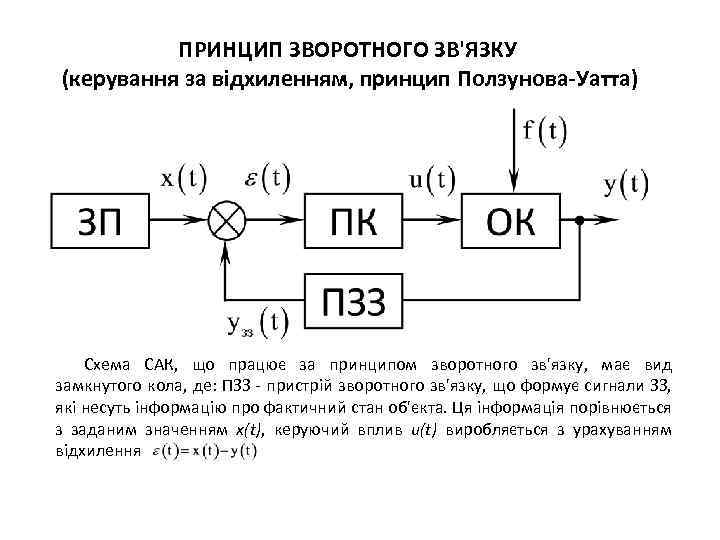ПРИНЦИП ЗВОРОТНОГО ЗВ'ЯЗКУ (керування за відхиленням, принцип Ползунова-Уатта) Схема САК, що працює за принципом зворотного зв'язку, має вид замкнутого кола, де: ПЗЗ - пристрій зворотного зв'язку, що формує сигнали ЗЗ, які несуть інформацію про фактичний стан об'єкта. Ця інформація порівнюється з заданим значенням х(t), керуючий вплив u(t) виробляється з урахуванням відхилення

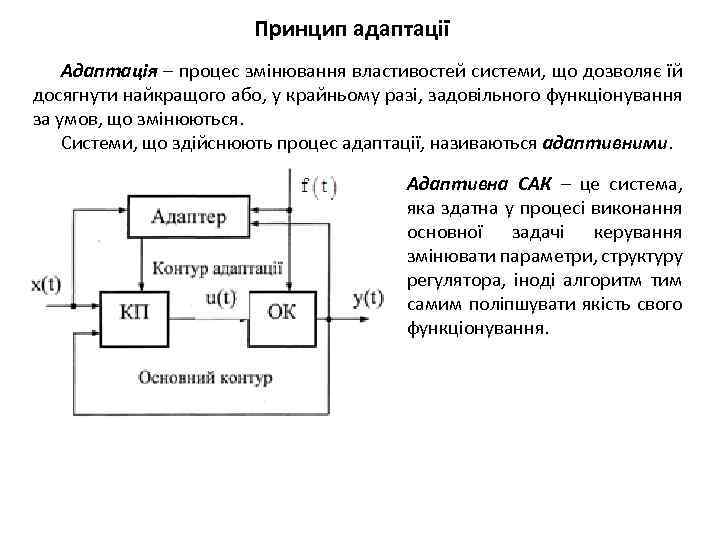Принцип адаптації Адаптація – процес змінювання властивостей системи, що дозволяє їй досягнути найкращого або, у крайньому разі, задовільного функціонування за умов, що змінюються. Системи, що здійснюють процес адаптації, називаються адаптивними. Адаптивна САК – це система, яка здатна у процесі виконання основної задачі керування змінювати параметри, структуру регулятора, іноді алгоритм тим самим поліпшувати якість свого функціонування.

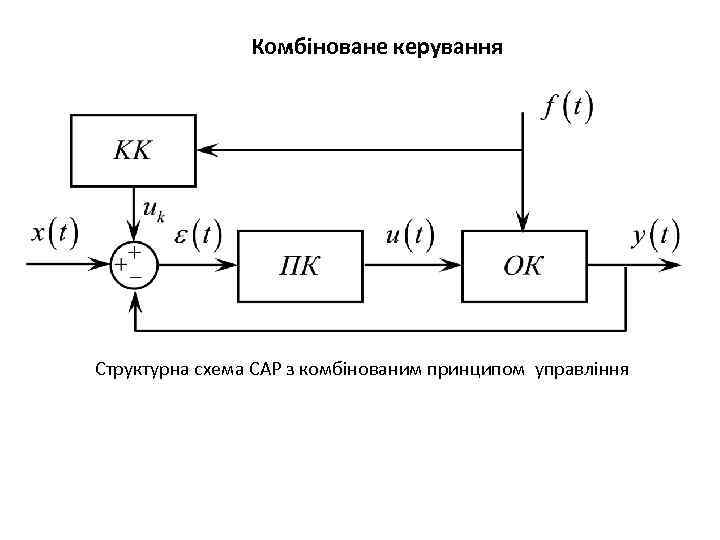Комбіноване керування Структурна схема САР з комбінованим принципом управління

Основні види автоматичного керування Основними задачами автоматичного керування є: 1) підтримання величини вихідної координати постійною; 2) зміна вихідної координати за заданою програмою; 3) зміна вихідної координати за деяким випадковим законом, апріорно невідомим. Відповідно до цих задач можна виділити такі групи САК: 1) системи стабілізації; 2) системи програмного керування; 3) слідкуючі системи; 4) системи екстремального керування; 5) оптимальні системи; 6) адаптивні системи.

Лекція № 3 «РЕЖИМИ РОБОТИ САК, ЗАКОНИ КЕРУВАННЯ, ТЕСТОВІ СИГНАЛИ»

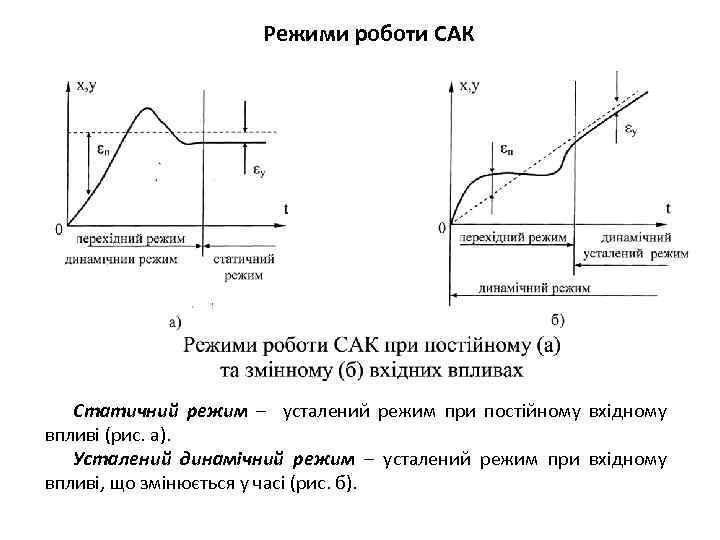Режими роботи САК Статичний режим – усталений режим при постійному вхідному впливі (рис. а). Усталений динамічний режим – усталений режим при вхідному впливі, що змінюється у часі (рис. б).

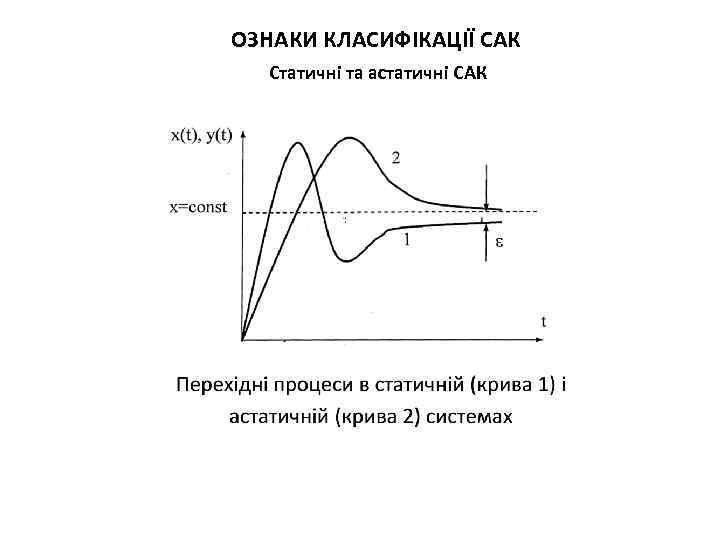ОЗНАКИ КЛАСИФІКАЦІЇ САК Статичні та астатичні САК

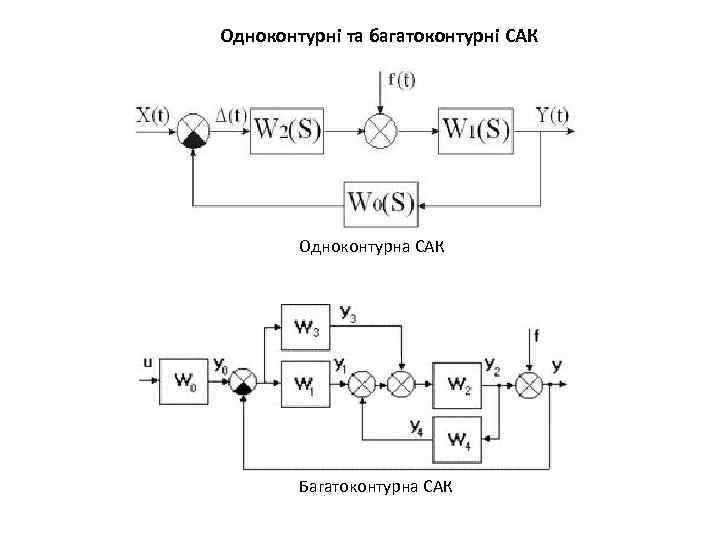Одноконтурні та багатоконтурні САК Одноконтурна САК Багатоконтурна САК

ОСНОВНІ ЗАКОНИ РЕГУЛЮВАННЯ Законом регулювання називають математичну залежність, відповідно до якої керуючий пристрій (Р), виробляє керуючій вплив . Пропорційний закон (П): керуючий сигнал пропорційний відхиленню Інтегральний закон (І): керуючий сигнал пропорційний інтегралу похибки де Ті – стала часу інтегрування.

Пропорційно-інтегральний закон (ПІ): керуючий сигнал має вигляд: тобто регулювання відбувається за відхиленням і за інтегралом цього відхилення (похибки). Пропорційно-інтегрально-диференціальний закон (ПІД): керуючий сигнал записується у вигляді: керуюча дія пропорційна похибці, інтегралу від похибки і похідної від неї. де Тд - стала часу диференціювання.

Сигнали, що використовуються при аналізі САК. Часові характеристики. Одинична ступінчаста дія (функція Хевісайда). Ця дія має вигляд одиничного стрибка. Її називають також одиничною функцією l(t), яка набуває таких значень: Одиничний імпульс (δ-функція, функція Дірака). Ця дія являє собою дуже вузький імпульс, що обмежує одиничну площу. Тобто δ-функція задовольняє умовам:

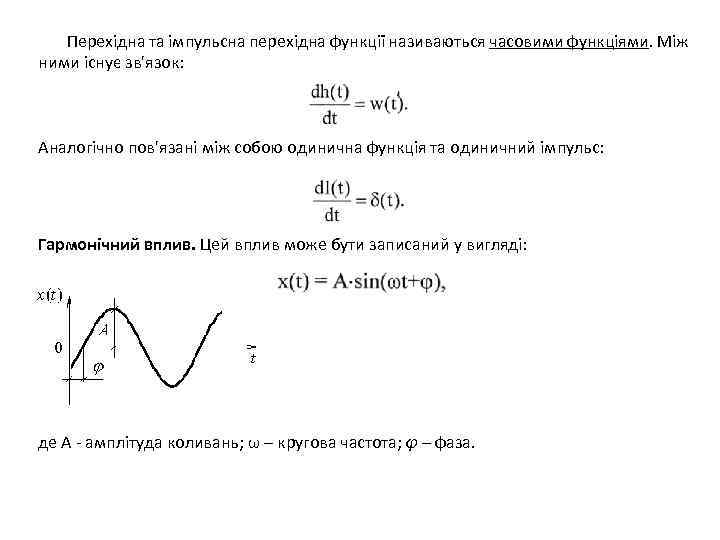Перехідна та імпульсна перехідна функції називаються часовими функціями. Між ними існує зв'язок: Аналогічно пов'язані між собою одинична функція та одиничний імпульс: Гармонічний вплив. Цей вплив може бути записаний у вигляді: де А - амплітуда коливань; ω – кругова частота; φ – фаза.

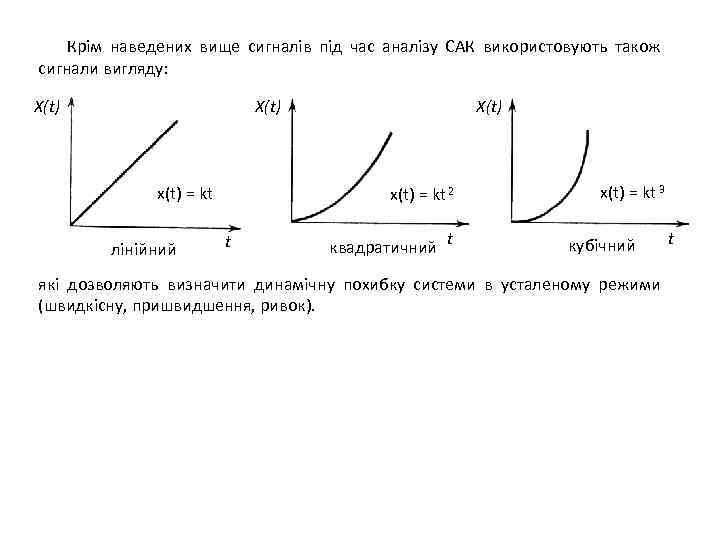Крім наведених вище сигналів під час аналізу САК використовують також сигнали вигляду: X(t) x(t) = kt лінійний X(t) x(t) = kt 2 t квадратичний t x(t) = kt 3 кубічний в) які дозволяють визначити динамічну похибку системи в усталеному режими (швидкісну, пришвидшення, ривок). t

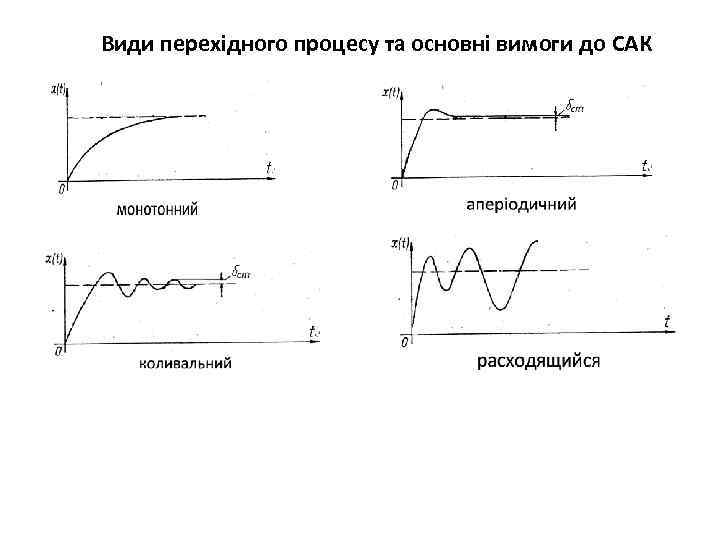Види перехідного процесу та основні вимоги до САК

Лекція № 4 «МАТЕМАТИЧНИЙ ОПИС САК»

Математичні моделі САК. Рівняння динаміки і статики У більшості випадків безперервні САК описуються нелінійними диференціальними рівняннями n-го порядку, які можуть бути записані у вигляді: Якщо припустити, що вплив x(t) не змінюється і має постійне значення х0, а процес у системі усталився, і вихідна координата набула значення у0, то рівняння набуде вигляду: Статичною характеристикою називається залежність вихідної величини від вхідної в усталеному режимі.

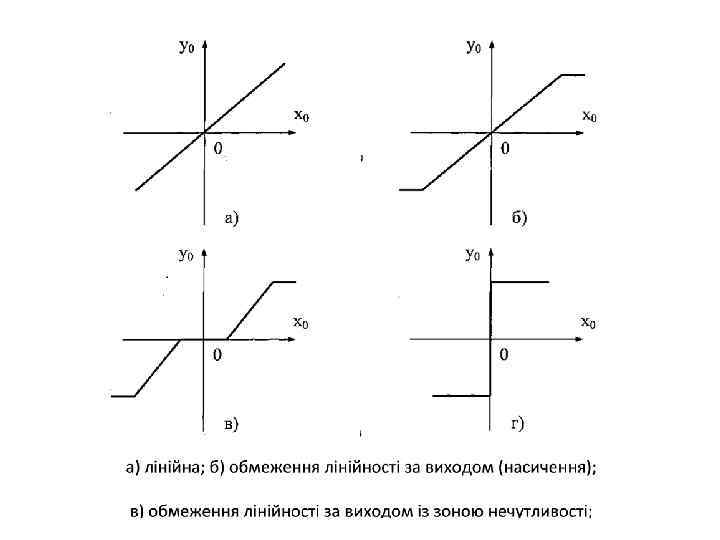
У результаті лінеаризації математична модель САК зводиться до системи лінійних диференціальних рівнянь чи до одного лінійного диференціального рівняння n-го порядку: (1) де y(t) – вихідна величина елемента або системи; x(t)– вхідна величина елемента або системи; aj, bj– коефіцієнти, які залежать від конструктивних параметрі елемента або елементів системи. З метою скорочення запису, вводять оператор диференціювання (2) і виносять за дужки вихідну і вхідну величини, диференційне рівняння в операторній формі набуває вигляду: (3)

Представивши вираз в дужках як многочлен від р, диференціальне рівняння можна скорочено записати в наступному вигляді: (4) де (5) (6) Вираз (5) називається вихідним оператором елемента або системи, а (6) – вхідним оператором. Передаточна функція Передаточною функцією в операторній формі називається відношення оператора впливу до власного оператора: Тоді рівняння системи може бути записано в більш компактній формі:

Перетворення Лапласа Перетворенням Лапласа називають співвідношення: Це співвідношення ставить у відповідність функції x(t) дійсної змінної t функцію X(s) комплексної змінної При цьому x(t) називають оригіналом, a X(s) - зображенням за Лапласом. Це записують таким чином: , або . Cимволічний запис: , де L - оператор Лапласа. Співвідношення визначає за відомим зображенням його оригінал і називається оберненим перетворенням Лапласа. Символічно це можна записати так: де – обернений оператор Лапласа.

Рівняння (3) може бути записано також в операційній формі, якщо до лівої та правої частин застосувати перетворення Лапласа: (7) Введемо поняття передавальної функції за Лапласом. Передавальною функцією за Лапласом W(s) називається відношення зображення вихідної величини до зображення вхідної величини за нульових початкових умов. Із (7) отримуємо: (8) Тоді рівняння можна записати у вигляді Y(s) = W(s)*X(s). (9) Знаменник передавальної функції (8) є характеристичним поліномом системи. Якщо його прирівняти до нуля, отримаємо характеристичне рівняння САК, тобто

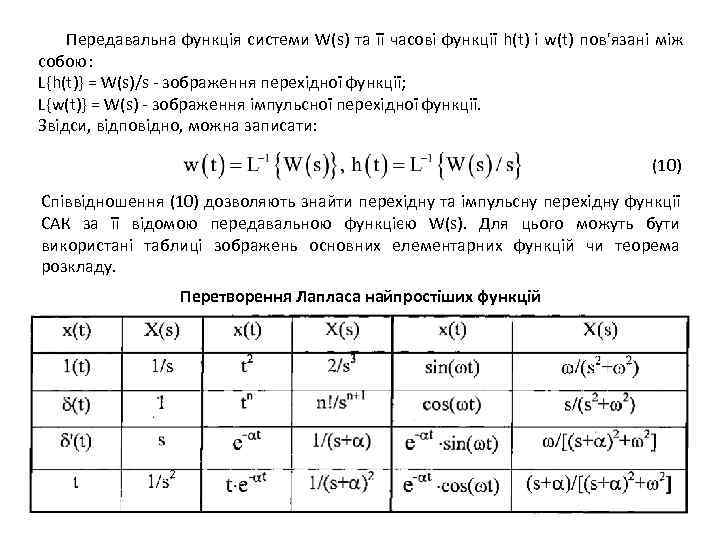Передавальна функція системи W(s) та її часові функції h(t) і w(t) пов'язані між собою: L{h(t)} = W(s)/s - зображення перехідної функції; L{w(t)} = W(s) - зображення імпульсної перехідної функції. Звідси, відповідно, можна записати: (10) Співвідношення (10) дозволяють знайти перехідну та імпульсну перехідну функції САК за її відомою передавальною функцією W(s). Для цього можуть бути використані таблиці зображень основних елементарних функцій чи теорема розкладу. Перетворення Лапласа найпростіших функцій

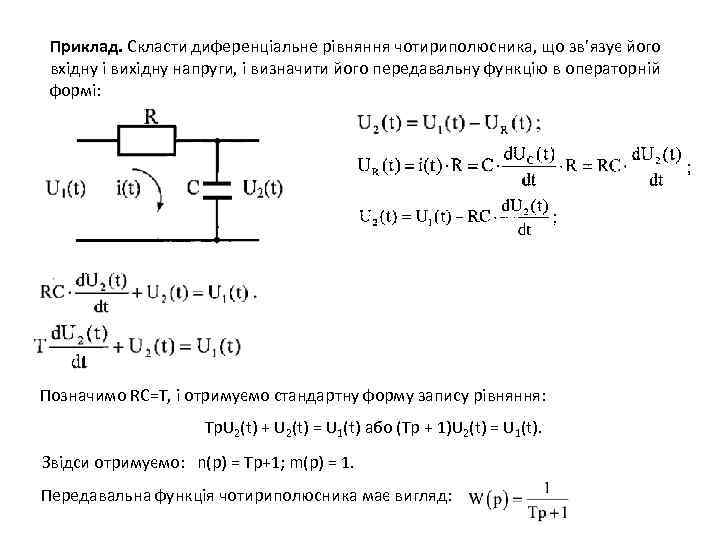Приклад. Скласти диференціальне рівняння чотириполюсника, що зв’язує його вхідну і вихідну напруги, і визначити його передавальну функцію в операторній формі: Позначимо RC=T, і отримуємо стандартну форму запису рівняння: Tp. U 2(t) + U 2(t) = U 1(t) або (Тр + 1)U 2(t) = U 1(t). Звідси отримуємо: n(p) = Тр+1; m(p) = 1. Передавальна функція чотириполюсника має вигляд:

Лекція № 6 Типові динамічні ланки та їх характеристики

Типовою динамічною ланкою називається елемент системи, передавальна функція якого має вигляд простого множника чи простого дробу.

ПРОПОРЦІЙНА ЛАНКА Пропорційною (підсилювальною, безінерційною, ідеальною) називається ланка, яка описується рівнянням: де k - коефіцієнт пропорційності (підсилення). Використовуючи властивості перетворення Лапласа, запишемо операційне рівняння: Звідси передавальна функція ланки за Лапласом: W(s) = Y(s)/X(s) = k. КПФ та частотні функції ланки мають вигляд:

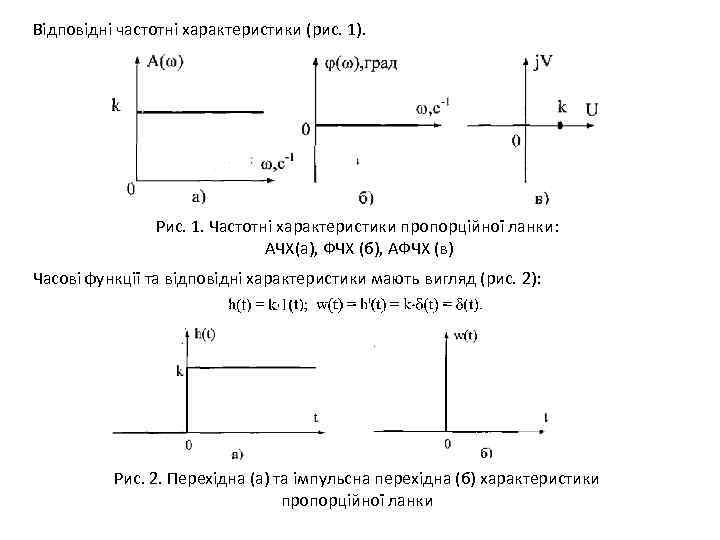Відповідні частотні характеристики (рис. 1). Рис. 1. Частотні характеристики пропорційної ланки: АЧХ(а), ФЧХ (б), АФЧХ (в) Часові функції та відповідні характеристики мають вигляд (рис. 2): Рис. 2. Перехідна (а) та імпульсна перехідна (б) характеристики пропорційної ланки

ДИФЕРЕНЦІАЛЬНА ЛАНКА Диференціальною називається ланка, яка описується рівнянням: тобто вихідний сигнал пропорційний швидкості зміни вхідного сигналу. Операційне рівняння та передавальна функція ланки: Частотні функції мають вигляд: Рис. 3. Частотні характеристики диференціальної ланки: АЧХ(а), ФЧХ (б), АФЧХ (в)

Часові функції та характеристики диференціальної ланки (рис. 4): Рис. 4. Перехідна (а) та імпульсна перехідна (б) характеристики диференціальної ланки Реальні диференціальні ланки є інерційними і тому описуються передавальними функціями вигляду: де Т - стала часу, що враховує інерційні властивості реальної диференціальної ланки. Чим менше значення Т, тим ближче властивості реальної ланки до властивостей ідеальної диференціальної ланки.

ІНТЕГРУЮЧА ЛАНКА Інтегруючою називається ланка, яка описується рівнянням: Операційне рівняння і передавальна функція ланки: КПФ та частотні функції мають вигляд: Логарифмічна амплітудна частотна характеристика ланки: тобто ЛАЧХ являє собою пряму, що проходить через точку з координатами та має нахил -20 д. Б/дек. Вона перетинає вісь частот при (рис. 5 г).

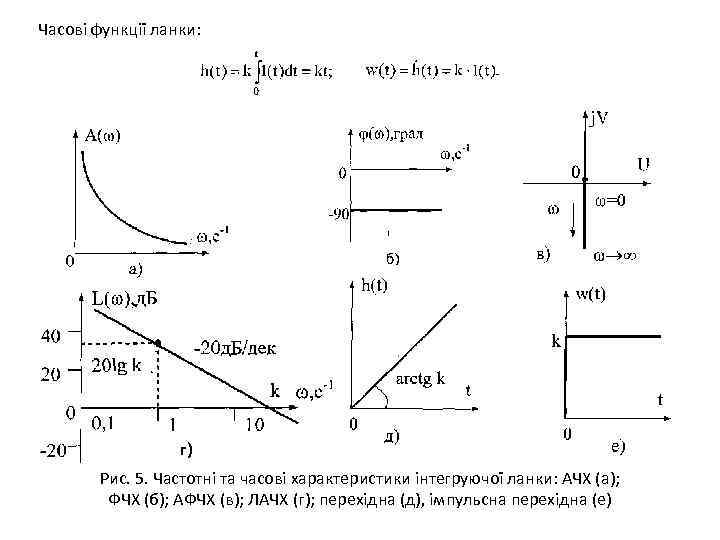Часові функції ланки: г) Рис. 5. Частотні та часові характеристики інтегруючої ланки: АЧХ (а); ФЧХ (б); АФЧХ (в); ЛАЧХ (г); перехідна (д), імпульсна перехідна (е)

Реальні елементи систем керування є інерційними, тому передавальна функція реального інтегратора має вигляд: де Т - стала часу, що враховує інерційні властивості реальної інтегруючої ланки. АПЕРІОДИЧНА ЛАНКА Аперіодичною, називається ланка, яка описується рівнянням першого порядку: Операційне рівняння має вигляд: звідси передавальна функція ланки: Частотні функції ланки мають вигляд:

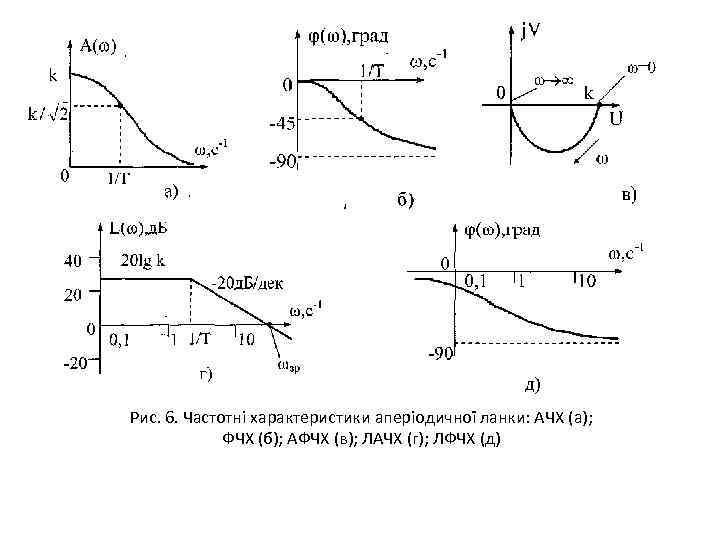Рис. 6. Частотні характеристики аперіодичної ланки: АЧХ (а); ФЧХ (б); АФЧХ (в); ЛАЧХ (г); ЛФЧХ (д)

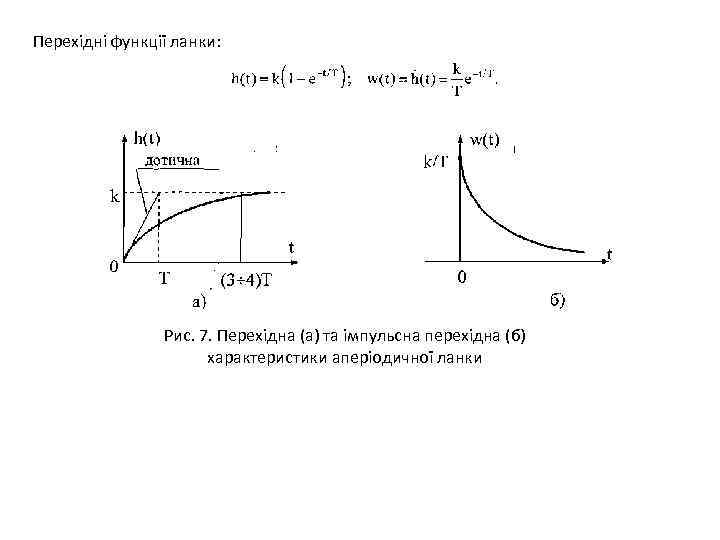Перехідні функції ланки: Рис. 7. Перехідна (а) та імпульсна перехідна (б) характеристики аперіодичної ланки

КОЛИВАЛЬНА ЛАНКА. Коливальною називається ланка, яка описується рівнянням другого порядку (1) де (ксі) – коефіцієнт затхання або демпфування Операційне рівняння: Передавальна функція ланки: Частотні функції мають вигляд: При амплітуда , тобто для різних значень коефіцієнта затухання на частоті , яку називають резонансною, амплітуда набуває значень від k/2 до (рис. 8, а: ).

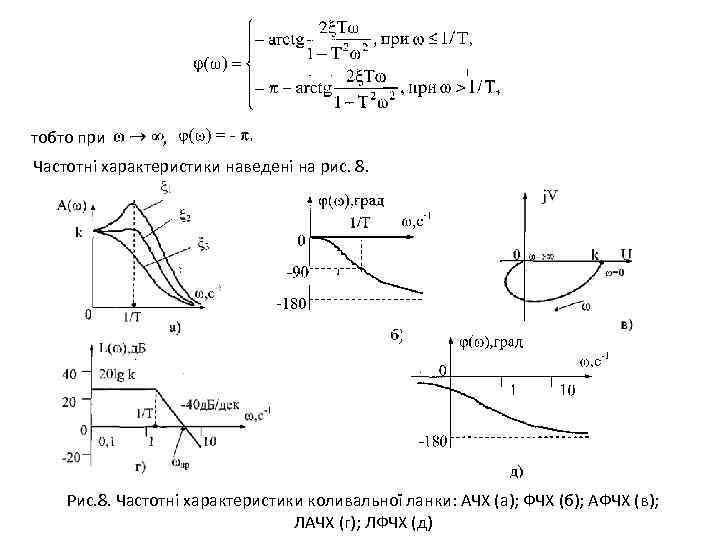тобто при , Частотні характеристики наведені на рис. 8. Рис. 8. Частотні характеристики коливальної ланки: АЧХ (а); ФЧХ (б); АФЧХ (в); ЛАЧХ (г); ЛФЧХ (д)

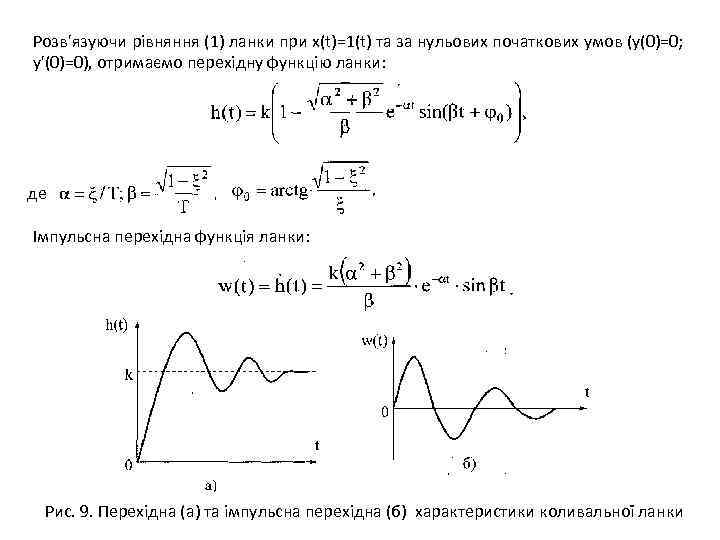Розв'язуючи рівняння (1) ланки при x(t)=1(t) та за нульових початкових умов (у(0)=0; у'(0)=0), отримаємо перехідну функцію ланки: де , Імпульсна перехідна функція ланки: Рис. 9. Перехідна (а) та імпульсна перехідна (б) характеристики коливальної ланки

КОНСЕРВАТИВНА ЛАНКА Якщо опір каналу обміну енергії дорівнює нулю, тобто (не втрачається енергія), то коливальна ланка вироджується в консервативну (резонансну) ланку, рівняння якої має вигляд: (2) Цьому рівнянню відповідає передавальна функція Частотні функції ланки: ; ; ; . Із цих виразів видно, що АЧХ на частоті має розрив, а ФЧХ - східчасто змінює своє значення з 0 на (рис. 10)

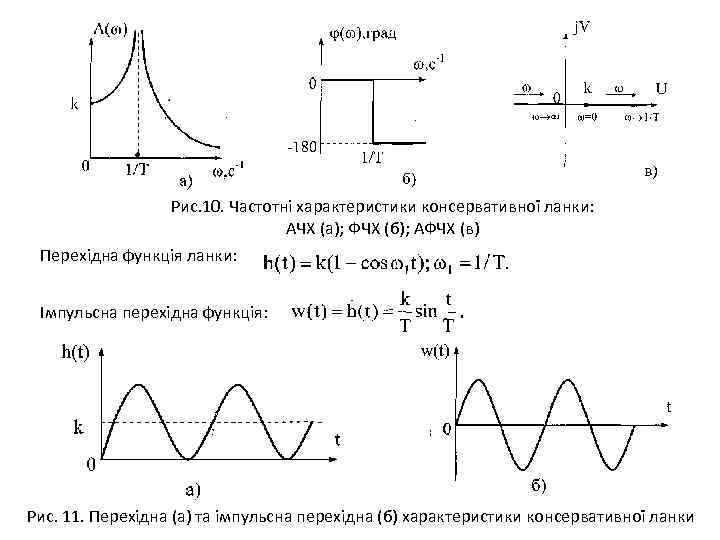Рис. 10. Частотні характеристики консервативної ланки: АЧХ (а); ФЧХ (б); АФЧХ (в) Перехідна функція ланки: Імпульсна перехідна функція: Рис. 11. Перехідна (а) та імпульсна перехідна (б) характеристики консервативної ланки

АПЕРІОДИЧНА ЛАНКА ДРУГОГО ПОРЯДКУ Якщо коефіцієнт затухання , то передавальну функцію коливальної ланки можна привести до вигляду: (3) де Цю ланку можна уявити як послідовне з'єднання двох аперіодичних ланок першого порядку, тому вона не належить до числа елементарних ланок. ФОРСУЮЧА ЛАНКА Форсуючою називається ланка, яка описується рівнянням: (4) Операційне рівняння і передавальна функція: Частотні функції:

Рис. 12. Частотні характеристики форсуючої ланки: АЧХ (а); ФЧХ (б); АФЧХ (в); ЛАЧХ (г) Часові функції форсуючої ланки: ФОРСУЮЧА ЛАНКА ДРУГОГО ПОРЯДКУ Ланка описується рівнянням: (5) і має передавальну функцію:

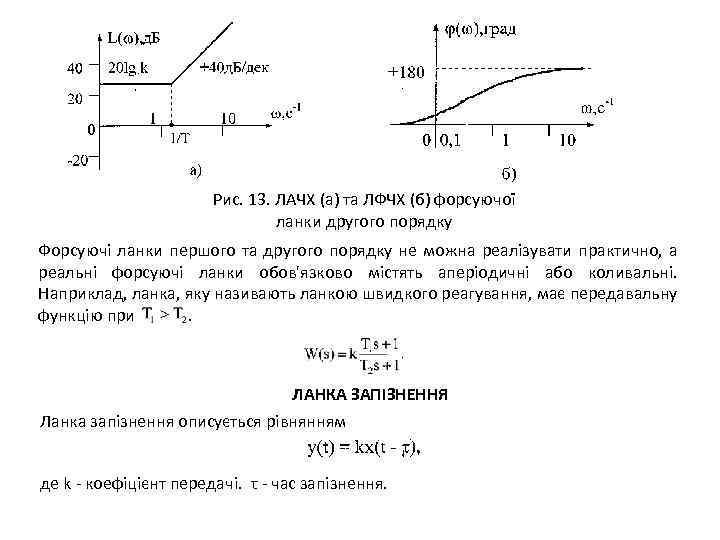Рис. 13. ЛАЧХ (а) та ЛФЧХ (б) форсуючої ланки другого порядку Форсуючі ланки першого та другого порядку не можна реалізувати практично, а реальні форсуючі ланки обов'язково містять аперіодичні або коливальні. Наприклад, ланка, яку називають ланкою швидкого реагування, має передавальну функцію при . ЛАНКА ЗАПІЗНЕННЯ Ланка запізнення описується рівнянням де k - коефіцієнт передачі. τ - час запізнення.

Передавальна функція ланки: Частотні функції ланки: Часові функції мають вигляд: Рис. 14. Характеристики ланки запізнення: АЧХ (а); ФЧХ (б); АФЧХ (в); перехідна (г); імпульсна перехідна (д)

МІНІМАЛЬНО ФАЗОВІ ЛАНКИ Мінімально фазовою є ланка, в якої всі нулі чисельника передаточної функції та полюси знаменника мають від’ємні або рівні нулю дійсні частини. Полюсами передаточної функції э значення, при яких передаточна функція має значення, рівне нескінченності. Такі значення вона має, коли знаменних дорівнює нулю. Тобто корені знаменника передаточної функції називаються її полюсами. НЕМІНІМАЛЬНО-ФАЗОВІ ЛАНКИ Ланка називається немінімально-фазовою, якщо хоча б один нуль чи полюс її передавальної функції має додатну дійсну частину (рівняння мають від'ємні коефіцієнти). Немінімально-фазові ланки, що мають полюси з додатною дійсною частиною називають нестійкими. Прикладами нестійких немінімально-фазових елементарних ланок є ланки з передавальними функціями: Стійкі немінімально-фазові ланки мають нулі з додатною дійсною частиною:

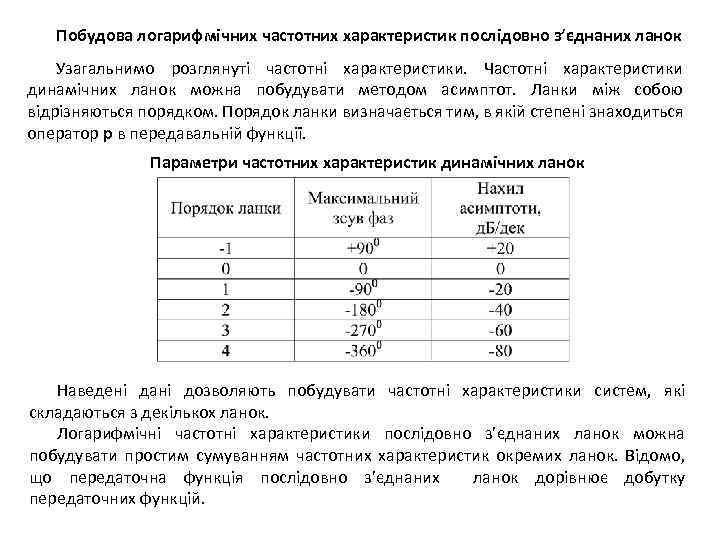Побудова логарифмічних частотних характеристик послідовно з’єднаних ланок Узагальнимо розглянуті частотні характеристики. Частотні характеристики динамічних ланок можна побудувати методом асимптот. Ланки між собою відрізняються порядком. Порядок ланки визначається тим, в якій степені знаходиться оператор р в передавальній функції. Параметри частотних характеристик динамічних ланок Наведені дані дозволяють побудувати частотні характеристики систем, які складаються з декількох ланок. Логарифмічні частотні характеристики послідовно з’єднаних ланок можна побудувати простим сумуванням частотних характеристик окремих ланок. Відомо, що передаточна функція послідовно з’єднаних ланок дорівнює добутку передаточних функцій.

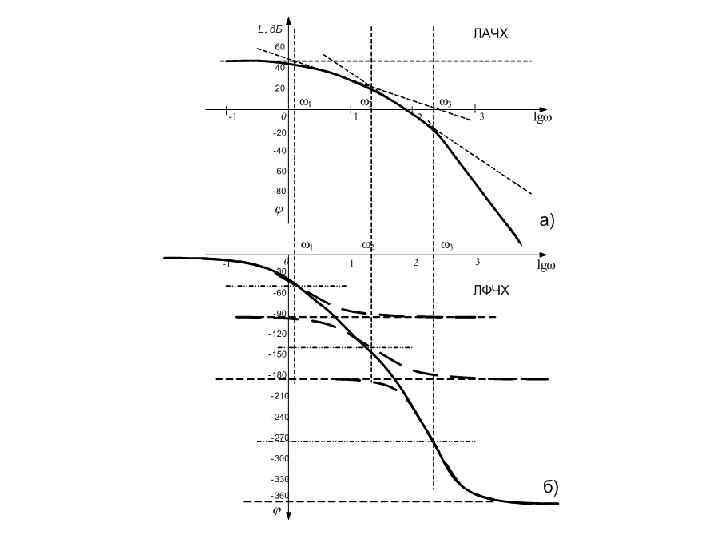
Приклад побудови логарифмічних частотних характеристик системи

Лекція № 9 Cтійкість САК

Стійкість системи – це здатність системи повертатись до попереднього чи близького до нього стану після певної дії на систему. Рис. 1 – Приклади стійкої та нестійкої системи а) стійка система; б) нестійка система; с) система на межі стійкості (стійка при малих відхиленнях і нестійка при великих)

Система стійка тоді і тільки тоді, коли всі корені характеристичного рівняння являються або дійсними від’ємними, або комплексними з від’ємною дійсною частиною. Це правило – ознаку стійкості – можна сформулювати наступним чином: для стійкості системи необхідно і достатньо, щоб усі корені характеристичного рівняння мали від’ємні дійсні частини. Корисно представити геометричну інтерпретацію цієї ознаки. Позначимо корені характеристичного рівняння на комплексній площині. Наприклад, для трьох коренів характеристичного рівняння 3 -го порядку. Якщо корені мають від’ємну дійсну частину, то вони знаходяться в лівій півплощині. Тоді формулювання ознаки стійкості буде таким: для стійкості системи необхідно і достатньо, щоб всі корені характеристичного рівняння знаходилися у лівій півплощині (3 -4 квадратні) комплексної змінної.

Правило Стодоли Необхідною умовою стійкості системи повинна бути додатність коефіцієнтів характерного рівняння розімкненої системи.

Критерій Рауса Система стійка, якщо перший стовпчик таблиці Рауса, складеної з коефіцієнтів характеристичного рівняння системи >0.

Алгебраїчний критерій стійкості Рауса-Гурвіца Система стійка, якщо діагональний визначник Гурвіца та його мінори >0. Визначник Гурвіца складається із коефіцієнтів характеристичного рівняння системи і має такий вигляд: Коефіцієнти відсутні в характеристичному рівнянні системи, що досліджується заміняються нулями. Наприклад, в рівнянні 4 -го порядку є тільки коефіцієнти . Тому при його дослідженні коефіцієнти і т. д. приймають рівними 0. Мінори визначника Гурвіца:

Формули для визначення стійкості САК за критерієм Гурвіца Визначення запасу стійкості за критерієм Гурвіца Система більш стійка, чим більші визначники Гурвіца від 0. Якщо , то система знаходиться на межі стійкості. Із рівняння граничної стійкості можна визначити критичне значення будь-якого параметра САК. Приклад:

Частотний критерій стійкості Михайлова Запишемо характеристичне рівняння, через характеристичний поліном (многочлен): де дійсна частина буде містити парні степені : а уявна – непарні степені :

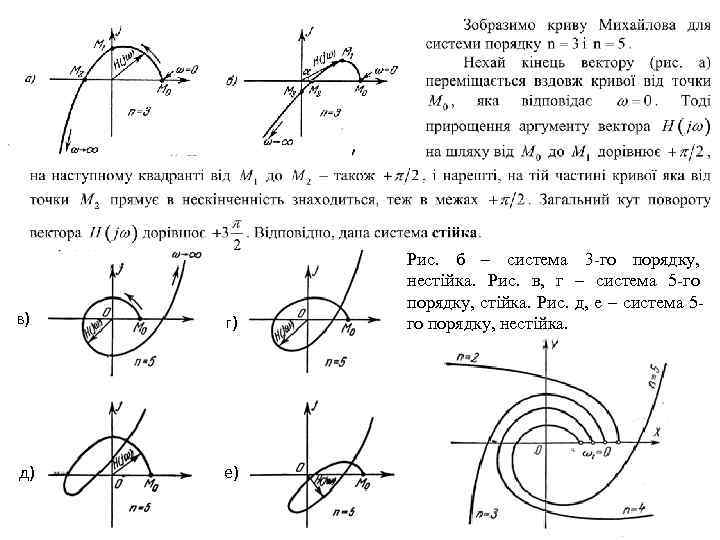в) г) д) е) Рис. б – система 3 -го порядку, нестійка. Рис. в, г – система 5 -го порядку, стійка. Рис. д, е – система 5 го порядку, нестійка.