Теория автоматического управления Лекция 9 Частотные критерии устойчивости

Теория автоматического управления Лекция 9. Частотные критерии устойчивости

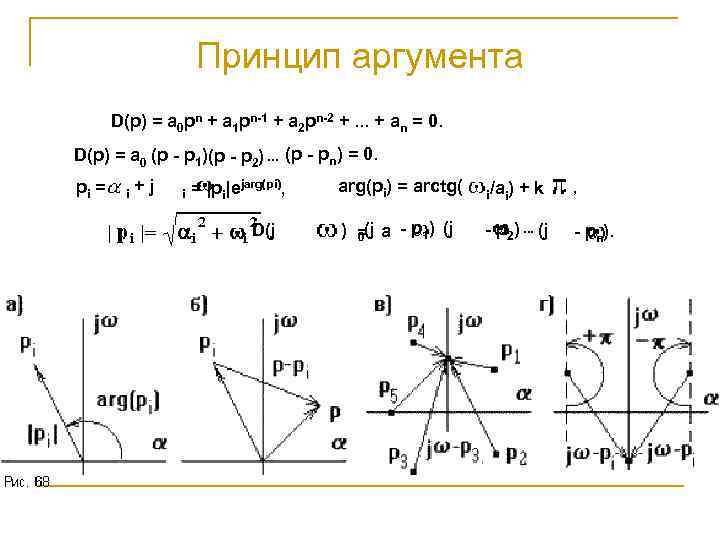Принцип аргумента D(p) = a 0 pn + a 1 pn-1 + a 2 pn-2 +. . . + an = 0. D(p) = a 0 (p - p 1)(p - p 2). . . (p - pn) = 0. pi = i +j i = |pi|ejarg(pi), D(j arg(pi) = arctg( i/ai) ) =(j a - p 1) (j 0 - p 2). . . (j +k , - pn).

Критерий устойчивости Михайлова n n n Чтобы все корни ХУ: a 0 s n + a 1 s n-1 +. . . + an-1 s + an = 0 , имели отрицательные вещественные части, необходимо чтобы после подстановки частоты в соответствующий характеристический полином D(s) полное приращение его фазы при изменении ω от 0 до ∞ составляло nπ/2, где n - степень полинома D(s). При этом характеристический полином опишет в комплексной плоскости кривую - "годограф Михайлова". Представим D(s) в виде разложения на линейные множители и выполним подстановку s=jω: D(jω) = a 0 (jω - s 1) (jω - s 2). . . (jω - sn) , где: s 1, s 2, . . . , sn - корни ХУ. Скобки идентичны, поэтому рассмотрим одну из них. Возможны четыре основных варианта:

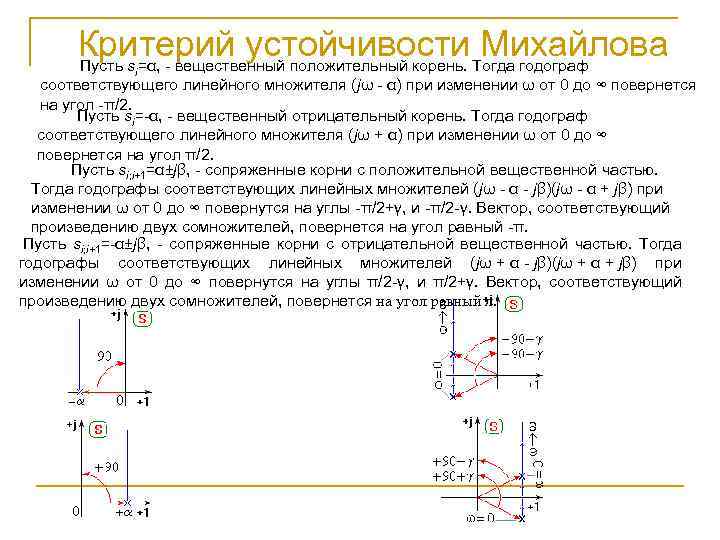Критерий устойчивости Михайлова Пусть si=α, - вещественный положительный корень. Тогда годограф соответствующего линейного множителя (jω - α) при изменении ω от 0 до ∞ повернется на угол -π/2. Пусть si=-α, - вещественный отрицательный корень. Тогда годограф соответствующего линейного множителя (jω + α) при изменении ω от 0 до ∞ повернется на угол π/2. Пусть si; i+1=α±jβ, - сопряженные корни с положительной вещественной частью. Тогда годографы соответствующих линейных множителей (jω - α - jβ)(jω - α + jβ) при изменении ω от 0 до ∞ повернутся на углы -π/2+γ, и -π/2 -γ. Вектор, соответствующий произведению двух сомножителей, повернется на угол равный -π. Пусть si; i+1=-α±jβ, - сопряженные корни с отрицательной вещественной частью. Тогда годографы соответствующих линейных множителей (jω + α - jβ)(jω + α + jβ) при изменении ω от 0 до ∞ повернутся на углы π/2 -γ, и π/2+γ. Вектор, соответствующий произведению двух сомножителей, повернется на угол равный π.

Критерий устойчивости Михайлова Резюме: Если ХУ имеет l корней с положительной вещественной частью, то угол поворота годографа D(jω) при изменении ω от 0 до ∞ составит: ψ = - l π/2 + (n - l) π/2 = n π/2 - l π , где: n - порядок ХУ. Свойства годографа Михайлова Годограф всегда спиралевиден. При ω=0, будет ψ=0. Следовательно, годограф начинается с точки на оси "+1". Поскольку при ω→∞ K(jω)→ 0 (нет безынерционных систем), годограф уходит в бесконечность. При четном n, годограф стремится к ∞ параллельно оси "+1"; при нечетном n, годограф стремится к ∞ параллельно оси "+j".

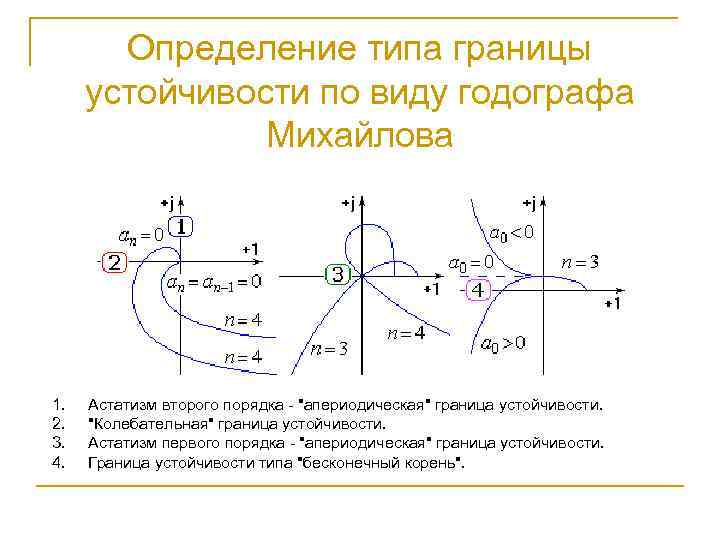Определение типа границы устойчивости по виду годографа Михайлова 1. 2. 3. 4. Астатизм второго порядка - "апериодическая" граница устойчивости. "Колебательная" граница устойчивости. Астатизм первого порядка - "апериодическая" граница устойчивости. Граница устойчивости типа "бесконечный корень".

Критерий устойчивости Найквиста Чтобы система в замкнутом состоянии была устойчивой необходимо и достаточно, чтобы при изменении ω от -∞ до +∞ годограф разомкнутой системы W(jω) (АФХ), поворачиваясь вокруг начала координат по часовой стрелке, охватил точку (-1, j 0) столько раз, сколько корней в правой полуплоскости содержит знаменатель W(jω). Примечания: Если корней в правой полуплоскости нет, то годограф W(jω) не должен охватить точку (-1, j 0). Неустойчивая система в разомкнутом состоянии может быть устойчивой в замкнутом состоянии. И наоборот. Годограф W(jω) всегда начинается на оси "+1". Но при порядке астатизма равном r, по причине устремления W(jω) к ∞ (при ω→ 0), видимая часть годографа появляется только в квадранте r, отсчитанном по часовой стрелке.

Критерий устойчивости Найквиста Рассмотрим ПФ для статической САР сдвинутую на величину (-1, j 0): W 1(s) = 1+ W(s) = Q(s)/Q(s) + R(s)/Q(s) = D(s)/Q(s) , в ней D(s) - характеристический полином, Q(s) пусть не имеет корней в правой полуплоскости (пусть W(s) устойчива). Рассмотрим угол поворота годографа W 1(s). Он равен φ = φ1(D(jω)) φ2(Q(jω)). Поскольку степень полинома R(s) всегда меньше степени полинома Q(s), то степени полиномов числителя и знаменателя ПФ W 1(s) равны. Следовательно, при изменении ω от -∞ до +∞ имеем: φ1(D(jω))=nπ (по критерию Михайлова), φ2(Q(jω))=nπ (по предположению об отсутствии корней в правой полуплоскости у полинома Q(s)). Т. е. φ=nπ-nπ=0. Другими словами для устойчивости САР в замкнутом состоянии W 1(jω) не должна охватывать начала координат, а функция W(jω) - точку (-1, j 0). Если знаменатель будет содержать l корней в положительной полуплоскости, то угол поворота годографа W(jω) должен составить величину: φ = φ1(D(jω)) - φ2(Q(jω)) = n π - [(n - l) π - l π] = l 2π ,

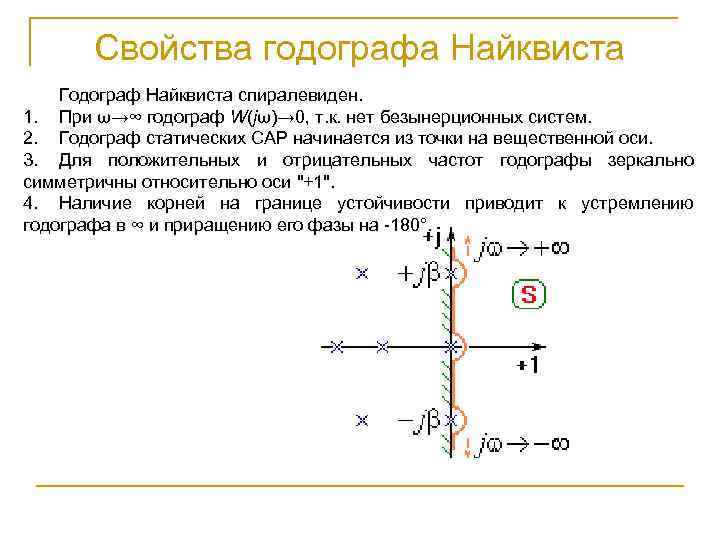Свойства годографа Найквиста Годограф Найквиста спиралевиден. 1. При ω→∞ годограф W(jω)→ 0, т. к. нет безынерционных систем. 2. Годограф статических САР начинается из точки на вещественной оси. 3. Для положительных и отрицательных частот годографы зеркально симметричны относительно оси "+1". 4. Наличие корней на границе устойчивости приводит к устремлению годографа в ∞ и приращению его фазы на -180°.

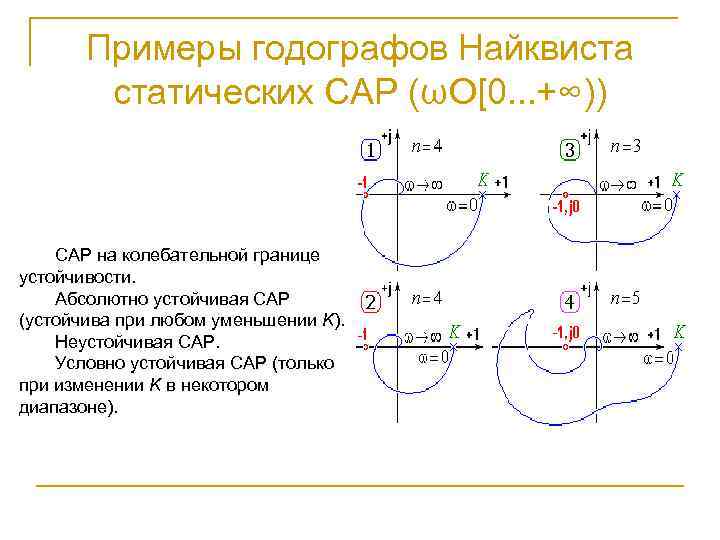Примеры годографов Найквиста статических САР (ωО[0. . . +∞)) САР на колебательной границе устойчивости. Абсолютно устойчивая САР (устойчива при любом уменьшении K). Неустойчивая САР. Условно устойчивая САР (только при изменении K в некотором диапазоне).

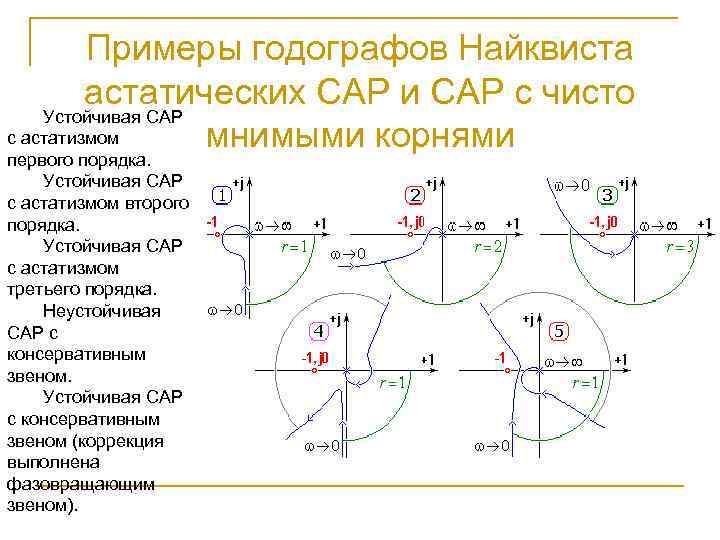Примеры годографов Найквиста астатических САР и САР с чисто Устойчивая САР с астатизмом мнимыми корнями первого порядка. Устойчивая САР с астатизмом второго порядка. Устойчивая САР с астатизмом третьего порядка. Неустойчивая САР с консервативным звеном. Устойчивая САР с консервативным звеном (коррекция выполнена фазовращающим звеном).