теоретическая механика Лектор к т н

теоретическая механика Лектор – к. т. н. , доцент Коньшин Дмитрий Владимирович

СТАТИКА 1. Основные понятия Материальная точка – объект бесконечно малых размеров, обладающий только одним свойством – массой. Механическая система – любая совокупность материальных точек. Абсолютно твердое тело – механическая система, расстояние между точками которой не изменяется при любых взаимодействиях. Силой называют одну из векторных мер механического действия одного материального объекта на другой. Сила характеризуется модулем, точкой приложения, линией действия, следовательно, является величиной векторной. Система сил – любая совокупность сил. Системы сил, оказывающие одинаковое действие на твердое тело, называются эквивалентными. Система сил, эквивалентная нулю, не изменяет состояния тела (механической системы) и называется уравновешенной.

1. 1. Аксиомы статики 1. Аксиома о равновесии системы двух сил. 2. Аксиома о добавлении (отбрасывании) системы сил, эквивалентной нулю. 3. Аксиома параллелограмма сил.

Справедливо и обратное положение: силу можно разложить по двум направлениям по правилу параллелограмма: R = F 1 + F 2; Проецирование силы на координатные оси Если силы заданы проекциями на координатные оси, то их сумму можно найти аналитическим способом:

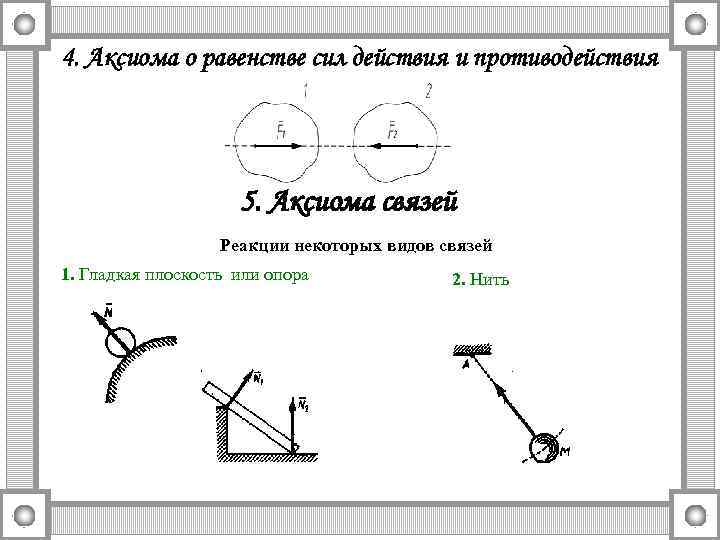4. Аксиома о равенстве сил действия и противодействия 5. Аксиома связей Реакции некоторых видов связей 1. Гладкая плоскость или опора 2. Нить

а) шарнирно подвижная опора (Рис. 4) запрещает только непод вертикальное перемещение Рис. 4 б) цилиндрический плоский шарнир (шарнирно – вижная опора) (Рис. 5) Рис. 5 в) сферический (шаровой) шарнир г) жесткая (плоская) заделка (Рис. 6) запрещает линейные переме (Рис. 7) запрещает два линей щения вдоль трёх координатных осей, ных и угловое перемещения Рис. 6 Рис. 7 где: R – реакция опоры; X, Y, Z – проекции этой силы на координатные оси.

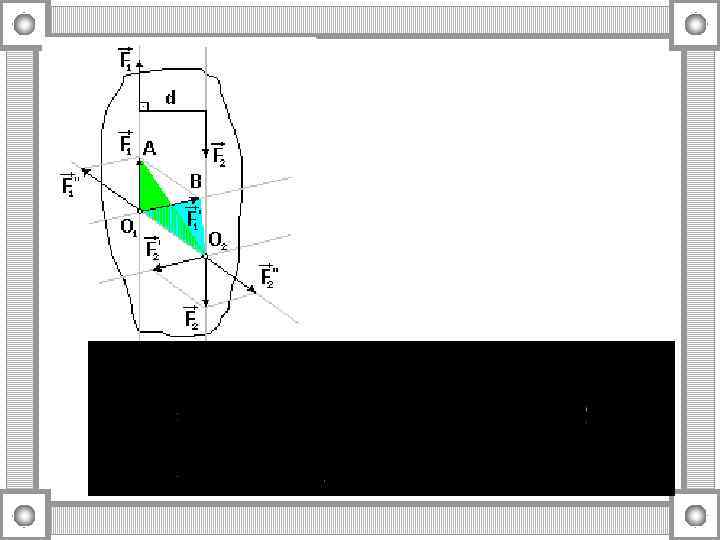
1. 2. Теоремы статики 1. Теорема о переносе силы вдоль линии действия. F' = F F" = -F. 2. Теорема о трех силах.

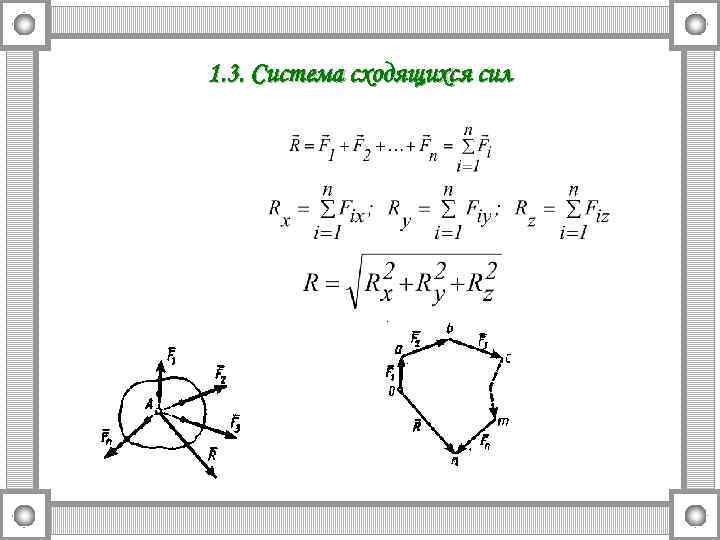1. 3. Система сходящихся сил

Условия равновесия системы сходящихся сил в аналитическом виде: – для произвольной системы сил. – для плоской системы сходящихся сил.

1. 4. Момент силы относительно точки и оси 1. Алгебраический момент силы относительно точки. . F – сила; h – плечо силы Мо - момент

2. Векторный момент силы относительно точки

3. Момент силы относительно оси Примечание: а) Mz=0, если сила параллельна оси Oz. б) Mz=0, если линия действия пересекает ось Oz.

4. Связь момента силы относительно оси с векторным моментом силы относительно точки на оси

5. Пара сил и алгебраический момент пары сил.

.

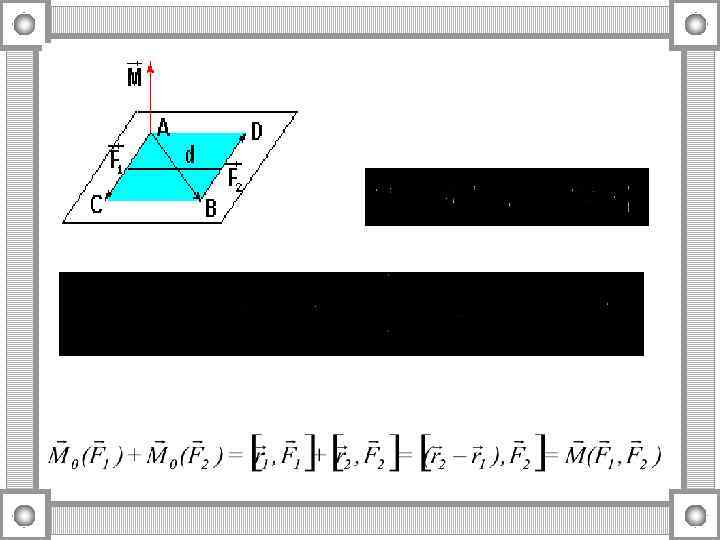1. 5. Приведение системы сил к простейшей системе

Главным вектором системы сил называют вектор, равный векторной сумме этих сил (вектор R). Значение главного вектора сил не зависит от выбора точки приведения.

Главным моментом системы сил относительно точки О тела называют сумму векторных моментов всех сил системы относительно этой точки (вектор момента результирующей пары М 0). По проекциям сил можно найти модуль главного вектора и главного момента, а также косинусы их углов с осями координат.

1. 6. Условия равновесия систем сил Пространственная система сил Система параллельных сил Rx=Ry=Rz=0; Mx=My=Mz=0, Пусть Fi параллельно оси Oz, тогда Mz тождественно равно нулю и Таким образом, имеем три уравнения равновесия

Плоская система сил После отбрасывания тождеств: имеем три уравнения равновесия: Для плоской системы параллельных сил имеем лишь два уравнения равновесия:

Теорема о моменте равнодействующей силы (теорема Вариньона). Добавим к этой системе сил , тогда

Так как , то имеем теорему Вариньона: Это справедливо и в любых проекциях, например то есть для плоской системы сил имеем теорему Вариньона в алгебраических моментах:

Различные формы условий равновесия плоской системы сил: 1. Ранее приведенная система 2. Эквивалентная ей система уравнений равновесия для любых трех точек, не лежащих на одной прямой. 3. Также эквивалентная первой система

1. 7. Центр масс Центром масс механической системы называется точка G(xm, ym, zm) с координатими: где суммирование производится по всем точкам системы, mi – масса i той точки системы, M масса всей системы. Для сплошных тел суммы переходят в интегралы:

Методы определения центров масс. а) Метод разбиения на части. где ri – радиус-вектор центра i-той части, Si – площадь i-той части.

б) Метод отрицательных масс

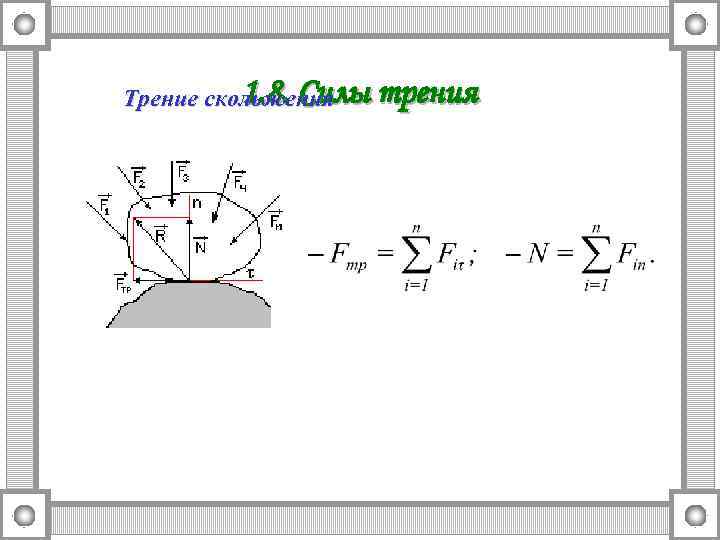1. 8. Силы трения Трение скольжения

Законы Кулона для сухого трения скольжения Примерные значения коэффициента трения кирпич-бетон………………. . 0, 76, сталь-сталь…………………. . 0, 15, дуб-дуб (поперек волокон)… 0, 54, дуб-дуб (вдоль волокон)……. 0, 62.

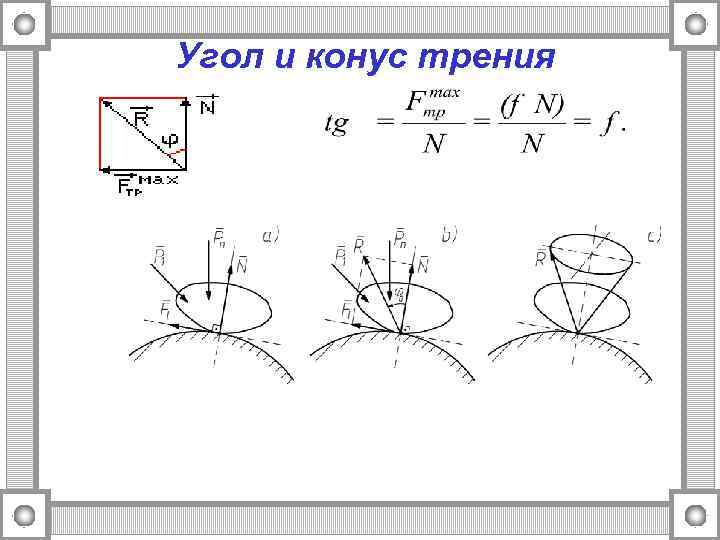Угол и конус трения

Трение качения Законы Кулона для трения качения: Mmax = δN

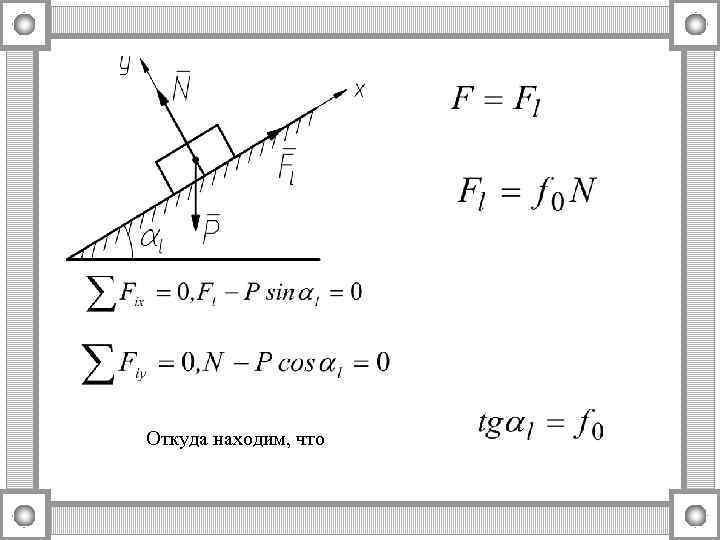Откуда находим, что

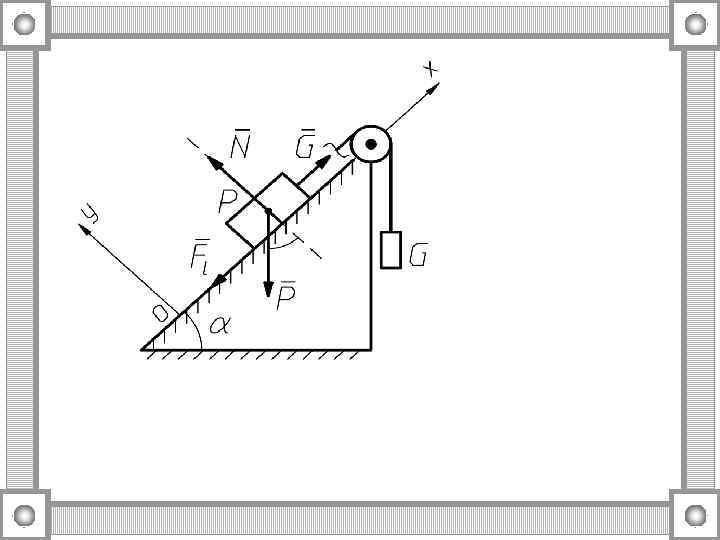
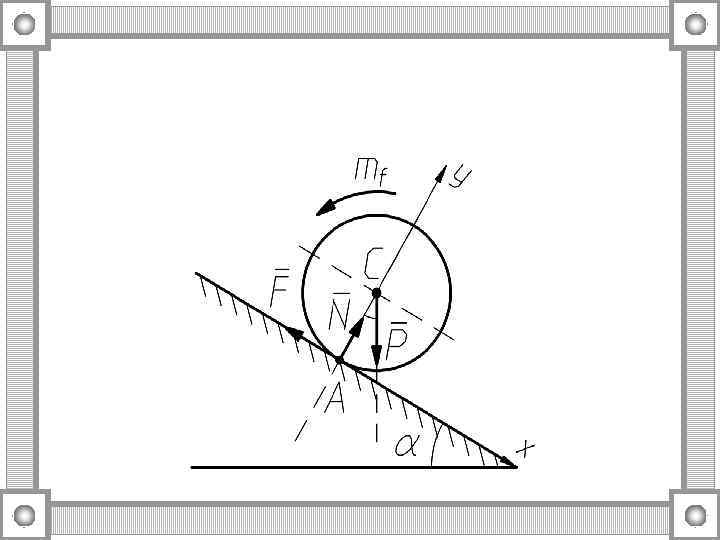
2. КИНЕМАТИКА точки 2. 1. Кинематика точки. Скорость и ускорение в декартовых координатах

Обозначим через S длину дуги траектории, отсчитываемой с соответствующим знаком от первоначального положения точки на траектории: Тогда, очевидно,

2. 2. Скорость и ускорение точки в естественной системе координат Определим орт , он направлен по касательной к траектории. где k − кривизна траектории, R − радиус кривизны траектории

Определим скорость и ускорение точки в естественной системе координат: то есть Таким образом, скорость точки всегда направлена по касательной к траектории. то есть

2. 3. Скорость и ускорение точки в полярных координатах Для скорости получаем : Для производной по времени от единичного вектора имеем:

После этого для скорости точки в полярных координатах получаем: Таким образом, радиальная и трансверсальная составляющие вектора скорости имеют вид:

Для ускорения легко получить:

2. 4. Скорость и ускорение точки в цилиндрических координатах Разложение векторов скорости и ускорения на составляющие, параллельные осям цилиндрической системы координат Or , Op , Oz выразится в следующей форме:

где – единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоско сти с осями. Ox и Oy. Представим радиус вектор точки М как сумму двух векторов, т. е.

Скорость точки получим дифференцированием радиус вектора времени: по В итоге для скорости получается следующее разложение на составляющие осям цилиндрической системы координат:

Ускорение точки получим дифференцированием по времени вектора скорости:

Получим выражение для ускорения точки в состав ляющих, параллельных осям цилиндрической системы координат:

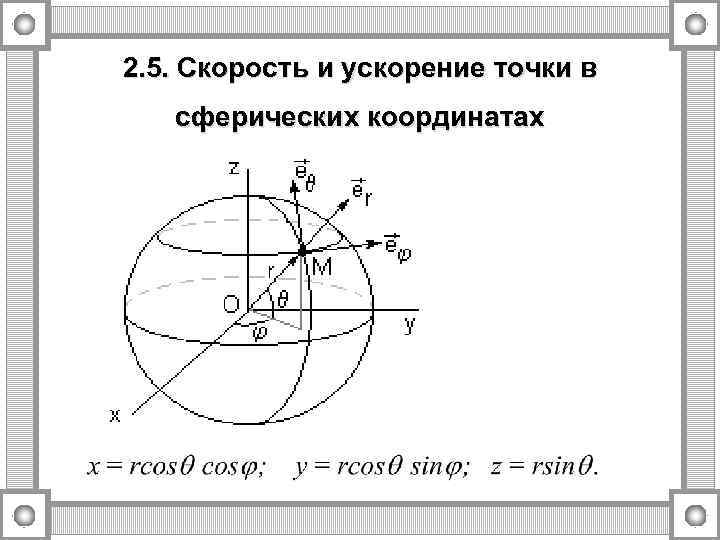2. 5. Скорость и ускорение точки в сферических координатах

Для скорости и ускорения аналогично цилиндрическим координатам (либо через коэффициенты Ламэ можно получить следующие выражения:

2. 6. Движение: абсолютное, относительное, переносное Теорема Эйлера. Угловая скорость

2. 7. Сложное движение точки

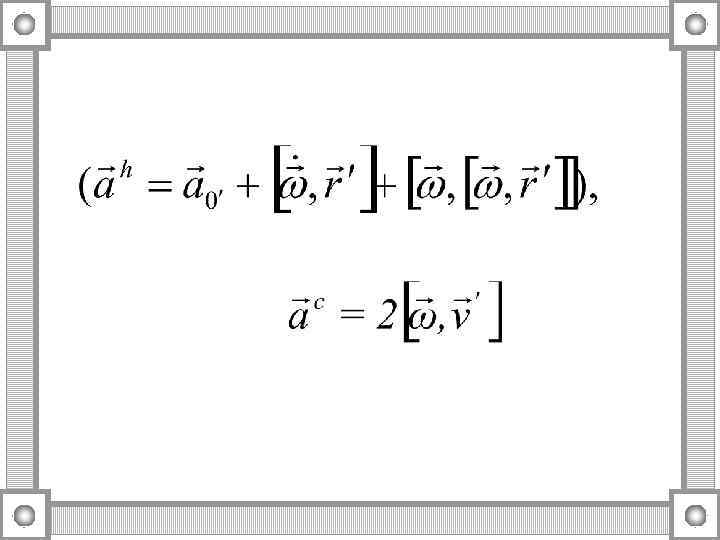
2. 8. Степени свободы. Теорема о проекциях

2. 9. Поступательное движение твердого тела

неподвижной оси

2. 11. Скорости и ускорения точек тела при вращении

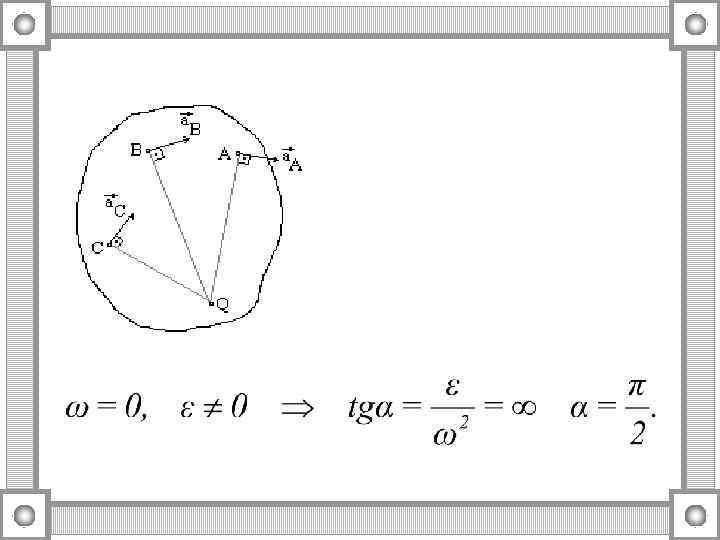
т. к. для окружности r = h. Обозначив a угол между полным ускорением точки и ее радиусом вращения, имеем:

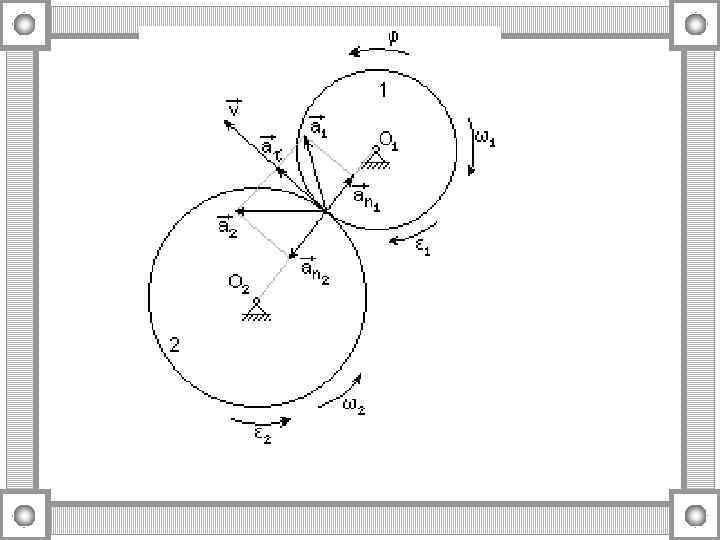
Векторы угловой скорости и ускорения − векторная формула Эйлера

2. 12. Плоское движение твердого тела М будем иметь координаты:

2. 13. Скорость точек тела при плоском движении Мгновенный центр скоростей

Скорость точки Р равна нулю, если

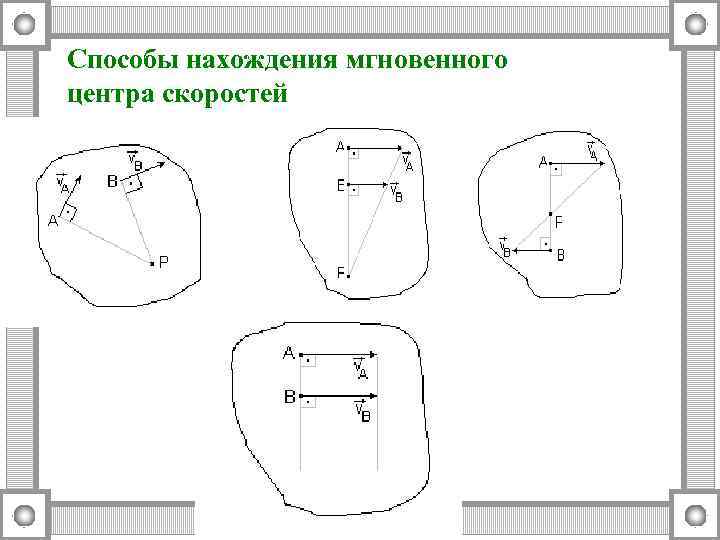Способы нахождения мгновенного центра скоростей

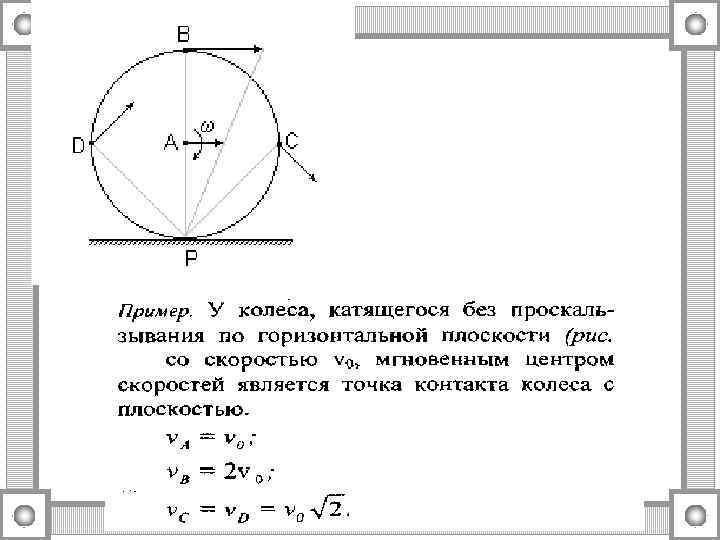
Вычисление угловой скорости при плоском движении

2. 14. Ускорения точек при плоском движении тела Мгновенный центр ускорений Эту формулу можно представить в виде отсюда

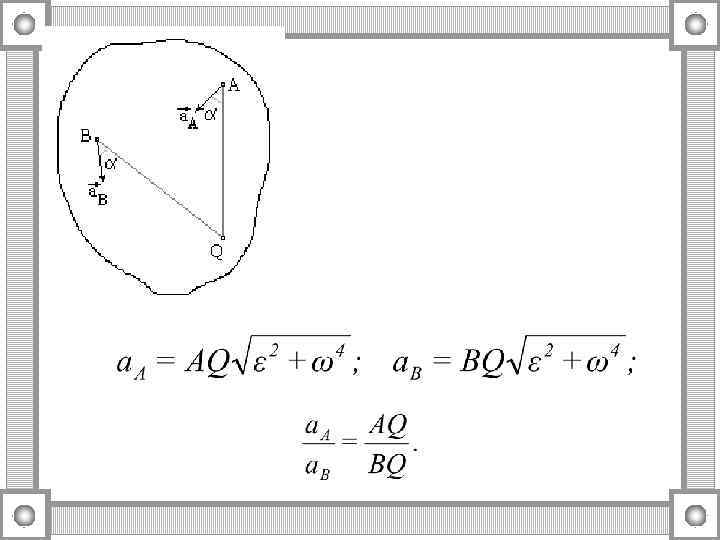
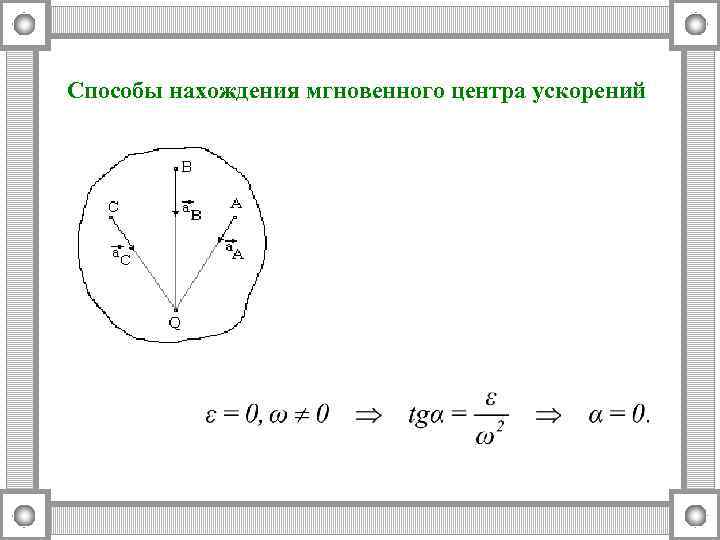Способы нахождения мгновенного центра ускорений