Теорема Пифагора n Пифагор Самосский ок 580

Теорема Пифагора

n Пифагор Самосский (ок. 580 - ок. 500 до н. э. ) древнегреческий математик и философ-идеалист. Родился на острове Самос. Получил хорошее образование.

Скульптуры Пифагора

Великие открытия Пифагора-математика нашли и по всему миру. В наибольшей степени это касается теоремы Пифагора. Которую он доказал 8 тысяч лет назад. Но немногие знают о том, что Пифагор был великим философом. Однако его учение не сохранилось до наших дней. Вместе с его учениками, которые были разбросаны по всему миру после смерти наставника, умер и великий труд мастера. Люди знают об учении Пифагора по пересказам древних философов.

n Хаммурапи - царь Вавилона Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Поэтому нам ничего не остается, как рассмотреть некоторые классические доказательства теоремы Пифагора, известные из древних трактатов. Немногим больше сведений есть о теореме Пифагора, применяемой у вавилонян. В найденном тексте, который относят к временам Хаммурапи, а это 2000 год до н. э. , есть приблизительное определение гипотенузы прямоугольного треугольника.

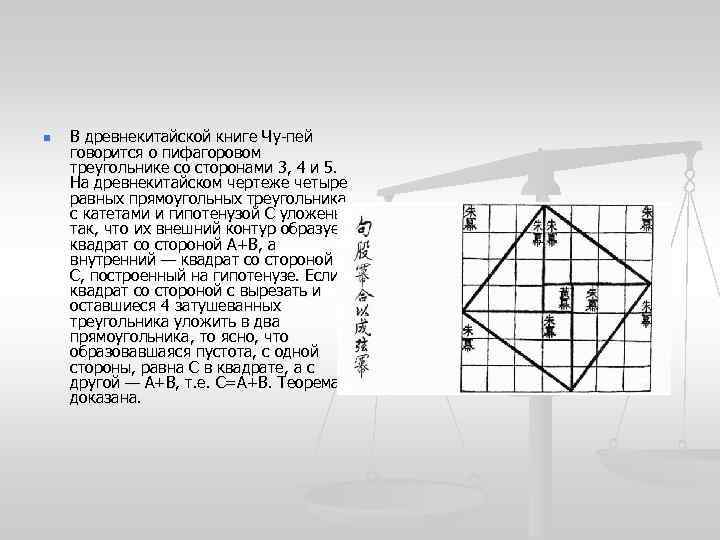n В древнекитайской книге Чу-пей говорится о пифагоровом треугольнике со сторонами 3, 4 и 5. На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами и гипотенузой С уложены так, что их внешний контур образует квадрат со стороной А+В, а внутренний — квадрат со стороной С, построенный на гипотенузе. Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника, то ясно, что образовавшаяся пустота, с одной стороны, равна С в квадрате, а с другой — А+В, т. е. С=А+В. Теорема доказана.

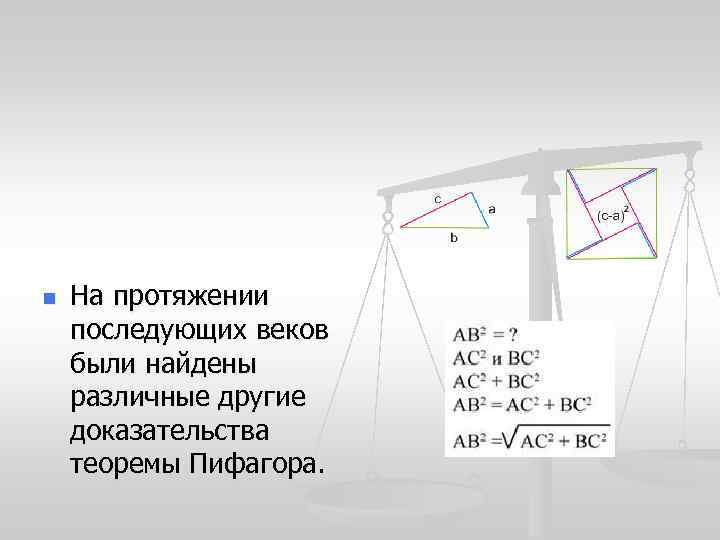n На протяжении последующих веков были найдены различные другие доказательства теоремы Пифагора.

n n n Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Доказательство. Пусть Δ ABC прямоугольный и ∠ ABC – прямой. Проведем высоту BD из вершины B прямого угла. По определению косинуса угла n Сложим полученые равенства и получим: n n Теорема доказана.

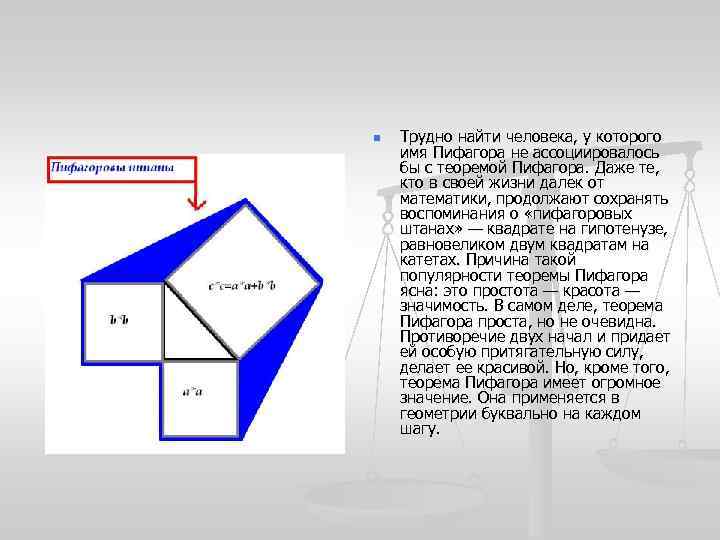n Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Даже те, кто в своей жизни далек от математики, продолжают сохранять воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора ясна: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Противоречие двух начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение. Она применяется в геометрии буквально на каждом шагу.

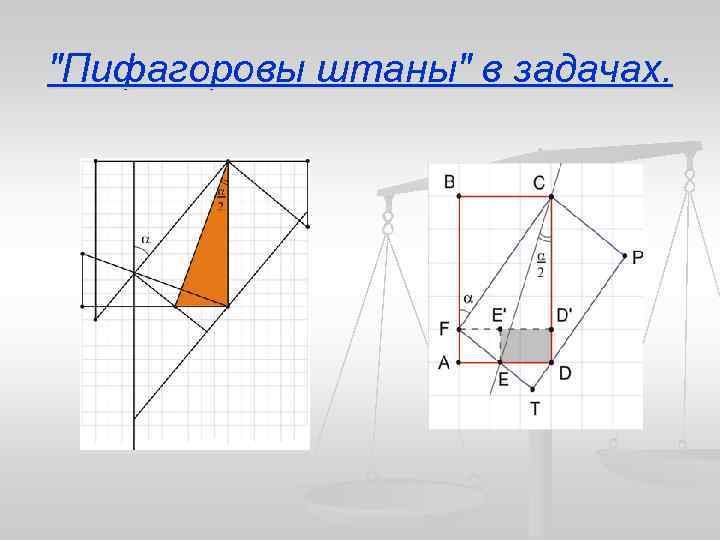"Пифагоровы штаны" в задачах.

n n n Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков. У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

Доказательство Евклида: n Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал". n n n n На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник ICEL - квадрату АСКС. Тогда сумма квадратов на катетах будет равна квадрату на гипотенузе. В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними: FB = AB, BC = BD РFBC = d + РABC = РABD n n n Но SABD = 1/2 S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=12 S ABFH (BF-общее основание, АВ-общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH. Аналогично, используя равенство треугольников ВСК и АСЕ, доказывается, что SJCEL=SACKG. Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED, что и требовалось доказать.

Евклид - древнегреческий ученый

n n n Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало 12 в. ), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол". В Geometria Culmonensis (около 1400 г. ) в переводе теорема читается так : "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу". В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

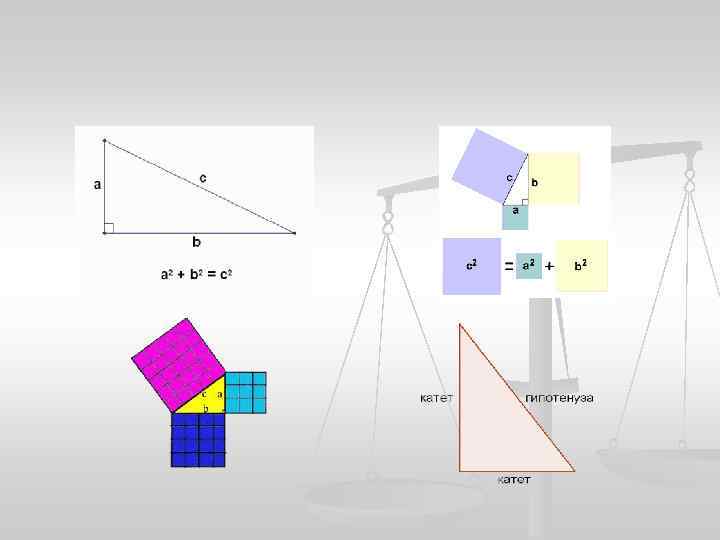
ПРОСТЕЙШЕЕ ДОКАЗАТЕЛЬСТВО: n n «Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах» . Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для такого треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по 2. Теорема доказана.

АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА: n n n Пусть Т— прямоугольный треугольник с катетами а, b и гипотенузой с. Докажем, что с2=а 2+Ь 2. Построим квадрат Q со стороной а+Ь. На сторонах квадрата Q возьмем точки А, В, С, D так, чтобы отрезки АВ, ВС, CD, DA отсекали от квадрата Q прямоуголь¬ные тре-угольники Т 1, Т 2, Т 3, Т 4 с катетами а и b. Четырех¬угольник ABCD обозначим буквой Р. Пока-жем, что Р — квадрат со стороной с. Все треугольники Т 1, Т 2, Т 3, Т 4 равны треугольнику Т (по двум катетам). Поэтому их гипотенузы равны гипотенузе треугольника Т, т. е. отрезку с. Докажем, что все углы этого четырехугольника прямые. Пусть и — величины острых углов треугольника Т. Тогда, как вам известно, + = 90°. Угол у при вершине А четырехугольника Р вместе с углами, равными и , состав¬ляет развернутый угол. Поэтому + =180°. И так как + = 90°, то =90°. Точно так же доказывается, что и остальные углы четырехугольника Р прямые. Следователь¬но, четырехугольник Р — квадрат со стороной с. Квадрат Q со стороной а+Ь слагается из квадрата Р со стороной с и четырех треугольников, равных треуголь¬нику Т. Поэтому для их площадей выполняется равенство S(Q)=S(P)+4 S(T). Так как S(Q)=(a+b) 2 ; S(P)=c 2 и S(T)=1/2(ab), то, подставляя эти выражения в S(Q)=S(P)+4 S(T), получаем равенство ( a+b) 2=c 2+4*(1/2)ab. Поскольку(a+b)2=a 2+b 2+2 ab, то равенство (a+b)2=c 2+4*(1/2)ab мож¬но записать так: a 2+b 2+2 ab=c 2+2 ab. Из равенства a 2+b 2+2 ab=c 2+2 ab следует, что с2=а 2+Ь 2. Ч. Т. Д.

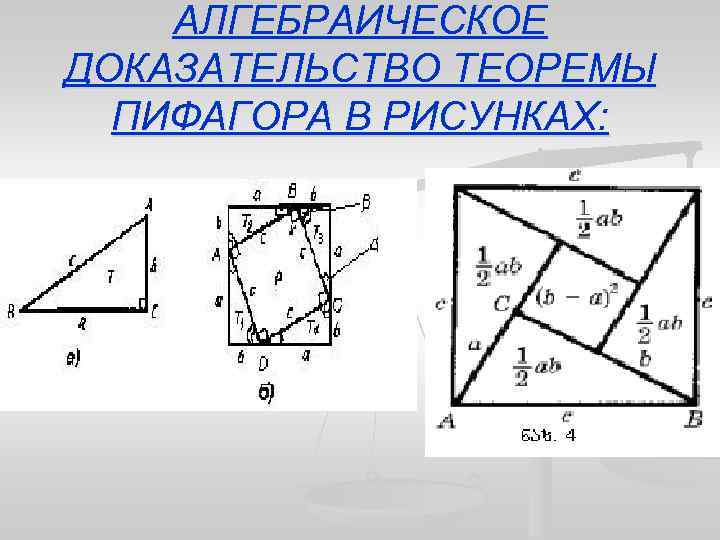АЛГЕБРАИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ПИФАГОРА В РИСУНКАХ:

n Пифагор сделал полезное открытие. С помощью его теоремы решаются многие задачи по геометрии, в школе и не только.