Тема: «Собственные векторы и собственные значения матрицы»

Тема: «Собственные векторы и собственные значения матрицы» Основные понятия: 1. Определения 2. Нахождение собственных значений матрицы 3. Нахождение собственных векторов матрицы завершить

1. Определения Ненулевой вектор х называется собственным вектором матрицы А, если найдется такое число , что Число называется собственным ( характеристическим ) значением ( числом ) матрицы А, соответствующим вектору х. далее. Ax x

Характеристическим уравнением матрицы А называется уравнение: Пример 1. назад 11 12 1 21 22 2 1 2. . . 0. . . . n n nna a a A E a a a

Пример 1. Составить характеристические уравнения для матриц Решение : 1 0 1 2 4 ,

Решение (Пример 1) : Составим характеристическое уравнение для матрицы А: далее 2 4 1 0 0 5 0 1 2 4 1 0 0 0 5 0 1 2 4 0.

Решение (Пример 1) : Составим характеристическое уравнение для матрицы В: назад 1 0 1 1 0 0 0 1 2 0 0 1 0 0 8 0 1 0 0 1 1 2 0 0.

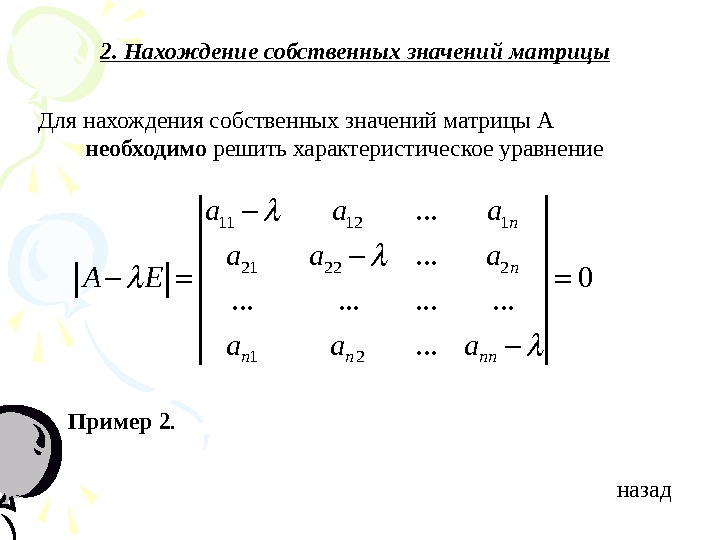
2. Нахождение собственных значений матрицы Для нахождения собственных значений матрицы А необходимо решить характеристическое уравнение Пример 2. назад 11 12 1 21 22 2 1 2. . . 0. . . . n n nna a a A E a a a

Пример 2. Найти собственные значения матриц Решение : 1 0 1 2 4 ,

Решение (Пример 2) : Решим характеристическое уравнение матрицы А: далее 2 4 0 0 5 2, 2 5 0 5.

Решение (Пример 2) : Решим характеристическое уравнение матрицы В: назад 2 1 0 1 1 2 0 0 8 0 1 1 2 1 8 2 0 2, 2 9 0 3, 3.

3. Нахождение собственных векторов матрицы Для нахождения собственных векторов матрицы А необходимо решить систему линейных однородных уравнений Пример 3. назад 0 0 A E x

Пример 3. Найти собственные векторы следующих матриц Решение : 1 0 1 2 4 ,

Решение (Пример 3) для матрицы А : 1) Решив характеристическое уравнение для матрицы А, получили 2) Для собственного значения составим систему линейный однородных уравнений: далее 1 22, 5. 12 1 1 2 2 1 1 0 2 4 0 0 5 0 4 0, , 0 4 0 0 3 0 0 ; 0 , . A E x x x R x x X c c R

Решение (Пример 3) для матрицы А : 3) Для собственного значения составим систему линейный однородных уравнений: далее 25 2 1 2 2 2 1 2 1 2 5 2 2 4 0 0 0 5 0 3 4 0, 3 4 0 0 4 ; 3 , . x A E x x x x X c c c R

Решение (Пример 3) для матрицы В : 1) Решив характеристическое уравнение для матрицы В, получили 2) Для собственного значения составим систему линейный однородных уравнений: далее 1 2 32, 3, 3. 12 11 1 2 3 1 1 2 1 3 3 2 1 1 1 0 1 0 0 8 0 3 0, 0, 0, , 8 3 0 0 0; ; 0 , . x A E x x x x R x x x X c c R

Решение (Пример 3) для матрицы В : 3) Для собственного значения составим систему линейный однородных уравнений: далее 23 2 1 2 2 3 1 2 1 1 2 2 1 3 1 1 3 3 1 3 2 2 2 0 1 1 0 8 0 4 2 0, , , 0, , 2 8 4 0 2 ; ; 2 , . x A E x x x R x x x X c c R

Решение (Пример 3) для матрицы В : 4) Для собственного значения составим систему линейный однородных уравнений: назад 33 3 1 3 2 3 1 1 3 2 1 1 2 2 1 3 1 1 3 3 3 3 3 4 0 1 5 0 8 0 2 , 4 0, 1 5 0, , 5 5 4 8 2 0 4 5 ; ; 20 , . x A E x x R x x x x X c c R

Спасибо за внимание! Не забывайте готовиться к лекциям и семинарам! (Тема следующей лекции «Квадратичные формы» ) Удачи!