Тема Методы построения алгоритмов Лекция 25 11 13

Тема Методы построения алгоритмов Лекция 25. 11. 13 г. 1

Методы построения алгоритмов Для нахождения решения любой задачи с помощью компьютера необходимо пройти следующие этапы: 1. Формулировка задачи 2. Построение математической модели 3. Выбор готового алгоритма или построение нового алгоритма 4. Проверка корректности алгоритма 5. Анализ сложности алгоритма 6. Программная реализация алгоритма (написание и отладка программы) 7. Проверка корректности программы 8. Оценка сложности программы 9. Документирование программы Рассмотрим эти этапы на примере известной оптимизационной задачи, которую обычно называют задачей коммивояжера. Коммивояжер (от франц. commis voyageur) - путешествующий в коммерческих целях разъездной агент торговой фирмы, предлагающий покупателям товары по имеющимся у него образцам, каталогам. Лекция 25. 11. 13 г. 2

Задача коммивояжера. Коммивояжеру для совершения торговых сделок требуется объехать n городов и вернуться в свой родной город, при этом в каждом городе он может побывать только один раз. Среди множества возможных маршрутов требуется найти тот, который позволит минимизировать затраты на поездку. Этап 1. Формулировка задачи В общем виде условие задачи уже сформулировано. Однако в каждой задаче может потребоваться сформулировать необходимые и/или дополнительные условия и ограничения, а также возможные допущения. Например: §Формализация понятия «стоимость» : предположим, что для каждой нары городов a и b задана функция стоимости C: (a, b)→c, c≥ 0, т. е. для каждой пары городов задано неотрицательное число c (время, затраченное на проезд, стоимость билета, расстояние между городами и т. п. ); §Функция стоимости учитывает направление движения, поэтому C(a, b) в общем случае не равно C(b, a); §Запрет «вырожденного» переезда из города в этот же город: C(a, a)=∞; §Спрос на товары во всех городах одинаков, и единственное, чем определяются предпочтения при выборе маршрута - это функция стоимости C. Лекция 25. 11. 13 г. 3

Задача коммивояжера Этап 2. Построение математической модели Смысл этого этапа: привлечь для решения задачи математический аппарат, который присущ данной модели, а также дать возможность использовать уже известные для данной математической модели приемы и способы нахождения требуемых результатов. Сеть из n городов можно описать как полносвязный взвешенный ориентированный граф (орграф), т. е. множество из n вершин, каждая из которых связана с любой другой ребром и при этом каждому ребру приписано направление движения и стоимость переезда. Такой граф можно представить (n×n) - матрицей смежности C, в которой каждый элемент cij содержит стоимость переезда из города i в город j. Граф является стандартным представлением для множества объектов и связей между ними. Существует большое количество практически полезных задач и алгоритмов на графах. Представление маршрутов и городов в виде графа для задачи коммивояжера даст возможность рассматривать решение задачи как поиск пути в графе, удовлетворяющего некоторым условиям. Лекция 25. 11. 13 г. 4

Задача коммивояжера Лекция 25. 11. 13 г. 5

Задача коммивояжера Пронумеруем города целыми числами от 1 до n. Тогда маршрут коммивояжера можно задать последовательностью чисел, соответствующую порядку посещаемых городов, при этом каждое число от 1 до n должно присутствовать в этой последовательности ровно один раз. Согласно принятой терминологии такой маршрут является гамильтоновым контуром на графе (по имени ирландского математика Уильяма Роуэна Гамильтона, который в 1859 г. первым начал изучение подобных задач). Лекция 25. 11. 13 г. 6

Задача коммивояжера Маршрут коммивояжера, удовлетворяющий условию задачи, задается перестановкой целых чисел Каждому маршруту π можем поставить в соответствие функцию стоимости где cij - элементы матрицы смежности С. Тогда искомое решение можно записать как Пример: Лекция 25. 11. 13 г. 7

Оптимальный маршрут для 37 городов России Лекция 25. 11. 13 г. http: //lmatrix. ru 8

Задача коммивояжера Этап 3. Выбор или построение алгоритма На этом этапе нужно: §выбрать один из известных алгоритмов решения данной задачи (наиболее подходящий по какому-то критерию), или §предложить модификацию известных алгоритмов, или §построить новый алгоритм. С точки зрения построения алгоритма данный этап кажется основным, и часто под этим этапом и понимают собственно решение задачи. Однако это не совсем верно, так как успешно выполненные начальные этапы могут значительно упростить нахождение алгоритма, а последующие этапы являются необходимыми для оценки его качества. В нашем случае наиболее очевидным и прямым методом нахождения оптимального маршрута может быть полный перебор всех возможных маршрутов. Так как любой маршрут представляет замкнутый цикл, то первый город, с которого начинаем маршрут, можно зафиксировать, и тогда всего существует (n - 1)! различных маршрутов. Для каждого из них можно вычислить его стоимость и выбрать маршрут, обеспечивающий минимальную стоимость. Лекция 25. 11. 13 г. 9

Задача коммивояжера Для 4 -х городов из выше представленной матрицы стоимостей существует 3! = 6 маршрутов (предполагается, что любой маршрут начинается из города А и заканчивается там же). Так как в рассматриваемом примере стоимость проезда между двумя любыми городами одинакова вне зависимости от направления движения, все объезды разбиваются на пары маршрутов с одинаковой стоимостью, различающихся лишь направлением объезда. Кратчайшие маршруты ACBDA и ADBCA дают минимальную стоимость 15. Лекция 25. 11. 13 г. 10

Задача коммивояжера Этап 4. Проверка корректности алгоритма Для любого предложенного алгоритма должна быть показана его корректность, т. е. доказано, что при любых входных значениях задачи алгоритм завершится, и полученный ответ будет соответствовать требуемому в условии задачи. Так как в качестве метода решения в предыдущем пункте предложили полный перебор всех вариантов, и число этих вариантов конечно, то это может служить гарантией того, что задача всегда будет решена, и решена корректно. Этап 5. Анализ сложности (трудоемкости) алгоритма Оценка сложности алгоритма может производиться как по числу операций, которые нужно выполнить для решения задачи (в среднем или в худшем случае), так и по объему требуемой памяти. В нашей задаче всего существует (n - 1)! маршрутов, их можно генерировать динамически или хранить в памяти, в любом из этих вариантов сложность нахождения полного перебора оценивается функцией O(n!), что эквивалентно экспоненциальному порядку сложности. Вдобавок, нужно хранить матрицу стоимостей из n×n ячеек. Таким образом, предложенный алгоритм приемлем лишь при малых значениях n (порядка двух-трех десятков), так как экспоненциальная функция растет чрезвычайно быстро. Лекция 25. 11. 13 г. 11

Задача коммивояжера Этап 6. Реализация алгоритма На практике, кроме разработки алгоритма, требуется и его программная или в некоторых случаях аппаратная реализация. Как правило, каждый алгоритм может быть реализован различными способами, более или менее эффективными в зависимости от самого алгоритма, условий реализации (язык программирования, операционная система, элементная база для аппаратной реализации, тип процессора и т. д. ), квалификации программиста. Конкретная реализация может быть «заточена» под конкретные требования или ограничения по памяти или времени выполнения. Если рассматриваем просто некую «среднюю» реализацию без специфических требований и ограничений, то в нашем примере для этого достаточно уметь представлять абстрактные типы данных, такие, как граф, и генерировать перестановки. И то, и другое имеет свои известные способы и методы реализации. Таким образом, при реализации одного алгоритма может потребоваться и знание вопросов реализации других алгоритмов. Лекция 25. 11. 13 г. 12

Задача коммивояжера Этап 7. Проверка корректности программы Задача проверки корректности разработанной программы, или тестирование, является самостоятельной большой задачей, которой в теории алгоритмов уделяется большое внимание. Задача эта не является простой, на практике практически никогда нельзя гарантировать корректную работу сложных программ и речь может идти лишь о корректной работе в определенных условиях и в заданном диапазоне входных данных. Существуют различные методики и подходы к тестированию, к выбору и построению систем тестов. Лекция 25. 11. 13 г. 13

Задача коммивояжера Этап 8. Оценка сложности программы Время выполнения программы, а также занимаемая программой память не всегда прямо зависят от сложности лежащего в основе алгоритма. Большое влияние оказывает реализация, а также аппаратная платформа, на которой выполняется программа. Процессор, предназначенный, в первую очередь, для обработки целых чисел, как правило, хуже работает с вещественными и наоборот. Число шагов, которые выполняет программа, или число элементов, требуемых для аппаратной реализации, сильно зависят от самой реализации. Если речь идет о создании конечного продукта, то вопросы сложности реализации выходят на первый план по сравнению со сложностью алгоритмов. Иногда, бывает более выгодно реализовать «жадный» переборный алгоритм, чем более тонкий метод. Выбор и оценка алгоритмов и реализаций должны производиться здесь, исходя их конкретных требований и ограничений. Лекция 25. 11. 13 г. 14

Задача коммивояжера Этап 9. Документирование программы Этот этап почти всегда игнорируется начинающими программистами и при грамотном исполнении всегда ценится любыми пользователями или разработчиками программ. Через очень недолгое время после написания программы даже сам автор часто может не помнить всех деталей реализации. Если с программой должны работать сторонние пользователи, наличие четкого и ясного руководства по работе становится обязательным. Даже очень хорошо написанная программа может оказаться почти бесполезной в использовании и чрезвычайно трудной в модификации при отсутствии хорошего ее описания. Лекция 25. 11. 13 г. 15

Задача коммивояжера Рассмотрим программную реализацию алгоритма прямого перебора для решения задачи коммивояжера для нескольких городов России. Выберем форму представления исходных данных. Будем использовать строковый массив неопределенного размера для хранения названий городов, а также треугольную матрицу для хранения расстояний: char *city[] = {"Rostov", "Voronezh", "Volgograd", "Krasnodar", "Astrakhan", "Ryazan", "Penza"}; int N = sizeof(city)/sizeof(city[0]); int R 1[] = {577, 492, 272, 888, 1014, 951}; // from Rostov int R 2[] = {578, 847, 1001, 449, 514}; // from Voronezh int R 3[] = {704, 436, 799, 606}; // from Volgograd int R 4[] = {910, 1284, 1221}; // from Krasnodar" int R 5[] = {1221, 1144}; // from Astrakhan int R 6[] = {448}; // from Ryazan int *D[] = {R 1, R 2, R 3, R 4, R 5, R 6}; Для упрощения обработки информации вместо названий городов будем использовать их номера: int M[N]; for(int i = 0; i < N; i++) M[i] = i; Лекция 25. 11. 13 г. 16

Задача коммивояжера Рассмотрим функцию, вычисляющую длину маршрута, заданного массивом M. Пусть требуется получить из треугольной матрицы расстояние между городами с номерами j 1 и j 2. С учетом специфика матрицы мы должны обеспечить, чтобы было j 1 < j 2, поэтому при необходимости делается обмен: if(j 2 < j 1) swap(&j 1, &j 2); С учетом этого замечания искомое расстояние будет: D[j 1][j 2 -j 1 -1] int dist(int *M, int n) { int d = R 1[M[n-1]-1]; // из последнего в первый int j 1 = 0, j 2; for(int i = 1; i< n; i++) { j 2 = M[i]; if(j 2 < j 1) swap(&j 1, &j 2); d += D[j 1][j 2 -j 1 -1]; j 1 = M[i]; } return d; } Лекция 25. 11. 13 г. 17

Задача коммивояжера Рассмотрим функцию, определяющую маршрут наименьшей длины: int D_min = 0 x 7 fffffff; int *M 0; M 0 = (int *)calloc(N, sizeof(int)); void evaluation(int *M, int n) { int r = dist(M, n); if(r < D_min) { D_min = r; for(int i = 0; i < n; i++) M 0[i] = M[i]; } } Лекция 25. 11. 13 г. 18

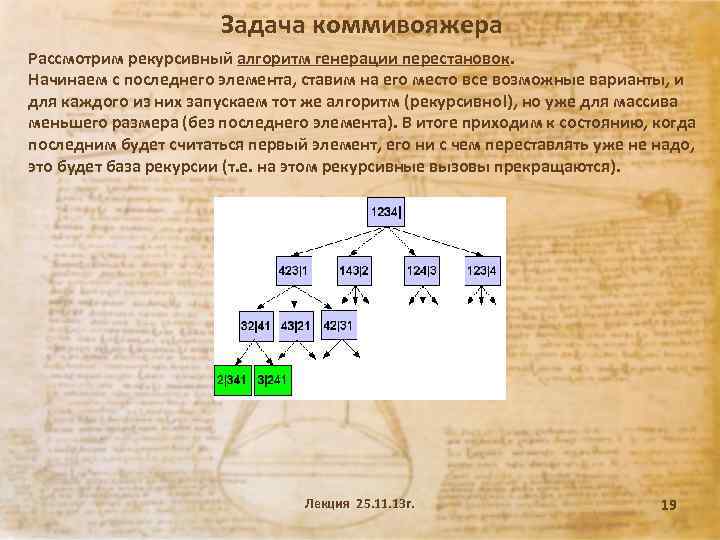Задача коммивояжера Рассмотрим рекурсивный алгоритм генерации перестановок. Начинаем с последнего элемента, ставим на его место все возможные варианты, и для каждого из них запускаем тот же алгоритм (рекурсивно!), но уже для массива меньшего размера (без последнего элемента). В итоге приходим к состоянию, когда последним будет считаться первый элемент, его ни с чем переставлять уже не надо, это будет база рекурсии (т. е. на этом рекурсивные вызовы прекращаются). Лекция 25. 11. 13 г. 19

Задача коммивояжера Обозначения: M – массив, N – размер массива (глобальная переменная), k – с какого элемента начинается перестановка, n - число переставляемых элементов. void swap(int *a, int *b) { int temp = *a; *a = *b; *b = temp; } void permutation(int *M, int k, int n) { if(n == (k + 1)) evaluation(M, N); else for(int i = k; i < n; i++) { swap(M + i, M + n - 1); permutation(M, k, n - 1); swap(M + i, M + n - 1); } } Лекция 25. 11. 13 г. 20

Полная программа. Задача коммивояжера //Ex 068_Permutation. c – генерация перестановок #include #include char *city[] = {. . . }; int N = sizeof(city)/sizeof(city[0]); int R 1[] = {577, 492, 272, 888, 1014, 951}; // from Rostov. . . int R 6[] = {448}; // from Ryazan int *D[] = {R 1, R 2, R 3, R 4, R 5, R 6}; int D_min = 0 x 7 fffffff; // плюс бесконечность int *M 0; // оптимальный маршрут void swap(int *a, int *b) {. . . } int dist(int *M, int n) {. . . } void evaluation(int *M, int n) {. . . } void permutation(int *M, int k, int n) {. . . } int main() { int M[N]; for(int i = 0; i < N; i++) M[i] = i; M 0 = (int*)calloc(N, sizeof(int)); permutation(M, 1, N); printf("Dist_min = %dn", D_min); for(int i = 0; i < N; i++) printf("%s ", city[M 0[i]]); system("PAUSE"); return 0; } Лекция 25. 11. 13 г. 21

Методы построения алгоритмов Рассмотрим три основных подхода, которые могут быть использованы при разработке алгоритмов. Суть их отражена в названиях: Øметод частных целей, Øметод подъема, Øметод отрабатывания назад. Описания этих методов являются довольно общими и не дают четких рекомендаций по поиску решения задачи, а только формулируют подходы к поиску этого решения. Для некоторой задачи может быть использован какой-то один подход или их комбинация. Лекция 30. 12 г. 22

Метод частных целей Методом частных целей называется метод поиска решения, состоящий в разбиении всей задачи на более простые подзадачи (установление частных целей), которые в совокупности дают решение исходной задачи. Конечно, мы надеемся на то, что более простые задачи легче поддаются обработке, чем первоначальная задача, а также на то, что решение первоначальной задачи может быть получено из решений этих более простых задач. Этот метод выглядит очень разумно. Но, как и большинство общих методов решения задач или разработки алгоритмов, его не всегда легко перенести на конкретную задачу. Осмысленный выбор более простых задач— скорее дело искусства или интуиции, чем науки. Более того, не существует общего набора правил для определения класса задач, которые можно решить с помощью такого подхода. Лекция 30. 12 г. 23

Метод частных целей Размышление над любой конкретной задачей начинается с постановки вопросов. Частные цели могут быть установлены, когда мы получим ответы на следующие вопросы: 1. Можем ли мы решить часть задачи? Можно ли, игнорируя некоторые условия, решить оставшуюся часть задачи? 2. Можем ли мы решить задачу для частных случаев? Можно ли разработать алгоритм, который дает решение, удовлетворяющее всем условиям задачи, но входные данные которого ограничены некоторым подмножеством всех входных данных? 3. Есть ли что-то, относящееся к задаче, что мы не достаточно хорошо поняли? Если попытаться глубже вникнуть в некоторые особенности задачи, сможем ли мы что-то узнать, что поможет нам подойти к решению? 4. Встречались ли мы с похожей задачей, решение которой известно? Можно ли видоизменить ее решение для решения нашей задачи? Возможно ли, что эта задача эквивалентна известной нерешенной задаче? Лекция 30. 12 г. 24

Простой метод сортировки массива Необходимо отсортировать в порядке возрастания числовой массив, например, такой: 13, 3, 5, 21, 7, 1, 11. Поставим частную цель: найти в массиве максимальный элемент и поменять его местами с последним элементом. В результате решения этой частной задачи сложность исходной задачи уменьшится на 1 и на следующем шаге мы будем уже иметь дело с массивом, размер которого на 1 меньше исходного массива. Таким образом, последовательно решая более простые задачи, мы получим решение поставленной задачи. 13 3 5 21 7 1 11 1 3 5 7 11 13 21 13 3 5 11 7 1 21 Лекция 30. 12 г. 1 3 5 11 7 13 21 25

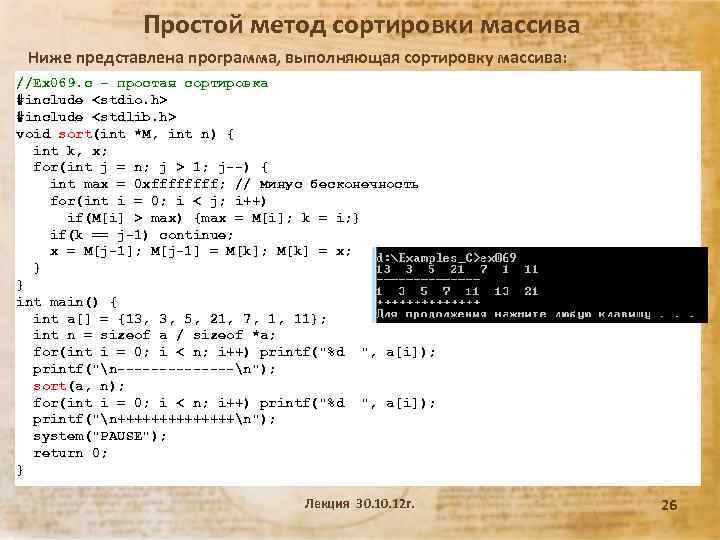Простой метод сортировки массива Ниже представлена программа, выполняющая сортировку массива: //Ex 069. c – простая сортировка #include #include void sort(int *M, int n) { int k, x; for(int j = n; j > 1; j--) { int max = 0 xffff; // минус бесконечность for(int i = 0; i < j; i++) if(M[i] > max) {max = M[i]; k = i; } if(k == j-1) continue; x = M[j-1]; M[j-1] = M[k]; M[k] = x; } } int main() { int a[] = {13, 3, 5, 21, 7, 1, 11}; int n = sizeof a / sizeof *a; for(int i = 0; i < n; i++) printf("%d ", a[i]); printf("n-------n"); sort(a, n); for(int i = 0; i < n; i++) printf("%d ", a[i]); printf("n+++++++n"); system("PAUSE"); return 0; } Лекция 30. 12 г. 26

Методы подъема и отрабатывания назад Методом подъема называется метод поиска решения, состоящий в последовательном (пошаговом) улучшении некоторого начального решения. Алгоритм подъема начинается с принятия начального предположения или вычисления начального решения задачи. Затем начинается насколько возможно быстрое движение «вверх» от начального решения по направлению к лучшим решениям. Когда алгоритм достигает такую точку, из которой больше невозможно двигаться наверх, он останавливается. К сожалению, нельзя всегда гарантировать, что окончательное решение, полученное с помощью алгоритма подъема, будет оптимальным. Этот «дефект» часто ограничивает применение метода подъема. Методом отрабатывания назад называется метод поиска решения, основанный на предположении, что задача уже решена, и состоящий в последовательном определении условий, при которых это решение может быть получено. Затем, если эти действия обратимы, движемся обратно от постановки задачи к решению. Лекция 30. 12 г. 27

Задача о пересечении пустыни Требуется пересечь на джипе пустыню шириной 1200 км, израсходовав при этом минимум горючего. Объем топливного бака джипа равен 90 литров, расход горючего составляет 15 л/100 км. В точке старта имеется неограниченный резервуар с топливом. Так как в пустыне нет складов горючего, мы должны устанавливать свои собственные хранилища и наполнять их топливом из бака машины. Где расположить эти хранилища? Сколько горючего нужно залить в каждое из них? Будем строить алгоритм решения этой задачи, используя метод частных целей и метод отрабатывания назад. Сформулируем частную цель: с какого расстояния от конца пути мы сможем пересечь пустыню, имея запас горючего в точности на k баков? Мы будем задавать этот вопрос для k =1, 2, 3, . . . , пока не найдем такое целое n, что n полных баков позволят пересечь всю 1200 -км пустыню. Для k =1 ответ равен 600 км, как и показано на рисунке. Можно заправить машину в точке В (если в этой точке есть необходимый запас горючего) и пересечь оставшиеся 600 км пустыни. Очевидно, что это наиболее отдаленная точка, стартуя из которой можно преодолеть пустыню, имея в точности 90 л горючего. A 0 км B 90 л C 600 км Лекция 30. 12 г. 1200 км 28

Задача о пересечении пустыни Мы поставили перед собой частную цель, потому что не смогли бы решить сразу исходную задачу. Мы не задаем вопрос: сколько топлива нужно машине, чтобы преодолеть заданное расстояние? Вместо этого задаем более простой, но родственный вопрос: какое расстояние можно проехать на заданном количестве топлива? Ответить на первый вопрос становится возможным, когда ответом на второй является: не меньше 1200 км. Предположим, что k=2, т. е. имеется два полных бака (180 л). Будем рассматривать этот случай, опираясь на результат для k=1. Данная ситуация иллюстрируется ниже на рисунке. Каково максимальное значение x 1 такое, что, отправляясь с 90 л горючего из точки B 1 можно перевезти достаточно горючего в точку В, чтобы завершить поездку, как в случае k=1? Пусть x 1 выражается в сотнях км. Алгоритм: а) Заправляем в B 1 полный бак (90 л), доезжаем до B, сливаем y л в бочку, оставляя столько горючего, чтобы вернуться в B 1 с пустым баком. Очевидно, что y=90 – 2 x 1*15. б) Заправляем в B 1 полный бак (90 л), доезжаем до B, доливаем y л из бочки в бак и получаем полный бак: 90 - x 1*15 + y = 90 -> 3 x 1*15 = 90 -> x 1 = 2, т. е. 200 км. x 1 A 0 км B 1 180 л C B 90 л 600 км Лекция 30. 12 г. 1200 км 29

Задача о пересечении пустыни Продолжим решение задачи для k=3, т. е. в точке B 2 имеется три полных бака (270 л). Рассуждая по аналогии, получим, что из B 2 в B 1 нужно сделать три «ходки» : на первых двух в бочку сливается по y=90 – 2 x 2*15 л горючего, а на третьей – остатки горючего в баке вместе с накопленными запасами составят 180 л: 90 – x 2*15 + 2 y = 180 -> 5 x 2*15 = 90 -> x 2 = 1. 2, т. е. 120 км. Продолжая по аналогии, получим: x 3 = 600/7, x 4 = 600/9, … , что позволяет сделать вывод: имея n баков горючего можно проехать Решением исходной задачи будет n = 8, т. к. 1+1/3+1/5+1/7+1/9+1/11+1/13+1/15 = 2. 021800422 x 1 x 2 A 0 км B 2 270 л B 1 180 л 90 л C B Лекция 30. 12 г. 600 км 1200 км 30

Задача об отмеривании жидкости Имеются неотградуированные 3 -литровый и 5 -литровый сосуды. Нужно отмерить ровно 4 литра жидкости. Разработать алгоритм для этой процедуры. Предполагается, что есть очень большой резервуар с жидкостью. Решение. Прежде всего определим доступные операции. Так как нам неизвестно ничего, кроме объема сосудов, а отмерять объем воды нужно точно, то нельзя совершать никакие действия «на глазок» . Это значит, что можно: üдолить любой сосуд до полного; üвылить содержимое любого сосуда; üесли в сосуде 1 воды меньше, чем свободного места в сосуде 2, перелить всю воду из 1 в 2; üесли в сосуде 1 воды больше, чем свободного места в сосуде 2, долить 2 из 1 до полного. Во избежание двусмысленности будем различать «переливание» воды из одной емкости в другую и «выливание» , означающее, что одна из емкостей опустошается, не меняя количества воды в другой. Заметим, что ситуация, при которой обе емкости не целиком заполнены водой, невозможна. При любой операции одна из емкостей должна либо опустошаться, либо заполняться. Лекция 30. 12 г. 31

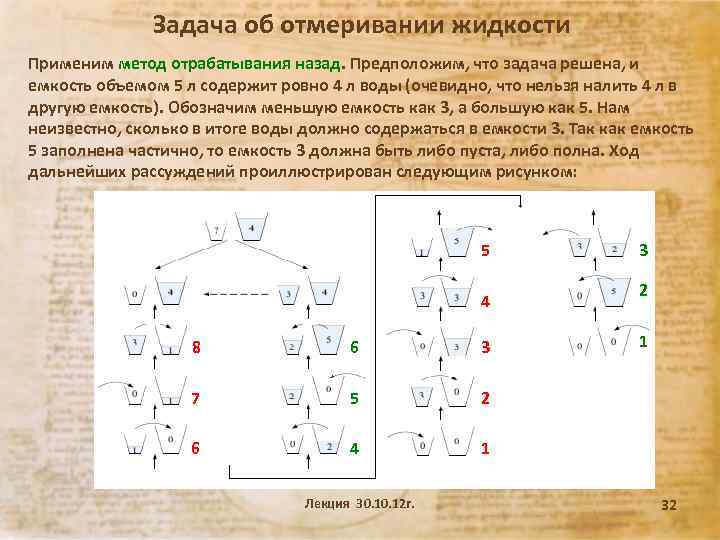Задача об отмеривании жидкости Применим метод отрабатывания назад. Предположим, что задача решена, и емкость объемом 5 л содержит ровно 4 л воды (очевидно, что нельзя налить 4 л в другую емкость). Обозначим меньшую емкость как 3, а большую как 5. Нам неизвестно, сколько в итоге воды должно содержаться в емкости 3. Так как емкость 5 заполнена частично, то емкость 3 должна быть либо пуста, либо полна. Ход дальнейших рассуждений проиллюстрирован следующим рисунком: 5 4 8 6 3 7 5 4 2 1 2 6 3 1 Лекция 30. 12 г. 32

Задача об отмеривании жидкости Итак, получили два способа переливания, тратящие различное число операций. Возможно, существуют еще решения? Подобные задачи могут быть легко решены с помощью следующего наглядного инструмента. Рассмотрим прямоугольную матрицу с сеткой, как показано на рисунке: Вертикальная сторона матрицы соответствует емкости в 3 л, горизонтальная емкости в 5 л (таким образом, числа легко могут быть обобщены). Координаты точек пересечения линий задают количество воды в двух сосудах. Если находимся в одном из узлов, то допустимой операцией является движение по любой линии до конца отрезка. Если задать начальное и искомое конечное состояния, задача сведется к поиску пути из одного узла сетки в другой. Лекция 30. 12 г. 33

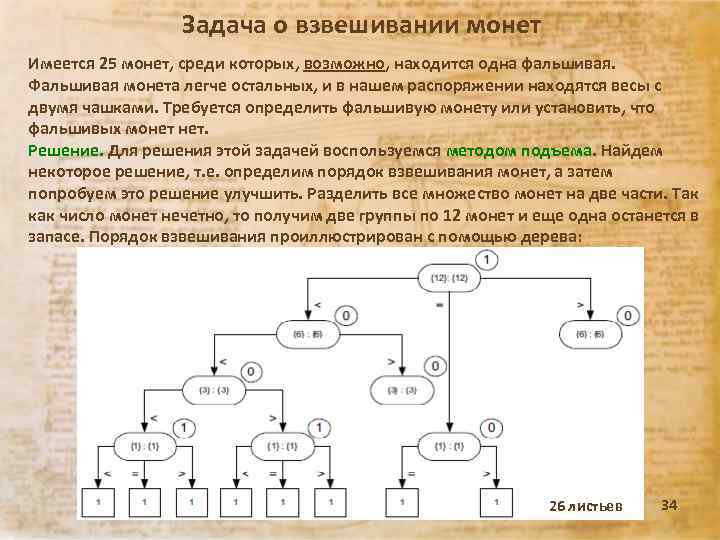Задача о взвешивании монет Имеется 25 монет, среди которых, возможно, находится одна фальшивая. Фальшивая монета легче остальных, и в нашем распоряжении находятся весы с двумя чашками. Требуется определить фальшивую монету или установить, что фальшивых монет нет. Решение. Для решения этой задачей воспользуемся методом подъема. Найдем некоторое решение, т. е. определим порядок взвешивания монет, а затем попробуем это решение улучшить. Разделить все множество монет на две части. Так как число монет нечетно, то получим две группы по 12 монет и еще одна останется в запасе. Порядок взвешивания проиллюстрирован с помощью дерева: Лекция 30. 12 г. 26 листьев 34

Задача о взвешивании монет Каждый овал задает количество взвешиваемых монет на каждой чаше весов. В кружке рядом с овалом отмечено, сколько остается монет (еще не взвешенных). Квадратами с цифрой 1 помечена ситуация, когда фальшивую монету уже можно определить однозначно. Результатом первого взвешивания могут являться три случая. . . Схема на рисунке полностью симметрична, поэтому приведена не полностью. Эта схема требует в худшем случае четырех взвешиваний. Можно ли улучшить ее так, чтобы сократить число взвешиваний? В чем главный недостаток схемы? (т. е. можно ли применить идею «подъема» ? ) Легко обнаружить, за счет чего может произойти улучшение. Дело в том, что любое взвешивание подразумевает три возможных результата: когда одна чаша весов легче, когда она тяжелее и когда весы уравновешены. Результат равенства весов используется только при первом и последних взвешиваниях и то для поиска среди двух или трех оставшихся монет. Главным нашим принципом было делить все или почти все монеты на две части, что практически исключило из дерева взвешиваний поддеревья, соответствующие равенству на весах. Лекция 30. 12 г. 35

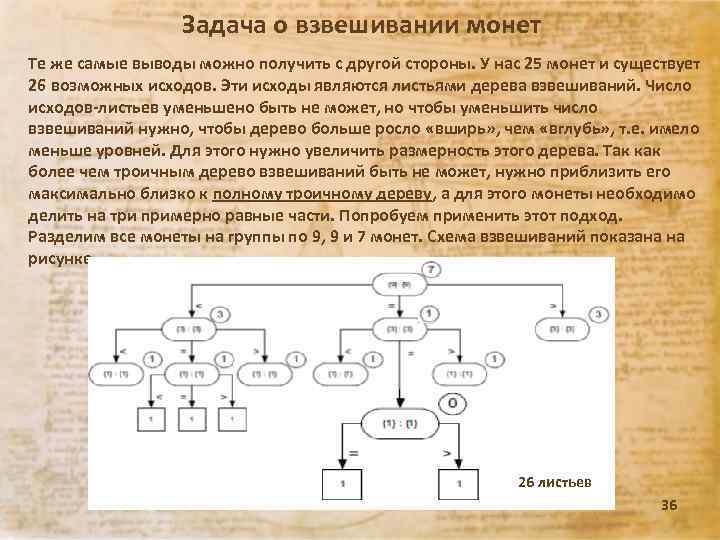Задача о взвешивании монет Те же самые выводы можно получить с другой стороны. У нас 25 монет и существует 26 возможных исходов. Эти исходы являются листьями дерева взвешиваний. Число исходов-листьев уменьшено быть не может, но чтобы уменьшить число взвешиваний нужно, чтобы дерево больше росло «вширь» , чем «вглубь» , т. е. имело меньше уровней. Для этого нужно увеличить размерность этого дерева. Так как более чем троичным дерево взвешиваний быть не может, нужно приблизить его максимально близко к полному троичному дереву, а для этого монеты необходимо делить на три примерно равные части. Попробуем применить этот подход. Разделим все монеты на группы по 9, 9 и 7 монет. Схема взвешиваний показана на рисунке. 26 листьев Лекция 30. 12 г. 36

Задача о взвешивании монет Видно, что проведенные рассуждения действительно позволили улучшить решение: теперь в худшем случае требуется только три взвешивания. Причем ясно, что еще лучше решение быть не может, так как для того, чтобы тернарное дерево имело 26 листьев, оно должно иметь как минимум 3 уровня. Задачу о взвешивании монет можно усложнить (!!!): Имеется n монет, среди которых, возможно, находится одна фальшивая. Фальшивая монета отличается от остальных по весу (т. е. может быть как легче, так и тяжелее обычной монеты), и в нашем распоряжении находятся весы с двумя чашками. Требуется определить фальшивую монету за минимальное число взвешиваний или установить, что фальшивых монет нет. Лекция 30. 12 г. 37