Скачать презентацию ТЕМА 6 Средние величины Вопросы темы 6 Скачать презентацию ТЕМА 6 Средние величины Вопросы темы 6

6 Средние величины.ppt

  • Количество слайдов: 40

ТЕМА 6 Средние величины ТЕМА 6 Средние величины

Вопросы темы: 6. 1. Сущность средних величин, их виды и значение в экономико-статистическом анализе. Вопросы темы: 6. 1. Сущность средних величин, их виды и значение в экономико-статистическом анализе. 6. 2. Порядок расчета и свойства средней арифметической. 6. 3. Порядок расчета и сфера применения средней гармонической. 6. 4. Порядок расчета и сфера применения средней геометрической и средней квадратической. 6. 5. Структурные средние: мода и медиана.

6. 1 Сущность средних величин, их виды и значение С РЕДНЯЯ ВЕЛИЧИНА - О 6. 1 Сущность средних величин, их виды и значение С РЕДНЯЯ ВЕЛИЧИНА - О Б Щ Е Н Н А Я КОЛИЧЕСТВЕННАЯ ХАРАКТЕРИСТИКА ПРИЗНАКА В СТАТИСТИЧЕСКОЙ СОВОКУПНОСТИ В КОНКРЕТНЫХ УСЛОВИЯХ МЕСТА И ВРЕМЕНИ.

Средние величины решают следующие статистические задачи: измеряют уровень развития явления; позволяют сравнивать уровень одних Средние величины решают следующие статистические задачи: измеряют уровень развития явления; позволяют сравнивать уровень одних и тех же признаков по разным совокупностям; используются для расчета показателей вариации значений признака (среднего линейного отклонения, дисперсии, среднего квадратического отклонения, относительных показателей вариации); используются при проведении корреляционнорегрессионного анализа.

СРЕДНЯЯ ВЕЛИЧИНА характеризует изучаемую совокупность по одному признаку (исключение составляет многомерная средняя) отражает уровень СРЕДНЯЯ ВЕЛИЧИНА характеризует изучаемую совокупность по одному признаку (исключение составляет многомерная средняя) отражает уровень признака, отнесенный к единице совокупности, причем не к какойто конкретной а к отвлеченной сохраняет размерность осредняемого признака

Уровень среднего значения признака формируется под влиянием двух групп факторов: Первая группа включает общие Уровень среднего значения признака формируется под влиянием двух групп факторов: Первая группа включает общие для всех единиц совокупности причины, которые формируют типичный уровень признака для всех единиц данной совокупности и связаны с сущностью изучаемого явления. Вторая группа включает индивидуальные причины, формирующие специфические особенности отдельных единиц совокупности, а, следовательно, и их отклонения от типичного уровня.

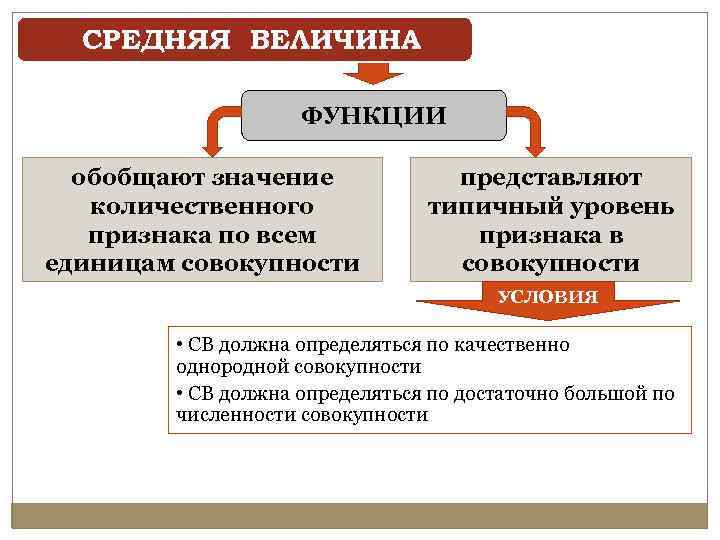СРЕДНЯЯ ВЕЛИЧИНА ФУНКЦИИ обобщают значение количественного признака по всем единицам совокупности представляют типичный уровень СРЕДНЯЯ ВЕЛИЧИНА ФУНКЦИИ обобщают значение количественного признака по всем единицам совокупности представляют типичный уровень признака в совокупности УСЛОВИЯ • СВ должна определяться по качественно однородной совокупности • СВ должна определяться по достаточно большой по численности совокупности

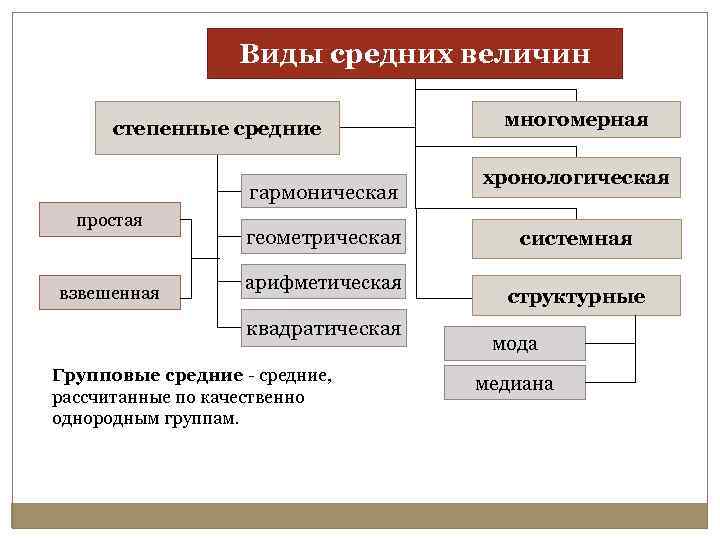Виды средних величин степенные средние гармоническая простая взвешенная геометрическая арифметическая квадратическая Групповые средние - Виды средних величин степенные средние гармоническая простая взвешенная геометрическая арифметическая квадратическая Групповые средние - средние, рассчитанные по качественно однородным группам. многомерная хронологическая системная структурные мода медиана

Многомерная средняя величина нескольких признаков для одной единицы совокупности. Она определяется из относительных величин, Многомерная средняя величина нескольких признаков для одной единицы совокупности. Она определяется из относительных величин, как правило, из отношений абсолютных значений признаков для единицы к средним значениям этих признаков. где pij - многомерная средняя для i-единицы; хij - значение признака х, для i-единицы; хj - среднее значение признака xi, k - число признаков; j - номер признака; i - номер единицы совокупности.

Системные средние характеризуют как пространственные системы, существующие одномоментно (государство, отрасль, регион), так и динамические Системные средние характеризуют как пространственные системы, существующие одномоментно (государство, отрасль, регион), так и динамические системы протяженные во времени (например, среднегодовая температура). Сравнение системных средних по разным системам (объектам), придает им признаки типичности.

Сущность степенных средних раскрывается через понятие «определяющее свойство степенных средних» . Определяющим свойством степенных Сущность степенных средних раскрывается через понятие «определяющее свойство степенных средних» . Определяющим свойством степенных средних называется их способность сохранять неизменными некоторые обобщающие количественные характеристики статистической совокупности. Обобщающая количественная характеристика совокупности, которая не изменяется при замене всех индивидуальных значений признака на его среднюю величину, называется определяющим показателем. Определяющий показатель, выраженный математически, называют определяющей функцией.

6. 2 Порядок расчета и свойства средней арифметической 6. 2 Порядок расчета и свойства средней арифметической

Порядок расчета и свойства средней арифметической Определяющим показателем средней арифметической является сумма значений признака Порядок расчета и свойства средней арифметической Определяющим показателем средней арифметической является сумма значений признака у всех единиц совокупности. В соответствии с этим, ее определяющая функция записывается следующим образом:

Средняя арифметическая На основе формулы функции составляем уравнение средней арифметической величины: Формула простой средней Средняя арифметическая На основе формулы функции составляем уравнение средней арифметической величины: Формула простой средней арифметической используется в тех случаях, когда каждое значение признака встречается один раз, либо когда при повторении значений признака они не сгруппированы.

Средняя арифметическая взвешенная: применяют в тех случаях, когда повторяющиеся по нескольку раз значения признака Средняя арифметическая взвешенная: применяют в тех случаях, когда повторяющиеся по нескольку раз значения признака сгруппированы и для каждой группы определена частота или частость значений признака

Типичные случаи расчета средней арифметической расчет средней арифметической в дискретном ряду распределения расчет средней Типичные случаи расчета средней арифметической расчет средней арифметической в дискретном ряду распределения расчет средней арифметической в интервальном ряду распределения расчет средней арифметической для совокупности в целом на основе групповых средних

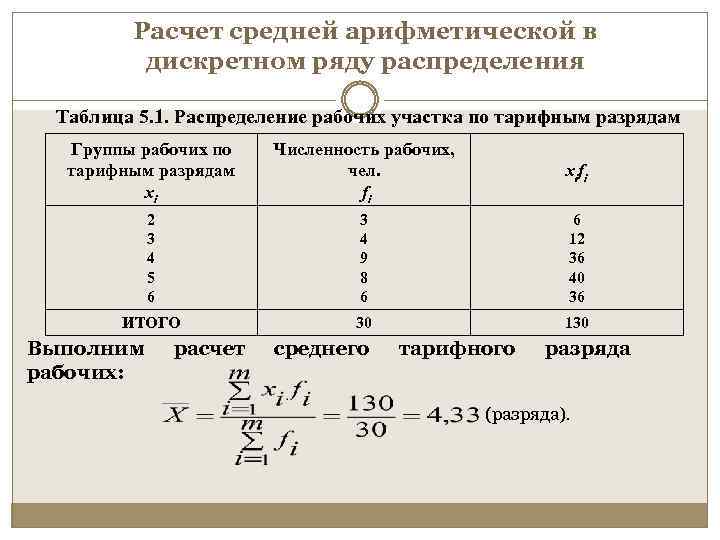Расчет средней арифметической в дискретном ряду распределения Таблица 5. 1. Распределение рабочих участка по Расчет средней арифметической в дискретном ряду распределения Таблица 5. 1. Распределение рабочих участка по тарифным разрядам Группы рабочих по тарифным разрядам хi Численность рабочих, чел. fi xifi 2 3 4 5 6 3 4 9 8 6 6 12 36 40 36 ИТОГО 30 130 Выполним рабочих: расчет среднего тарифного разряда (разряда).

Расчет средней арифметической в интервальном ряду распределения Таблица 5. 2. Распределение промышленных предприятий по Расчет средней арифметической в интервальном ряду распределения Таблица 5. 2. Распределение промышленных предприятий по среднегодовой стоимости основных производственных средств (ОПС) Группы предприятий по стоимости ОПС, млрд руб. Число предприятий, fi Удельный вес предприятий, % к итогу, ωi 3, 6 -5, 0 -6, 4 -7, 8 -9, 2 и более 2 4 6 5 3 10, 0 20, 0 30, 0 25, 0 15, 0 ИТОГО 20 100, 0

Расчет средней арифметической в интервальном ряду распределения Расчетная таблица Группы предприятий по стоимости ОПС, Расчет средней арифметической в интервальном ряду распределения Расчетная таблица Группы предприятий по стоимости ОПС, Млрд руб. 3, 6 -5, 0 -6, 4 -7, 8 -9, 2 и более ИТОГО Число предприяти й, fi Удельный вес предприятий, % к итогу, ωi 4, 3 5, 7 7, 1 8, 5 9, 9 2 4 6 5 3 10, 0 20, 0 30, 0 25, 0 15, 0 8, 6 22, 8 42, 6 42, 5 29, 5 43, 0 114, 0 213, 0 212, 5 148, 5 - 20 100, 0 146, 2 731, 0

Средняя арифметическая групповая Если известны средние значения признака по группам анализируемой совокупности, то среднее Средняя арифметическая групповая Если известны средние значения признака по группам анализируемой совокупности, то среднее значение признака по всей совокупности в целом определяется как средняя взвешенная из групповых средних: - среднее значение признака в j-ой группе; nj – численность j-ой группы.

6. 3 Порядок расчета и сфера применения средней гармонической ИСПОЛЬЗУЕТСЯ В ТЕХ СЛУЧАЯХ, КОГДА 6. 3 Порядок расчета и сфера применения средней гармонической ИСПОЛЬЗУЕТСЯ В ТЕХ СЛУЧАЯХ, КОГДА ИЗВЕСТНЫ ВАРИАНТЫ ПРИЗНАКА И ЕГО РАЗМЕР ДЛЯ СОВОКУПНОСТИ В ЦЕЛОМ, НО НЕ ИЗВЕСТНЫ ЧАСТОТЫ (ЧИСЛЕННОСТЬ СОВОКУПНОСТИ)

Порядок расчета и свойства средней гармонической Определяющим показателем средней гармонической является сумма обратных значений Порядок расчета и свойства средней гармонической Определяющим показателем средней гармонической является сумма обратных значений признака. В соответствии с этим, ее определяющая функция записывается следующим образом:

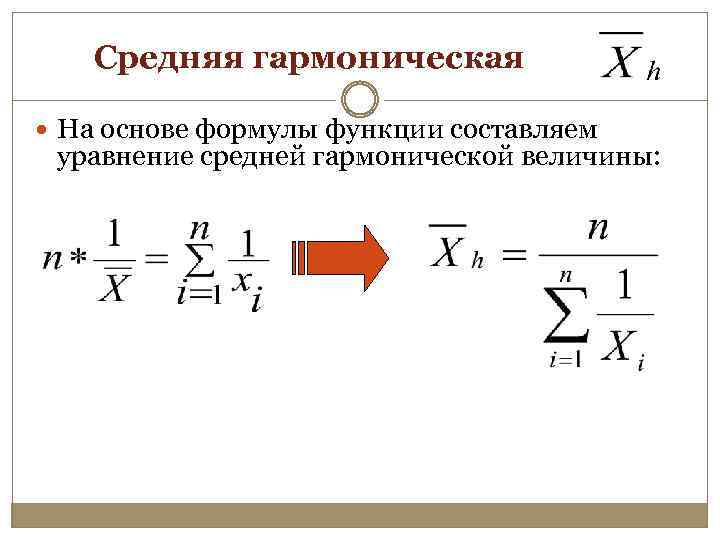Средняя гармоническая На основе формулы функции составляем уравнение средней гармонической величины: Средняя гармоническая На основе формулы функции составляем уравнение средней гармонической величины:

Средняя гармоническая Формулу средней гармонической простой используют в тех случаях, когда веса средней гармонической, Средняя гармоническая Формулу средней гармонической простой используют в тех случаях, когда веса средней гармонической, соответствующие разным значениям признака, равны между собой. Если эти веса не равны между собой, то используют формулу средней гармонической взвешенной:

Сфера применения средней гармонической (примеры): зная трудоемкость каждого вида продукции и затраты рабочего времени Сфера применения средней гармонической (примеры): зная трудоемкость каждого вида продукции и затраты рабочего времени на ее изготовление на основе средней гармонической определяют среднюю трудоемкость; известна себестоимость единицы продукции определенного вида, известнв общие затраты по цехам, но нет данных о количестве продукции; известна средняя заработная плата по цехам, известен фонд заработной платы, нет данных по численности рабочих…

Три предприятия выпускают один и тот же бытовой прибор. Себестоимость изготовления прибора составляет на Три предприятия выпускают один и тот же бытовой прибор. Себестоимость изготовления прибора составляет на каждом предприятии: 50 тыс. руб. ; 60 тыс. руб. ; 30 тыс. руб. Определить среднюю себестоимость прибора по трем предприятиям, если затраты на производство на каждом из предприятий составили по 600 000 тыс. рублей. (тыс. руб. )

Пример расчета средней гармонической взвешенной Таблица 5. 4. Средние остатки средств по срочным вкладам Пример расчета средней гармонической взвешенной Таблица 5. 4. Средние остатки средств по срочным вкладам по трем филиалам сбербанка № филиала сбербанка 1 2 3 Средний остаток по срочным вкладам, млн руб. Общая сумма остатков по срочным вкладам всех вкладчиков, млн руб. хi 1, 67 2, 80 3, 25 1897, 8 5040, 0 6987, 5 (млн руб. )

6. 4 Порядок расчета и сфера применения средней геометрической и средней квадратической 6. 4 Порядок расчета и сфера применения средней геометрической и средней квадратической

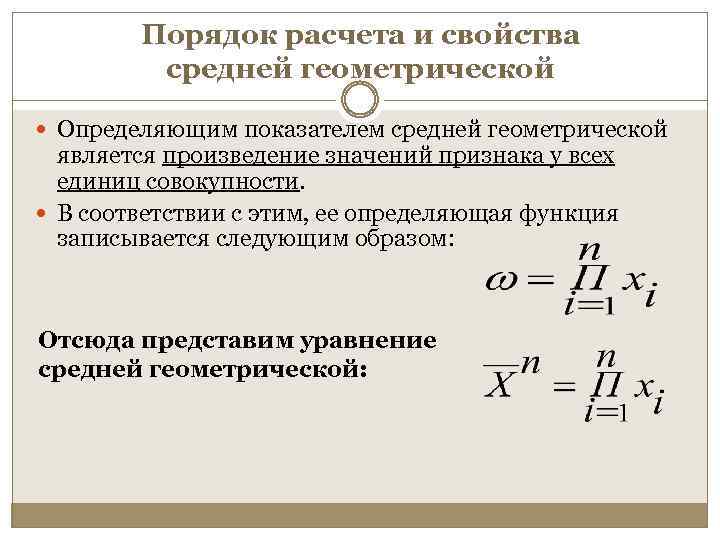Порядок расчета и свойства средней геометрической Определяющим показателем средней геометрической является произведение значений признака Порядок расчета и свойства средней геометрической Определяющим показателем средней геометрической является произведение значений признака у всех единиц совокупности. В соответствии с этим, ее определяющая функция записывается следующим образом: Отсюда представим уравнение средней геометрической:

Средняя геометрическая применяется для определения среднего коэффициента роста в рядах динамики. простая: взвешенная: Средняя геометрическая применяется для определения среднего коэффициента роста в рядах динамики. простая: взвешенная:

Средняя геометрическая используется в анализе динамики для определения средних коэффициентов (темпов) роста. Анализируется изменение Средняя геометрическая используется в анализе динамики для определения средних коэффициентов (темпов) роста. Анализируется изменение цены на продукт за 2 года. В первый год цена выросла в 3 раза, а во второй, по сравнению с первым, еще в 2 раза. Необходимо определить среднегодовой рост цены за этот период. Используем формулу средней геометрической простой: раза. Таким образом, при росте цены за 2 года в шесть раз, среднегодовой рост составил 2, 45 раза.

Порядок расчета и свойства средней квадратической Определяющим показателем средней квадратической является сумма квадратов значений Порядок расчета и свойства средней квадратической Определяющим показателем средней квадратической является сумма квадратов значений признака у всех единиц совокупности. В соответствии с этим, ее определяющая функция записывается следующим образом:

Средняя квадратическая На основе формулы функции составляем уравнение средней квадратической величины: Средняя квадратическая На основе формулы функции составляем уравнение средней квадратической величины:

Средняя квадратическая используется для расчета показателей вариации простая: взвешенная: Средняя квадратическая используется для расчета показателей вариации простая: взвешенная:

Свойство мажорантности средних: степенные средние различных видов, исчисленные по одной и той же совокупности, Свойство мажорантности средних: степенные средние различных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения, устойчиво имеющие следующее соотношение:

6. 5 Структурные средние: мода и медиана МОДА – ВЕЛИЧИНА ПРИЗНАКА, ИМЕЮЩЕГО НАИБОЛЬШУЮ ЧАСТОТУ 6. 5 Структурные средние: мода и медиана МОДА – ВЕЛИЧИНА ПРИЗНАКА, ИМЕЮЩЕГО НАИБОЛЬШУЮ ЧАСТОТУ (ЧАСТОСТЬ). МЕ Д И А Н А – ЭТО ЗНАЧЕНИЕ ПРИЗНАКА У ТОЙ ЕДИНИЦЫ СОВОКУПНОСТИ, КОТОРАЯ СТОИТ В СЕРЕДИНЕ РАНЖИРОВАННОГО РЯДА РАСПРЕДЕЛЕНИЯ.

Две моды – бимодальность. Более двух мод – мультимодальность. Модальный интервал – это Две моды – бимодальность. Более двух мод – мультимодальность. Модальный интервал – это интервал, в котором находится модальное значение признака. Медианный интервал – это интервал, для которого в графе накопленных частот мы впервые встречаем значение равное или большее половины численности совокупности.

Расчет моды в интервальном ряду с равными интервалами производится по формуле: - нижняя граница Расчет моды в интервальном ряду с равными интервалами производится по формуле: - нижняя граница модально интервала; h - величина модального интервала; - частота модального интервала.

Методика определения медианы в дискретном ряду Если число единиц совокупности (n) является нечетным, то Методика определения медианы в дискретном ряду Если число единиц совокупности (n) является нечетным, то медиана равна значению признака у единицы с порядковым номером где Если число единиц совокупности (n) является четным, то медиана равна полусумме значений признака у единиц совокупности с порядковыми номерами N 1 и N 2: где

Расчетная формула медианы в случае интервального ряда имеет вид: - нижняя граница медианного интервала; Расчетная формула медианы в случае интервального ряда имеет вид: - нижняя граница медианного интервала; - ширина медианного интервала; - накопленная частота интервала, предшествующего медианному; - частота медианного интервала; - сумма частот, или иначе – численность совокупности.