Тема 3 ОСНОВЫ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ

Тема 3. ОСНОВЫ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ

§ 1. ОПИСАНИЕ НЕЧЕТКИХ МНОЖЕСТВ, ФУНКЦИЯ ПРИНАДЛЕЖНОСТИ И ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ

Определение. Под нечетким множеством понимается множество для которого невозможно задать строгих границ.

Пусть V – полное множество, охватывающее всю предметную область. Нечеткое множество F (оно фактически является подмножеством V, но принято говорить о нем как о множестве) определяется через функцию принадлежности (u – элемент множества V). Эта функция отображает элементы и множества V на множество чисел в интервале от 0 до 1, которые указывают степень принадлежности каждого элемента нечеткому множеству F.

Если такое множество V состоит из конечного числа элементов, , то нечеткое множество F можно представить в следующем виде:

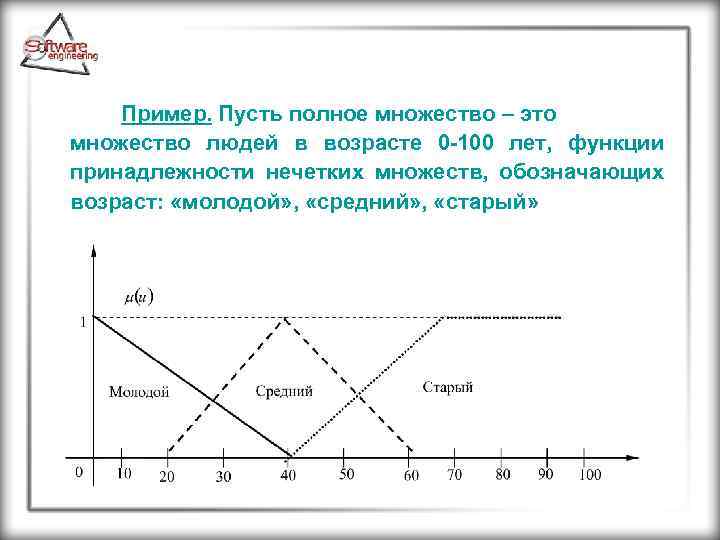Пример. Пусть полное множество – это множество людей в возрасте 0 -100 лет, функции принадлежности нечетких множеств, обозначающих возраст: «молодой» , «средний» , «старый»

В случае непрерывного используется интегральное совокупности множества V представление

Если определить множества возрастов как дискретные, отслеживая только позиции, соответствующие десятилетиям, то множества могут быть представлены в следующем виде:

Операции над нечеткими множествами 1. Дополнение множества или 2. Объединение множеств или 3. Пересечение множеств или

Пример.

§ 2. НЕЧЕТКИЕ ОТНОШЕНИЯ

Определение. Нечетким отношением R между некоторой проблемной областью (полным множеством U) и другой областью (полным множеством V) называется нечеткое подмножество прямого произведения UXV, определяемое следующим образом:

Допустим, что существует знание правит типа «если F, то G» , использующее нечеткие множества и , тогда один из способов построения нечеткого отношения из соответствующей области множества U в области множества V состоит в следующем:

Пример: Пример. Пусть U ={A, B, C, D} - множество людей, а – это множество штанг различного веса, тогда определим следующим образом нечеткие множества: F – множество сильных людей и G – множество штанг большого веса.

§ 3. СВЕРТКА ОТНОШЕНИЙ

Для построения полноценного вывода необходимо определить не только понятие отношения, но и правило перехода от одного отношения к другому, которое базируется на понятии свертки отношений. Определение. Сверткой отношений называется правило перехода от одного отношения к другому, т. е. пусть R – нечеткое отношение между областью U и областью V, а S – нечеткое отношение между V и W, тогда нечеткое отношение между U и W определяется как свертка отношений R и S

Символ « » обозначает минимаксную свертку, определяемую для выводов с помощью цепочки правил. v – взятие max для всех , - взятие min для каждой пары.

Пример. Пусть задано множество чисел - мышечной массы различного объема и на нем определено

§ 4. ПОСТРОЕНИЕ НЕЧЕТКОГО ВЫВОДА

Традиционный дедуктивный вывод (называемый правило определения) – это вывод Q из P (факта) по правилу Это записывается так

Это же обозначение используется в случаях нечетких дедуктивных выводов, если знания – это нечеткие множества а именно вывод записывается так: из по правилу

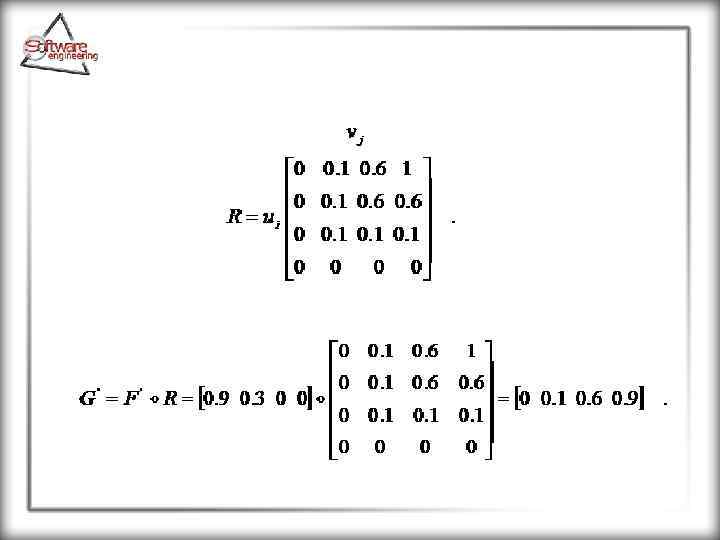
Множества F и не обязательно совпадают. Если F и близки друг к другу, то их можно сопоставить и получить вывод в области их совпадения. Конкретно нечеткие выводы представляются следующим образом. Вывод определяется из свертки множества и отношения R.

Пример. Пусть, как и в предыдущем случае