Тема 2 Анализ временных рядов n n Методы

Тема 2 Анализ временных рядов n n Методы сглаживания временных рядов Частотная фильтрация временных рядов Спектральный анализ временных рядов Стохастические модели временных рядов International Sakharov Environmental University 1

Выделение тренда и циклической компоненты Для длинных рядов выделение тренда носит обычно разведочный характер, так как часто невозможно указать подходящую параметрическую кривую для аппроксимации ряда на всей его длине. Аналогичные сложности возникают при наличии во временном ряде циклической компоненты Для выделения тренда в этом случае используют различные непараметрические методы анализа временных рядов, такие как: n n n сглаживание скользящими средними; сглаживание скользящими медианами; частотную фильтрацию и т. п. International Sakharov Environmental University 2

Выделение тренда и циклической компоненты В отличие от параметрических методов выделения тренда, эти методы пригодны лишь для осреднения значений ряда по точкам некоторой окрестности и не могут быть использованы для прогнозирования (экстраполяции) динамических рядов, поскольку не дают в явном виде расчетного уравнения детерминированной компоненты dt. Однако получение достаточно гладкой траектории дает возможность визуально оценить наличие тенденции в условиях сильной зашумленности. International Sakharov Environmental University 3

Метод скользящего среднего Метод скользящих средних основан на переходе от начальных значений ряда к их средним значениям на интервале времени, длина которого выбрана заранее. Получаемый таким образом ряд скользящих средних ведет себя гораздо более гладко, чем исходный ряд за счет усреднения отклонений исходного ряда. Применяя метод скользящего среднего можно использовать различные виды усреднения значений: n n Среднее арифметическое Взвешенное среднее арифметическое Вычисление медианы и другие Величину интервала сглаживания целесообразно выбирать равным или кратным периоду сезонности. International Sakharov Environmental University 4

Метод скользящего среднего Для интервалов сглаживания, длина которых выражается нечетными числами p=2 m+1 усреднения элементов ряда можно осуществить с помощью среднего арифметического или путем медианного сглаживания International Sakharov Environmental University 5

Метод скользящего среднего Поскольку для четных длин интервалов сглаживания p=2 m усредненное значение нельзя сопоставить какому либо определенному моменту времени t, при четной длине интервала в усреднении задействуют не 2 m, а 2 m+1 значений временного ряда. При этом значения на краях интервала сглаживания берут с весами ½. International Sakharov Environmental University 6

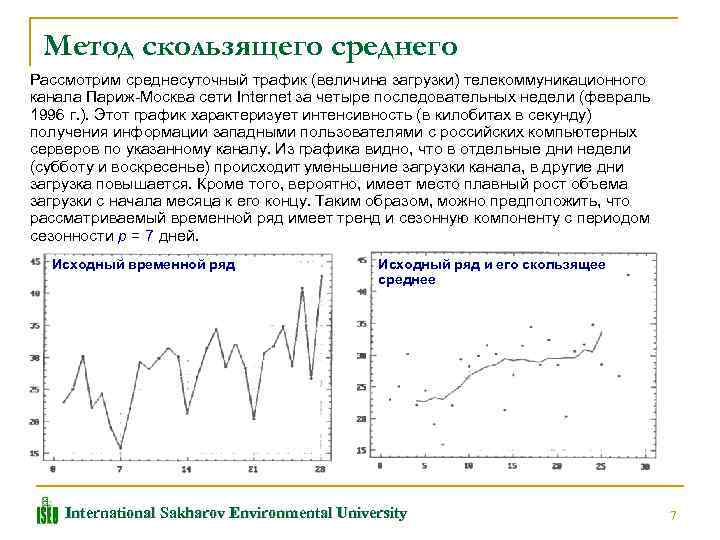Метод скользящего среднего Рассмотрим среднесуточный трафик (величина загрузки) телекоммуникационного канала Париж Москва сети Internet за четыре последовательных недели (февраль 1996 г. ). Этот график характеризует интенсивность (в килобитах в секунду) получения информации западными пользователями с российских компьютерных серверов по указанному каналу. Из графика видно, что в отдельные дни недели (субботу и воскресенье) происходит уменьшение загрузки канала, в другие дни загрузка повышается. Кроме того, вероятно, имеет место плавный рост объема загрузки с начала месяца к его концу. Таким образом, можно предположить, что рассматриваемый временной ряд имеет тренд и сезонную компоненту с периодом сезонности р = 7 дней. Исходный временной ряд Исходный ряд и его скользящее среднее International Sakharov Environmental University 7

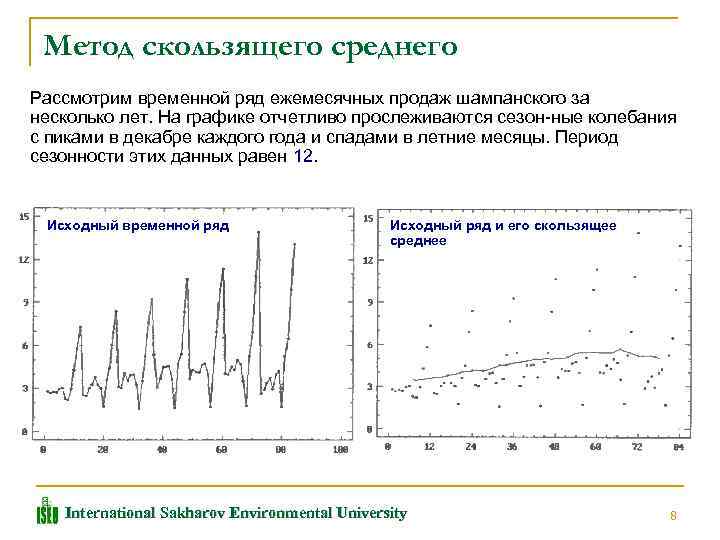Метод скользящего среднего Рассмотрим временной ряд ежемесячных продаж шампанского за несколько лет. На графике отчетливо прослеживаются сезон ные колебания с пиками в декабре каждого года и спадами в летние месяцы. Период сезонности этих данных равен 12. Исходный временной ряд Исходный ряд и его скользящее среднее International Sakharov Environmental University 8

Метод скользящего среднего. Взвешенное сглаживание состоит в определении средних, взвешенных для разных точек ряда динамики. В основе метода лежит идея локального приближения тренда полиномом не очень высокой степени. Значения оценки тренда в точке t аппроксимируются по уровням ряда из временного интервала [t - q, t + q] полиномом заданного порядка p: параметры которого оцениваются по методу наименьших квадратов с помощью уравнений типа: International Sakharov Environmental University 9

Метод скользящего среднего. Взвешенное сглаживание Решая полученные уравнения относительно ai, получим последовательность весов, зависящих только от ширины интервала (2 q + 1) и порядка полинома p, а расчет значений оценок тренда в точке t эквивалентен построению взвешенной суммы значений ряда в интервале [t q, t + q]. Для полинома порядка 1 веса ai равны между собой, что сводит этот метод к простому сглаживанию. На практике часто используется сглаживающий фильтр Хэмминга взвешенное скользящее среднее с весами 0. 25, 0. 5 и 0. 25, соответствующее формуле: International Sakharov Environmental University 10

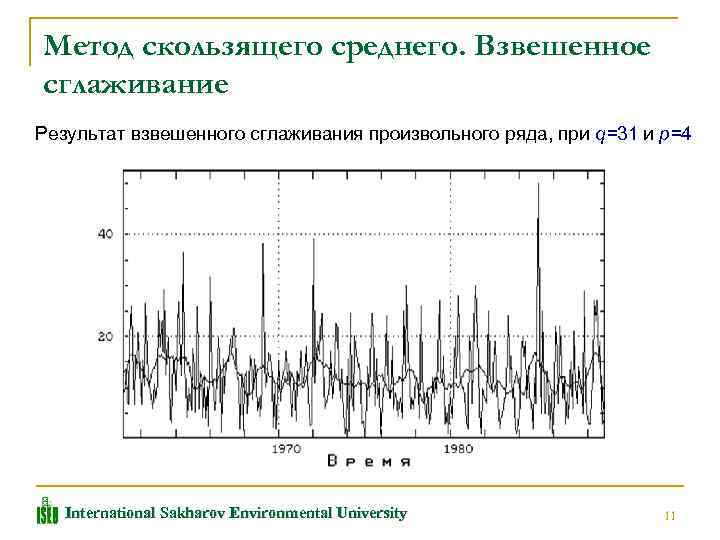Метод скользящего среднего. Взвешенное сглаживание Результат взвешенного сглаживания произвольного ряда, при q=31 и p=4 International Sakharov Environmental University 11

Метод скользящего среднего Таким образом, скользящее среднее, сглаживая исходный ряд, дает представление об общей тенденции поведения ряда – его тренде и циклической компоненте. Рассмотрим некоторые замечания по использованию скользящего среднего. n n При применении метода скользящих средних выбор величины интервала сглаживания должен делаться из содержательных предположений и привязываться к периоду сезонности для сезонных данных. Если процедура скользящего среднего используется для сглаживания несезонного ряда, то чаще всего величину интервала сглаживания выбирают равной трем, пяти или семи. Чем больше интервал усреднения, тем более гладкий вид имеет график скользящих средних. Соседние члены ряда скользящих средних сильно коррелированны, так как в их формировании участвуют одни и те же члены исходного ряда. Это может приводить, к тому, что ряд скользящих средних может содержать циклические компоненты, отсутствующие в исходном ряде. International Sakharov Environmental University 12

Метод скользящего среднего Метод скользящих средних имеет ряд преимуществ перед другими методами: n n n скользящая средняя дает функцию тренда, в наибольшей мере приближенную к значениям исследуемого ряда, поскольку для отдельных частей ряда выбирается наилучшая тенденция; к исследуемому ряду могут быть прибавлены новые значения; нахождение тренда не связано с большими вычислительными трудностями. Недостатком метода скользящей средней является то обстоятельство, что при увеличении периода скольжения теряется информация о крайних периодах ряда, что недопустимо при некоторых приемах анализа временных рядов (например, при спектральном анализе). International Sakharov Environmental University 13

Оценка сезонных компонент в ряде содержащем тренд и циклическую компоненты При наличии во временном ряде тренда, сезонной и циклической компоненты В этом случае, для выделения сезонной компоненты, сначала с помощью метода скользящих средних, совместно оценивается тренд и циклическая компонента. Если скользящее среднее с периодом p, построенное по исходному временному ряду , то для каждого сезона i, рассматриваются все относящиеся к нему разности: International Sakharov Environmental University 14

Оценка сезонных компонент в ряде содержащем тренд и циклическую компоненты Каждое из этих отклонений от можно рассматривать как результат влияния сезонных изменений. Усреднение этих разностей дает оценку сезонной компоненты . В качестве простейшей оценки можно взять среднее арифметическое: International Sakharov Environmental University 15

Метод экспоненциального сглаживания Одной из разновидностей метода усреднения является метод экспоненциального сглаживания. Отличается он тем, что ряд коэффициентов здесь выбирается совершенно определенным образом — их величина падает по экспоненциальному закону. Пусть мы делаем прогноз на момент времени t+1 (на следующий период). Обозначим его как Здесь мы берем в качестве основы прогноза прогноз последнего периода, и добавляем поправку, связанную с ошибкой этого прогноза. Вес этой поправки будет определять, насколько «резко» наша модель будет реагировать на изменения. Очевидно, что Считается, что для медленно меняющегося ряда лучше брать значение 0. 1, а для быстро меняющегося — подбирать в районе 0. 3 0. 5. International Sakharov Environmental University 16

Метод экспоненциального сглаживания Если переписать эту формулу в другом виде, получается Мы получили так называемое рекуррентное соотношение — когда последующий член выражается через предыдущий. Теперь мы прогноз прошлого периода выражаем тем же способом через позапрошлое значение ряда и так далее. В итоге удается получить формулу прогноза International Sakharov Environmental University 17

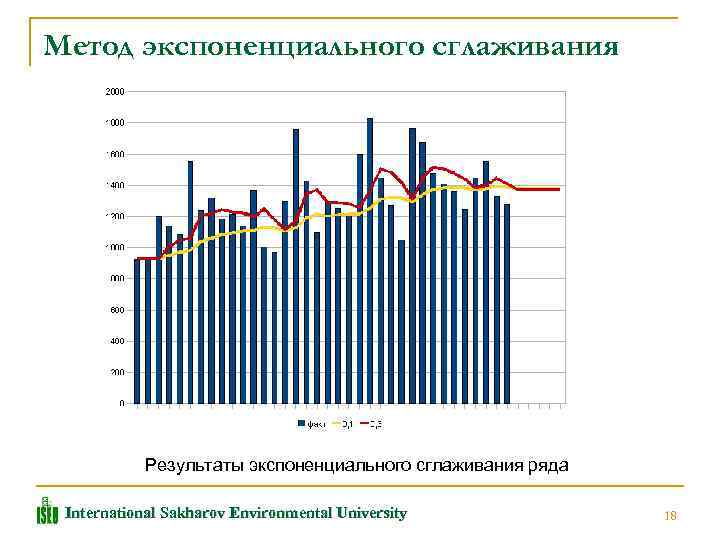Метод экспоненциального сглаживания Результаты экспоненциального сглаживания ряда International Sakharov Environmental University 18

Частотная фильтрация используется для выделения во временном ряду определенных частотных составляющих. Метод возник из технических приложений и предназначался для выделения из данных полезного сигнала, при условии, что известен частотный диапазон сигнала. Фильтр принимает на вход временной ряд и ослабевает определенный диапазон частот временного ряда. Частотная характеристика фильтра определяет, насколько и какие именно частоты он ослабляет. International Sakharov Environmental University 19

Частотная фильтрация При частотной фильтрации выделяют четыре типа фильтров: n n фильтр низких частот пропускает все составляющие с частотами, меньшими заданной, и удаляет из ряда все колебания с большими частотами фильтр высоких частот противоположен фильтру низких и выделяет в качестве полезного сигнала все составляющие с частотами, большими заданной полосно пропускающий фильтр характеризуется двумя частотами и выделяет в качестве сигнала все составляющие с частотами в заданной полосе полосно заграждающий фильтр обратен полосно пропускающему и удаляет из ряда все колебания, частоты которых лежат в заданном диапазоне International Sakharov Environmental University 20

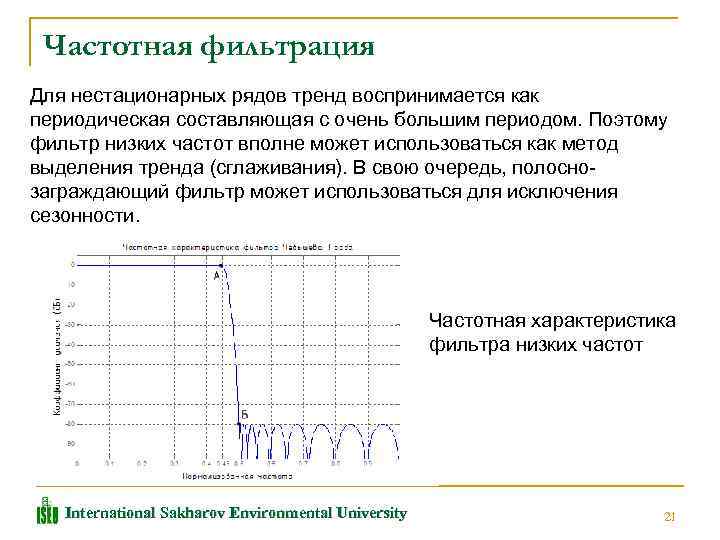Частотная фильтрация Для нестационарных рядов тренд воспринимается как периодическая составляющая с очень большим периодом. Поэтому фильтр низких частот вполне может использоваться как метод выделения тренда (сглаживания). В свою очередь, полосно заграждающий фильтр может использоваться для исключения сезонности. Частотная характеристика фильтра низких частот International Sakharov Environmental University 21

Частотная фильтрация Процесс фильтрации дискретного временного ряда заключается в вычислении значений нового временного ряда в соответствии с выражением: Это выражение называют уравнением линейной дискретной свертки функции x(k) с оператором bn. Интервал суммирования по n получил название "окна" фильтра. Окно фильтра составляет N+1 отсчет. International Sakharov Environmental University 22

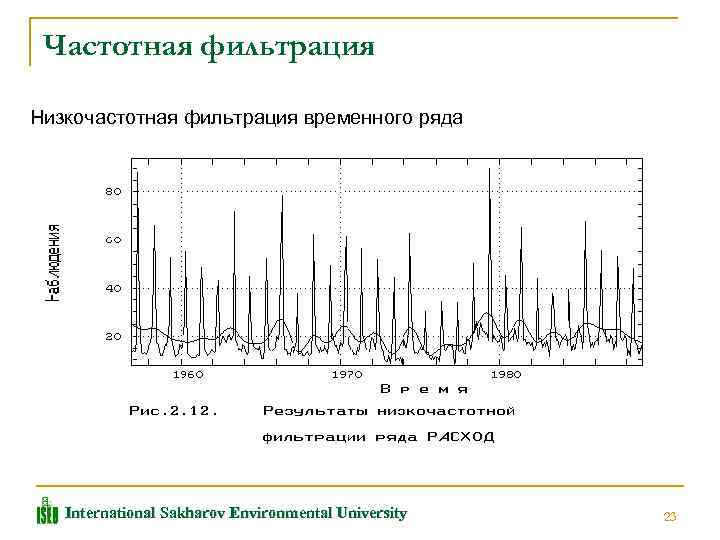Частотная фильтрация Низкочастотная фильтрация временного ряда International Sakharov Environmental University 23

Спектральный анализ В спектральном анализе исследуются периодические модели данных. Цель анализа разложить комплексные временные ряды с циклическими компонентами на несколько основных синусоидальных функций с определенной длиной волн. В результате успешного анализа можно обнаружить всего несколько повторяющихся циклов различной длины в интересующих вас временных рядах, которые, на первый взгляд, выглядят как случайный шум. Наиболее известный пример применения спектрального анализа – исследование циклической природы солнечных пятен: установлена, что активность солнечных пятен имеет 11 ти летний цикл. Часто используются для анализа небесных явлений, изменения погоды, колебания в товарных ценах и т. д. International Sakharov Environmental University 24

Спектральный анализ В отличие от метода выделения сезонных компонент или методов сглаживания, цель спектрального анализа распознать сезонные колебания различной длины, в то время как в предшествующих типах анализа, длина сезонных компонент обычно известна (или предполагается) заранее и затем включается в некоторые теоретические модели. Длина волны функций синуса или косинуса, как правило, выражается числом циклов (периодов) в единицу времени (частота). Период (T) функций синуса или косинуса определяется как продолжительность по времени полного цикла. Таким образом, это обратная величина к частоте: T = 1/f. International Sakharov Environmental University 25

Спектральный анализ Например, временной ряд, состоящий из количества писем, обрабатываемых почтой, может иметь 12 циклов в году. Первого числа каждого месяца отправляется большое количество корреспонденции (много счетов приходит именно первого числа каждого месяца); затем, к середине месяца, количество корреспонденции уменьшается; и затем вновь возрастает к концу месяца. Поэтому каждый месяц колебания в количестве корреспонденции, обрабатываемой почтовым отделением, будут проходить полный цикл. Таким образом, если единица анализа один год, то будет иметь место 12 циклов. При этом могут быть и другие циклы с различными частотами. Например, годичные циклы (=1) и, возможно, недельные циклы (=52 недели в год). Математической основой, которая связывает временной сигнал с его представлением в частотной области, является преобразование Фурье. International Sakharov Environmental University 26

Спектральный анализ Для дискретного временного ряда прямое и обратное преобразования Фурье имеют вид: International Sakharov Environmental University 27

Спектральный анализ Рассмотрим временной ряд из 16 наблюдений, полученных из уравнения: Этот временной ряд состоит из двух основных периодичностей первая с частотой = 0. 0625 (или периодом 1/ 0. 0625 =16; одно наблюдение составляет 1/16 ю длины полного цикла, или весь цикл содержит каждые 16 наблюдений) и вторая с частотой =0. 2 (или периодом 5). Коэффициент при косинусе (1. 0) больше чем коэффициент при синусе (0. 75). Рассмотрим, как с помощью спектрального анализа можно извлечь информацию из этого временного ряда. International Sakharov Environmental University 28

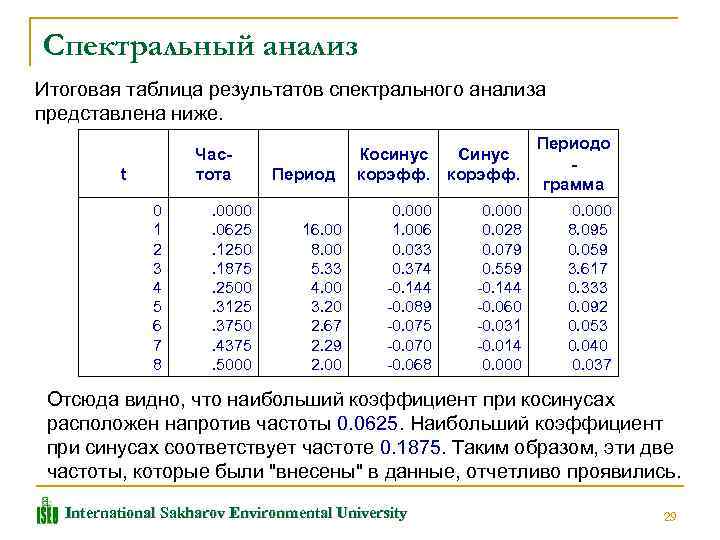Спектральный анализ Итоговая таблица результатов спектрального анализа представлена ниже. t Частота 0 1 2 3 4 5 6 7 8 . 0000. 0625. 1250. 1875. 2500. 3125. 3750. 4375. 5000 Период 16. 00 8. 00 5. 33 4. 00 3. 20 2. 67 2. 29 2. 00 Косинус Синус корэфф. 0. 000 1. 006 0. 033 0. 374 0. 144 0. 089 0. 075 0. 070 0. 068 0. 000 0. 028 0. 079 0. 559 0. 144 0. 060 0. 031 0. 014 0. 000 Периодо грамма 0. 000 8. 095 0. 059 3. 617 0. 333 0. 092 0. 053 0. 040 0. 037 Отсюда видно, что наибольший коэффициент при косинусах расположен напротив частоты 0. 0625. Наибольший коэффициент при синусах соответствует частоте 0. 1875. Таким образом, эти две частоты, которые были "внесены" в данные, отчетливо проявились. International Sakharov Environmental University 29

Спектральный анализ. Периодограмма Функции синусов и косинусов независимы (или ортогональны). Поэтому можно просуммировать квадраты коэффициентов для каждой частоты, чтобы вычислить периодограмму. Более часто, значения периодограммы вычисляются как: Pk = (синус-коэффициентk 2 + косинус-коэффициентk 2 )N/2 где Pk значения периодограммы на частоте fk , и N общая длина ряда. International Sakharov Environmental University 30

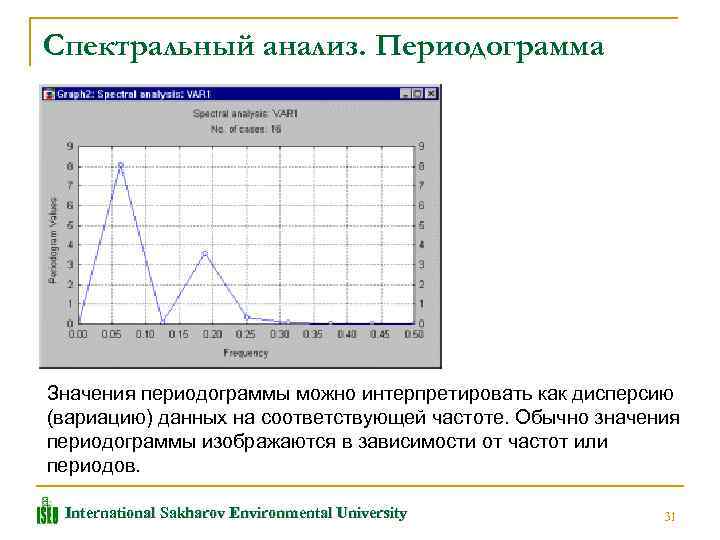Спектральный анализ. Периодограмма Значения периодограммы можно интерпретировать как дисперсию (вариацию) данных на соответствующей частоте. Обычно значения периодограммы изображаются в зависимости от частот или периодов. International Sakharov Environmental University 31

Спектральный анализ. Проблема рассеяния В рассмотренном примере функция синуса с частотой 0. 2 была "вставлена" в ряд. Однако из за того, что длина ряда равна 16, ни одна из частот, полученных в таблице результатов, не совпадает в точности с этой частотой. На практике в этих случаях часто оказывается, что соответствующая частота "рассеивается" на близкие частоты. Например, могут быть найдены большие значения периодограммы для двух близких частот, когда в действительности существует только одна основная функция синуса или косинуса с частотой, которая попадает на одну из этих частот или лежит между найденными частотами. International Sakharov Environmental University 32

Спектральный анализ. Проблема рассеяния Существует три подхода к решению проблемы рассеяния: n n n При помощи добавление констант во временной ряд можно увеличить количество вычисляемых частот Применяя сглаживание ряда перед анализом, можно уменьшить рассеяние Применяя сглаживание периодограммы, можно идентифицировать основные частотные области или (спектральные плотности), которые существенно влияют на циклическое поведение ряда International Sakharov Environmental University 33

Спектральный анализ. Проблема рассеяния 1. Так как частотные величины вычисляются как N/t, можно просто добавить в ряд константы (например, нули), и таким образом получить увеличение частот. 2. Так называемый процесс косинус-сглаживания рекомендуемое преобразование ряда, предшествующее спектральному анализу. Оно обычно приводит к уменьшению рассеяния в периодограмме. Его суть заключается в преобразовании данных в начале и в конце ряда при помощи умножения на веса: для t=0 до m 1 для t=N m до N 1 International Sakharov Environmental University 34

Спектральный анализ. Проблема рассеяния 3. На практике, при анализе данных обычно не очень важно точно определить частоты основных функций синусов или косинусов. Скорее, т. к. значения периодограммы объект существенного случайного колебания, можно столкнуться с проблемой многих хаотических пиков периодограммы. В этом случае хотелось бы найти частоты с большими спектральными плотностями, т. е. частотные области, состоящие из многих близких частот, которые вносят наибольший вклад в периодическое поведение всего ряда. Это может быть достигнуто путем сглаживания значений периодограммы с помощью преобразования взвешенного скользящего среднего. Для вычисления весов взвешенного скользящего среднего значений периодограммы наиболее распространены подходы: Парзена, Даниэля, Тьюки, Хемминга и т. д. International Sakharov Environmental University 35

Кросс-спектральный анализ Кросс спектральный анализ позволяет анализировать одновременно два ряда. Рассмотрим два временных ряда в которых присутствуют две существенных синхронных периодичности с частотами 0. 0625 и 0. 1875: International Sakharov Environmental University 36

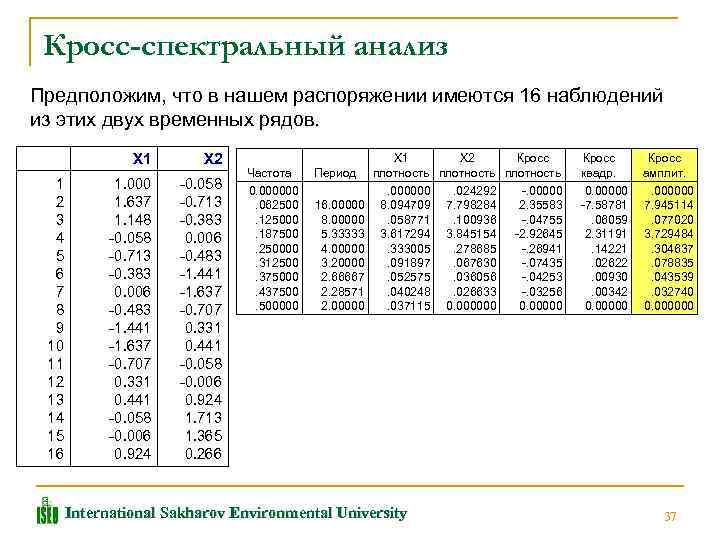Кросс-спектральный анализ Предположим, что в нашем распоряжении имеются 16 наблюдений из этих двух временных рядов. X 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 X 2 1. 000 1. 637 1. 148 0. 058 0. 713 0. 383 0. 006 0. 483 1. 441 1. 637 0. 707 0. 331 0. 441 0. 058 0. 006 0. 924 1. 713 1. 365 0. 266 Частота Период 0. 000000. 062500. 125000. 187500. 250000. 312500. 375000. 437500. 500000 16. 00000 8. 00000 5. 33333 4. 00000 3. 20000 2. 66667 2. 28571 2. 00000 X 1 X 2 Кросс плотность. 000000 8. 094709. 058771 3. 617294. 333005. 091897. 052575. 040248. 037115 International Sakharov Environmental University . 024292 7. 798284. 100936 3. 845154. 278685. 067630. 036056. 026633 0. 000000 2. 35583 . 04755 2. 92645 . 26941 . 07435 . 04253 . 03256 0. 00000 Кросс квадр. Кросс амплит. 0. 00000 7. 58781. 06059 2. 31191. 14221. 02622. 00930. 00342 0. 000000 7. 945114. 077020 3. 729484. 304637. 078835. 043539. 032740 0. 000000 37

Анализ коррелограмм. Автокорреляционная функция Образуем из временного ряда x 1, x 2, …, xn совокупность из n 1 пар: (x 1, x 2), (x 2, x 3), …, (xn, xn 1). Первый элемент каждой пары будем рассматривать как случайную величину Xt, а второй – как случайную величину Xt+1. Тогда оценка коэффициента корреляции между Xt и Xt+1 (с учетом определенных допущений) может быть записана в виде: International Sakharov Environmental University 38

Анализ коррелограмм. Автокорреляционная функция Аналогичным образом может быть оценена корреляция между Xt, и Xt+k: Функцию rk аргумента k при k=1, 2, … называют автокорреляционной функцией. График автокорреляционной функции называют коррелограммой. International Sakharov Environmental University 39

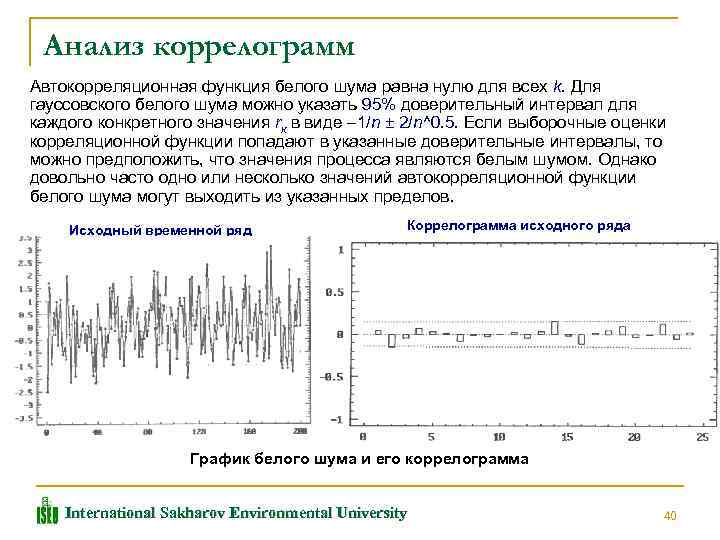Анализ коррелограмм Автокорреляционная функция белого шума равна нулю для всех k. Для гауссовского белого шума можно указать 95% доверительный интервал для каждого конкретного значения rк в виде – 1/n ± 2/n^0. 5. Если выборочные оценки корреляционной функции попадают в указанные доверительные интервалы, то можно предположить, что значения процесса являются белым шумом. Однако довольно часто одно или несколько значений автокорреляционной функции белого шума могут выходить из указанных пределов. Исходный временной ряд Коррелограмма исходного ряда График белого шума и его коррелограмма International Sakharov Environmental University 40

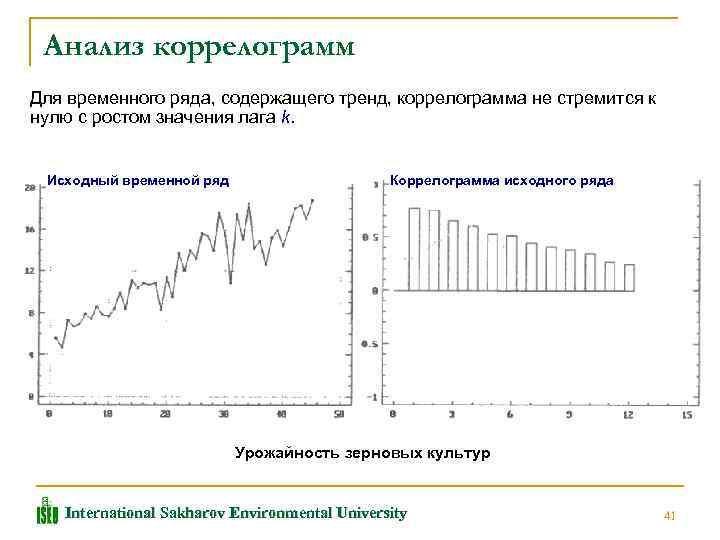Анализ коррелограмм Для временного ряда, содержащего тренд, коррелограмма не стремится к нулю с ростом значения лага k. Исходный временной ряд Коррелограмма исходного ряда Урожайность зерновых культур International Sakharov Environmental University 41

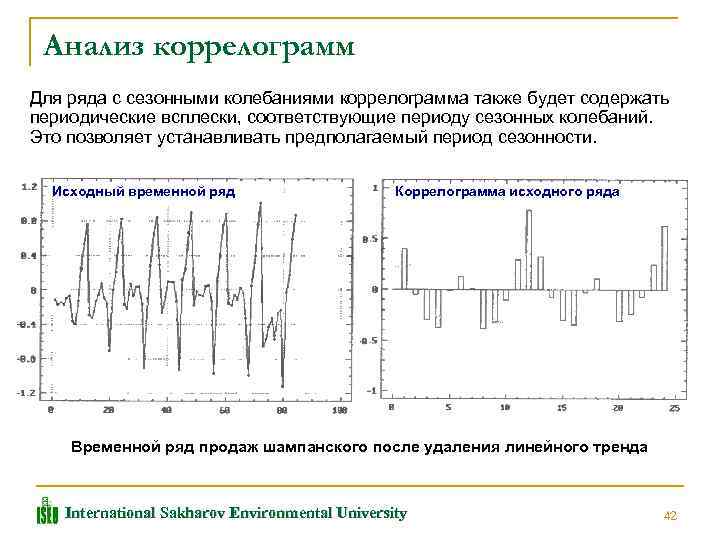Анализ коррелограмм Для ряда с сезонными колебаниями коррелограмма также будет содержать периодические всплески, соответствующие периоду сезонных колебаний. Это позволяет устанавливать предполагаемый период сезонности. Исходный временной ряд Коррелограмма исходного ряда Временной ряд продаж шампанского после удаления линейного тренда International Sakharov Environmental University 42

Критерий Дарбина-Уотсона Критерий Дарбина Уотсона представляет собой распространенную статистику, предназначенную для тестирования наличия автокорреляции остатков первого порядка после сглаживания ряда или в регрессионных моделях. Численное значение коэффициента равно d = [(e(2) e(1))2 +. . . + (e(n) e(n 1))2]/[e(1)2 +. . . + e(n)2] где e(t) остатки. Возможные значения критерия находятся в интервале от 0 до 4. Если значение d близко к 2 следовательно автокорреляция отсутствует. Меньшие значения соответствуют положительной автокорреляции остатков, большие отрицательной. International Sakharov Environmental University 43

Стохастические модели временных рядов Идея использования математических моделей для описания поведения физических объектов является общепризнанной. В частности, иногда удается получить модель, основанную на физических законах, что дает возможность вычислить почти точное значение какой либо зависящей от времени величины в любой момент времени. Такие модели называются детерминированными, хотя реальные объекты крайне редко бывают целиком детерминированными. Поэтому в случае экологических объектов, для которых доля влияния случайных (неучитываемых) факторов традиционно очень велика, можно предложить модели, позволяющие вычислить лишь вероятность того, что некоторое будущее значение будет лежать в определенном интервале. Такие модели называются вероятностными, либо стохастическими. Интервал времени, на который существует необходимость прогноза вперед при решении конкретной проблемы, называется периодом упреждения. International Sakharov Environmental University 44

Стохастические модели временных рядов Пусть x(t + l) измеренное значение экологического показателя в момент времени t с упреждением на будущее l. Функция φt(l), l = 1, 2, . . . , дающая в момент t прогнозы для всех будущих времен упреждения, будет называться прогнозирующей функцией в момент t. Очевидна цель получить такую прогнозирующую функцию, у которой среднее значение квадрата отклонения истинного значения от прогнозируемого [x(t + l) φt (l)]2 является наименьшим для каждого упреждения l. В дополнение к вычислению наилучшего прогноза необходимо также указать его точность, чтобы можно было оценить риск, связанный с решениями, основанными на прогнозировании. Точность прогноза выражается, как правило, доверительными пределами по обе стороны от прогнозируемых значений для любого удобного значения уровня вероятности h (например, для 95%). International Sakharov Environmental University 45

Стохастические модели временных рядов Простые параметрические модели тренда не всегда обеспечивают эффективное вычисление будущего поведения объектов. Определенной альтернативой являются итеративные модели, основанные на концепции того, что временные ряды, в которых наблюдается отчетливая автокорреляция, целесообразно рассматривать как результат некоторого преобразования последовательности независимых импульсов at. Эти импульсы реализация случайных величин с фиксированным распределением, которое обычно предполагается нормальным с нулевым средним и дисперсией s a 2, что соответствует "белому шуму". International Sakharov Environmental University 46

Стохастические модели временных рядов Считается, что "белый шум" at можно трансформировать в традиционно рассматриваемый стационарный процесс, используя следующие преобразования: n фильтр авторегрессии (АР), в котором текущее значение процесса yt выражается в виде конечной линейной совокупности предыдущих значений процесса yt-1, yt-2, . . . плюс случайный импульс at n фильтр скользящего среднего (СС), в котором процесс yt образуется из белого шума at как взвешенная сумма предыдущей последовательности импульсов at, at 1, at 2. . . International Sakharov Environmental University 47

Стохастические модели временных рядов Современная статистическая теория оценивания параметров таких моделей была развита Дж. Боксом и Г. Дженкинсом. Модели АР и СС достаточно высокого порядка могут хорошо аппроксимировать почти любой стационарный процесс. В связи с этим модель АР часто применяется для моделирования остатков в той или иной параметрической модели, например регрессионной модели или модели тренда. Для достижения большей гибкости в подгонке модели к наблюдаемым временным рядам часто целесообразно объединить в одной модели оба преобразования, получив комбинированную модель авторегрессии скользящего среднего (АРСС). Уравнения АР и СС могут быть вычислены и для нестационарных процессов (особенно, если нестационарность носит однородный характер). Однако более эффективна для описания как стационарных, так и нестационарных рядов со стационарными приращениями d го порядка и рациональным спектром комбинированная модельавторегрессии интегрированного скользящего среднего (АРИСС). International Sakharov Environmental University 48

Этапы построения стохастических моделей временных рядов Дж. Бокс и Г. Дженкинс предлагают следующие этапы построения моделей динамики для целей прогнозирования или управления: n n постулирование общего класса моделей, когда из теоретических и практических соображений и поставленной цели моделирования выбирается полезное семейство гипотетической модели структурная идентификация конкретных подклассов выбранных типов моделей с использованием статистических характеристик временных рядов (например, на основе анализа графиков автокорреляционной функции и спектра) оценка параметров идентифицированных моделей диагностическая проверка адекватности конкретной модели Если в результате диагностики модели были обнаружены дефекты подгонки, последние три этапа итеративно повторяются. International Sakharov Environmental University 49

Этапы построения стохастических моделей временных рядов Идентификация это процедура определения конкретного типа параметрической модели, поскольку общий класс стохастических моделей слишком обширен для непосредственной подгонки к данным. В моделях АР и СС идентификация заключается в выборе периода упреждения l. Задачей идентификации является и выбор наименьшего возможного числа параметров модели при условии ее достаточной адекватности (принцип экономичности модели ). Например, использование завышенного порядка разности приводит к заметному росту дисперсии прогноза. Очевидно, что процесс идентификации неизбежно неточен, поскольку основывается на "неточных" непараметрических критериях. International Sakharov Environmental University 50

Этапы построения стохастических моделей временных рядов Стохастические модели временных рядов основываются на некотором множестве коэффициентов (параметров), значения которых должны оцениваться по результатам наблюдений. Здесь используются разные по форме оценки целевой функции оптимизации (чаще всего условный или безусловный методы наименьших квадратов). Наиболее популярен для оптимизации целевой функции при построении моделей АР и СС алгоритм Маркварда, причем для нахождения начального приближения используются уравнения Юла-Уокера , связывающие коэффициенты модели с теоретическими значениями АКФ. В процессе нахождения оценок модели может возникать вырождение, которое почти неизбежно, когда порядки авторегресии и скользящего среднего в модели неоправданно велики. Если же в этом случае и не возникнут вычислительные проблемы, то скорее всего часть оцененных параметров не будет значимо отличаться от нуля. International Sakharov Environmental University 51

Этапы построения стохастических моделей временных рядов Если процесс оценивания успешно осуществлен, возникает проблема оценки качества построенной модели. Для "хорошей" модели остатки должны быть "белым шумом", т. е. их выборочные коэффициенты автокорреляции не должны значимо отклоняться от нуля. Кроме того, модель не должна содержать лишних параметров, т. е. желательно уменьшать число параметров, пока не появится значимая автокорреляция остатков. Для диагностики модели необходимо попытаться модифицировать ее, меняя порядки АР и СС. International Sakharov Environmental University 52

Модель авторегрессии В авторегрессионной модели порядка p любое текущее значение процесса yt выражается как конечная линейная совокупность p предыдущих значений процесса и импульса at (уровни ряда регрессируют на своих предыдущих значениях): yt = φ1 yt-1 + φ2 yt-2 +. . . + φ p yt-p + at где yt = xt m. Эта модель содержит p + 2 неизвестных параметра: коэффициенты многочлена φ1 , . . . , φp , "средний уровень" процесса m и дисперсию sa 2 белого шума, которые на практике следует оценить по наблюдениям. International Sakharov Environmental University 53

Модель авторегрессии первого порядка имеет вид : yt = φ1 yt-1 + at Автокорреляционная функция процесса авторегрессии первого порядка вычисляется следующим образом: rk = φ1 k International Sakharov Environmental University 54

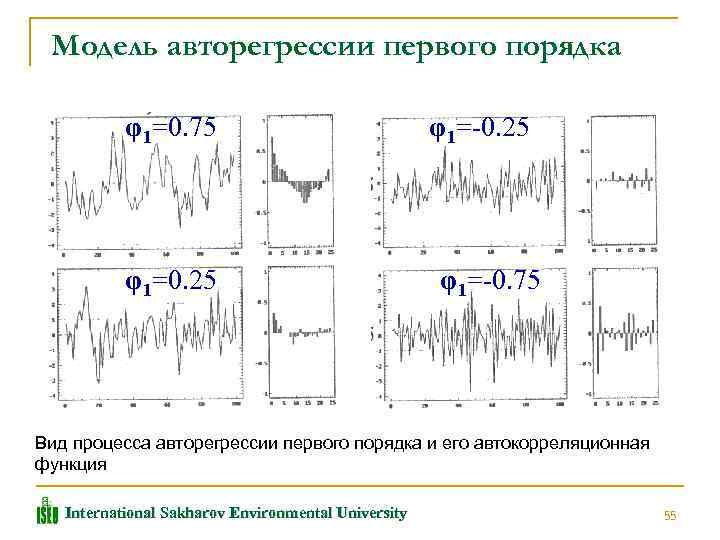Модель авторегрессии первого порядка φ1=0. 75 φ1=0. 25 φ1=-0. 75 Вид процесса авторегрессии первого порядка и его автокорреляционная функция International Sakharov Environmental University 55

Оценивание параметров авторегрессии первого порядка по наблюдениям В качестве оценки m берется среднее по наблюдениям: Из выражения для автокорреляционной функции rk = φ1 k получают оценку параметра φ1: Для оценки дисперсии sa 2 можно воспользоваться выражением для оценки дисперсии стационарного процесса: International Sakharov Environmental University 56

Модель авторегрессии. Оператор сдвига Пусть u и υ две последовательности Тогда последовательность υ можно получить из последовательности u путем действия на u оператора сдвига B: если ut = υt-1 для всякого целого t. International Sakharov Environmental University 57

Модель авторегрессии. Оператор сдвига Можно определить степени оператора сдвига B: Это означает, что если υ=B 2 u то для всякого целого t: ut = υt-2 Можно ввести оператор представляющий собой многочлен от B. Пусть По определению, υ=P(B)u если International Sakharov Environmental University 58

Модель авторегрессии Тогда с помощью многочлена от B процесс авторегрессии можно представить в виде: P(B) yt = at При этом процесс yt стационарен, если все корни полинома P (B) = 1 φ1 B φ2 B 2 . . . φ p Bp лежат внутри единичного круга |y| < 1. При слабых дополнительных предположениях стационарный процесс удовлетворяет уравнению авторегрессии бесконечного порядка, с достаточно быстро убывающими коэффициентами. International Sakharov Environmental University 59

Модель авторегрессии Рассмотрев корреляцию между X(t) и X(t-1) получим выражение для автокорреляционной функции процесса авторегрессии порядка p Тогда для значений k = 1, 2, … p получим систему уравнений Юла Уолкера: Решив эту систему уравнений, получим значения параметров φ1 , …, φp модели авторегрессии порядка p International Sakharov Environmental University 60

Модель скользящего среднего порядка q описывает стационарные процессы как некоторую линейную комбинацию "белого шума" и записывается в виде yt = at θ 1 at 1 θ 2 at 2 . . . θp at -q где yt = xt m. Модель содержит q + 2 неизвестных параметра: коэффициенты многочлена θ 1, . . . , θq; "средний уровень" процесса m и дисперсию sa 2 белого шума, которые на практике следует оценить по наблюдениям. Для теоретического процесса СС(q) все значения автокорреляционной функции для лагов, больших q, равны нулю. International Sakharov Environmental University 61

Модель скользящего среднего С помощью многочлена от B процесс скользящего среднего можно представить в виде: Q(B) yt = at При этом процесс yt стационарен, и все корни полинома Q (B) = 1 θ 1 B θ 2 B 2 . . . θ p Bp лежат внутри единичного круга |y| < 1. Оценивание параметров модели скользящего среднего осуществляется путем минимизации целевой функции, полученной с помощью методов наименьших квадратов. Для нахождения минимума целевой функции используется метод оптимизации Марквардта (алгоритм Левенберга Марквардта). International Sakharov Environmental University 62

Модель Бокса-Дженкинса (АРИСС) Модель АРИСС одну из наиболее популярных моделей для построения краткосрочных прогнозов часто называют по имени авторов, предложивших методику ее применения для временных рядов, некоторая d я разность которых стационарна. Модель зависит от трех структурных целочисленных параметров p, d, q и записывается в виде wt = φ1 wt 1 + φ2 wt 2 +. . . + φpwt p θ 1 at 1 θ 2 at 2 . . . θp at q где at "белый шум"; wt = (Δdxt) m ; Δd оператор взятия разности порядка d, m константа, определяющая средний уровень ряда. Параметры φ являются параметрами авторегрессии, а параметры θ параметрами скользящего среднего. International Sakharov Environmental University 63

Модель Бокса-Дженкинса (АРИСС) Важными специальными классами моделей АРИСС являются: модель авторегрессии скользящего среднего АРСС(p, q) = АРИСС(p, 0, q) yt = y 1 wt 1 + y 2 wt 2 +. . . + ypwt p y 1 at 1 y 2 at 2 . . . yp at q где yt = xt m; d = 0, а также модель ИСС(d, q) = АРИСС(0, d, q), в которой p = 0. Очевидно, что и модель авторегресии АР(p) можно представить как частный случай АРИСС(p, 0, 0), для которой d = q = 0. Другой частный случай модель скользящего среднего СС(q), для которой p = d = 0. International Sakharov Environmental University 64

Модель Бокса-Дженкинса (АРИСС) Первый шаг идентификации моделей АРИСС определение порядка разности d, который должен быть выбран так, чтобы ряд wt = (Δd xt) был стационарным. Для определения d текущие разности ряда последовательно тестируются на стационарность. На практике часто оказывается, что адекватное описание наблюдаемых временных рядов достигается при помощи моделей, в которых p и q не больше 2. Наилучшая модель АРИСС(3, 0, 0) для временного ряда , представляющего собой изменение значений концентраций ионов аммония в Волжском бассейне, полученная перебором всех p, d и q до 3 го порядка, имеет вид xt = 17. 264 + 0. 421 xt 1 + 0. 15 xt 2 + 0. 237 xt 3 International Sakharov Environmental University 65

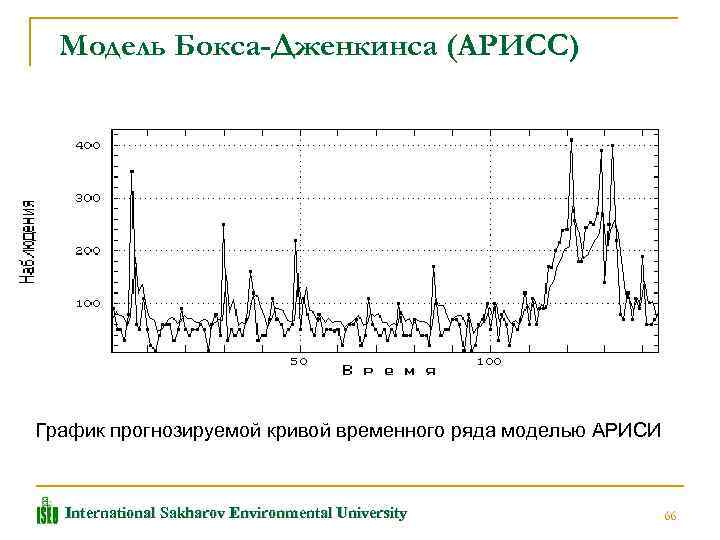Модель Бокса-Дженкинса (АРИСС) График прогнозируемой кривой временного ряда моделью АРИСИ International Sakharov Environmental University 66