Suppression of the quantum-mechanical collapse in quantum gases

Suppression of the quantum-mechanical collapse in quantum gases by repulsive interactions Hidetsugu Sakaguchi Department of Applied Science for Electronics and Materials, Interdisciplinary Graduate School of Engineering Sciences, Kyushu University, Fukuoka, Japan Boris A. Malomed Department of Physical Electronics, Faculty of Engineering, Tel Aviv University, Tel Aviv, Israel

Main results have been published in:

An extension of the analysis:

(1) Introduction and the model The attractive potential ~1/r 2 plays the wellknown critical role in the standard quantum mechanics, leading to the quantum collapse, alias “fall onto the center” in 3 D and 2 D geometries. The scaled form of the Schrödinger equation with this potential (the harmonic trapping potential, Ω²r ²/2, is included too) is

The corresponding classical Hamiltonian is scale-invariant, H(r → ar) = H(r)/a 2 (in other words, all values of U 0 lead to the same classical dynamics). However, the quantization destroys this classical invariance (which is known as the “quantum anomaly”).

As a result, the 3 D Schrödinger equation with potential -1/r 2 has no ground state for U 0 > ¼, and does have it at U 0 < ¼. The 2 D Schrödinger equation has no ground state for any U 0 > 0. This phenomenon of the quantum collapse are also called “fall onto the center” in the book Quantum Mechanics by Landau and Lifshitz.

The physical interpretation of both the 3 D and 2 D Schrödinger equations with this potential: the interaction between a particle carrying a permanent electric dipole moment d, and an electric charge Q placed at the origin. If the orientation of the moment is locked to the local electric field (E), the effective interaction potential is precisely -(1/2)U 0/r 2, with U 0 = 2|Q|d :

In particular, if Q = 1 is the electron’s charge, and the mass of the particle is taken as ~ 10 proton masses, the critical value of the attraction strength U 0 = ¼, corresponds, in physical units, to a very small value of the dipole moment, d ~ 10 -5 Debye, hence the case of U 0 > ¼ is essential indeed.

In the experiment, a relevant combined trap, which can simultaneously hold a gas of ultra-cold bosons and a charged ion at the center, is available: Dynamics of a Cold Trapped Ion in a Bose-Einstein Condensate, S. Schmid, A. Härter, and J. H. Denschlag, Phys. Rev. Lett. 105, 133202 (2010).

In the 2 D geometry (which corresponds to a pancake-shaped BEC configuration), another interpretation is possible too, in addition to the above-mentioned one: the interaction of a particle carrying a magnetic dipole moment with a current filament which transversely intersects the 2 D layer, assuming that the orientation of the magnetic moment is locked to the local magnetic field induced by the current.

A solution to the quantum anomaly problem in this quantum-mechanical setting (i. e. , the nonexistence of the ground state) was proposed outside of the framework of quantum mechanics – in terms of the linear quantum-field theory. Essentially, that solution postulates that the ground state is created by the field-theory renormalization procedure. The so created ground state features an arbitrary spatial scale imposed by the renormalization: K. S. Gupta and S. G. Rajeev, Phys. Rev. D 48, 5940 (1993); H. E. Camblong, L. N. Epele, H. Fanchiotti, and C. A. Garcia Canal, Phys. Rev. Lett. 85, 1590 (2000).

Our objective is to propose a different solution of the quantum-collapse problem: taking into account, in the mean -field approximation, collisions between dipolar particles attracted to the center by the potential -1/r 2, i. e. , replacing the Schrödinger equation by the corresponding Gross-Pitaevskii equation. This approach will create a ground state, with the spatial scale uniquely determined by physical parameters of the system.

The corresponding Gross-Pitaevskii equation, with the contact repulsive nonlinearity: The realization of ultracold quantum gases formed by molecules carrying electric dipole moments may be possible, using (for instance) Li-Cs bosonic molecules: J. Deiglmayr, A. Grochola, M. Repp, K. Mörtlbauer, C. Glück, J. Lange, O. Dulieu, R. Wester, and M. Weidemüller, Phys. Rev. Lett. 101, 133004 (2008).

For the 2 D realization (with the transverse current filament), the quantum gas (BEC) of Cr 52 atoms carrying magnetic moments is available too: A. Griesmaier, J. Werner, S. Hensler, J. Stuhler and T. Pfau, Phys. Rev. Lett. 94, 160401 (2005); Q. Beaufils, R. Chicireanu, T. Zanon, B. Laburthe-Tolra, E. Marechal, L. Vernac, J. C. Keller, and O. Gorceix, Phys. Rev. A 77, 061601(R) (2008).

Recently, the creation of BEC was also reported in the atomic gas of dysprosium, which has the largest magnetic moment among all chemical elements: M. Lu, N. Q. Burdick, S. H. Youn, and B. L. Lev, Phys. Rev. Lett. 107, 190401 (2011). Another “magnetic” realization of the 2 D setting may be possible in gas of magnetic -dipolar molecules of (Rb 87)2: F. Lang, K. Winkler, C. Strauss, R. Grimm, and J. H. Denschlag, Phys. Rev. Lett. 101, 133005 (2008).

Taking into account the dipole-dipole interactions in the Gross-Pitaevskii equation:

For m ~ 10 proton masses and as ~ 10 nm, the renormalization of the scattering length is essential for d ~ 1 Debye.

(2) Presentation of results (i) The standard description of the quantum collapse will be recapitulated. (ii) In the 3 D case, it will be demonstrated that the repulsive cubic nonlinearity suppresses the quantum collapse, i. e. , it creates the ground state which is missing in the linear Schrödinger equation. (iii) It will also be demonstrated that, in cases when the potential -(1/2)U 0/r 2 is not strong enough to cause the quantum collapse in 3 D, the action of the cubic nonlinearity in the combination with the harmonic trapping potential gives rise to a tri-stability of bound states.

(iv) It will be shown that the cubic nonlinearity is insufficiently strong to suppress the quantum collapse in the 2 D setting. However, the quintic nonlinearity does it. (v) It will be demonstrated (in a brief form) that the nonlinearity also suppresses the quantum collapse and creates the missing ground state in the case when a strong external uniform polarizing field reduces the symmetry of the 3 D setting from spherical to cylindrical.

(i) Recapitulation of the description of the quantum collapse in the linear Schrödinger equation Solutions to the 3 D and 2 D linear Schrödinger equations (including the harmonic trap), with angular momentum ℓ, are sought for as, respectively,

(ii) The suppression of the quantum collapse by the repulsive cubic nonlinearity in 3 D (no harmonic trap, Ω = 0).

Using this approximation, one can calculate the norm of the solution, N, and thus derive an approximate μ(N) characteristic for the ground state:

The family of the ground-state solutions was then found in a numerical form, as a solution of the radial equation for the 3 D wave function. The solutions, both analytical and numerical, exist equally well for U 0 < ¼ and U 0 > ¼, i. e. , in cases when the linear Schrödinger equation does and does not have the ground state. Numerical simulations confirm that all the ground states are stable. Note that, in the absence of the external trap (Ω = 0), the ground state generated by the linear equation with U 0 < ¼ is unnormalizable (at r → ∞), but its norm is finite in the case of the nonlinear equation.

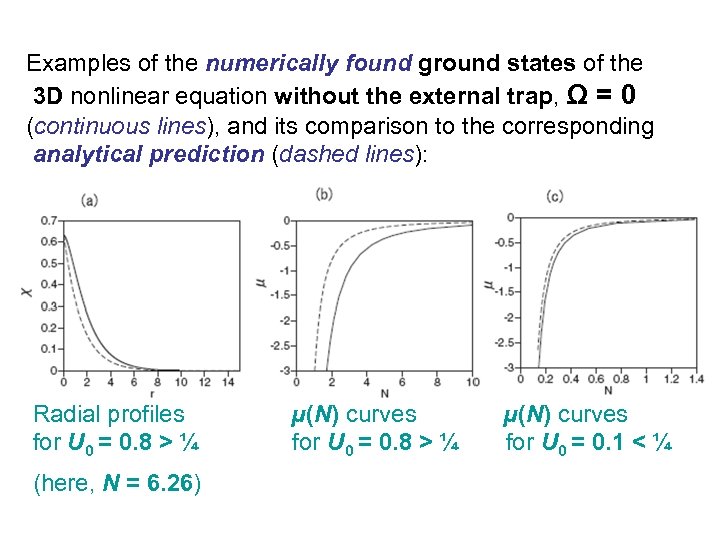Examples of the numerically found ground states of the 3 D nonlinear equation without the external trap, Ω = 0 (continuous lines), and its comparison to the corresponding analytical prediction (dashed lines): Radial profiles for U 0 = 0. 8 > ¼ (here, N = 6. 26) μ(N) curves for U 0 = 0. 8 > ¼ μ(N) curves for U 0 = 0. 1 < ¼

(iii) The effect of the additional harmonic trapping potential (Ω² > 0) in the 3 D case The harmonic trap (Ω² > 0) distorts the branch of the ground states which was created by the nonlinearity, and additionally supports extensions of the two bound modes that were found in the exact form as solutions to the linear Schrödinger equation with Ω² > 0. As well as in the case of the linear equation, these additional modes exist precisely at U 0 < ¼ (where the linear equation does not give rise to the quantum collapse). The two additional modes were shown (by dint of direct simulations) to be stable. Thus, the nonlinear equation gives rise to the tri-stability at U 0 < ¼.

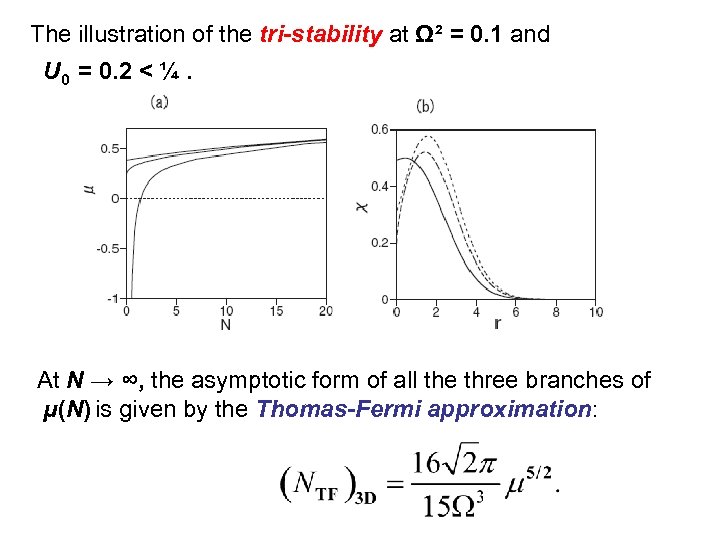The illustration of the tri-stability at Ω² = 0. 1 and U 0 = 0. 2 < ¼. At N → ∞, the asymptotic form of all the three branches of μ(N) is given by the Thomas-Fermi approximation:

(iv) The suppression of the quantum collapse in the 2 D setting by the quintic repulsive term In the 2 D situation, the cubic repulsive term formally gives rise to the wave function, which replaces the collapsing ne, with the asymptotic form ~ 1/r at r → 0 (the same as in 3 D). However, unlike the 3 D case, the norm of such a wave function diverges at r → 0 in 2 D, i. e. , the cubic term is not strong enough to create the missing 2 D ground state.

The suppression of the 2 D quantum collapse may be provided by a quintic term, which may account for (elastic) triple collisions in the quantum gas: F. K. Abdullaev, A. Gammal, L. Tomio, and T. Frederico, Phys. Rev. A 63, 043604 (2001).

Note that the vortex-carrying solution usually requires ψ = 0 at the pivot, lest the phase of the wave function (with ψ ≠ 0 at the pivot) should be non-uniquely defined at the central point. In the present situation, this problem is avoided in the opposite way: the wave function at the pivot diverges, as ψ ~ r -1/2. For the wave function with |ψ| = ∞, the phase does not need to be uniquely defined, as well as for | ψ | = 0.

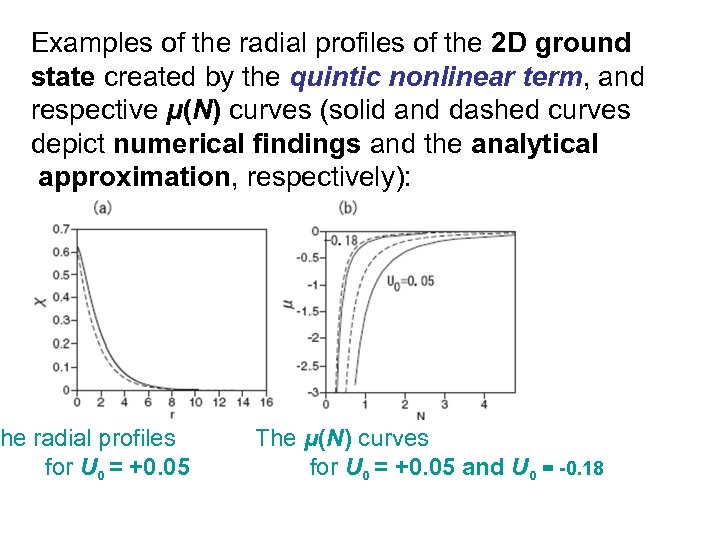Examples of the radial profiles of the 2 D ground state created by the quintic nonlinear term, and respective μ(N) curves (solid and dashed curves depict numerical findings and the analytical approximation, respectively): he radial profiles for U 0 = +0. 05 The μ(N) curves for U 0 = +0. 05 and U 0 = -0. 18

Note that the quintic nonlinearity also supports the ground state with the finite norm at - ¼ < U 0 < 0 (which corresponds to the weakly repulsive central potential). However, exactly at U 0 = 0, the entire solution vanishes, ψ ≡ 0. Indeed, in the free space (no potential at all), the selfrepulsive nonlinearity cannot support any localized mode. Direct simulations verify that the 2 D ground states are stable.

The effect of the additional harmonic trapping potential (Ω² > 0) in the 2 D case In the case of - ¼ < U 0 < 0 , the addition of the harmonic trap to the 2 D quintic equation creates two extra bound states, which represent the nonlinear deformation of the two eigenstates which were found as exact solutions to the linear 2 D Schrödinger equation. There also remains the ground state created by the quintic nonlinearity, which is distorted by the harmonic potential, Ω²r²/2.

The difference from the tri-stability, which was reported in the 3 D case in the presence of the harmonic trap, is that, in the 2 D case, the intermediate branch of μ(N) represents an unstable state, which spontaneously transforms itself into a robust breather: An example of the unstable confined mode transforming into the her with the oscillating amplitude is presented here for U 0 = -0. 18 and Ω² = 0. 10. The limit form of the bottom and upper branches at N → ∞ is again given by the Thomas-Fermi approximation:

(v) The anisotropic extension of the 3 D setting: If the local orientation of the electric dipoles is frozen into a strong external uniform field, the symmetry of the potential of the interaction of the dipoles with the central electric charge is reduced from spherical to cylindrical, U(r , θ) = -(U 0/2)r -²cosθ, where θ is the angular coordinate in 3 D. The cylindrically-symmetric 3 D ground-state wave function is created by the nonlinearity in this case too: H. Sakaguchi and B. A. Malomed, Phys. Rev. A 84, 033616 (2011).

(3) CONCLUSIONS (i) The problem of the “fall onto the center/quantum collapse/quantum anomaly”, induced by the attractive potential –U 0/r ² in 3 D and 2 D settings, can be resolved by the repulsive cubic (in 3 D) or quintic (in 2 D) terms, which are added to the respective linear Schrödinger equation, transforming it into the Gross-Pitaevskii equation. The nonlinear term creates the stable ground state, which was absent in the linear equation. The spatial scale of the newly created ground state is uniquely determined by physical parameters of the system, rather than being arbitrarily imposed by the quantum-field renormalization procedure, as proposed in earlier works on this topic. These 3 D and 2 D models may be realized as BEC of molecules or atoms composed of dipolar molecules or atoms.

(ii) The newly created ground states are relevant also in the case when the linear Schrödinger equation does not give rise to the collapse (for instance, at U 0 < ¼ in the 3 D case), as the corresponding solution to the linear equation is unnormalizable, while the norm of the ground state created by the nonlinear equation is always finite. (iii) In the case when the linear equation does not yet give rise to the collapse, and the harmonic trapping potential is added, the corresponding nonlinear equation gives rise to the tri-stability of the bound states in the 3 D case, and to bi-stability in the 2 D case, with an additional intermediate branch of unstable states in the 2 D case, which spontaneously transform into robust breathers.

(4) The ground state is created as well by the selfrepulsive nonlinearity in the 3 D model with the symmetry reduced from spherical to cylindrical by the strong external uniform field, which polarizes the dipole moments of the particles.

(4) PROSPECTIVE EXTENSIONS (i) In the 3 D case, it is interesting to extend the analysis of the nonlinear equation for the vortical modes carrying the angular momentum. (ii) It may also be interested to consider the 3 D problem for the setting with two attractive centers, and (on the other hand) for a two-component quantum gas. (iii) A challenging issue is to extend the analysis to the quantum gas of fermionic particles.