СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СВЯЗИ МЕЖДУ ПРИЗНАКАМИ 1. Виды связей,

СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СВЯЗИ МЕЖДУ ПРИЗНАКАМИ 1. Виды связей, методы их изучения 2. Метод аналитической группировки 3. Показатели силы и тесноты связи на основе аналитической группировки 4. Основы корреляционно-регрессионного анализа

Виды связей • Функциональные или жестко детерминированные • Стохастические или статистические

Виды связей (по общему направлению факторного и результативного признаков) • Прямые связи — направление изменения факторного и результативного признаков совпадает • Обратные связи — направление изменения факторного и результативного признаков не совпадает

Виды связей (по форме связи ) • Линейные • Нелинейные

Методы измерения связей • Прямые (балансовый метод, индексный метод) • Косвенные основаны на соответствии вариации значений факторного и результативного признаков

Косвенные методы измерения взаимосвязей • Метод аналитической группировки • Корреляционно-регрессионный анализ

Метод аналитической группировки • Единицы совокупности объединяются в группы по значению факторного признака • По каждой выделенной группе рассчитываются средне значения результативного признака • Через сопоставление изменения факторного и результативного признаков делается предположение о наличии или отсутствии связи между признаками

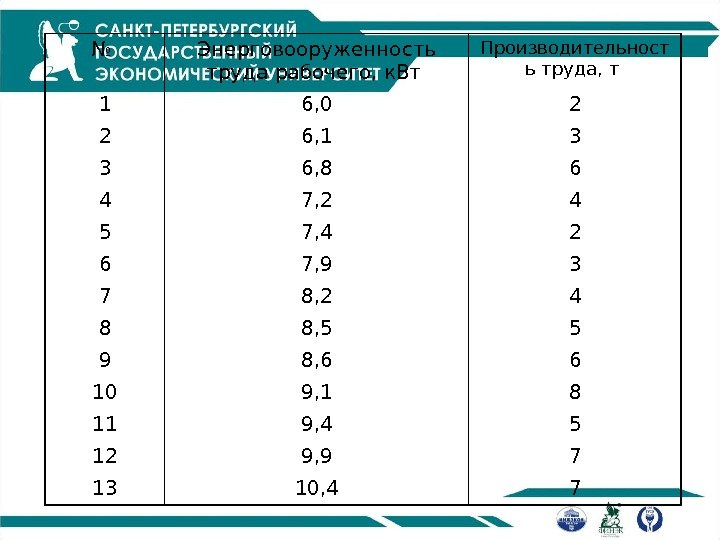
№ Энерговооруженность труда рабочего, к. Вт Производительност ь труда, т 1 6, 0 2 2 6, 1 3 3 6, 8 6 4 7, 2 4 5 7, 4 2 6 7, 9 3 7 8, 2 4 8 8, 5 5 9 8, 6 6 10 9, 1 8 11 9, 4 5 12 9, 9 7 13 10,

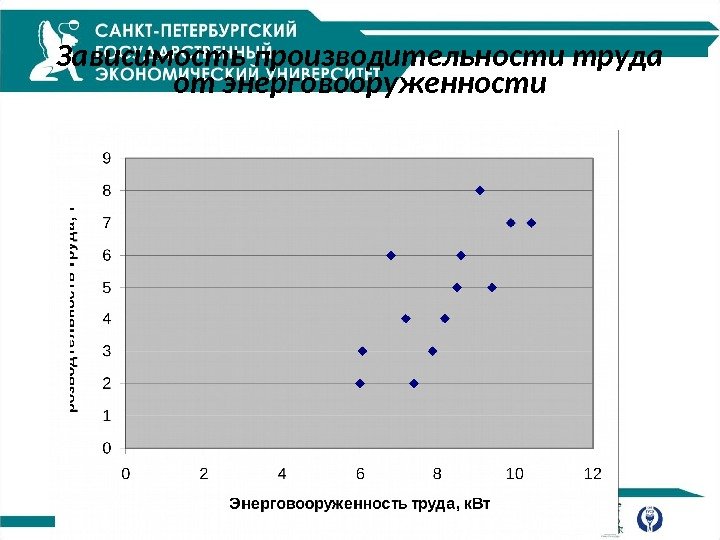
Зависимость производительности труда от энерговооруженности

Показатели силы связи • Характеризуют, на сколько в среднем изменяется результативный признак при изменении факторного признака на одну единицу. 1 1 xx yy b k k

117, 1 75, 675, 9 40, 375, 6 1 1 xx yy b k k

Показатели тесноты связи Оценивают, какую роль играет анализируемый факторный признак в формировании результативного признака

Показатели тесноты связи • Коэффициент детерминации • Эмпирическое корреляционное отношение

Правило сложения дисперсий 222 yyy S

Общая дисперсия результативного признака 2 2 )( yy n yy y

Межгрупповая (факторная) дисперсия j jj y n nyy

Внутригрупповая (остаточная) дисперсия j jy y n n. S S

Коэффициент детерминации 2 2 2 y y

Эмпирическое корреляционное отношение

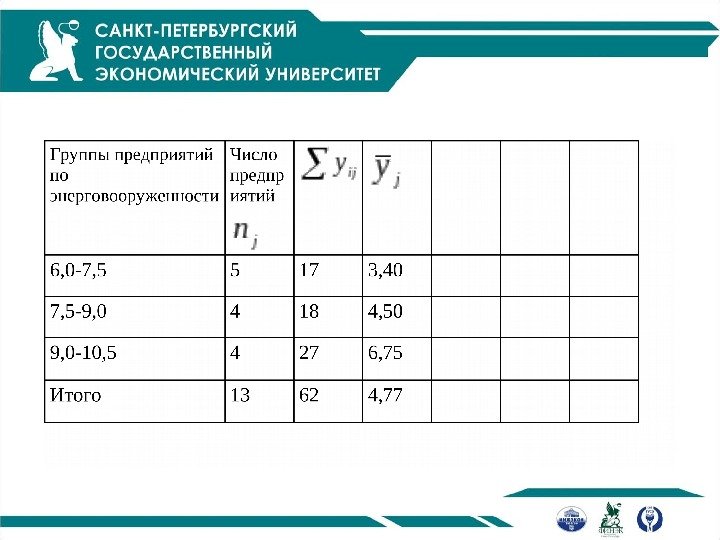
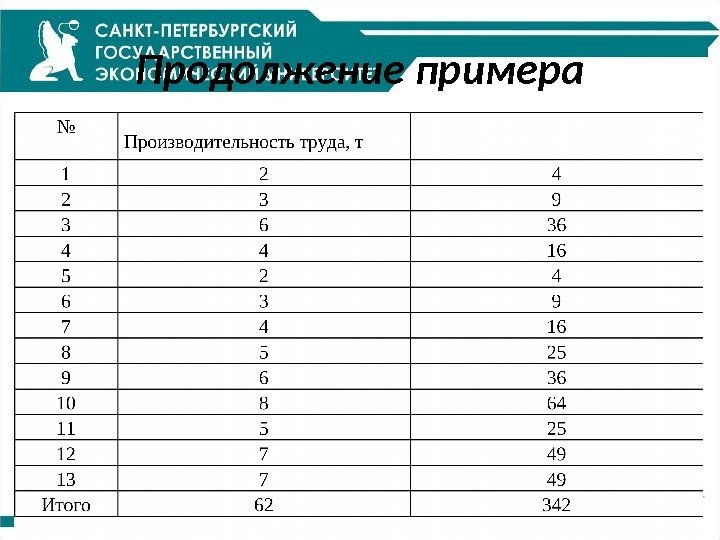
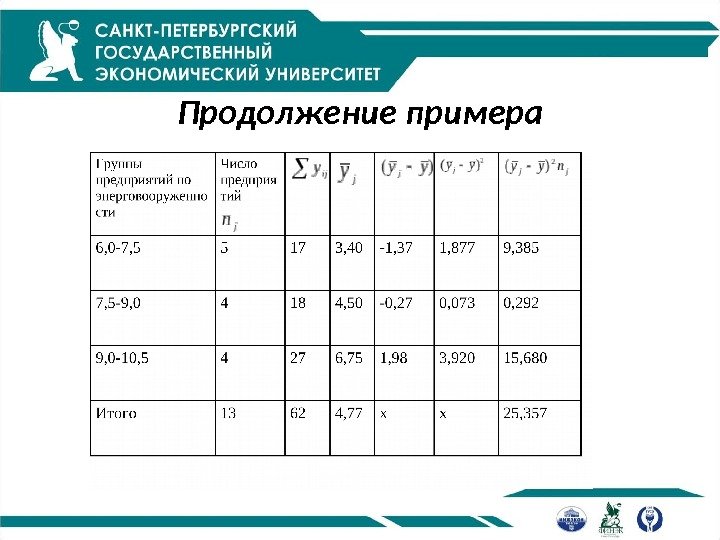
Продолжение примера

Общая дисперсия 56, 375, 2231, 26 )77, 4( 1334222 y

Продолжение примера

Межгрупповая дисперсия 95, 1 13 357, 252 y

Коэффициент детерминации 547, 0 56, 3 95, 1 2 2 2 y y

Эмпирическое корреляционное отношение 740,

Недостатки аналитической группировки • Предполагает только линейную зависимость между признаками • На основе аналитической группировки невозможно прогнозировать явление

ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ • Регрессионный анализ заключается в определении аналитического выражения связи между явлениями, в котором изменение одной величины (зависимой) обусловлено влиянием одной или нескольких независимых величин

Задачи корреляционно-регрессионного анализа • Измерение параметров уравнения, выражающего связь между признаками. Эта задача решается оценкой параметров уравнения регрессии • Измерение тесноты связи между признаками. Данная задача решается с помощью показателей корреляции

Формулы расчета параметров уравнения парной регрессии • — свободный член уравнения регрессии • — коэффициент регрессии 22 xx yxyx b xbya a b

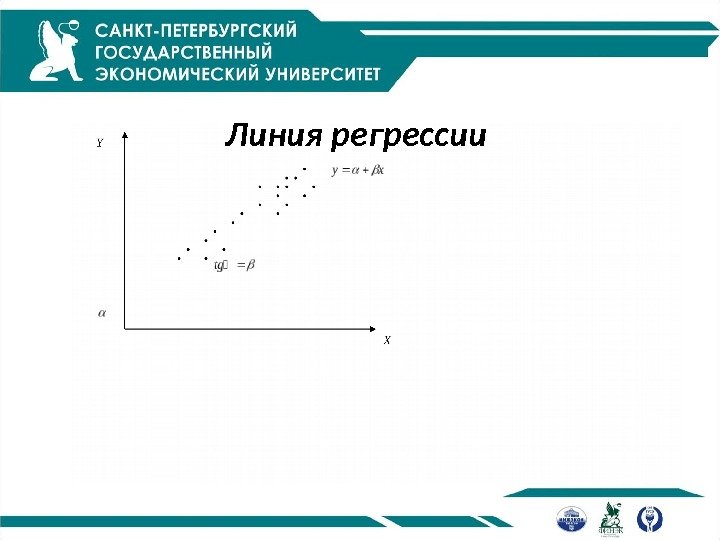
Линия регрессии

Показатели силы связи в моделях парной регрессии • Абсолютные. Показывают, на сколько единиц в среднем меняется результативный признак при изменении факторного признака на одну единицу. В линейном уравнении параметр — абсолютный показатель силы связи • Относительные ( коэффициенты эластичности) Показывают, на сколько процентов в среднем меняется результативный признак при изменении факторного признака на один процент b y x xf. Э

Показатели тесноты связи • Линейный коэффициент корреляции: • Коэффициент детерминации: 2 r xyy x yx xyyx br

• Коэффициент детерминации показывает долю вариации (дисперсии) результативного признака, объясняемую регрессией в общей вариации результата

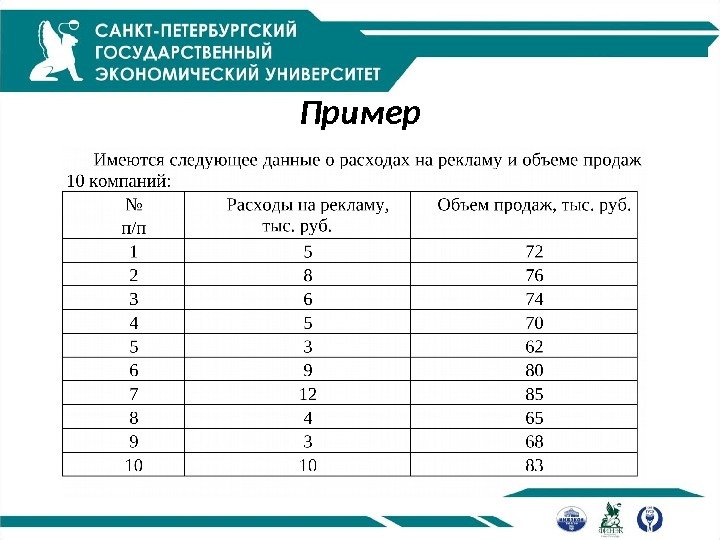
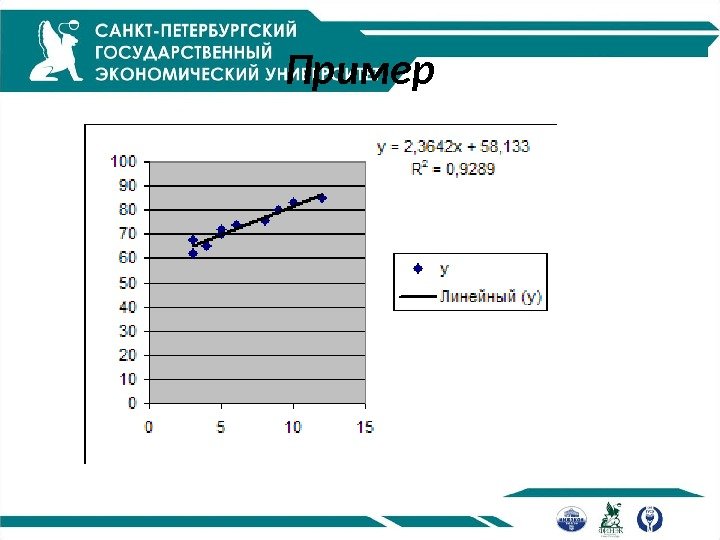
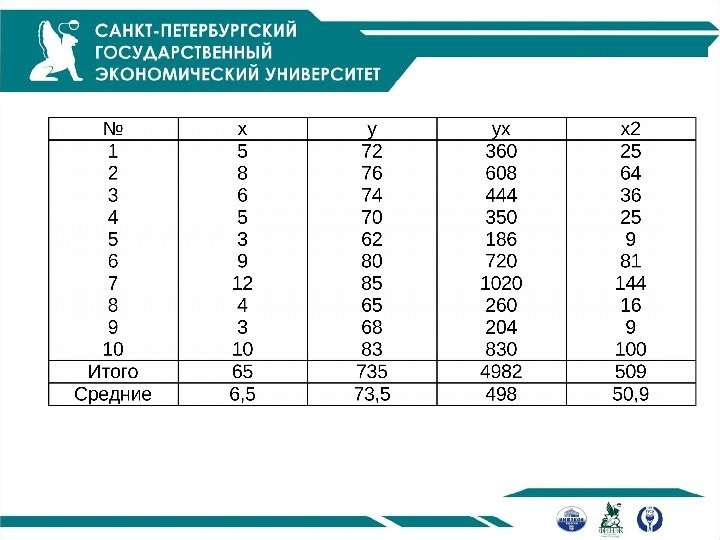
Пример

Пример

215, 705, 525, 733, 5454 222 yyy 941, 265, 85, 69, 50 222 xxx 964, 0 215, 7 941, 2 364, 2 yxbr 929, 02 r