Stability Sem (July 2012).ppt
- Количество слайдов: 35

STABILITY SEMINAR (2 -5 July, 2012 Briese Swallow Co )

Basic Information of A Ship Stability (Основные понятия об остойчивости судна) Stability is a property of a ship disturbed by an external inclining moment of force that changes a ship angular attitude, to return to its original position if this moment removes. Остойчивость – это способность судна, наклоненного на некоторый угол крена (дифферента) внешней силой (моментом), возвращаться в исходное положение после прекращения действия этой силы (момента).
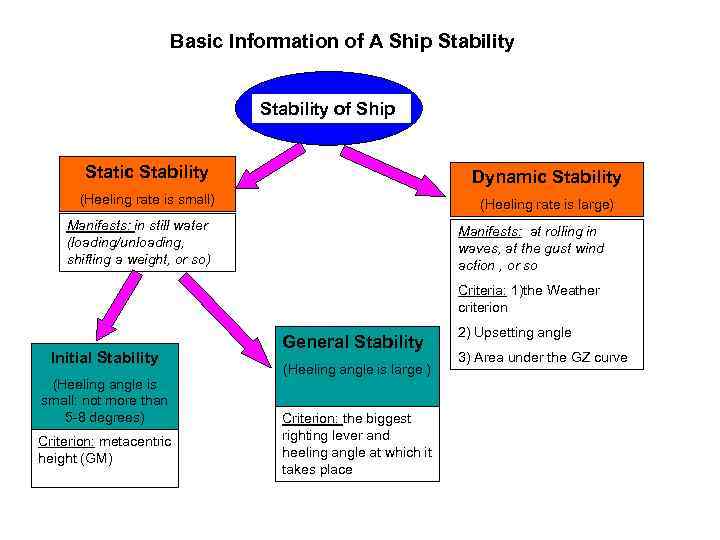
Basic Information of A Ship Stability of Ship Static Stability Dynamic Stability (Heeling rate is small) (Heeling rate is large) Manifests: in still water (loading/unloading, shifting a weight, or so) Manifests: at rolling in waves, at the gust wind action , or so Criteria: 1)the Weather criterion Initial Stability (Heeling angle is small: not more than 5 -8 degrees) Criterion: metacentric height (GM) General Stability (Heeling angle is large ) Criterion: the biggest righting lever and heeling angle at which it takes place 2) Upsetting angle 3) Area under the GZ curve

Fundamentals of mechanics for stability calculation. Понятие силы Сила – это нечто, что воздействует на данное материальное тело, вызывая изменение его скорости или деформацию этого тела. Сила – величина векторная, поэтому как всякий вектор она характеризуется, в общем случае, своим численным значением (длиной вектора или его модулем), направлением в пространстве и точкой приложения. Concept of Force is what that acts at the material body and causes its velocity alteration (acceleration) or deformation. A force is a vector; therefore, as any other vector, it can be defined by such parameters as: the magnitude of the force, the direction in which the force acts, and the point at which this force is applied (point of application). Applied point Line of action Magnitude of force
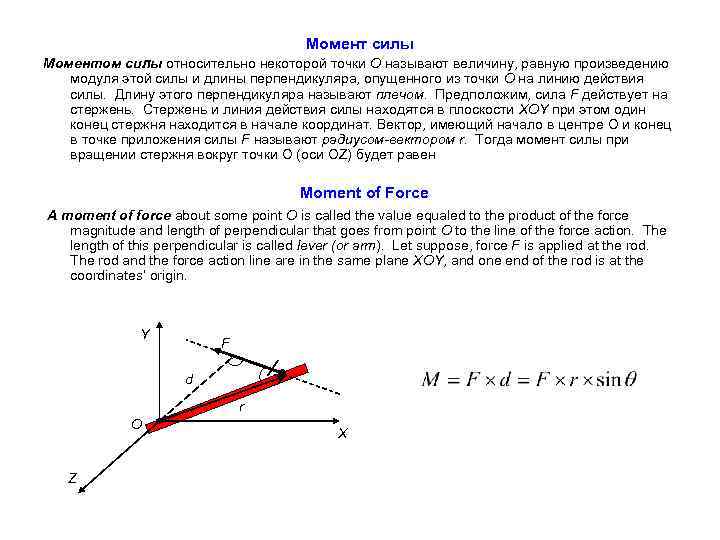
Момент силы Моментом силы относительно некоторой точки О называют величину, равную произведению модуля этой силы и длины перпендикуляра, опущенного из точки O на линию действия силы. Длину этого перпендикуляра называют плечом. Предположим, сила F действует на стержень. Стержень и линия действия силы находятся в плоскости XОY при этом один конец стержня находится в начале координат. Вектор, имеющий начало в центре О и конец в точке приложения силы F называют радиусом-вектором r. Тогда момент силы при вращении стержня вокруг точки О (оси OZ) будет равен Moment of Force A moment of force about some point O is called the value equaled to the product of the force magnitude and length of perpendicular that goes from point O to the line of the force action. The length of this perpendicular is called lever (or arm). Let suppose, force F is applied at the rod. The rod and the force action line are in the same plane XOY, and one end of the rod is at the coordinates’ origin. Y F d r O Z X

Момент пары сил Парой сил называют два параллельных вектора, имеющих равные модули и действующих в противоположных направлениях. Примерами пары сил могут служить сила тяжести и выталкивающая сила, действующие на судно при его наклонении, сила постоянного ветра, приложенная в надводной части судна, и сила сопротивления воды, возникшая в подводной части, как реакция на боковое смещение (дрейф) судна под действием этого ветра, и. т. д. Если в кусок пенопласта, спокойно плавающего в воде, забить два гвоздика, привязать к ним нити и потянуть за них (как показано на рис. 1. 6), то возникнет пара сил, которая начнет вращать кусок пенопласта. При этом интенсивность вращения (вращательный эффект) будет тем больше, чем больше приложенные силы натяжения нитей и больше расстояние между линиями действия этих сил. Moment of Couple A couple is called a pair of collinear forces of equal magnitude acting in parallel but opposite directions. M F 1 B A A l F 2
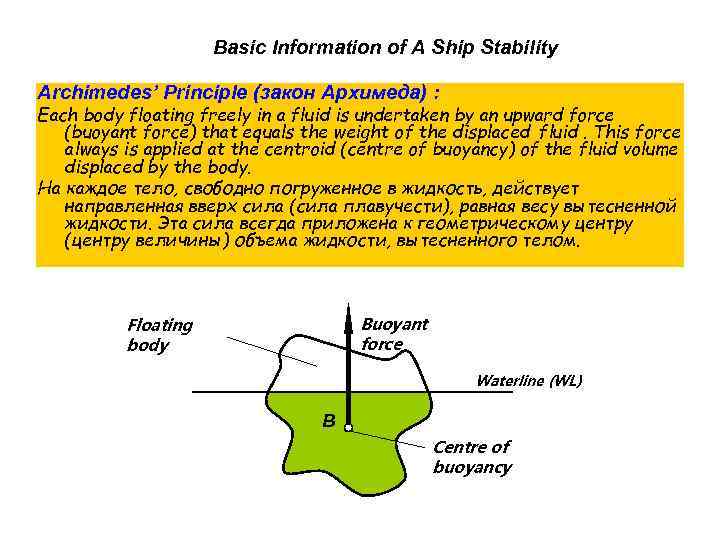
Basic Information of A Ship Stability Archimedes’ Principle (закон Архимеда) : Each body floating freely in a fluid is undertaken by an upward force (buoyant force) that equals the weight of the displaced fluid. This force always is applied at the centroid (centre of buoyancy) of the fluid volume displaced by the body. На каждое тело, свободно погруженное в жидкость, действует направленная вверх сила (сила плавучести), равная весу вытесненной жидкости. Эта сила всегда приложена к геометрическому центру (центру величины) объема жидкости, вытесненного телом. Buoyant force Floating body Waterline (WL) B Centre of buoyancy
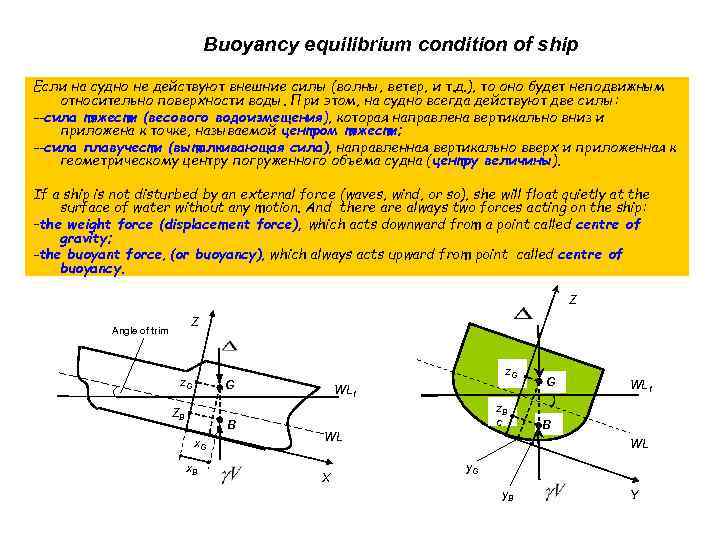
Buoyancy equilibrium condition of ship Если на судно не действуют внешние силы (волны, ветер, и т. д. ), то оно будет неподвижным относительно поверхности воды. При этом, на судно всегда действуют две силы: --сила тяжести (весового водоизмещения), которая направлена вертикально вниз и приложена к точке, называемой центром тяжести; --сила плавучести (выталкивающая сила), направленная вертикально вверх и приложенная к геометрическому центру погруженного объема судна (центру величины). If a ship is not disturbed by an external force (waves, wind, or so), she will float quietly at the surface of water without any motion. And there always two forces acting on the ship: –the weight force (displacement force), which acts downward from a point called centre of gravity; -the buoyant force, (or buoyancy), which always acts upward from point called centre of buoyancy. Z Z Angle of trim z. G G WL 1 z. B ZB B x. G x. B B C WL X WL y. G y. B Y
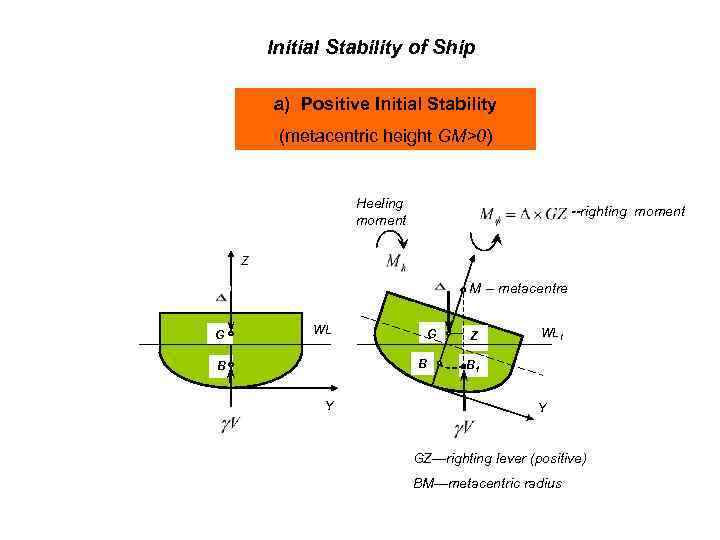
Initial Stability of Ship a) Positive Initial Stability (metacentric height GM>0) Heeling moment --righting moment Z M -- metacentre G WL GZ B B Y Z WL 1 B 1 Y GZ—righting lever (positive) BM—metacentric radius
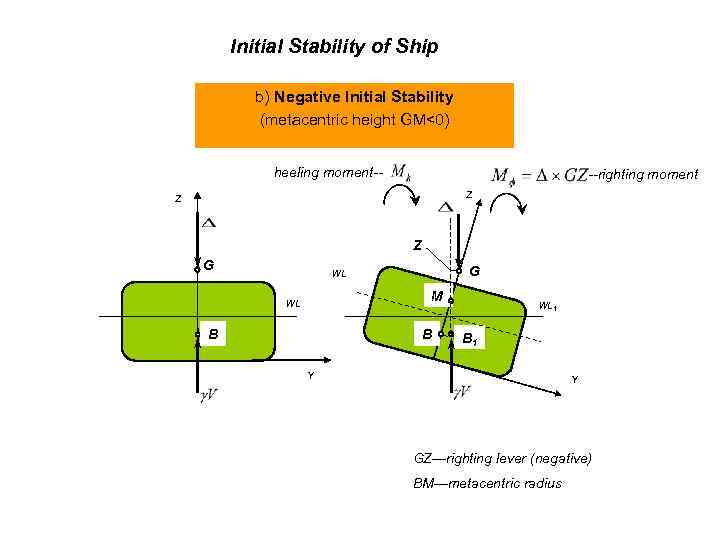
Initial Stability of Ship b) Negative Initial Stability (metacentric height GM<0) heeling moment-- --righting moment Z Z Z G G WL M WL B B WL 1 B 1 Y Y GZ—righting lever (negative) BM—metacentric radius
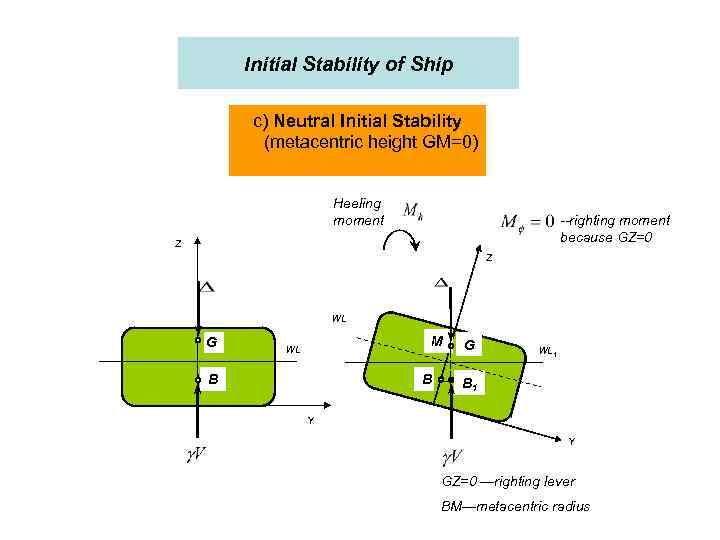
Initial Stability of Ship c) Neutral Initial Stability (metacentric height GM=0) Heeling moment --righting moment because GZ=0 Z Z WL G M WL B B G WL 1 B 1 Y Y GZ=0 —righting lever BM—metacentric radius
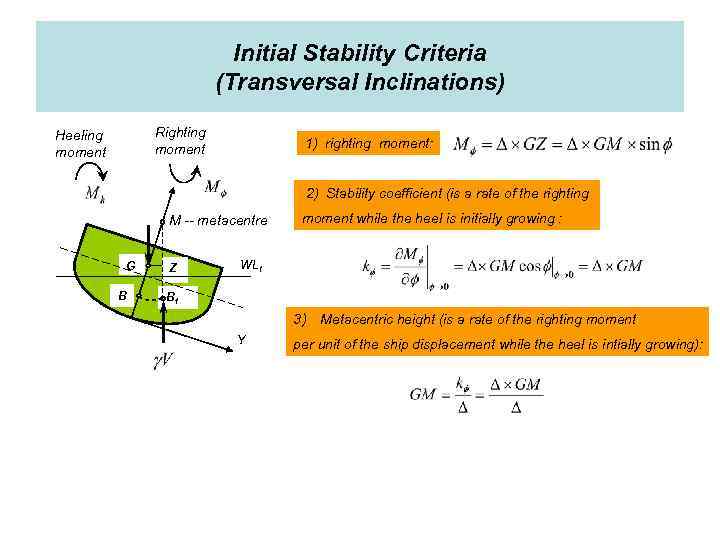
Initial Stability Criteria (Transversal Inclinations) Righting moment Heeling moment 1) righting moment: 2) Stability coefficient (is a rate of the righting M -- metacentre GZ B Z moment while the heel is initially growing : WL 1 B 1 3) Metacentric height (is a rate of the righting moment Y per unit of the ship displacement while the heel is intially growing):
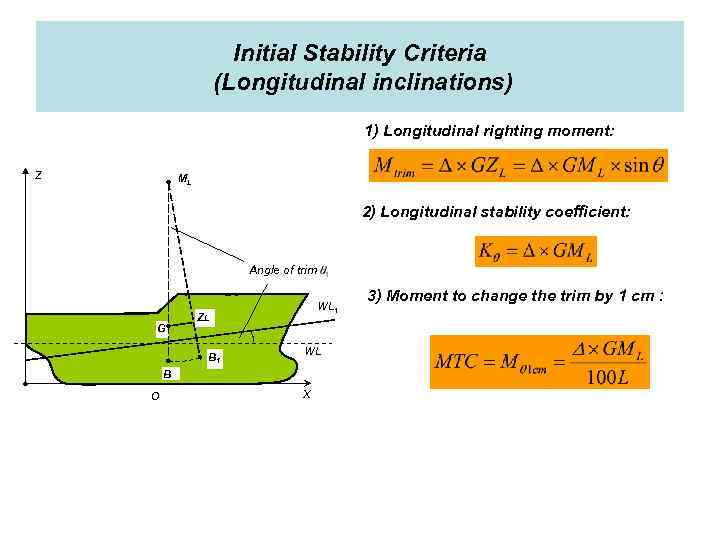
Initial Stability Criteria (Longitudinal inclinations) 1) Longitudinal righting moment: Z ML 2) Longitudinal stability coefficient: Angle of trim G WL 1 ZL B 1 WL B O X 3) Moment to change the trim by 1 cm :
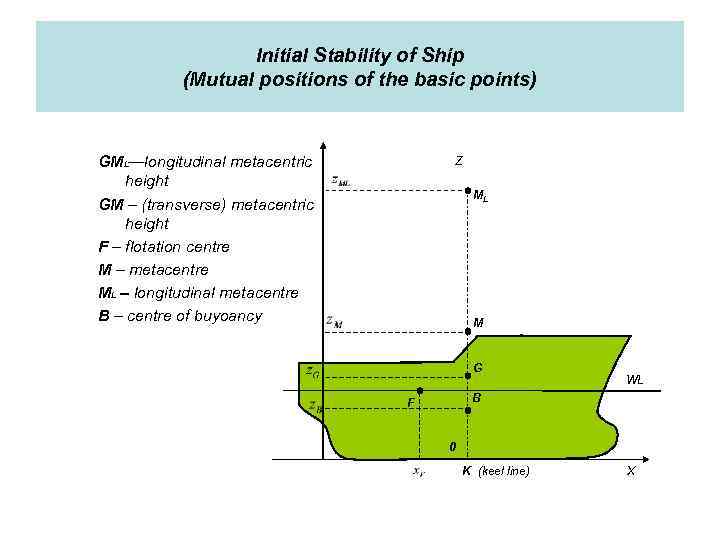
Initial Stability of Ship (Mutual positions of the basic points) GML—longitudinal metacentric height GM – (transverse) metacentric height F – flotation centre M – metacentre ML – longitudinal metacentre B – centre of buyoancy Z ML M G WL B F 0 K (keel line) X
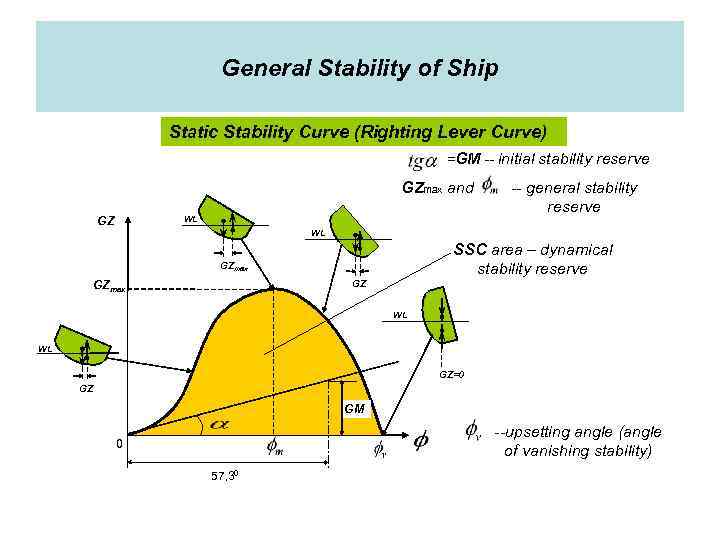
General Stability of Ship Static Stability Curve (Righting Lever Curve) =GM -- initial stability reserve GZmax and WL GZ -- general stability reserve WL SSC area – dynamical stability reserve GZmax GZ GZmax WL WL GZ=0 GZ GM --upsetting angle (angle of vanishing stability) 0 57, 30
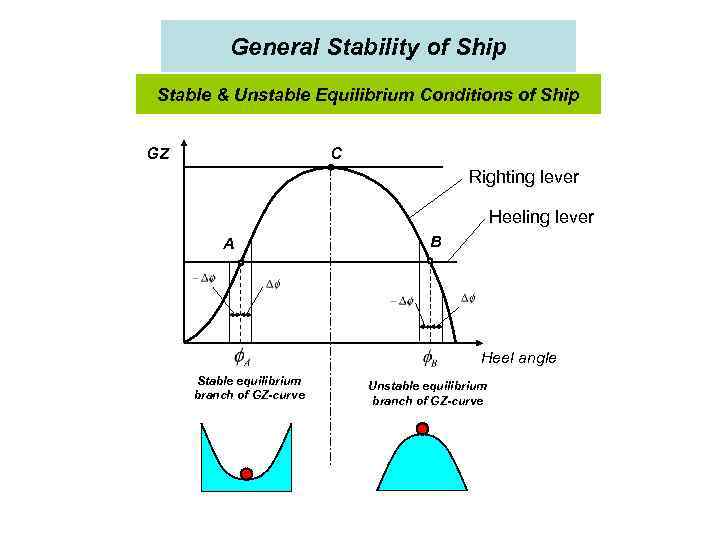
General Stability of Ship Stable & Unstable Equilibrium Conditions of Ship GZ C Righting lever Heeling lever A B Heel angle Stable equilibrium branch of GZ-curve Unstable equilibrium branch of GZ-curve
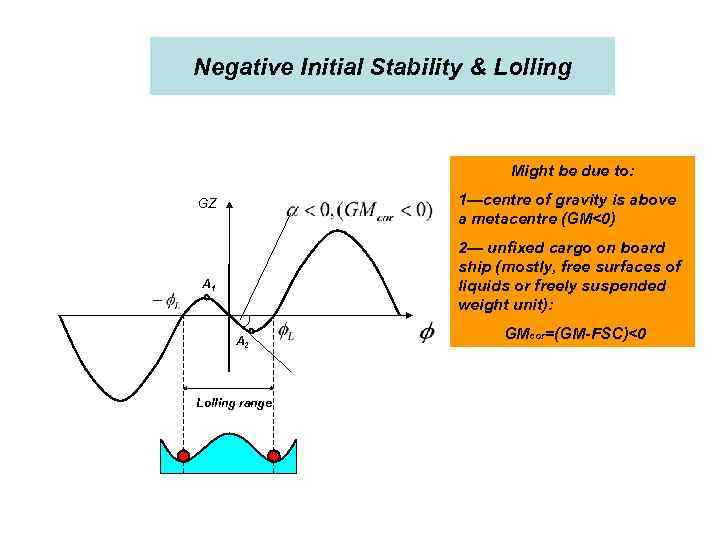
Negative Initial Stability & Lolling Might be due to: 1—centre of gravity is above a metacentre (GM<0) GZ 2— unfixed cargo on board ship (mostly, free surfaces of liquids or freely suspended weight unit): A 1 A 2 Lolling range GMcor=(GM-FSC)<0
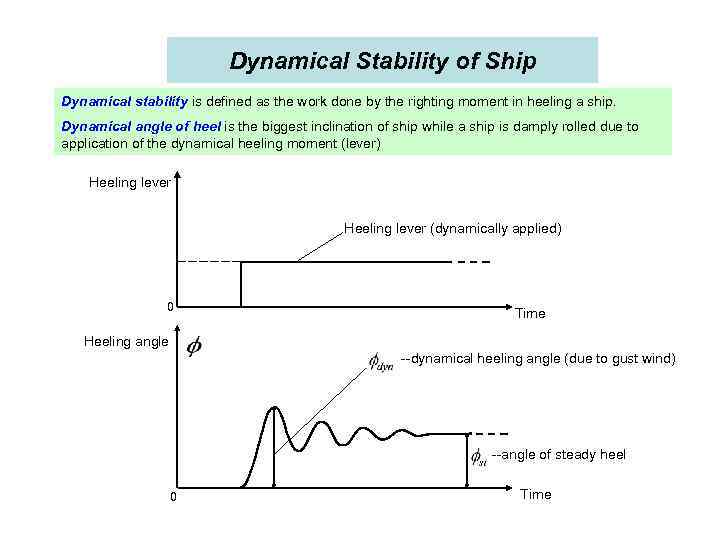
Dynamical Stability of Ship Dynamical stability is defined as the work done by the righting moment in heeling a ship. Dynamical angle of heel is the biggest inclination of ship while a ship is damply rolled due to application of the dynamical heeling moment (lever) Heeling lever (dynamically applied) 0 Time Heeling angle --dynamical heeling angle (due to gust wind) --angle of steady heel 0 Time
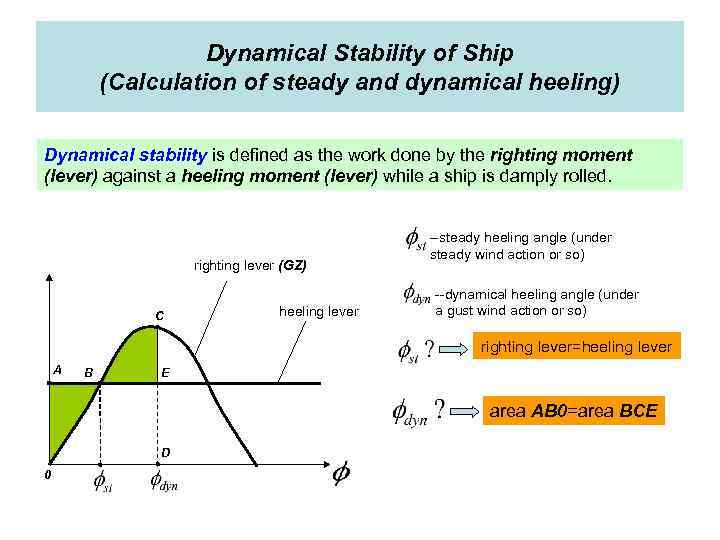
Dynamical Stability of Ship (Calculation of steady and dynamical heeling) Dynamical stability is defined as the work done by the righting moment (lever) against a heeling moment (lever) while a ship is damply rolled. righting lever (GZ) C heeling lever --steady heeling angle (under steady wind action or so) --dynamical heeling angle (under a gust wind action or so) righting lever=heeling lever A B E area AB 0=area BCE D 0
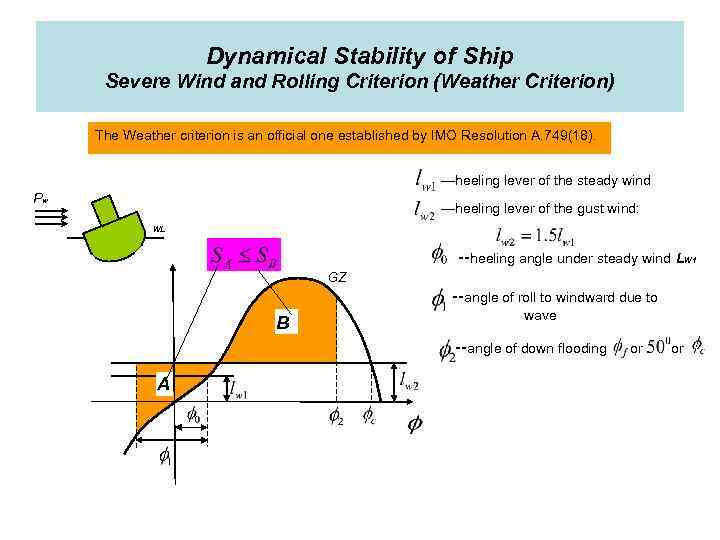
Dynamical Stability of Ship Severe Wind and Rolling Criterion (Weather Criterion) The Weather criterion is an official one established by IMO Resolution A. 749(18). —heeling lever of the steady wind Pw —heeling lever of the gust wind: WL --heeling angle under steady wind LW 1 GZ --angle of roll to windward due to B wave --angle of down flooding A or or
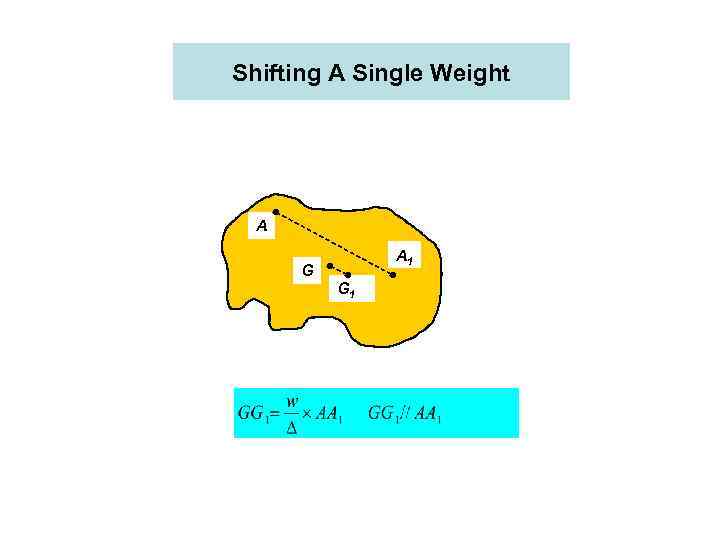
Shifting A Single Weight A A 1 G G 1
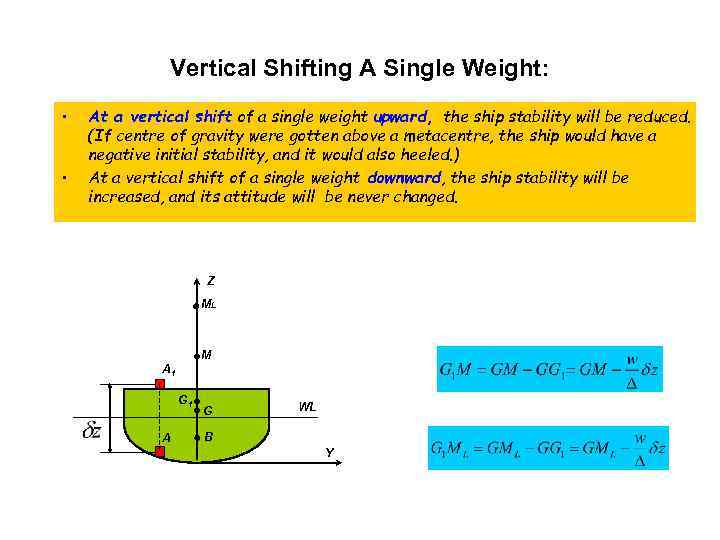
Vertical Shifting A Single Weight: • • At a vertical shift of a single weight upward, the ship stability will be reduced. (If centre of gravity were gotten above a metacentre, the ship would have a negative initial stability, and it would also heeled. ) At a vertical shift of a single weight downward, the ship stability will be increased, and its attitude will be never changed. Z ML M A 1 G 1 A G WL B Y
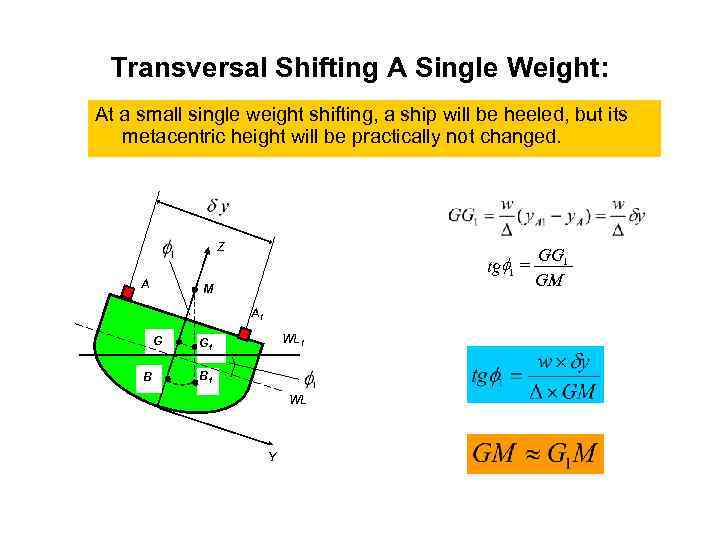
Transversal Shifting A Single Weight: At a small single weight shifting, a ship will be heeled, but its metacentric height will be practically not changed. Z A tgf 1 = M A 1 G B WL 1 G 1 B 1 WL Y GG 1 GM
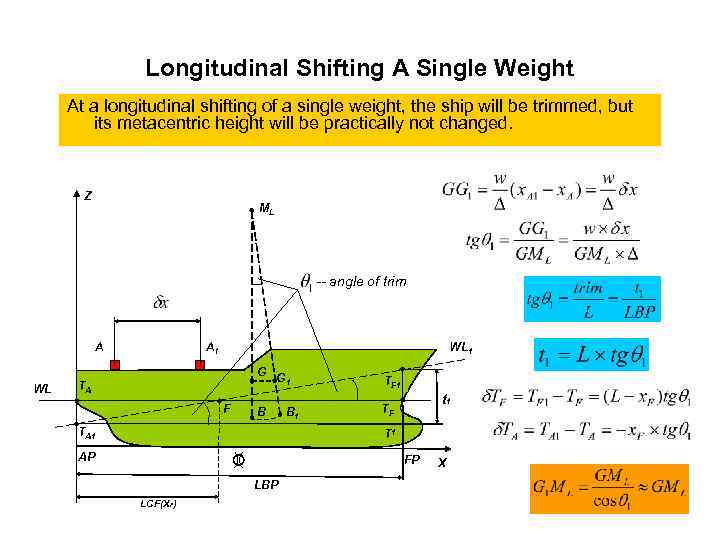
Longitudinal Shifting A Single Weight At a longitudinal shifting of a single weight, the ship will be trimmed, but its metacentric height will be practically not changed. Z ML -- angle of trim A WL WL 1 A 1 G G 1 TA F TF 1 B TF TA 1 B 1 t 1 T 1 AP FP LBP LCF(XF) X
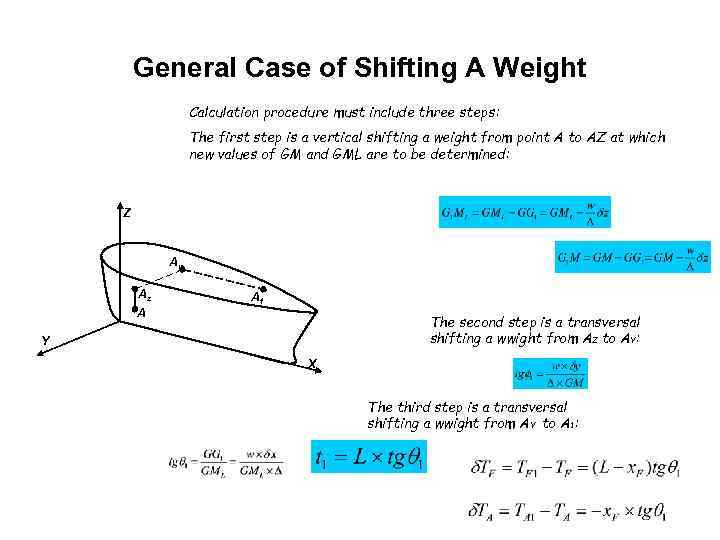
General Case of Shifting A Weight Сalculation procedure must include three steps: The first step is a vertical shifting a weight from point A to AZ at which new values of GM and GML are to be determined: Z Ay Az A 1 A The second step is a transversal shifting a wwight from AZ to AY: Y X The third step is a transversal shifting a wwight from AY to A 1:

A Freely Suspended Weight At the very moment of suspension of a single weight (by the ship crane), the effect on the ship’s stability is looked like a situation when this weight is immediately lifted up at the point of suspension (point S). Consequently, a subsequent real lifting or lowing of the suspended weight does not affected on the ship stability anymore. Heeling moment due to suspension: Z S M Berth Metacentric height (corrected due to suspended weight): WL 1 G A A 0 WL 0 Y
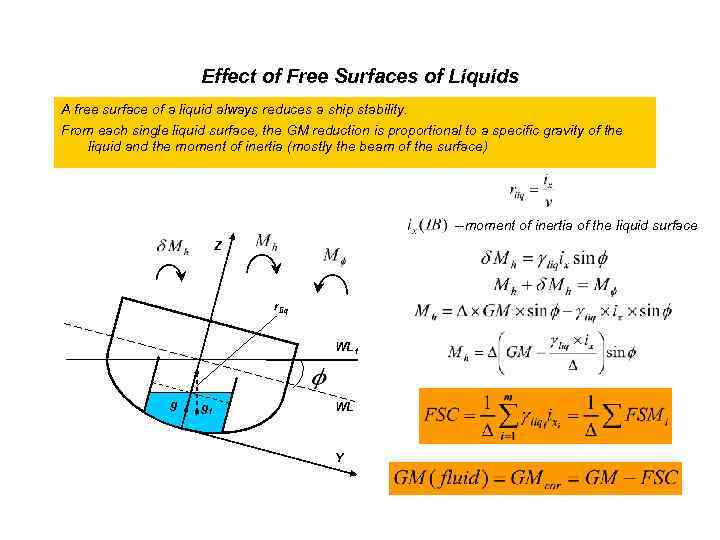
Effect of Free Surfaces of Liquids A free surface of a liquid always reduces a ship stability. From each single liquid surface, the GM reduction is proportional to a specific gravity of the liquid and the moment of inertia (mostly the beam of the surface) --moment of inertia of the liquid surface Z rliq WL 1 g g 1 WL Y
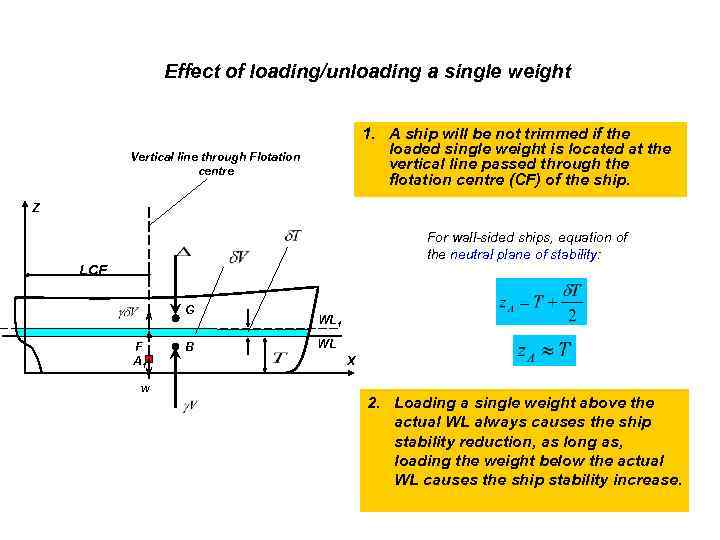
Effect of loading/unloading a single weight 1. A ship will be not trimmed if the loaded single weight is located at the vertical line passed through the flotation centre (CF) of the ship. Vertical line through Flotation centre Z For wall-sided ships, equation of the neutral plane of stability: LCF G F A 1 w B WL 1 WL X 2. Loading a single weight above the actual WL always causes the ship stability reduction, as long as, loading the weight below the actual WL causes the ship stability increase.
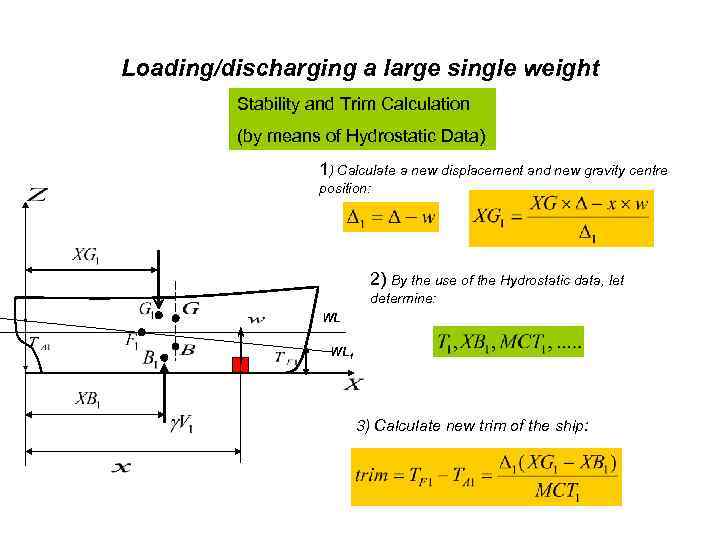
Loading/discharging a large single weight Stability and Trim Calculation (by means of Hydrostatic Data) 1) Calculate a new displacement and new gravity centre position: 2) By the use of the Hydrostatic data, let determine: WL WL 1 3) Calculate new trim of the ship:
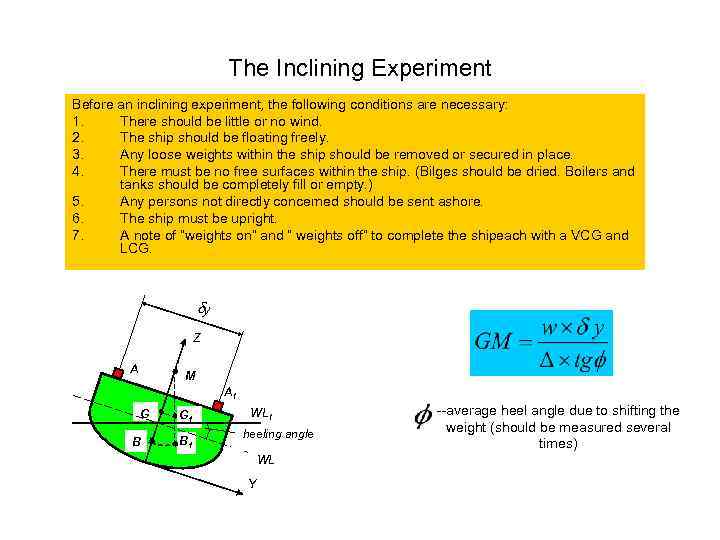
The Inclining Experiment Before an inclining experiment, the following conditions are necessary: 1. There should be little or no wind. 2. The ship should be floating freely. 3. Any loose weights within the ship should be removed or secured in place. 4. There must be no free surfaces within the ship. (Bilges should be dried. Boilers and tanks should be completely fill or empty. ) 5. Any persons not directly concerned should be sent ashore. 6. The ship must be upright. 7. A note of “weights on” and “ weights off” to complete the shipeach with a VCG and LCG. dy Z A M A 1 G B G 1 B 1 WL 1 heeling angle WL Y --average heel angle due to shifting the weight (should be measured several times)
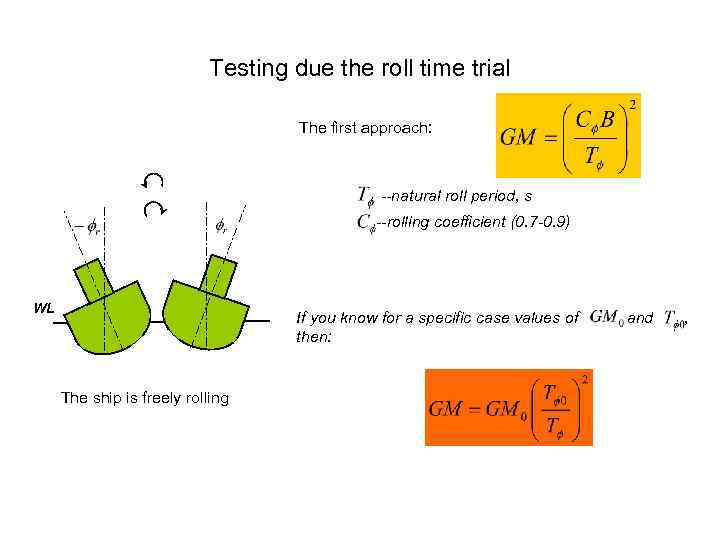
Testing due the roll time trial The first approach: --natural roll period, s --rolling coefficient (0. 7 -0. 9) WL If you know for a specific case values of then: The ship is freely rolling and ,
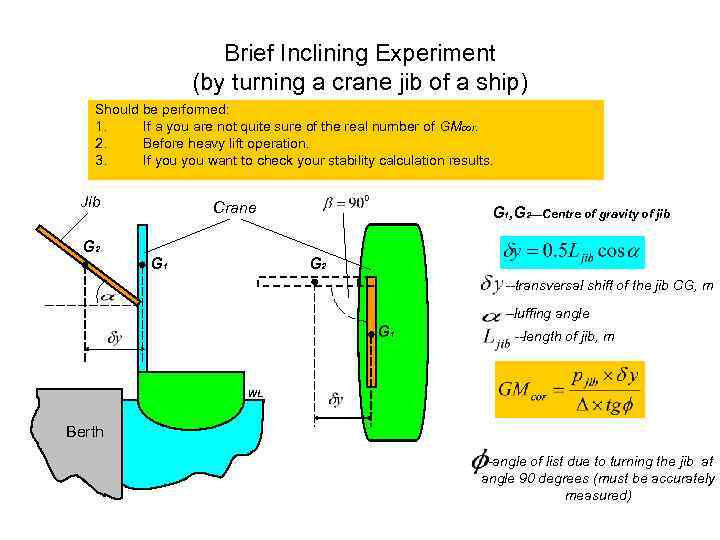
Brief Inclining Experiment (by turning a crane jib of a ship) Should be performed: 1. If а you are not quite sure of the real number of GMcor. 2. Before heavy lift operation. 3. If you want to check your stability calculation results. Jib G 2 Crane G 1, G 2—Centre of gravity of jib G 2 --transversal shift of the jib CG, m --luffing angle G 1 --length of jib, m WL Berth --angle of list due to turning the jib at angle 90 degrees (must be accurately measured)
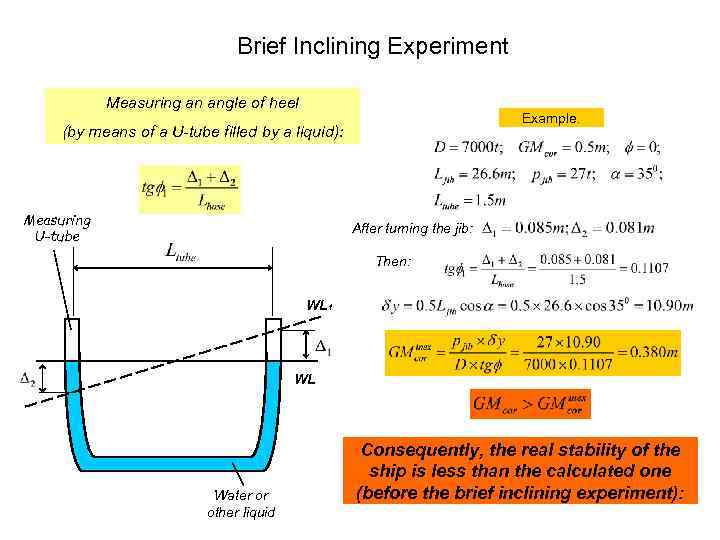
Brief Inclining Experiment Measuring an angle of heel Example. (by means of a U-tube filled by a liquid): Measuring U-tube After turning the jib: Then: WL 1 WL Water or other liquid Consequently, the real stability of the ship is less than the calculated one (before the brief inclining experiment):
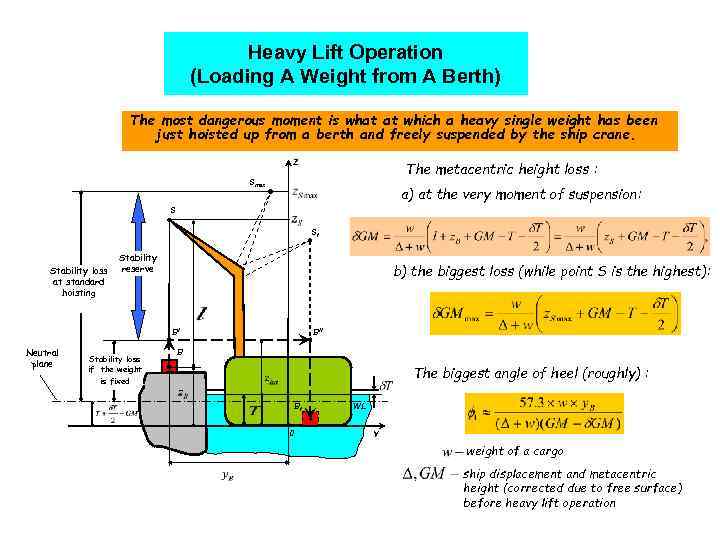
Heavy Lift Operation (Loading A Weight from A Berth) The most dangerous moment is what at which a heavy single weight has been just hoisted up from a berth and freely suspended by the ship crane. Z The metacentric height loss : Smax a) at the very moment of suspension: S S 1 Stability loss at standard hoisting Stability reserve b) the biggest loss (while point S is the highest): BI Neutral plane Stability loss if the weight is fixed BII B The biggest angle of heel (roughly) : B 1 0 WL Y weight of a cargo ship displacement and metacentric height (corrected due to free surface) before heavy lift operation
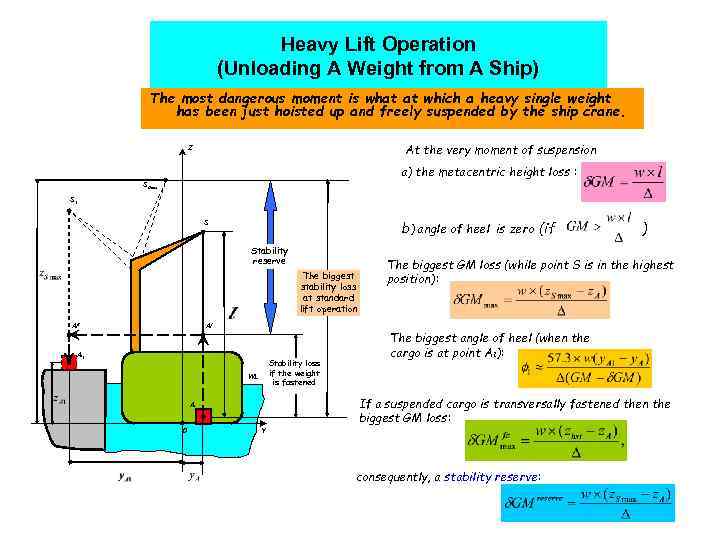
Heavy Lift Operation (Unloading A Weight from A Ship) The most dangerous moment is what at which a heavy single weight has been just hoisted up and freely suspended by the ship crane. At the very moment of suspension Z a) the metacentric height loss : Smax S 1 b) angle of heel is zero (if S Stability reserve The biggest stability loss at standard lift operation AII AI A 1 Stability loss if the weight is fastened WL The biggest GM loss (while point S is in the highest position): The biggest angle of heel (when the cargo is at point A 1): If a suspended cargo is transversally fastened then the biggest GM loss: A 0 ) Y consequently, a stability reserve:
Stability Sem (July 2012).ppt