Средние величины в статистике Средняя арифметическая применяется

Средние величины в статистике

Средняя арифметическая применяется, когда разрыв между минимальным и максимальным значениями признака достаточно невелик или же характер изменения данных при переходе от одной варианты к другой приближенно можно свести к правилу арифметической прогрессии. Средняя арифметическая вычисляется либо как простая, либо как взвешенная величина. Пример. Имеются данные о величине рентабельности по десяти малым предприятиям (%): 10, 12, 15, 15, 17, 20. Средняя рентабельность составит:

Величина соответствует средней арифметической простой: , где – варианты (отдельные значения признака), п – объем совокупности.

Сгруппируем данные: Рентабельность, % Количество предприятий 10 12 15 17 20 1 2 3 2 2 Итого 10 Формула средней арифметической взвешенной: , где fi – частота.

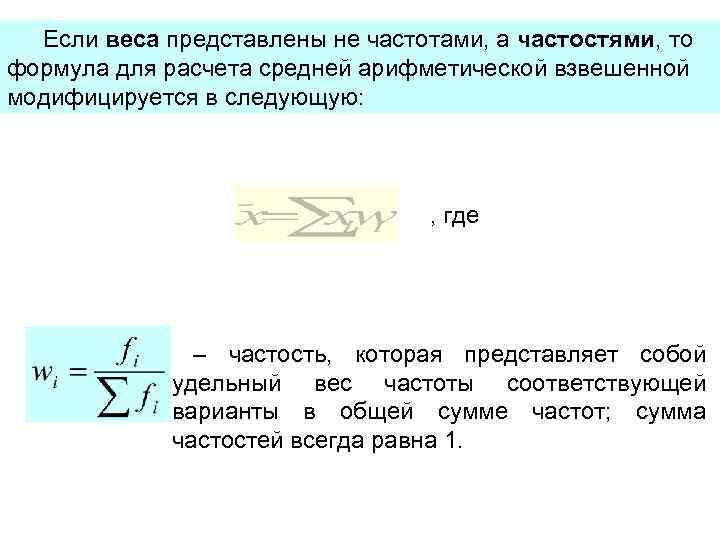Если веса представлены не частотами, а частостями, то формула для расчета средней арифметической взвешенной модифицируется в следующую: , где – частость, которая представляет собой удельный вес частоты соответствующей варианты в общей сумме частот; сумма частостей всегда равна 1.

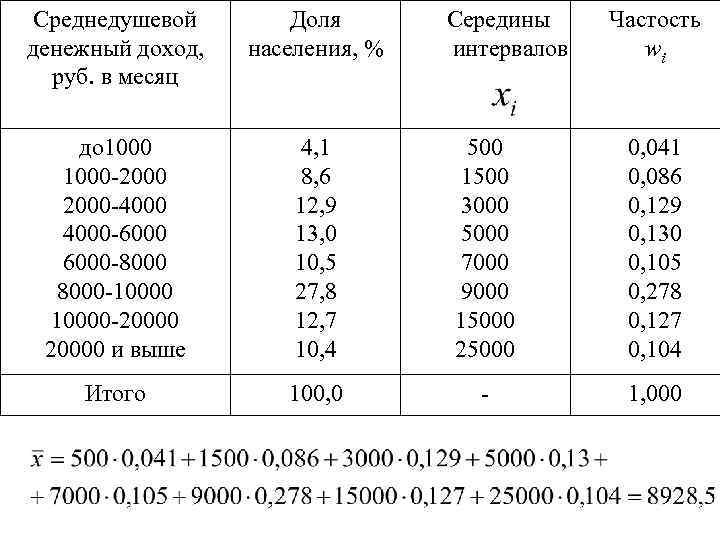Среднедушевой денежный доход, руб. в месяц Доля населения, % до 1000 -2000 -4000 -6000 -8000 -10000 -20000 и выше 4, 1 8, 6 12, 9 13, 0 10, 5 27, 8 12, 7 10, 4 500 1500 3000 5000 7000 9000 15000 25000 0, 041 0, 086 0, 129 0, 130 0, 105 0, 278 0, 127 0, 104 Итого 100, 0 - 1, 000 Середины интервалов Частость wi

Средняя гармоническая Средняя взвешенная гармоническая величина применяется в тех случаях, когда не известны значения частот у вариант ряда, но имеются для каждого xi произведения этих вариант на соответствующие им частоты, т. е. Величиной Fi может быть товарооборот по видам товаров при расчете средней их цены; фонды заработной платы у отдельных категорий работников при расчете средней заработной платы; стоимостные объемы сделок при покупке валют, ценных бумаг, биржевых продажах и т. д.

Формула средней гармонической взвешенной: где xi – значения вариант; Fi – значение произведения варианты на соответствующую ей частоту.

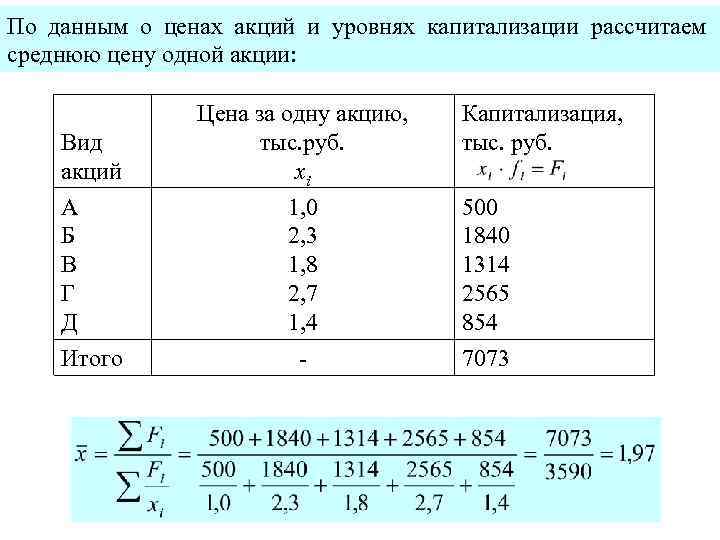По данным о ценах акций и уровнях капитализации рассчитаем среднюю цену одной акции: Вид акций А Б В Г Д Итого Цена за одну акцию, тыс. руб. xi 1, 0 2, 3 1, 8 2, 7 1, 4 - Капитализация, тыс. руб. 500 1840 1314 2565 854 7073

Если произведения вариант на соответствующие им частоты равны между собой (при этом мы можем их не знать, но известно об их равенствах), т. е. , то применяется средняя гармоническая простая , где п – объем совокупности. Пример Предприятием были выделены одинаковые денежные суммы на приобретение акций двух видов, при этом цена акции вида А составляла 1000 руб. , В – 1800 руб. Рассчитаем среднюю цену приобретения акций:

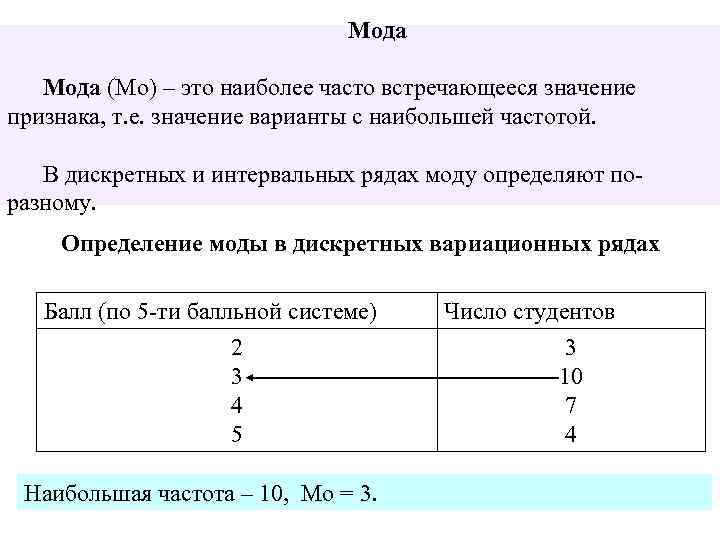Мода (Мо) – это наиболее часто встречающееся значение признака, т. е. значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду определяют поразному. Определение моды в дискретных вариационных рядах Балл (по 5 -ти балльной системе) 2 3 4 5 Наибольшая частота – 10, Мо = 3. Число студентов 3 10 7 4

Определение моды в интервальных вариационных рядах с равными интервалами. Находят модальный интервал (интервал с наибольшей частотой), затем ведут расчет по формуле: , где – нижняя граница модального интервала, d – величина интервала, – частота модального интервала, – частота интервала, предшествующего модальному, – частота интервала, следующего за модальным.

Пример Имеются следующие данные по группе банков: Сумма выданных кредитов, млн. ден. ед. До 40 40– 60 60– 80 80– 100– 120– 140 и выше Количество банков 8 15 21 12 9 7 4 Определим модальный размер выданных кредитов:

Структурные средние Медианой (Ме) является значение варианты, находящейся в центре упорядоченной по возрастанию значений признака совокупности. Медиана делит вариационный ряд на две равные части. При этом 50 % единиц совокупности имеют значение меньше медианного, 50 % – больше медианного. Квартили делят вариационный ряд на четыре равные части: первый квартиль (Q 1) показывает значение признака, которого не превышают значения 25 % единиц совокупности, второй квартиль (Q 2) – 50 % (он совпадает с медианой), третий (Q 3) – 75 % • 25 % • 50 % • 75 % • Q 1 Me, Q 2 Q 3 •

Децили (D)делят упорядоченную по возрастанию значений признака совокупность на десять равных частей: первый дециль показывает значение признака, которого не превышают значения 10 % единиц совокупности, второй – 20 %, третий – 30 % и т. д. При этом пятый дециль совпадает с медианой и вторым квартилем. • 10 % 20 % 30 % 40 % 50 % 60 % 70 % 80 % 90 % • • • D 1 D 2 D 3 D 4 D 5 Me, Q 2 D 6 D 7 D 8 D 9 •

Определение структурных средних в дискретных вариационных рядах Для определения медианы сначала находят ее порядковый номер по формуле: , где п – объем совокупности, Номера квартилей: Номера децилей: и т. д.

Медианой (квартилем, децилем) является значение признака, у которого накопленная частота начинает впервые превышать номер медианы (квартиля, дециля).

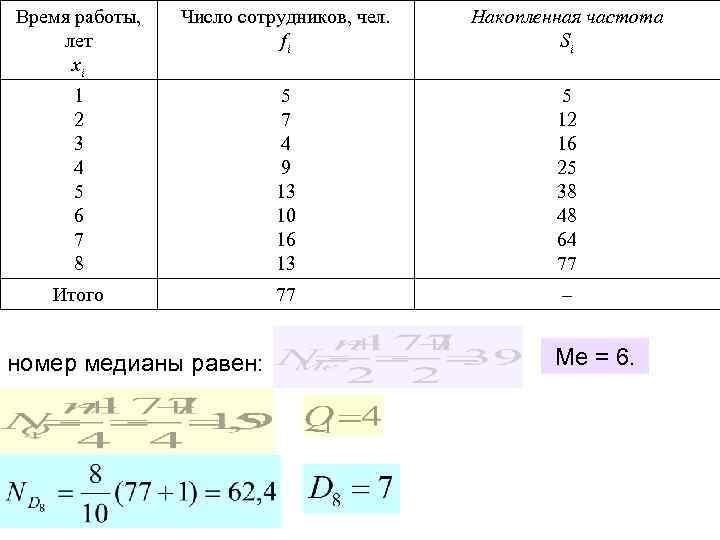Время работы, лет хi Число сотрудников, чел. fi Накопленная частота Si 1 2 3 4 5 6 7 8 5 7 4 9 13 10 16 13 5 12 16 25 38 48 64 77 Итого 77 – номер медианы равен: Ме = 6.

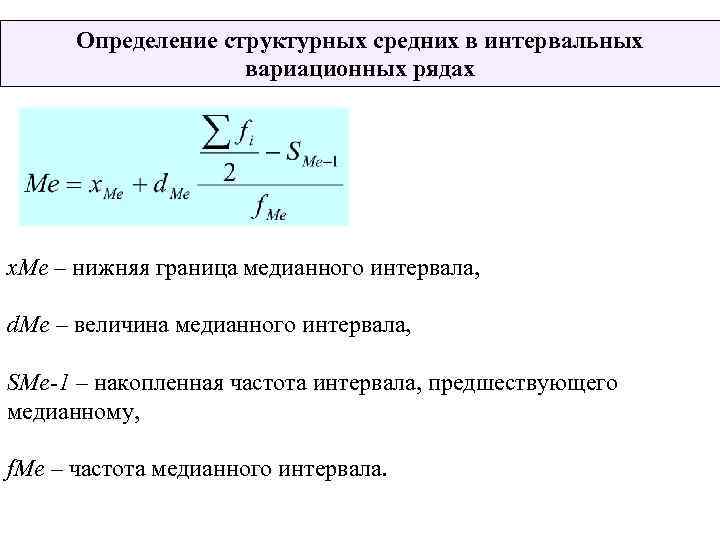Определение структурных средних в интервальных вариационных рядах х. Ме – нижняя граница медианного интервала, d. Me – величина медианного интервала, SMe-1 – накопленная частота интервала, предшествующего медианному, f. Me – частота медианного интервала.

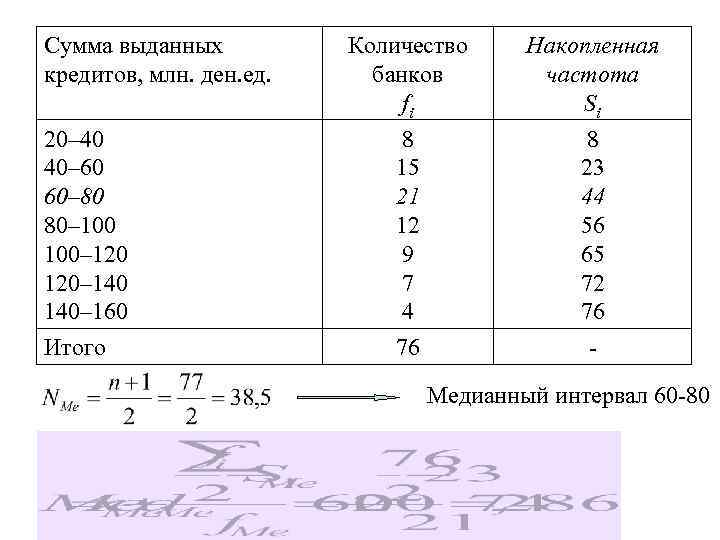Сумма выданных кредитов, млн. ден. ед. 20– 40 40– 60 60– 80 80– 100– 120– 140– 160 Итого Количество банков fi 8 15 21 12 9 7 4 76 Накопленная частота Si 8 23 44 56 65 72 76 - Медианный интервал 60 -80

Квартили. первый (нижний) квартиль: третий (верхний) квартиль:

Номер первого квартиля: первый квартиль равен Номер третьего квартиля: Значение третьего квартиля:

Формулы для расчета децилей в интервальных вариационных рядах и т. д.