Статистика.3..pptx
- Количество слайдов: 9

Средние величины Средняя величина – это обобщающая характеристика изменяющегося количественного признака однородной совокупности. Она выражает наиболее общие свойства явлений или процессов, типичные для всей совокупности, и не учитывает влияние индивидуальных особенностей. (!) Средняя величина позволяет охарактеризовать всю совокупность одним числом. Как правило, расчет средних величин происходит после группировки исходных данных.

Пример В университете Оксфорда учатся люди разных возрастов (от вундеркиндов до пожилых людей). С помощью средней величины мы можем определить сколько лет среднестатистическому студенту Оксфорда – 22 года. Однородная совокупность – студенты Оксфорда, Изменяющийся количественный признак – возраст, Средняя величина дает обобщающую характеристику возраста студентов Оксфорда в целом.
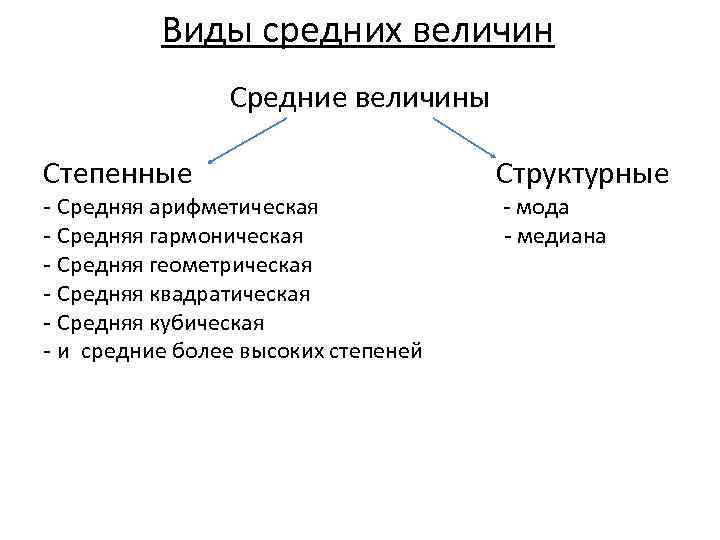
Виды средних величин Средние величины Степенные - Средняя арифметическая - Средняя гармоническая - Средняя геометрическая - Средняя квадратическая - Средняя кубическая - и средние более высоких степеней Структурные - мода - медиана

Средняя арифметическая 1)Простая. Применяется в случаях, когда имеются отдельные значения признака, т. е. данные не сгруппированы. (хi-значение признака, n – число наблюдений) 2)Взвешенная. Применяется в случаях, когда данные представлены в виде рядов распределения или группировок. Одни и те же значения признака повторяются несколько раз. (хi-значение признака, fi- вес (число повторений значений признака))

Студент сдал зимнюю сессию и получил следующие оценки на экзаменах: • Математика-4, • Макроэкономика-5, • Физкультура – 5, • Статистика- 3. Определить среднюю оценку студента. Решение: Средняя оценка рассчитывается по формуле средней арифметической простой, т. е.

Статистика футбольных матчей премьер-лиги России по числу забитых обеими командами мячей в 2010 г. имеет вид: Число забитых мячей 0 1 2 3 4 5 6 7 8 Всего Число матчей 27 54 61 48 26 14 4 5 1 240 Рассчитать среднее число мячей, забитых за одну игру. Решение: Число мячей - осредняемый признак (хi), Число матчей – вес признака (fi). Поскольку данные задачи сгруппированы, т. е. каждый признак xi имеет различную частоту повторений (fi), для расчет средней следует использовать среднюю арифметическую взвешенную:
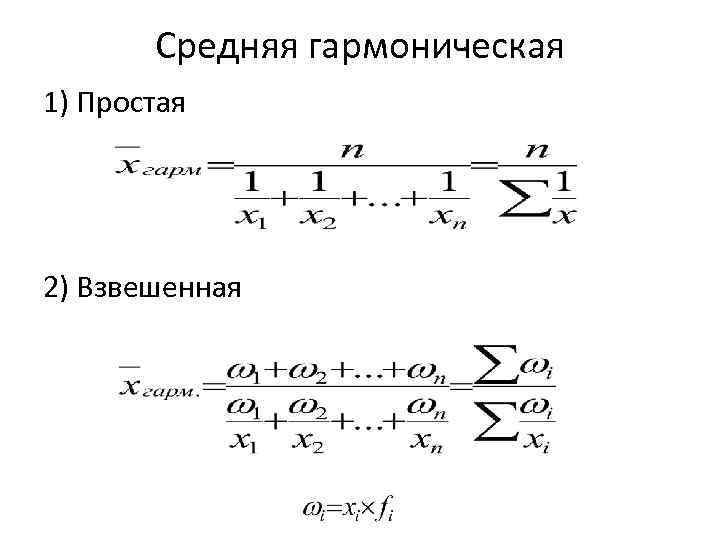
Средняя гармоническая 1) Простая 2) Взвешенная
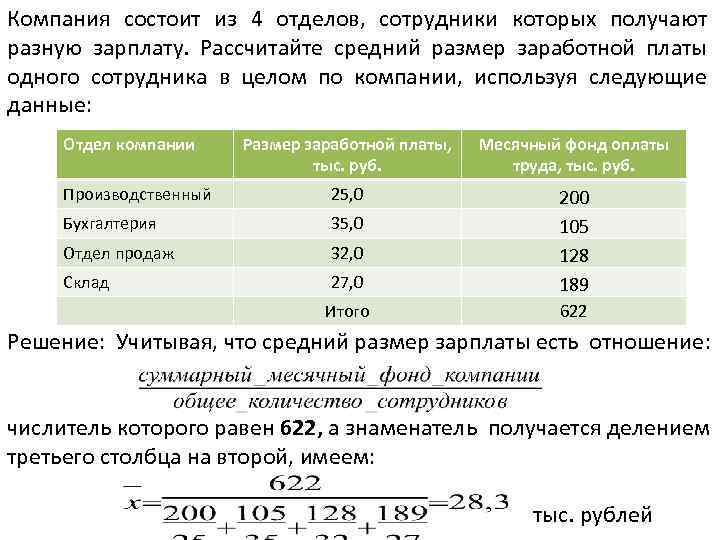
Компания состоит из 4 отделов, сотрудники которых получают разную зарплату. Рассчитайте средний размер заработной платы одного сотрудника в целом по компании, используя следующие данные: Отдел компании Размер заработной платы, тыс. руб. Месячный фонд оплаты труда, тыс. руб. Производственный 25, 0 Бухгалтерия 35, 0 Отдел продаж 32, 0 Склад 27, 0 200 105 128 189 Итого 622 Решение: Учитывая, что средний размер зарплаты есть отношение: числитель которого равен 622, а знаменатель получается делением третьего столбца на второй, имеем: тыс. рублей

Средняя геометрическая величина наиболее часто используются для определения среднего темпа роста экономических показателей (ВВП, инфляции, объема производства). 1) Простая 2) Взвешенная
Статистика.3..pptx