Системы счисления (часть 2) Подготовил : Ганбаров Анар


















okladnikova_agu_chasty_2.pptx
- Размер: 335.6 Кб
- Автор:
- Количество слайдов: 26
Описание презентации Системы счисления (часть 2) Подготовил : Ганбаров Анар по слайдам
 Системы счисления (часть 2) Подготовил : Ганбаров Анар Группа: ИТ 11 АГУ г. Астрахань
Системы счисления (часть 2) Подготовил : Ганбаров Анар Группа: ИТ 11 АГУ г. Астрахань
 Представление чисел в разрядной сетке ЭВМ
Представление чисел в разрядной сетке ЭВМ
 Представление чисел в разрядной сетке ЭВМ С фиксированной точкой (Целые числа) С плавающей точкой (Дробные числа)
Представление чисел в разрядной сетке ЭВМ С фиксированной точкой (Целые числа) С плавающей точкой (Дробные числа)
 С фиксированной точкой (Целые числа)
С фиксированной точкой (Целые числа)
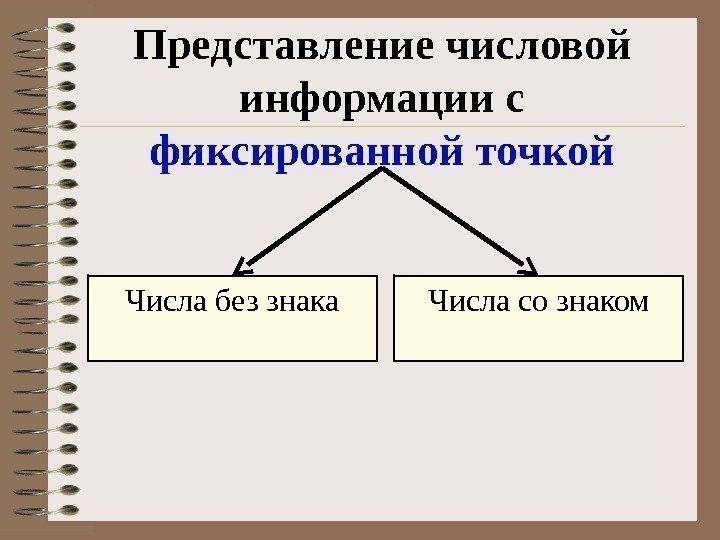
 Представление числовой информации с фиксированной точкой Числа со знаком. Числа без знака
Представление числовой информации с фиксированной точкой Числа со знаком. Числа без знака
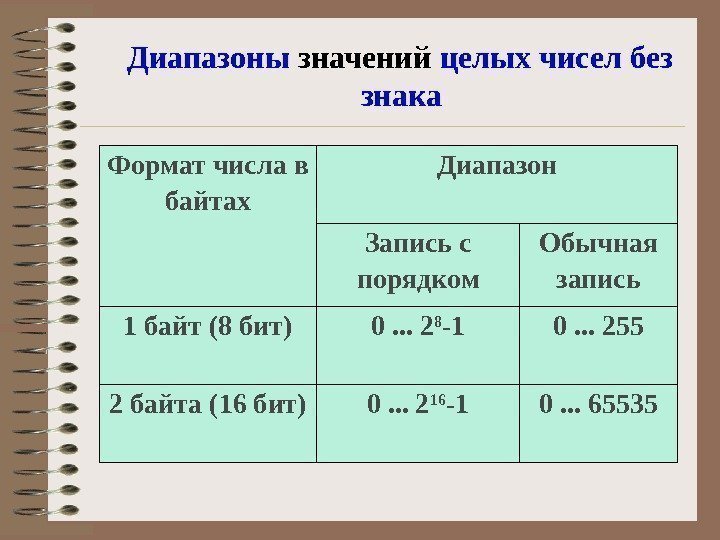
 Диапазоны значений целых чисел без знака Формат числа в байтах Диапазон Запись с порядком Обычная запись 1 байт (8 бит) 0. . . 2 8 -1 0. . . 255 2 байта (16 бит) 0. . . 2 16 -1 0. . .
Диапазоны значений целых чисел без знака Формат числа в байтах Диапазон Запись с порядком Обычная запись 1 байт (8 бит) 0. . . 2 8 -1 0. . . 255 2 байта (16 бит) 0. . . 2 16 -1 0. . .
 Примеры: Число 39 10 = 100111 2 в однобайтовом формате: Число 39 10 = 100111 2 в двубайтовом формате: Число 65 535 10 = 11111111 2 в двубайтовом формате:
Примеры: Число 39 10 = 100111 2 в однобайтовом формате: Число 39 10 = 100111 2 в двубайтовом формате: Число 65 535 10 = 11111111 2 в двубайтовом формате:
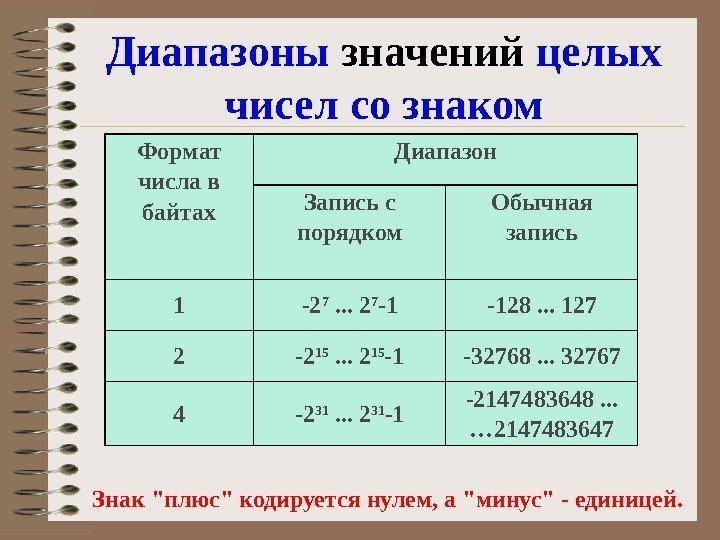
 Диапазоны значений целых чисел со знаком Формат числа в байтах Диапазон Запись с порядком Обычная запись 1 -2 7 . . . 2 7 -1 -128. . . 127 2 -2 15 . . . 2 15 -1 -32768. . . 32767 4 -2 31 . . . 2 31 -1 -2147483648. . . … 2147483647 Знак «плюс» кодируется нулем, а «минус» — единицей.
Диапазоны значений целых чисел со знаком Формат числа в байтах Диапазон Запись с порядком Обычная запись 1 -2 7 . . . 2 7 -1 -128. . . 127 2 -2 15 . . . 2 15 -1 -32768. . . 32767 4 -2 31 . . . 2 31 -1 -2147483648. . . … 2147483647 Знак «плюс» кодируется нулем, а «минус» — единицей.
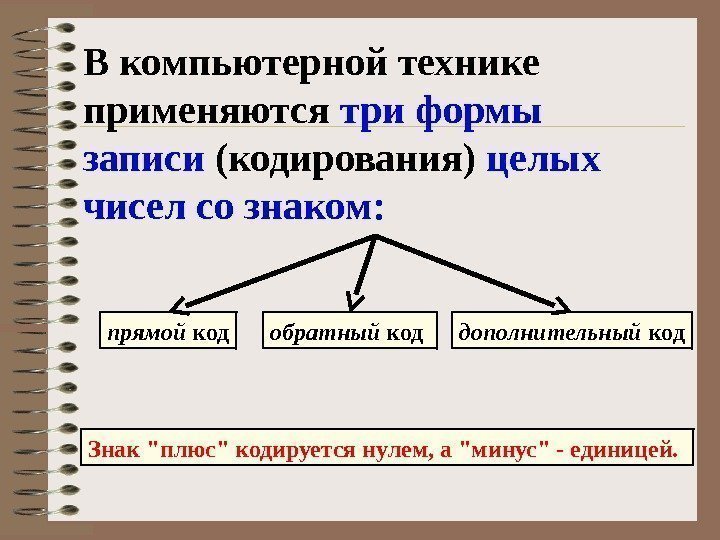
 В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код обратный код дополнительный код Знак «плюс» кодируется нулем, а «минус» — единицей.
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код обратный код дополнительный код Знак «плюс» кодируется нулем, а «минус» — единицей.
 Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде. Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение. 1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины
Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде. Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение. 1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины
 2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы –нулями. 3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы –нулями. 3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
 Пример: Число +7. Найти его прямой, обратный и дополнительный код. Так как число положительное, то прямой, обратный и дополнительный код будут одинаковыми и будут равны прямому коду. 0 1 1 1 Прямой 0 1 1 1 Обратный 0 1 1 1 Дополнительный Знак Число
Пример: Число +7. Найти его прямой, обратный и дополнительный код. Так как число положительное, то прямой, обратный и дополнительный код будут одинаковыми и будут равны прямому коду. 0 1 1 1 Прямой 0 1 1 1 Обратный 0 1 1 1 Дополнительный Знак Число
 Пример: Число -7. Найти его прямой, обратный и дополнительный код. Так как число отрицательное , то прямой, обратный и дополнительный код будут разными. Прямой код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 0 1 1 1 Число +7 2) А потом в знаковый разряд помещаем цифру 1. 1 1 Число -7 Прямой код
Пример: Число -7. Найти его прямой, обратный и дополнительный код. Так как число отрицательное , то прямой, обратный и дополнительный код будут разными. Прямой код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 0 1 1 1 Число +7 2) А потом в знаковый разряд помещаем цифру 1. 1 1 Число -7 Прямой код
 Пример(продолжение): Обратный код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 0 1 1 1 Число +7 2) Инвертируем все цифры двоичного кода , включая знаковую цифру. 1 0 0 0 Число -7 Обратный код
Пример(продолжение): Обратный код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 0 1 1 1 Число +7 2) Инвертируем все цифры двоичного кода , включая знаковую цифру. 1 0 0 0 Число -7 Обратный код
 Пример(продолжение): Дополнительный код 1) Берём обратный код. 1 0 0 0 Число -7 Обратный код 2) Прибавляем к нему единицу. К младшему разряду. (прибавляем единицу справа с конца) 1 0 0 0 Число -7 Обратный код + 1 1 0 0 1 Число -7 Дополнительный код
Пример(продолжение): Дополнительный код 1) Берём обратный код. 1 0 0 0 Число -7 Обратный код 2) Прибавляем к нему единицу. К младшему разряду. (прибавляем единицу справа с конца) 1 0 0 0 Число -7 Обратный код + 1 1 0 0 1 Число -7 Дополнительный код
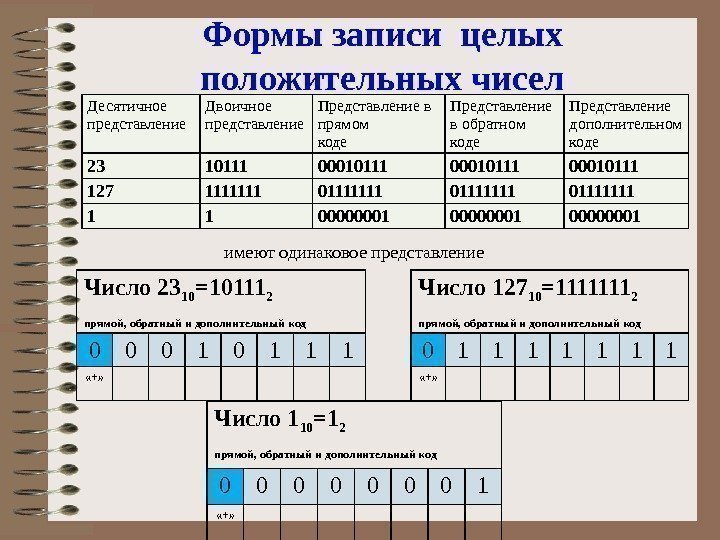
 Формы записи целых положительных чисел Десятичное представление Двоичное представление Представление в прямом коде Представление в обратном коде Представление дополнительном коде 23 10111 00010111 127 1111111 01111111 1 1 00000001 Число 23 10 =10111 2 прямой, обратный и дополнительный код 0 0 0 1 1 1 «+» Число 127 10 =1111111 2 прямой, обратный и дополнительный код 0 1 1 1 1 «+» имеют одинаковое представление Число 1 10 =1 2 прямой, обратный и дополнительный код 0 0 0 0 1 «+»
Формы записи целых положительных чисел Десятичное представление Двоичное представление Представление в прямом коде Представление в обратном коде Представление дополнительном коде 23 10111 00010111 127 1111111 01111111 1 1 00000001 Число 23 10 =10111 2 прямой, обратный и дополнительный код 0 0 0 1 1 1 «+» Число 127 10 =1111111 2 прямой, обратный и дополнительный код 0 1 1 1 1 «+» имеют одинаковое представление Число 1 10 =1 2 прямой, обратный и дополнительный код 0 0 0 0 1 «+»
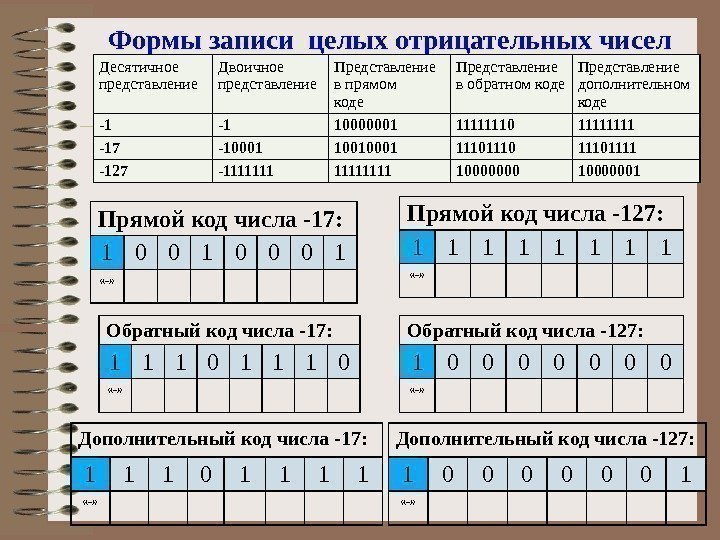
 Формы записи целых отрицательных чисел Десятичное представление Двоичное представление Представление в прямом коде Представление в обратном коде Представление дополнительном коде -1 -1 10000001 11111110 1111 -17 -10001 10010001 11101111 -127 -1111111 10000000 10000001 Прямой код числа -17: 1 0 0 0 1 «-» Прямой код числа -127: 1 1 1 1 «-» Обратный код числа -17: 1 1 1 0 «-» Обратный код числа -127: 1 0 0 0 0 «-» Дополнительный код числа -17: 1 1 1 0 1 1 «-» Дополнительный код числа -127: 1 0 0 0 1 «-»
Формы записи целых отрицательных чисел Десятичное представление Двоичное представление Представление в прямом коде Представление в обратном коде Представление дополнительном коде -1 -1 10000001 11111110 1111 -17 -10001 10010001 11101111 -127 -1111111 10000000 10000001 Прямой код числа -17: 1 0 0 0 1 «-» Прямой код числа -127: 1 1 1 1 «-» Обратный код числа -17: 1 1 1 0 «-» Обратный код числа -127: 1 0 0 0 0 «-» Дополнительный код числа -17: 1 1 1 0 1 1 «-» Дополнительный код числа -127: 1 0 0 0 1 «-»
 С плавающей точкой (Дробные числа)
С плавающей точкой (Дробные числа)
 Представление чисел с плавающей точкой. Этот способ представления опирается на нормализованную ( экспоненциальную ) запись действительных чисел. Нормализованная запись отличного от нуля действительного числа A — это запись вида: где m – мантисса числа (правильная дробь, у которой первая цифра после запятой не равна нулю), q – основание системы, n – порядок числа. •
Представление чисел с плавающей точкой. Этот способ представления опирается на нормализованную ( экспоненциальную ) запись действительных чисел. Нормализованная запись отличного от нуля действительного числа A — это запись вида: где m – мантисса числа (правильная дробь, у которой первая цифра после запятой не равна нулю), q – основание системы, n – порядок числа. •
 Примеры: 1. Мантисса числа 64. 5 – это число 0. 645, а порядок – число 2, так как 64. 5 = 0. 645*10 степень (2). 2. Мантисса числа 0. 0000012 – это число 0. 12, а порядок – число -5, потому что 0. 0000012= =0. 12*10 степень(-5). При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды — для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы.
Примеры: 1. Мантисса числа 64. 5 – это число 0. 645, а порядок – число 2, так как 64. 5 = 0. 645*10 степень (2). 2. Мантисса числа 0. 0000012 – это число 0. 12, а порядок – число -5, потому что 0. 0000012= =0. 12*10 степень(-5). При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды — для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы.
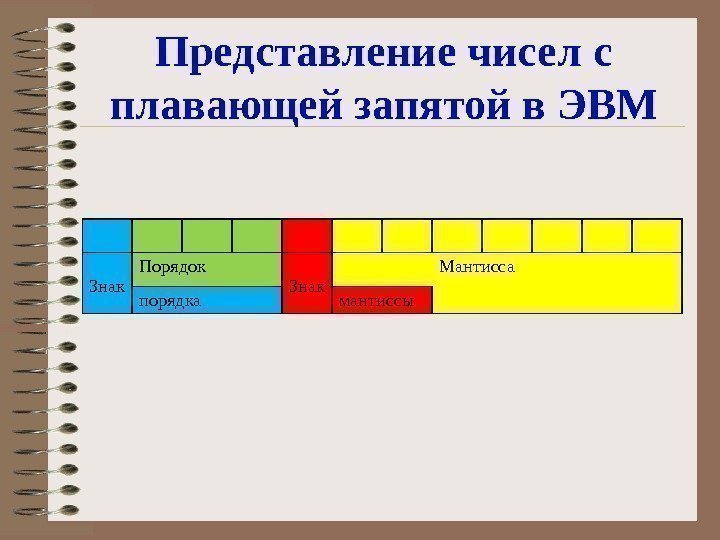
 Представление чисел с плавающей запятой в ЭВМ Знак Порядок Знак Мантисса порядка мантиссы
Представление чисел с плавающей запятой в ЭВМ Знак Порядок Знак Мантисса порядка мантиссы
 Пример: Изобразить число 65 в 12 -ти разрядной сетке. Мантисса числа 64. 5 – это число 0. 645=0, 1010010 Порядок – число (), так как 64. 5 = 0. 645*10 степень (2). Знак мантиссы и порядка « + » , который обозначается через нуль в двоичном коде. • 0 0 1 0 1 0 Знак Порядок Знак Мантисса порядка мантиссы
Пример: Изобразить число 65 в 12 -ти разрядной сетке. Мантисса числа 64. 5 – это число 0. 645=0, 1010010 Порядок – число (), так как 64. 5 = 0. 645*10 степень (2). Знак мантиссы и порядка « + » , который обозначается через нуль в двоичном коде. • 0 0 1 0 1 0 Знак Порядок Знак Мантисса порядка мантиссы
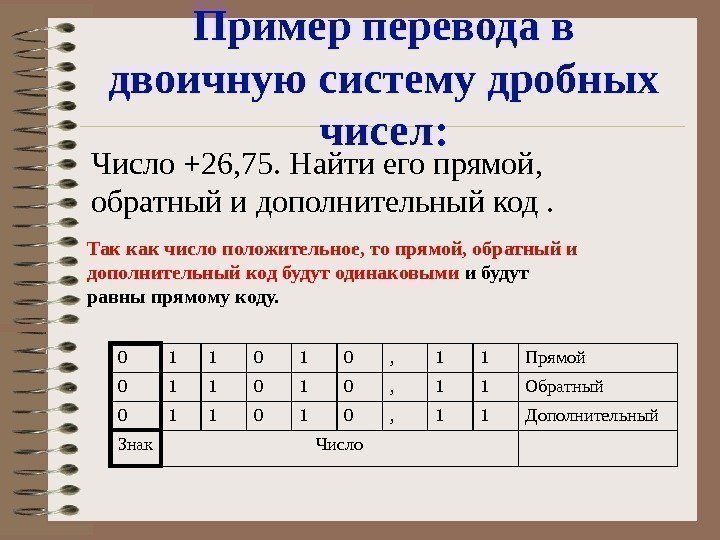
 Пример перевода в двоичную систему дробных чисел: Число +26, 75. Найти его прямой, обратный и дополнительный код. Так как число положительное, то прямой, обратный и дополнительный код будут одинаковыми и будут равны прямому коду. 0 1 1 0 , 1 1 Прямой 0 1 1 0 , 1 1 Обратный 0 1 1 0 , 1 1 Дополнительный Знак Число
Пример перевода в двоичную систему дробных чисел: Число +26, 75. Найти его прямой, обратный и дополнительный код. Так как число положительное, то прямой, обратный и дополнительный код будут одинаковыми и будут равны прямому коду. 0 1 1 0 , 1 1 Прямой 0 1 1 0 , 1 1 Обратный 0 1 1 0 , 1 1 Дополнительный Знак Число
 Пример: Число -26, 75. Найти его прямой, обратный и дополнительный код. Так как число отрицательное , то прямой, обратный и дополнительный код будут разными. Прямой код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 2) А потом в знаковый разряд помещаем цифру 1. 0 1 1 0 , 1 1 Число +26, 75 1 1 1 0 , 1 1 Число -26,
Пример: Число -26, 75. Найти его прямой, обратный и дополнительный код. Так как число отрицательное , то прямой, обратный и дополнительный код будут разными. Прямой код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 2) А потом в знаковый разряд помещаем цифру 1. 0 1 1 0 , 1 1 Число +26, 75 1 1 1 0 , 1 1 Число -26,
 Пример(продолжение): Обратный код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 2) Инвертируем все цифры двоичного кода , включая знаковую цифру. 0 1 1 0 , 1 1 Число +26, 75 1 0 0 1 , 0 0 Число -26, 75 Обратный
Пример(продолжение): Обратный код : 1) Сначала находим код |модуля| этого числа, то есть код этого же числа , только со знаком «+» 2) Инвертируем все цифры двоичного кода , включая знаковую цифру. 0 1 1 0 , 1 1 Число +26, 75 1 0 0 1 , 0 0 Число -26, 75 Обратный
 Пример(продолжение): Дополнительный код 1) Берём обратный код. 2) Прибавляем к нему единицу. К младшему разряду. (прибавляем единицу справа с конца)1 0 0 1 0 1 , 0 0 Число -26, 75 Обратный + 1 1 0 0 1 , 0 1 Число -26, 75 Дополн.
Пример(продолжение): Дополнительный код 1) Берём обратный код. 2) Прибавляем к нему единицу. К младшему разряду. (прибавляем единицу справа с конца)1 0 0 1 0 1 , 0 0 Число -26, 75 Обратный + 1 1 0 0 1 , 0 1 Число -26, 75 Дополн.
