Система векторов называется базисом пространства R n ,

Система векторов называется базисом пространства R n , если 1 Векторы этой системы линейно независимы. 2 Любой вектор из этого пространства линейно выражается через векторы этой системы.

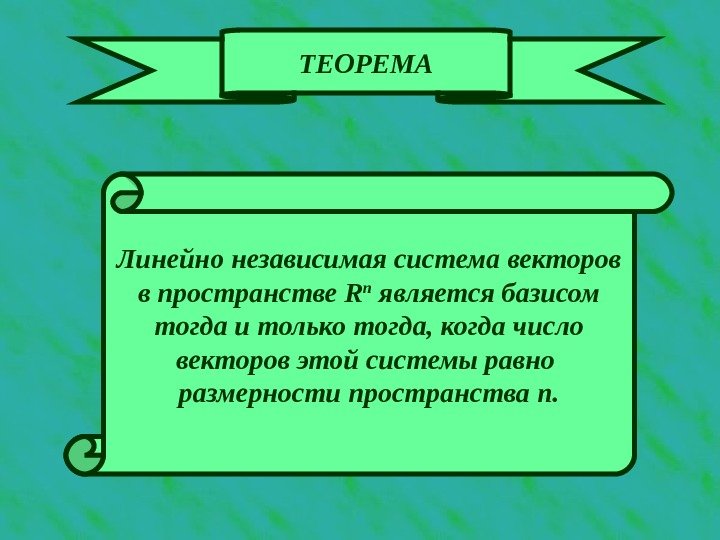
ТЕОРЕМА Линейно независимая система векторов в пространстве R n является базисом тогда и только тогда, когда число векторов этой системы равно размерности пространства n.

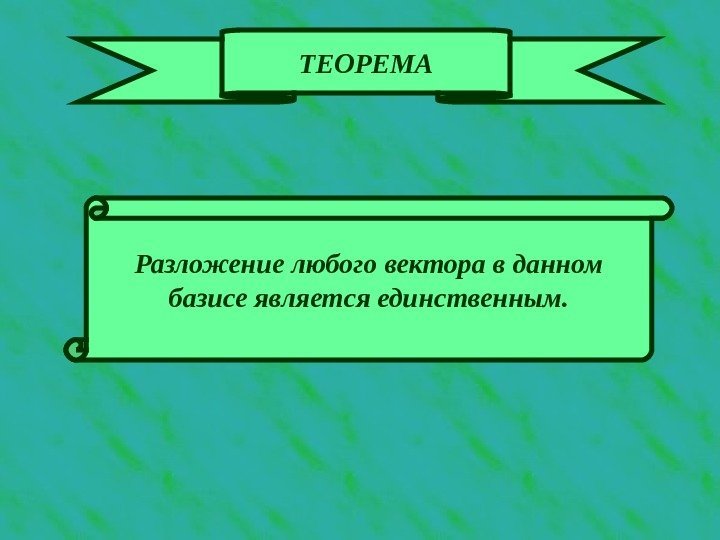
ТЕОРЕМА Разложение любого вектора в данном базисе является единственным.

Пусть система векторов ДОКАЗАТЕЛЬСТВО: naaa . . . , 21 является базисом. Предположим, что вектор b может быть представлен в виде линейной комбинации базисных векторов двумя способами: nnaaab . . .

Причем наборы чисел Получили, что линейная комбинация векторов системы равна нулю, т. е. Система оказалась линейно зависимой, что противоречит условию теоремы. n. . . , 21 иn. . . , 21 не совпадают. Вычтем одно равенство из другого: 0)(. . . )()(222111 nnnaaa Следовательно, разложение вектора в данном базисе будет единственным.

Таким образом, в произвольном базисе пространства R n любой вектор из этого пространства представим в виде разложения по базисным векторам: Причем, это разложение является единственным для данного базиса. nnaaab . . . 2211 Числа n. . . , 21 называются координатами вектора b в базисе naaa . . . ,

Чтобы найти коэффициенты разложения α i в случае произвольного базиса, нужно приравнять соответствующие координаты линейной комбинации и координаты вектора Пусть базисные вектора заданы в координатной форме: И задан вектор b ). . . , (. . . ). . . , ( 21 112111 nnnnn n aaaa ). . . , (21 nbbbb

Тогда получим систему линейных уравнений: Решая эту систему, находим коэффициенты разложения nnnnnn nn nn baaa . . . 2211 22222211 11122111 n. . . ,

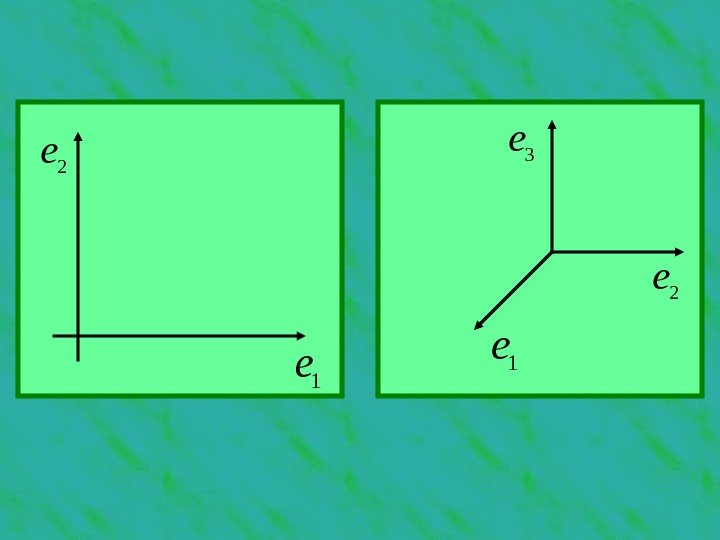
Рассмотрим базис пространства R n , в котором каждый вектор ортогонален остальным векторам базиса: Такой базис называется ортогональным. Они хорошо представимы на плоскости и в пространстве: neee . . . , 21 0), ( ji ee njiji. . . 2, 1,

1 e 1 e 2 e 2 e 3 e

Найдем разложение вектора в ортогональном базисе: Умножим обе части равенства на b nn eeeb . . . 2211 1 e ), (. . . ), (), (11221111 eeeeeeebnn Поскольку все вектора базиса взаимно ортогональны, то 0), ( ji ee ji

Имеем: В общем случае: ), ( 1111 eeeb 2 1 1 1 ), ( e eb ee eb 2 ), ( i i i e eb

Частным случаем ортогонального базиса является ортонормированный базис. В этом случае все базисные вектора имеют единичную длину: 1 ie Тогда коэффициенты разложения имеют вид: ), ( ii eb ni. . . 2,