Симплекс-метод решения задачи ЛП Лекция 3 Идея

Симплекс-метод решения задачи ЛП Лекция 3

Идея симплекс-метода n n Возвратимся к общему случаю: Предположим, что в системе ограничений какие-либо k неизвестных выбраны в качестве свободных. Из линейной алгебры известно, что им можно придавать произвольные значения, а значения остальных (базисных) переменных найти из решения системы (1). Каждому выбору свободных неизвестных отвечает своё базисное решение. В качестве примера рассмотрим задачу 1: В качестве целевой функции рассматриваем:

Преобразование системы ограничений в виде неравенств в систему ограничений равенств n Система ограничений равенств:

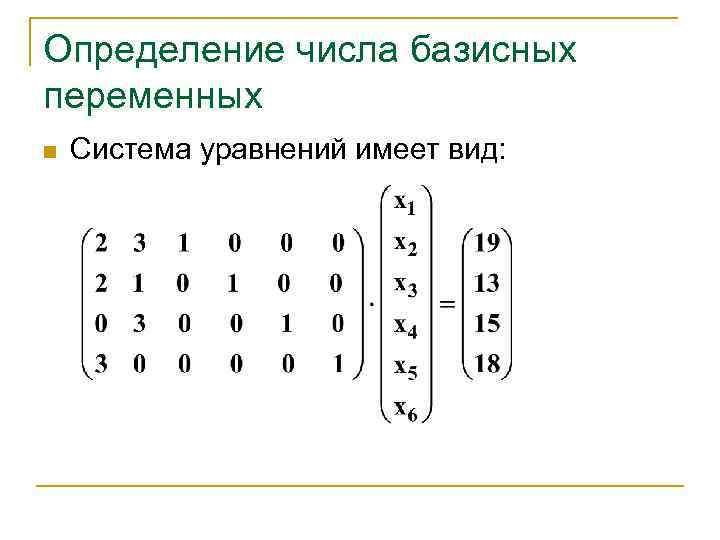Определение числа базисных переменных n Система уравнений имеет вид:

Определение базисных и свободных переменных n Отсюда видно, что данная система уравнений имеет ранг, равный 4, т. к. максимальный порядок минора, отличного от нуля равен 4. Значит в качестве базисных неизвестных можно брать а в качестве свободных соответственно:

Формулировка задачи n Система ограничений: Если в качестве свободных неизвестных выбрать , то получим базисное решение:

Дальнейшие действия n В выражении , неизвестные входят с отрицательным знаком, поэтому их дальнейшее увеличение вызывает уменьшение значения формы , поэтому увеличиваем значение, например, а оставляем неизменной. Неизвестная может возрастать до значения , тогда как другая переменная остаётся , при этом все остальные положительными.

Суть метода последовательного изменения базисных переменных n n Выберем теперь новую пару свободных неизвестных , оставляя при этом : Далее выразим базисные неизвестные через свободные из системы уравнений:

Суть метода последовательного изменения базисных переменных n Допустимым базисным решением является решение: В выражении целевой функции свободная неизвестная входит с отрицательным знаком, поэтому, увеличивая её, можем только уменьшить значение. Увеличить значение можем не более, чем до значения. При этом ,

Суть метода последовательного изменения базисных переменных n Остальные же значения базисных переменных остаются положительными: Примем теперь за свободные переменные. Выразим через них значения целевой функции и базисных неизвестных:

Суть метода последовательного изменения базисных переменных n Получаем новую форму связи переменных и значение целевой функции:

Суть метода последовательного изменения базисных переменных n Далее увеличиваем значение переменной. Соответствующее базисное решение будет: Далее принимаем за свободные неизвестные и выражая базисные через них, получим:

Завершающий этап n Тогда получим: Свободные переменные теперь входят в целевую функцию со знаком +, тогда дальнейшее уменьшение целевой функции не возможно за счёт их изменения. Т. о. имеем оптимальный план.

Алгебра симплекс-метода n Пусть система ограничений и целевая функция основной ЛП имеют вид: (1) (2)

Идея СМ n Предположим, что ранг системы (1) меньше числа неизвестных: . Всегда можно занумеровать неизвестные так, чтобы свободными оказались первые неизвестные: . Выражая в этом случае базисные (несвободные) неизвестные , приходим к известным соотношениям:

Идея СМ n Получаем систему: (1) и соответствующую целевую функцию (2):

Идея СМ Базисное решение, отвечающее данному выбору свободных неизвестных таково: (3) Пусть решение (3) является допустимым. Это означает, что все и форма при этом: . Покажем, как от допустимого базисного решения (3) перейти к другому базисному решению, при котором форма , имеет значение меньшее, чем первоначальное. n

Идея СМ n Для упрощения последующих выкладок, перепишем систему (1) и соответствующую форму (2)в виде:

Идея СМ n Далее переобозначим: приводим систему и целевую функцию к виду: (3) (4)

Идея СМ n Замечание: Во всех случаях при работе по симплекс-методу мы должны записывать систему ограничений и минимизирующую форму в виде (3), (4). Такая запись требует, чтобы перед группой слагаемых, содержащих свободные неизвестные, выставлялся общий знак минус.

Идея СМ Сведём все коэффициенты при свободных неизвестных и свободные члены из (3) и (4) в общую таблицу, которую назовём Симплекс-таблицей. Каждая строка отвечает соответствующему уравнению. 1. Рассмотрим те из свободных неизвестных, которые входят в выражение (4) формы F с положительными коэффициентами. Выберем среди рассмотренных неизвестных одну, например, . n

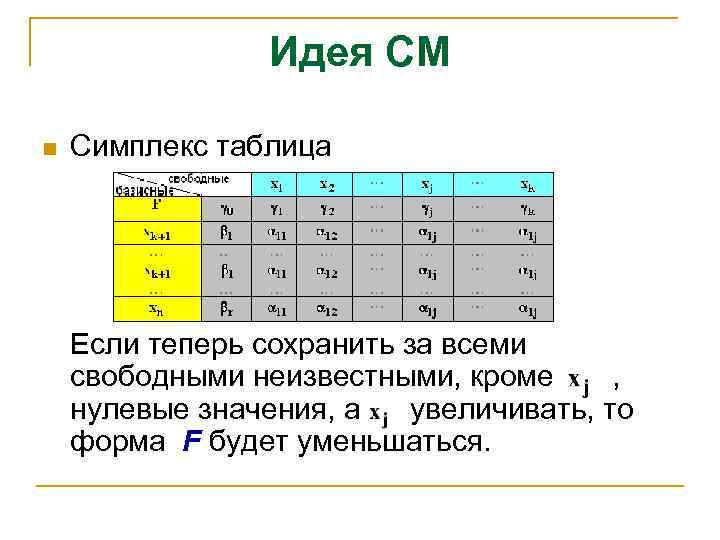Идея СМ n Симплекс таблица Если теперь сохранить за всеми свободными неизвестными, кроме , нулевые значения, а увеличивать, то форма F будет уменьшаться.

Идея СМ n Известно, что можем увеличивать до тех пор, пока впервые не обратится в « 0» какая-либо из базисных неизвестных Когда это может произойти? Рассмотрим систему (3) и в ней полагаем: Тогда, будем иметь:

Идея СМ n Учитывая, что в следующей зависимости: (*) Из (*)ясно, что базисная неизвестная (**) при

Идея СМ n Выбирая среди всех соотношений (**) наименьшее, и пусть оно отвечает индексу , т. е. Тогда ясно, что при возрастании значения от нулевого значения первой обратится в « 0» именно базисная неизвестная. При этом остальные базисные неизвестные всё ещё остаются положительными.

Идея СМ Коэффициент играет важную роль в дальнейших преобразованиях и называется генеральным. 2. Выведем неизвестную из числа свободных неизвестных (сделаем её базисной), а вместо в число свободных неизвестных введём базисную. В остальном наборы базисных и свободных неизвестных сохраняются. n

Идея СМ n Из l-того уравнения системы (3)выражаем переменную : Для того, чтобы выразить остальные новые базисные неизвестные через новые свободные подставим полученное выражение из (5) в уравнения системы (3). При этом все коэффициенты меняются по одному закону.

Идея СМ n n Полагая новые свободные неизвестные равными нулю, находим новое базисное решение и соответствующее ему новое значение формы. Отсюда правила работы с симплекстаблицей:

Правила работы с симплекстаблицей (пункт 1) 1). Выбираем генеральный элемент , находим ему обратный и вносим его в нижнее отделение клетки, содержащей генеральный элемент.

Правила работы с симплекстаблицей (пункт 2) 2). Умножаем на значение все коэффициенты (кроме ) из верхних ячеек - той строки и поместим полученные произведения в соответствующие нижние ячейки этой же строки.

Правила работы с симплекстаблицей (пункт 3) 3). Умножаем на все коэффициенты (кроме ) из верхних ячеек того столбца и поместим полученные произведения в соответствующие нижние ячейки этого же столбца той строки.

Правила работы с симплекстаблицей (пункт 4, 5) 4). Выделяем числа, расположенные в верхних ячейках , ав том столбце – числа в нижних ячейках каждой клетки. 5). Число, вносимое в нижнюю ячейку клетки на пересечении ой строки и того столбца ( ), находим перемножением записанных (выделенных) чисел из той же ой строки и того же того столбца. Далее переход к табл. 2

Правила работы с симплекс-таблицей (пункты 6, 7)(переход к таблице 2) 6). Во все верхние ячейки - той строки и того столбца табл. 2 поместим числа из соответствующих нижних ячеек из табл. 1. 7). В каждую верхнюю ячейку остальных клеток поместим число, равное сумме чисел из верхней и нижней ячеек соответствующей клетки табл. 1 (включая и форму ). И т. д. до решения ( ).

Работа с симплекс-таблицей (пример) n Рассмотрим задачу ЛП:

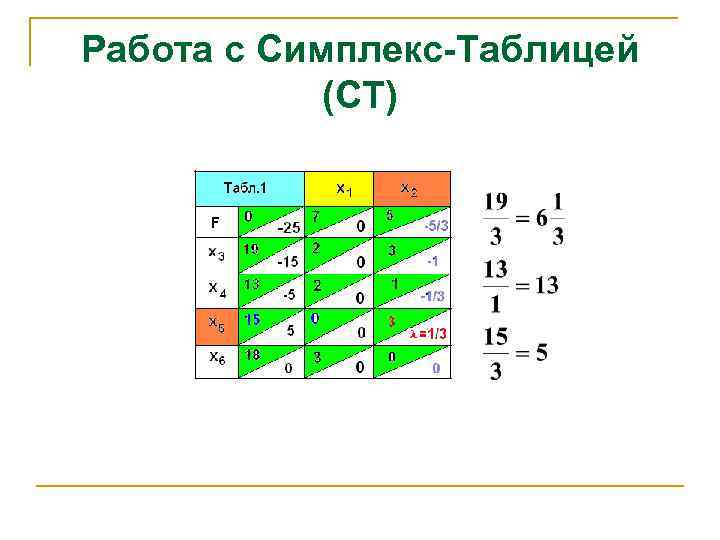Работа с Симплекс-Таблицей (СТ)

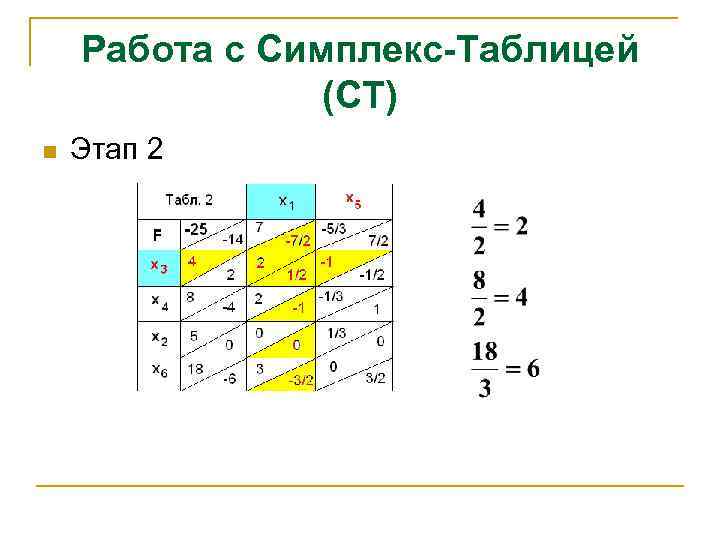Работа с Симплекс-Таблицей (СТ) n Этап 2

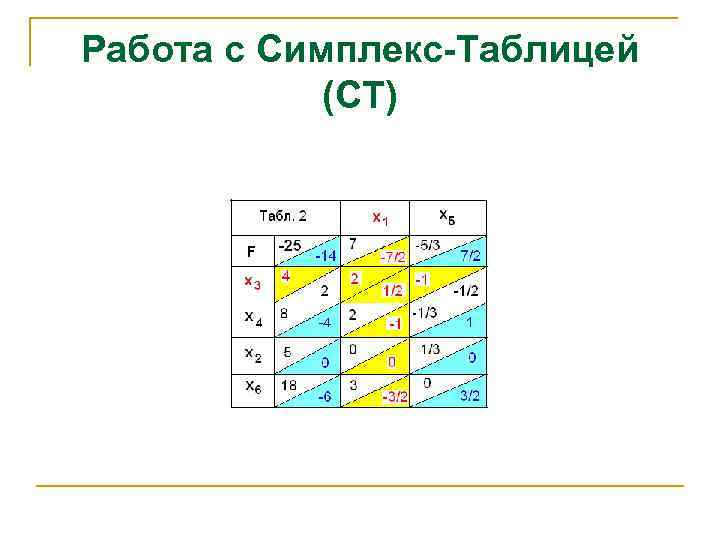Работа с Симплекс-Таблицей (СТ)

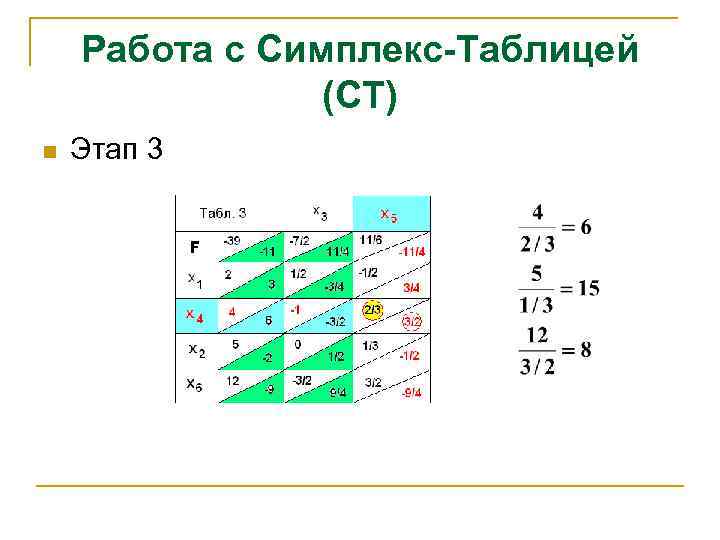Работа с Симплекс-Таблицей (СТ) n Этап 3

Работа с Симплекс-Таблицей (СТ) n Этап 4