Шотиди Константин Харлампиевич Литература: 1. Теоретические































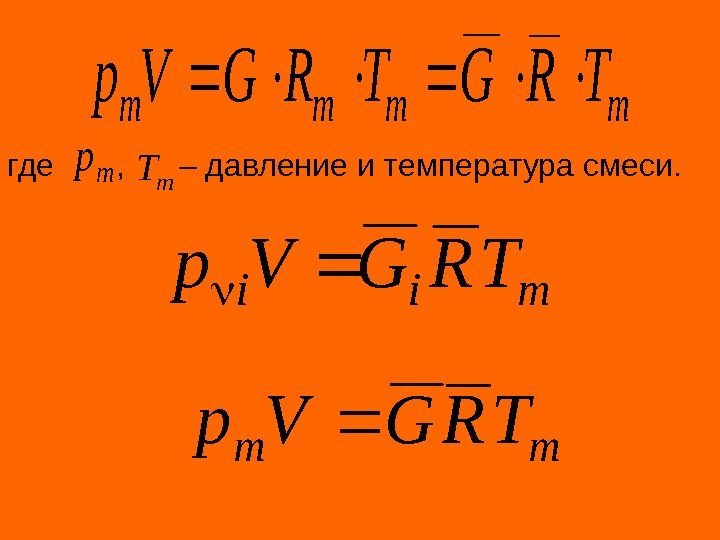
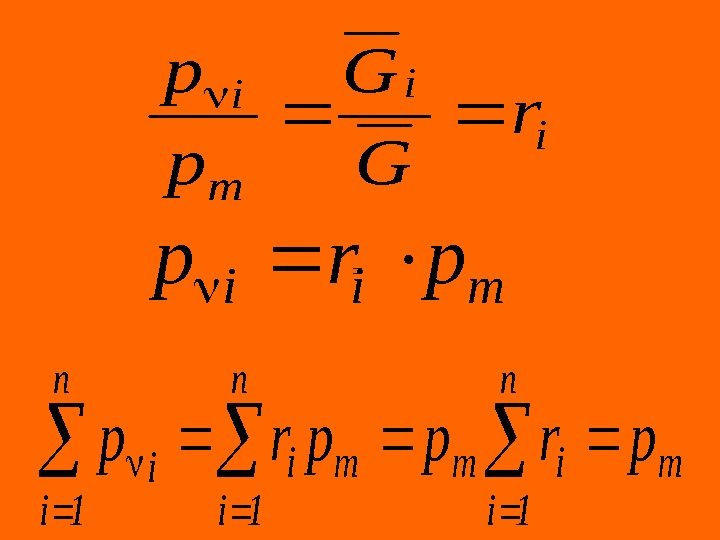














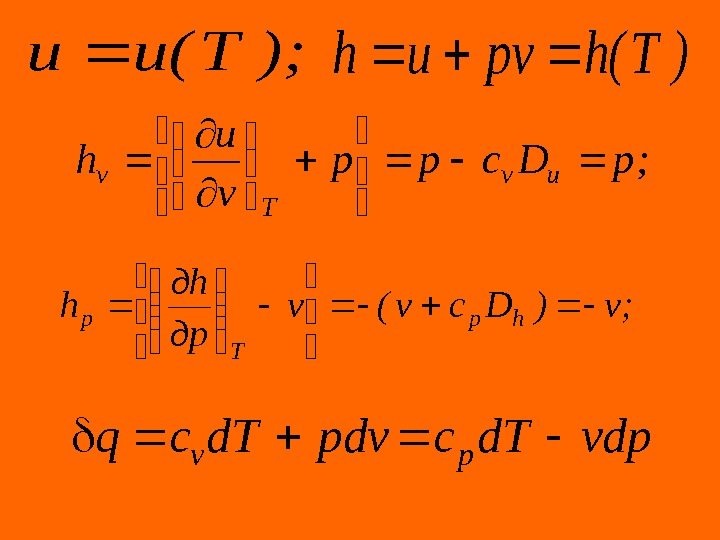






lekciya_1-3.ppt
- Размер: 2.5 Мб
- Автор: Anastasia Verteletskaya
- Количество слайдов: 62
Описание презентации Шотиди Константин Харлампиевич Литература: 1. Теоретические по слайдам
 Шотиди Константин Харлампиевич • Литература: • 1. Теоретические основы теплотехники: • часть первая «Техническая термодинамика, • Часть вторая «Теплопередача» , • Авторы: Поршаков Б. П. и др. • 2. Термодинамика и теплопередача. • Авторы: Поршаков Б. П. и др.
Шотиди Константин Харлампиевич • Литература: • 1. Теоретические основы теплотехники: • часть первая «Техническая термодинамика, • Часть вторая «Теплопередача» , • Авторы: Поршаков Б. П. и др. • 2. Термодинамика и теплопередача. • Авторы: Поршаков Б. П. и др.
 Правила рейтинга по курсу теплотехника для студентов факультета разработки нефтяных и газовых месторождений • Максимальное количество рейтинговых баллов за работу по основной программе в семестре 55, за ответ на экзамене 45. Итоговый рейтинговый балл вычисляется как сумма семестрового и экзаменационного баллов. • В зачетную книжку и в ведомость проставляется итоговая оценка, определяемая по итоговому баллу по схеме: [50 -74 – «удовл. » , [75 -89] – «хорошо» , [90 -100] – «отлично» .
Правила рейтинга по курсу теплотехника для студентов факультета разработки нефтяных и газовых месторождений • Максимальное количество рейтинговых баллов за работу по основной программе в семестре 55, за ответ на экзамене 45. Итоговый рейтинговый балл вычисляется как сумма семестрового и экзаменационного баллов. • В зачетную книжку и в ведомость проставляется итоговая оценка, определяемая по итоговому баллу по схеме: [50 -74 – «удовл. » , [75 -89] – «хорошо» , [90 -100] – «отлично» .
 • Семестровый рейтинговый балл складывается из выполнения и защиты лабораторных работ (до 30 баллов), результатов одной контрольной работы до 10 баллов, двух индивидуальных домашних работ (терм. 10 баллов, теплоп. 5 баллов), премиальных (бонусных) баллов, начисляемых за работу сверх программы. • Лабораторный практикум состоит из шести лабораторных работ оцениваемых максимальными баллами до 5. В случае пропуска по уважительной причине лабораторная работа может быть выполнена в течении двух недель на консультации. • Контрольная работа состоит из теоретического теста (пять вопросов) и двух задач. Максимальное количество баллов за контрольную работу до 10.
• Семестровый рейтинговый балл складывается из выполнения и защиты лабораторных работ (до 30 баллов), результатов одной контрольной работы до 10 баллов, двух индивидуальных домашних работ (терм. 10 баллов, теплоп. 5 баллов), премиальных (бонусных) баллов, начисляемых за работу сверх программы. • Лабораторный практикум состоит из шести лабораторных работ оцениваемых максимальными баллами до 5. В случае пропуска по уважительной причине лабораторная работа может быть выполнена в течении двух недель на консультации. • Контрольная работа состоит из теоретического теста (пять вопросов) и двух задач. Максимальное количество баллов за контрольную работу до 10.
 • Индивидуальное задание состоит из двух домашних заданий и оценивается первая максимум в 10 баллов, вторая 5 баллов при условии сдачи задания в срок. Опоздание на неделю уменьшает максимальный бал на два балла. • Премиальные баллы за работу вне программы начисляются: • За участие в университетской олимпиаде по термодинамике; • За выступление на конференции СНО с докладом по термодинамике. • Для получения зачета надо набрать семестровый рейтинг не меньше 30 баллов, при условии выполнения всех лабораторных работ (минимальное количество баллов 20). Студенты, не набравшие 30 баллов, могут довести свой балл до 30 в течение последней недели семестра.
• Индивидуальное задание состоит из двух домашних заданий и оценивается первая максимум в 10 баллов, вторая 5 баллов при условии сдачи задания в срок. Опоздание на неделю уменьшает максимальный бал на два балла. • Премиальные баллы за работу вне программы начисляются: • За участие в университетской олимпиаде по термодинамике; • За выступление на конференции СНО с докладом по термодинамике. • Для получения зачета надо набрать семестровый рейтинг не меньше 30 баллов, при условии выполнения всех лабораторных работ (минимальное количество баллов 20). Студенты, не набравшие 30 баллов, могут довести свой балл до 30 в течение последней недели семестра.
 • К экзамену допускаются студенты получившие зачет по теплотехнике и включенные деканатом в экзаменационную ведомость. Экзамен состоит из трех вопросов оцениваемый каждый до 15 Если студент набрал на экзамене меньше 25 баллов, то в ведомость ставится оценка «неуд. » (даже если суммарный рейтинговый балл больше 50).
• К экзамену допускаются студенты получившие зачет по теплотехнике и включенные деканатом в экзаменационную ведомость. Экзамен состоит из трех вопросов оцениваемый каждый до 15 Если студент набрал на экзамене меньше 25 баллов, то в ведомость ставится оценка «неуд. » (даже если суммарный рейтинговый балл больше 50).
 ТЕПЛОТЕХНИКА Теоретические основы Теплосиловое оборудование
ТЕПЛОТЕХНИКА Теоретические основы Теплосиловое оборудование
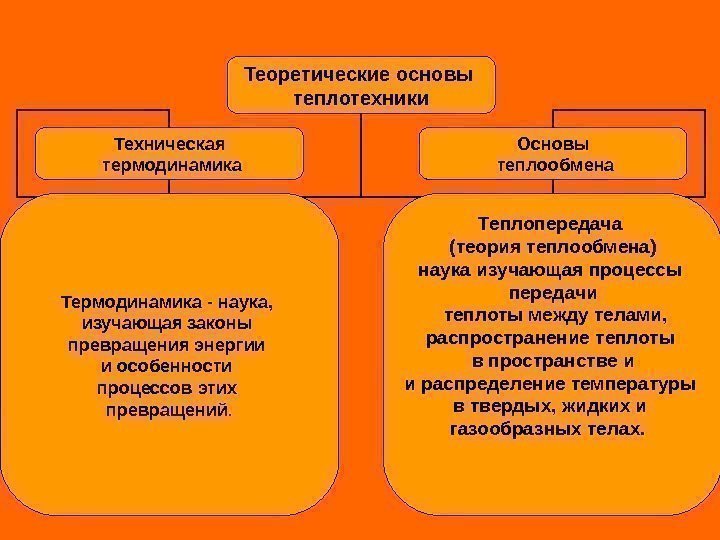
 Теоретические основы теплотехники Техническая термодинамика Основы теплообмена Термодинамика — наука, изучающая законы превращения энергии и особенности процессов этих превращений. Теплопередача (теория теплообмена) наука изучающая процессы передачи теплоты между телами, распространение теплоты в пространстве и и распределение температуры в твердых, жидких и газообразных телах.
Теоретические основы теплотехники Техническая термодинамика Основы теплообмена Термодинамика — наука, изучающая законы превращения энергии и особенности процессов этих превращений. Теплопередача (теория теплообмена) наука изучающая процессы передачи теплоты между телами, распространение теплоты в пространстве и и распределение температуры в твердых, жидких и газообразных телах.
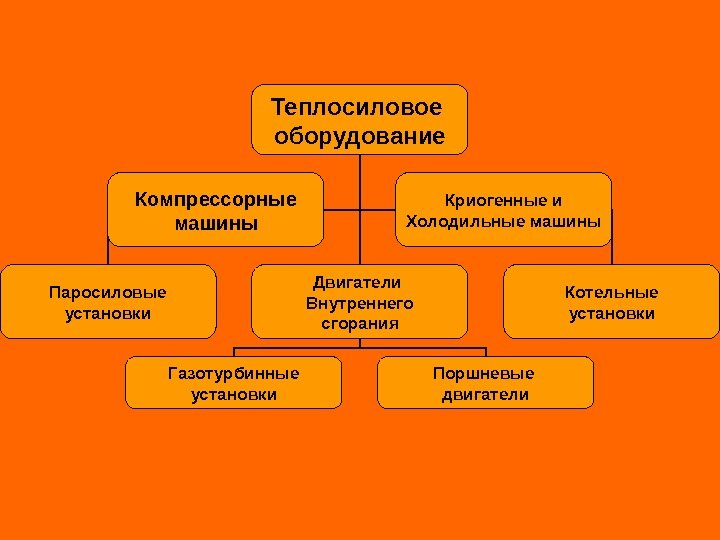
 Теплосиловое оборудование Паросиловые установки Двигатели Внутреннего сгорания Котельные установки. Компрессорные машины Криогенные и Холодильные машины Газотурбинные установки Поршневые двигатели
Теплосиловое оборудование Паросиловые установки Двигатели Внутреннего сгорания Котельные установки. Компрессорные машины Криогенные и Холодильные машины Газотурбинные установки Поршневые двигатели
 • Основные определения и понятия • Термодинамическая система Под понятием системы подразумевается тело или совокупность тел. Система называется закрытой, если она сохраняет постоянное количество вещества при всех происходящих в ней изменениях; если нет, то систему принято называть открытой. Если между системой и окружающей ее средой нет каких-либо энергетических взаимодействий (обмен работой и теплотой), то такую систему принято называть изолированной системой. Если отсутствует теплообмен систему называют адиабатический изолированной. .
• Основные определения и понятия • Термодинамическая система Под понятием системы подразумевается тело или совокупность тел. Система называется закрытой, если она сохраняет постоянное количество вещества при всех происходящих в ней изменениях; если нет, то систему принято называть открытой. Если между системой и окружающей ее средой нет каких-либо энергетических взаимодействий (обмен работой и теплотой), то такую систему принято называть изолированной системой. Если отсутствует теплообмен систему называют адиабатический изолированной. .
 Термодинамической системой принято называть закрытую систему, внутреннее состояние которой определяется значениями определенного количества независимых переменных, которые принято называть параметрами состояния. Если состояние термодинамической системы и ее параметры не изменяются во времени, то говорят, что система находится в равновесном состоянии. Равновесным состоянием системы называется такое тепловое, химическое, механическое состояние системы, которое может существовать сколь угодно долго при отсутствии внешнего воздействия. Простейшей термодинамической системой или простым телом называется система, физическое состояние которой вполне определяется значениями двух независимых переменных.
Термодинамической системой принято называть закрытую систему, внутреннее состояние которой определяется значениями определенного количества независимых переменных, которые принято называть параметрами состояния. Если состояние термодинамической системы и ее параметры не изменяются во времени, то говорят, что система находится в равновесном состоянии. Равновесным состоянием системы называется такое тепловое, химическое, механическое состояние системы, которое может существовать сколь угодно долго при отсутствии внешнего воздействия. Простейшей термодинамической системой или простым телом называется система, физическое состояние которой вполне определяется значениями двух независимых переменных.
 Идеальным газом называется система, физическое состояние которой вполне определяется значением одной независимой переменной, а именно значением абсолютной температурой ( T ). Параметры состояния — физические величины, характеризующие внутреннее состояние термодина-мической системы. К простейшим термодинамическим параметрам состояния относятся: удельный объем ( v ), давление ( p ) и температура ( T ). Связь между параметрами, характеризующими состояние простого тела, называется уравнением состояния F ( р, v , T ) = 0.
Идеальным газом называется система, физическое состояние которой вполне определяется значением одной независимой переменной, а именно значением абсолютной температурой ( T ). Параметры состояния — физические величины, характеризующие внутреннее состояние термодина-мической системы. К простейшим термодинамическим параметрам состояния относятся: удельный объем ( v ), давление ( p ) и температура ( T ). Связь между параметрами, характеризующими состояние простого тела, называется уравнением состояния F ( р, v , T ) = 0.
 Термодинамические процессы Изменение состояния системы называется процессом. Равновесный процесс — это непрерывная последо — вательность равновесных состояний системы. Обратимым процессом называется такой равно — весный процесс, который допускает возможность возврата этой системы из конечного состояния в исходное путем обратного процесса. В результате прямого и обратного обратимых процессов в системе и во внешней среде не происходит каких либо остаточных конечных изменений. Термодинамическим процессом принято считать обратимый равновесный процесс.
Термодинамические процессы Изменение состояния системы называется процессом. Равновесный процесс — это непрерывная последо — вательность равновесных состояний системы. Обратимым процессом называется такой равно — весный процесс, который допускает возможность возврата этой системы из конечного состояния в исходное путем обратного процесса. В результате прямого и обратного обратимых процессов в системе и во внешней среде не происходит каких либо остаточных конечных изменений. Термодинамическим процессом принято считать обратимый равновесный процесс.
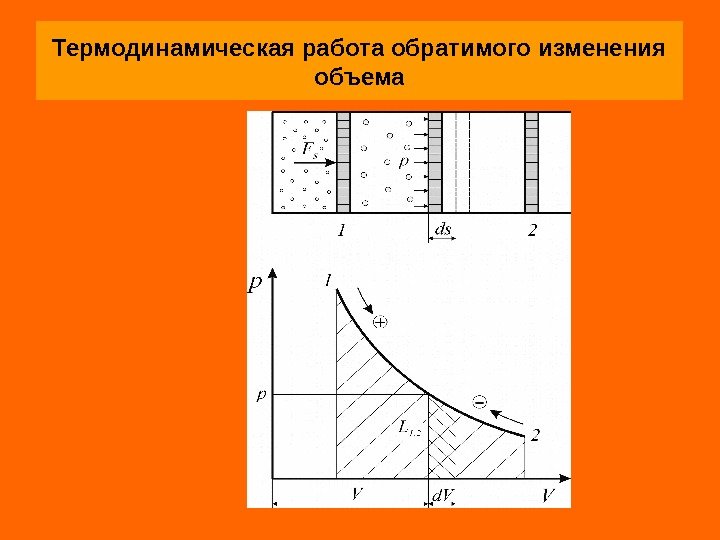
 Термодинамическая работа В простейшем случае элементарная термодинамическая работа L (Дж) простых тел определяется в зависимости от величины давления и изменения объема Удельная элементарная термодинамическая работа обратимого изменения объема (Дж/кг) определяется соотношением ldvp G d. Vp G L l d. Vpdsfpds. FL s
Термодинамическая работа В простейшем случае элементарная термодинамическая работа L (Дж) простых тел определяется в зависимости от величины давления и изменения объема Удельная элементарная термодинамическая работа обратимого изменения объема (Дж/кг) определяется соотношением ldvp G d. Vp G L l d. Vpdsfpds. FL s
 Термодинамическая работа обратимого изменения объема
Термодинамическая работа обратимого изменения объема
 Поскольку термодинамическая работа зависит от пути (вида) процесса, для вычисления интегральных значений полной ( ) , или удельной ( ) работы должны быть заданы уравнения процессов изменения состояния тела в форме , либо его графиче-ское изображение в диаграммах состояния р – V или р – v. Как следует из рисунка термодинамическая работа определяется площадью под кривой процесса независимо от вида рабочего тела и его свойств. В силу этого координаты р–V и р– v называются универсальными координатами работы. Работа расширения считается положительной ( , ), а работа сжатия – отрицательной ( ). 2, 1 L 2, 1 l 0)V, p( 0 dv 0 l 0 l, 0 dv
Поскольку термодинамическая работа зависит от пути (вида) процесса, для вычисления интегральных значений полной ( ) , или удельной ( ) работы должны быть заданы уравнения процессов изменения состояния тела в форме , либо его графиче-ское изображение в диаграммах состояния р – V или р – v. Как следует из рисунка термодинамическая работа определяется площадью под кривой процесса независимо от вида рабочего тела и его свойств. В силу этого координаты р–V и р– v называются универсальными координатами работы. Работа расширения считается положительной ( , ), а работа сжатия – отрицательной ( ). 2, 1 L 2, 1 l 0)V, p( 0 dv 0 l 0 l, 0 dv
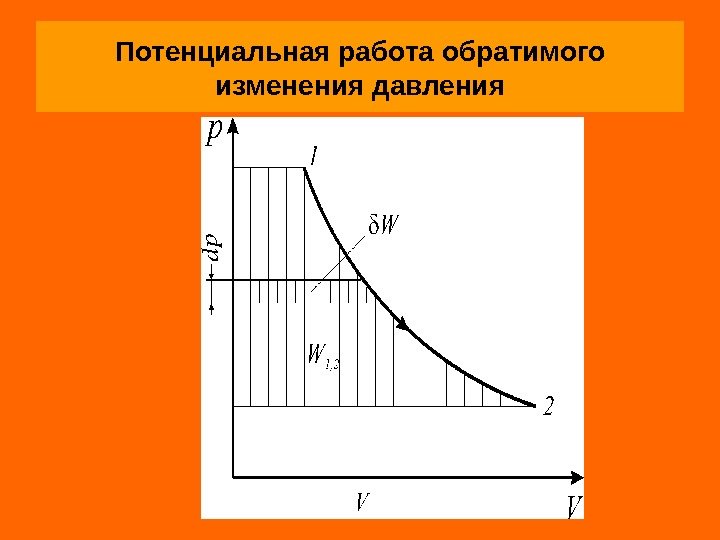
 Потенциальная (техническая) работа Потенциальной (технической) работой называется работа по перемещению сплошных масс (газа, пара или жидкости) из области одного давления ( p 1 ) в область другого давления ( p 2 ), т. е. потенциальная работа — это работа обратимого изменения давления. Элементарная потенциальная работа простого тела определяется из соотношения Удельная потенциальная работа в элементарном процессе определяется по формуле Vdp. W vdp G W w
Потенциальная (техническая) работа Потенциальной (технической) работой называется работа по перемещению сплошных масс (газа, пара или жидкости) из области одного давления ( p 1 ) в область другого давления ( p 2 ), т. е. потенциальная работа — это работа обратимого изменения давления. Элементарная потенциальная работа простого тела определяется из соотношения Удельная потенциальная работа в элементарном процессе определяется по формуле Vdp. W vdp G W w
 Потенциальная работа обратимого изменения давления
Потенциальная работа обратимого изменения давления
 Для определения интегральных значений полной ( ) или удельной ( ) работы надо знать уравнение процесса изменения состояния рабочего тела или его графическое изображение в диаграммах состояния р – V или р – v. Как и в случае термодинамической работы, потен-циальная работа определяется в кооординатах р – V площадью между кривой процесса и осью абсцисс независимо от вида рабочего тела и его свойств. Термодинамическая и потенциальная работы в обратимом процессе есть сумма эффективной работы и необратимых потерь работы 2, 1 W 2, 1 w , LLL WWW
Для определения интегральных значений полной ( ) или удельной ( ) работы надо знать уравнение процесса изменения состояния рабочего тела или его графическое изображение в диаграммах состояния р – V или р – v. Как и в случае термодинамической работы, потен-циальная работа определяется в кооординатах р – V площадью между кривой процесса и осью абсцисс независимо от вида рабочего тела и его свойств. Термодинамическая и потенциальная работы в обратимом процессе есть сумма эффективной работы и необратимых потерь работы 2, 1 W 2, 1 w , LLL WWW
 Необратимые потери термодинамической ( ) и потенциальной ( ) работ превращаются в теплоту внутреннего теплообмена ( ). Эффективная термодинамическая работа ( ) простого тела в замкнутом пространстве и эффектив-ная потенциальная работа ( ) потока непосредст-венно передаются внешней системе ( ) и ( или ) используются для изменения энергии внешнего положения тела ( d. Ecz ). = + d. E cz ; = + d. Ecz Q L ** W * L * W * cz. W * L * cz. L * W * cz. W
Необратимые потери термодинамической ( ) и потенциальной ( ) работ превращаются в теплоту внутреннего теплообмена ( ). Эффективная термодинамическая работа ( ) простого тела в замкнутом пространстве и эффектив-ная потенциальная работа ( ) потока непосредст-венно передаются внешней системе ( ) и ( или ) используются для изменения энергии внешнего положения тела ( d. Ecz ). = + d. E cz ; = + d. Ecz Q L ** W * L * W * cz. W * L * cz. L * W * cz. W
 Внутренняя энергия тела Внутренняя энергия представляет собой полный запас энергии тела и состоит из энергии поступатель-ного и вращательного движения молекул, энергии внутримолекулярных колебаний, потенциальной энергии сил сцепления между молекулами, внутримолекулярной энергии, внутриато-мной энергии. Внутренняя энергия U является функцией состояния, она не зависит от пути процесса, а ее элементарное изменение обозначается символом полного дифференциала ( d U). Внутренняя энергия измеряется в Джоулях ( Дж ), а удельная внутренняя энергия ( u ) — в Дж/кг. Для простых тел внутренняя энергия определяется как функция двух переменных ( р, T ; р, v или T , v ).
Внутренняя энергия тела Внутренняя энергия представляет собой полный запас энергии тела и состоит из энергии поступатель-ного и вращательного движения молекул, энергии внутримолекулярных колебаний, потенциальной энергии сил сцепления между молекулами, внутримолекулярной энергии, внутриато-мной энергии. Внутренняя энергия U является функцией состояния, она не зависит от пути процесса, а ее элементарное изменение обозначается символом полного дифференциала ( d U). Внутренняя энергия измеряется в Джоулях ( Дж ), а удельная внутренняя энергия ( u ) — в Дж/кг. Для простых тел внутренняя энергия определяется как функция двух переменных ( р, T ; р, v или T , v ).
 Теплота — количество энергии, передаваемой от одного тела к другому посредством теплопро-водности, конвективного или лучистого тепло-обмена. Процесс передачи теплоты называется теплообменом. Количество теплоты , получаемое телом в результате теплообмена, зависит от вида термо-динамического процесса и аналогично работе является функцией процесса. Поэтому, элементар-ное количество теплоты не является полным дифференциалом ( ). Количество теплоты измеряется в Джоулях ( Дж ), а удельное количество теплоты = / в Дж/кг. QQ q Qq. G
Теплота — количество энергии, передаваемой от одного тела к другому посредством теплопро-водности, конвективного или лучистого тепло-обмена. Процесс передачи теплоты называется теплообменом. Количество теплоты , получаемое телом в результате теплообмена, зависит от вида термо-динамического процесса и аналогично работе является функцией процесса. Поэтому, элементар-ное количество теплоты не является полным дифференциалом ( ). Количество теплоты измеряется в Джоулях ( Дж ), а удельное количество теплоты = / в Дж/кг. QQ q Qq. G
 Теплоемкость Истиной теплоемкостью называется количество теплоты, которое надо сообщить единице количества вещества в термодинамическом процессе ( z=idem. ) , чтобы его температура повысилась на 1 градус. Различают массовую теплоемкость с , измеряемую в Дж/ (кг К) , молярную – Дж/(кмоль К) и объемную с’ – Дж/(м 3 К). dt q c z z c
Теплоемкость Истиной теплоемкостью называется количество теплоты, которое надо сообщить единице количества вещества в термодинамическом процессе ( z=idem. ) , чтобы его температура повысилась на 1 градус. Различают массовую теплоемкость с , измеряемую в Дж/ (кг К) , молярную – Дж/(кмоль К) и объемную с’ – Дж/(м 3 К). dt q c z z c
 Связь между массовой, молярной и объемной теплоемкостью представлена следующими соотношениями: Экспериментальное определение теплоемкости обычно проводится в двух процессах: при постоянном объеме z=v=idem. (изохорная теплоемкость cv ) и постоянном давлении z=p=idem. (изобарная теплоемкость c p ). cc cc
Связь между массовой, молярной и объемной теплоемкостью представлена следующими соотношениями: Экспериментальное определение теплоемкости обычно проводится в двух процессах: при постоянном объеме z=v=idem. (изохорная теплоемкость cv ) и постоянном давлении z=p=idem. (изобарная теплоемкость c p ). cc cc
 Теплоемкость реального газа зависит от температуры и давления. Теплоемкость идеального газа зависит только от температуры. Для практических расчетов вводится понятие средней теплоемкости в интервале температур от t 1 до t 2 , значение которой принимается неизменной для всего рассматриваемого интервала температур ( с zm ). Из выражения истинной теплоемкости следует, что количество теплоты, подведенной к телу (или отведен-ной от него) в изобарном или изохорном процессе 1 -2, определяется соотношением Отсюда следует выражение средней теплоемкости газа 2 1 12 zmz )tt(cdtcq 2,
Теплоемкость реального газа зависит от температуры и давления. Теплоемкость идеального газа зависит только от температуры. Для практических расчетов вводится понятие средней теплоемкости в интервале температур от t 1 до t 2 , значение которой принимается неизменной для всего рассматриваемого интервала температур ( с zm ). Из выражения истинной теплоемкости следует, что количество теплоты, подведенной к телу (или отведен-ной от него) в изобарном или изохорном процессе 1 -2, определяется соотношением Отсюда следует выражение средней теплоемкости газа 2 1 12 zmz )tt(cdtcq 2,
 Для некоторых газов в определенном интервале температур истинная теплоемкость изменяется по линейному закону тогда сzm — первая средняя теплоемкость. Она численно равна истинной теплоемкости при среднеарифметической температуре процесса. tbac zzz dtc tt 1 tt q c 2 1 z 1212 2, 1 zm 2 )tt( ba )tt( dt)tba( c 21 zz 12 2 1 zz zm
Для некоторых газов в определенном интервале температур истинная теплоемкость изменяется по линейному закону тогда сzm — первая средняя теплоемкость. Она численно равна истинной теплоемкости при среднеарифметической температуре процесса. tbac zzz dtc tt 1 tt q c 2 1 z 1212 2, 1 zm 2 )tt( ba )tt( dt)tba( c 21 zz 12 2 1 zz zm
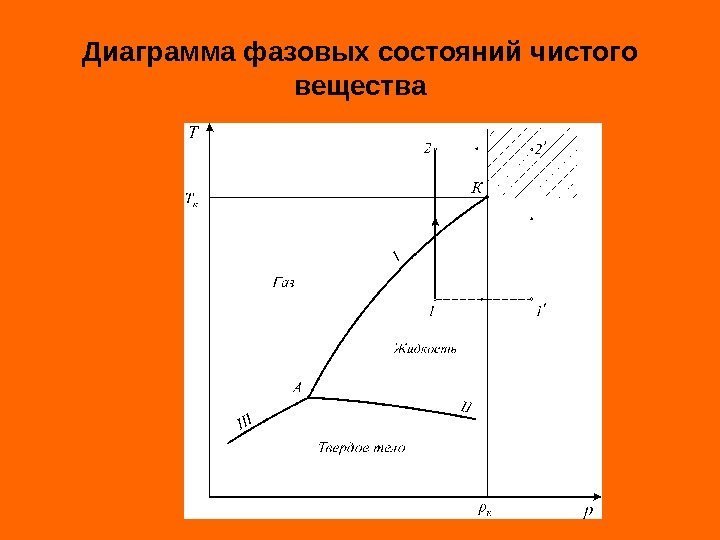
 Различают три агрегатных состояния простых систем: твердое, жидкое и газовое. Линии фазовых превращений (испарение — I , плавление — II , сублимации — III ) отображают термодинамическое равновесие двухфазных систем и делят диаграмму на области различных агрегатных состояний. Энергетической границей между жидкостью и паром является теплота испарения , а между твердым телом и жидкостью – теплота плавления. Так как процессы испарения и плавления протекают при постоянной температуре, то теплоты испарения, плавления и сублимации есть теплоты изотермических превращений. Теплота фазового перехода обозначается символом r.
Различают три агрегатных состояния простых систем: твердое, жидкое и газовое. Линии фазовых превращений (испарение — I , плавление — II , сублимации — III ) отображают термодинамическое равновесие двухфазных систем и делят диаграмму на области различных агрегатных состояний. Энергетической границей между жидкостью и паром является теплота испарения , а между твердым телом и жидкостью – теплота плавления. Так как процессы испарения и плавления протекают при постоянной температуре, то теплоты испарения, плавления и сублимации есть теплоты изотермических превращений. Теплота фазового перехода обозначается символом r.
 Диаграмма фазовых состояний чистого вещества
Диаграмма фазовых состояний чистого вещества
 Критические параметры являются важнейшими термодинамическими постоянными вещества. Критическая температура – это температура, при которой и выше которой газ никаким сжатием не может быть переведен в жидкое состояние. Критическое давление – это такое давление, при котором и выше которого жидкость невозможно перевести в газообразное состояние никаким изменением температуры. В закритической области ( ) вещество может находиться только в однофазном состоянии. Переход из состояния 1 в состояние 2 возможен кратчайшим путем по линии 1 -2. Можно этот переход осуществить через закритическую область, то есть без изменения агрегатного состояния, например по линиикк. TT; pp
Критические параметры являются важнейшими термодинамическими постоянными вещества. Критическая температура – это температура, при которой и выше которой газ никаким сжатием не может быть переведен в жидкое состояние. Критическое давление – это такое давление, при котором и выше которого жидкость невозможно перевести в газообразное состояние никаким изменением температуры. В закритической области ( ) вещество может находиться только в однофазном состоянии. Переход из состояния 1 в состояние 2 возможен кратчайшим путем по линии 1 -2. Можно этот переход осуществить через закритическую область, то есть без изменения агрегатного состояния, например по линиикк. TT; pp
 Поэтому в принципе, для простых тел (однородных систем) должно существовать единое уравнение состояния , описывающее любое одно-фазное состояние вещества. Уравнение состояния идеальных газов — уравнение Клапейрона : для 1 кг газа для G кг газа для 1 кмоля газа для кмолей газа 0)T, v, p(F RTpv GRTp. V G TRvp TRGp. V
Поэтому в принципе, для простых тел (однородных систем) должно существовать единое уравнение состояния , описывающее любое одно-фазное состояние вещества. Уравнение состояния идеальных газов — уравнение Клапейрона : для 1 кг газа для G кг газа для 1 кмоля газа для кмолей газа 0)T, v, p(F RTpv GRTp. V G TRvp TRGp. V
 где R – характеристическая постоянная газа; Т – абсолютная температура газа ; ( Дж/кмоль К ) – универсальная газовая постоянная, не зависящей от природы газов. В инженерных расчетах часто пользуются уравнением состояния идеального газа с введением в него поправочного коэффициента ( z ), называемого коэффициентом сжимаемости Коэффициент сжимаемости ( z ) учитывает различие между идеальным и реальными газами (для идеаль — ного газа z = 1 ). 8314 RR z. RTpv
где R – характеристическая постоянная газа; Т – абсолютная температура газа ; ( Дж/кмоль К ) – универсальная газовая постоянная, не зависящей от природы газов. В инженерных расчетах часто пользуются уравнением состояния идеального газа с введением в него поправочного коэффициента ( z ), называемого коэффициентом сжимаемости Коэффициент сжимаемости ( z ) учитывает различие между идеальным и реальными газами (для идеаль — ного газа z = 1 ). 8314 RR z. RTpv
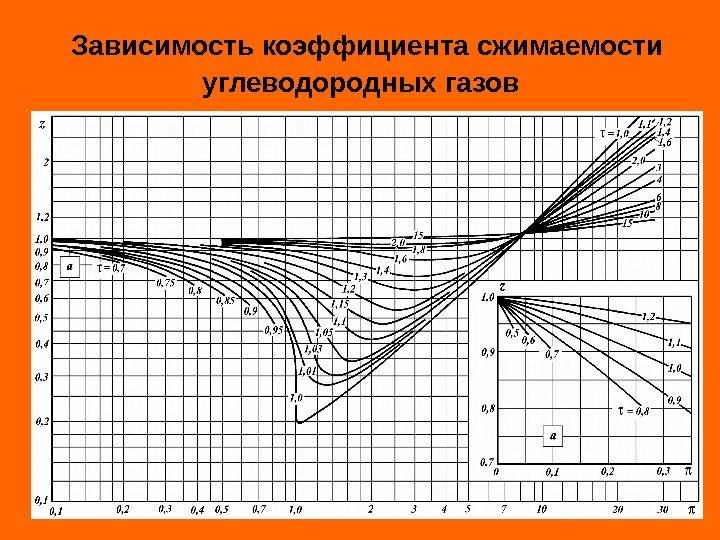
 Для обобщения данных по коэффициентам сжимаемости различных газов был использован прин — цип «соответственных» состояний, сформулирован — ный Ван-дер-Ваальсом. Принцип «соответственных» состояний утверждает, что критическое состояние действительно является одинаковым для всех веществ. В критической точке для всех веществ r = 0, . Вещества находятся в соответственных состояниях при одинаковом удалении от критической точки. 0 T p v 2 2 0 v p v 0 v p T
Для обобщения данных по коэффициентам сжимаемости различных газов был использован прин — цип «соответственных» состояний, сформулирован — ный Ван-дер-Ваальсом. Принцип «соответственных» состояний утверждает, что критическое состояние действительно является одинаковым для всех веществ. В критической точке для всех веществ r = 0, . Вещества находятся в соответственных состояниях при одинаковом удалении от критической точки. 0 T p v 2 2 0 v p v 0 v p T
 Степень удаления от критической точки определяется с помощью приведенных параметров: приведенного давления приведенной температуры приведенного объема кp p к. T T к v v w
Степень удаления от критической точки определяется с помощью приведенных параметров: приведенного давления приведенной температуры приведенного объема кp p к. T T к v v w
 Зависимость коэффициента сжимаемости углеводородных газов
Зависимость коэффициента сжимаемости углеводородных газов
 Смеси жидкостей, паров и газов Смесью называется термодинамическая система состоящая из n -компонентов химический не взаимодействующих между собой веществ. Массовой концентрацией или массовой долей mi называется отношение массы компонента к массе всей смеси n 1 i i ii G G m
Смеси жидкостей, паров и газов Смесью называется термодинамическая система состоящая из n -компонентов химический не взаимодействующих между собой веществ. Массовой концентрацией или массовой долей mi называется отношение массы компонента к массе всей смеси n 1 i i ii G G m
 Молярной концентрацией или молярной долей i -го компонента называется отношение количества киломолей этого компонента к общему числу киломолей смеси ir i. G n 1 i i ii i G G r
Молярной концентрацией или молярной долей i -го компонента называется отношение количества киломолей этого компонента к общему числу киломолей смеси ir i. G n 1 i i ii i G G r
 Средняя (кажущаяся) молярная масса смеси равна отношению массы смеси к количеству киломолей смеси и может быть определена из следующих соотношений: = = = = G G m G G n 1 i ii G G n 1 i ii r G G n 1 i ii. G G 1 n 1 ii im
Средняя (кажущаяся) молярная масса смеси равна отношению массы смеси к количеству киломолей смеси и может быть определена из следующих соотношений: = = = = G G m G G n 1 i ii G G n 1 i ii r G G n 1 i ii. G G 1 n 1 ii im
 Зависимость между массовой и молярной концентрациями устанавливается соотношением Газовая постоянная смеси может быть вычислена по следующему выражению: =m i i i r m R R m n 1 ii i R r 1 n 1 i ii r R Rm
Зависимость между массовой и молярной концентрациями устанавливается соотношением Газовая постоянная смеси может быть вычислена по следующему выражению: =m i i i r m R R m n 1 ii i R r 1 n 1 i ii r R Rm
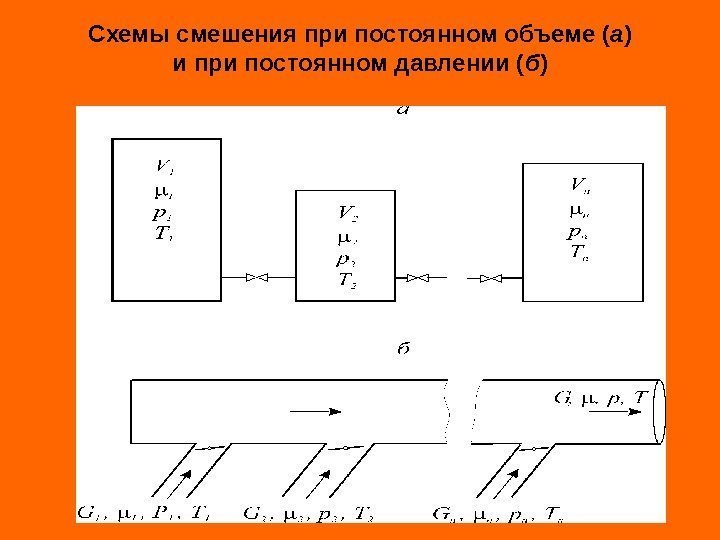
 Схемы смешения при постоянном объеме ( а ) и при постоянном давлении ( б )
Схемы смешения при постоянном объеме ( а ) и при постоянном давлении ( б )
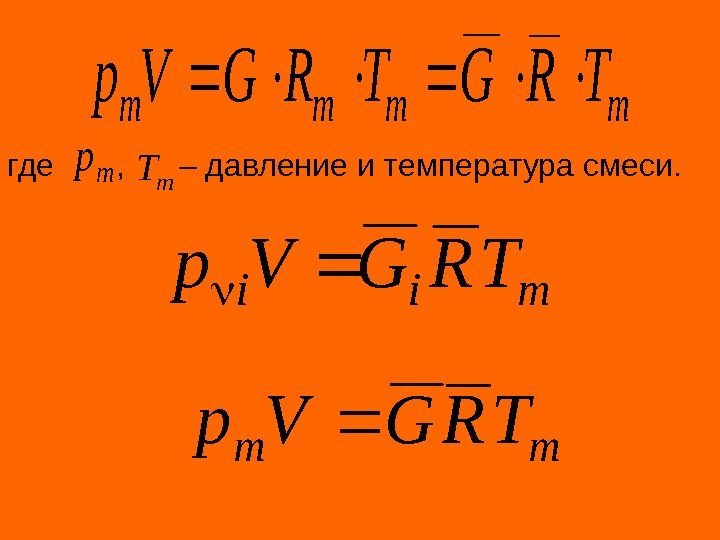 где , – давление и температура смеси. mmmm TRGTRGVp m p m. T mii TRGVp mm TRGVp
где , – давление и температура смеси. mmmm TRGTRGVp m p m. T mii TRGVp mm TRGVp
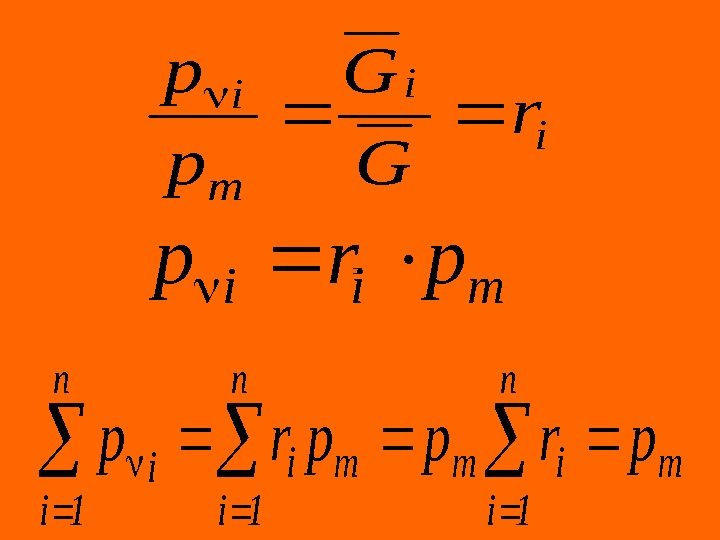 i i m i r G G p p mii prp = = m n 1 i im n 1 i mii prpprp
i i m i r G G p p mii prp = = m n 1 i im n 1 i mii prpprp
 где массовая и молярная концентрации i — го компо-нента смеси; — средние удельные массовая и молярная теплоемкости i — го компонента смеси в процессах ( ); — средние удельные массовая и молярная теплоемкости смеси, ii, zm n 1 i i zm m. Tcm c 1 Tcr с 1 T iir, m i, zmc, с idemzv, pzzmzmc, с n 1 i i, zmizm cmc n 1 i i, zmizm crc
где массовая и молярная концентрации i — го компо-нента смеси; — средние удельные массовая и молярная теплоемкости i — го компонента смеси в процессах ( ); — средние удельные массовая и молярная теплоемкости смеси, ii, zm n 1 i i zm m. Tcm c 1 Tcr с 1 T iir, m i, zmc, с idemzv, pzzmzmc, с n 1 i i, zmizm cmc n 1 i i, zmizm crc
 Смеси реальных газов , pк, i и Тк, i критические давление и температура компонентов газовой смеси. mmmm TRGz. Vp n 1 i i, кiпк prp n 1 i i, кiпк Tr. T
Смеси реальных газов , pк, i и Тк, i критические давление и температура компонентов газовой смеси. mmmm TRGz. Vp n 1 i i, кiпк prp n 1 i i, кiпк Tr. T
 Первое начало термодинамики – это количественное выражение закона сохранения и превращения энергии. Закон сохранения и превращения энергии является универсальным законом природы и применим ко всем явлениям. Он гласит: «запас энергии изолированной системы остается неизменным при любых происходящих в системе процессах; энергия не уничтожается и не создается, а только переходит из одного вида в другой» . Это утверждение и принимается в качестве пастулата первого начала термодинамики
Первое начало термодинамики – это количественное выражение закона сохранения и превращения энергии. Закон сохранения и превращения энергии является универсальным законом природы и применим ко всем явлениям. Он гласит: «запас энергии изолированной системы остается неизменным при любых происходящих в системе процессах; энергия не уничтожается и не создается, а только переходит из одного вида в другой» . Это утверждение и принимается в качестве пастулата первого начала термодинамики
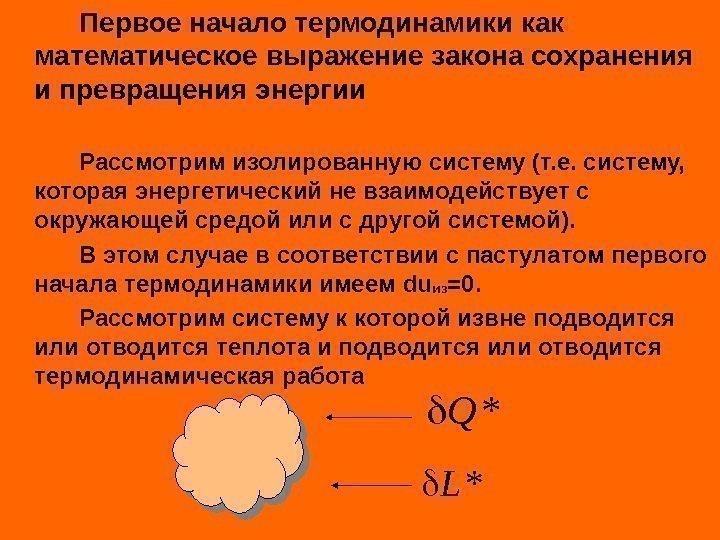
 Первое начало термодинамики как математическое выражение закона сохранения и превращения энергии Рассмотрим изолированную систему (т. е. систему, которая энергетический не взаимодействует с окружающей средой или с другой системой). В этом случае в соответствии с пастулатом первого начала термодинамики имеем duиз =0. Рассмотрим систему к которой извне подводится или отводится теплота и подводится или отводится термодинамическая работа *L *Q
Первое начало термодинамики как математическое выражение закона сохранения и превращения энергии Рассмотрим изолированную систему (т. е. систему, которая энергетический не взаимодействует с окружающей средой или с другой системой). В этом случае в соответствии с пастулатом первого начала термодинамики имеем duиз =0. Рассмотрим систему к которой извне подводится или отводится теплота и подводится или отводится термодинамическая работа *L *Q
 Таким образом изменение внутренней энергии системы равно алгебраической сумме подведенных извне теплоты и термодинамической работы (подведенная теплота — положительна, подведенная работа — отрицательна ) в интегральной форме 2, 1 * 122, 1 LUUQ *LQd. U Ld. UQ * или
Таким образом изменение внутренней энергии системы равно алгебраической сумме подведенных извне теплоты и термодинамической работы (подведенная теплота — положительна, подведенная работа — отрицательна ) в интегральной форме 2, 1 * 122, 1 LUUQ *LQd. U Ld. UQ * или
 — эффективная работа; — внешний теплообмен Полученные уравнения учитывают только внешние эффекты и справедливы только для обратимых процессов. Уравнения являются математическим выраже- нием первого начала термодинамики по внешнему балансу теплоты и работы и гласят: количество теплоты подведенное извне идет на изменение внутренней энергии системы и совершение работы. Принимая во внимание, что эффективная работа связана с термодинамической работой соотношение и*L *Q **LL*L**Q**L
— эффективная работа; — внешний теплообмен Полученные уравнения учитывают только внешние эффекты и справедливы только для обратимых процессов. Уравнения являются математическим выраже- нием первого начала термодинамики по внешнему балансу теплоты и работы и гласят: количество теплоты подведенное извне идет на изменение внутренней энергии системы и совершение работы. Принимая во внимание, что эффективная работа связана с термодинамической работой соотношение и*L *Q **LL*L**Q**L
 *; *LQ ** **Q*QQ Ld. UQQQ 2, 112 ** 2, 1 LUUQQQ уравнения первого начала термодинамики по балансу рабочего тела , и справедливы для реальных процессов. В обратимых процессах и уравнения первого начала термодинамики по внешнему балансу и балансу рабочего тела совпадают имеем 0**QL **
*; *LQ ** **Q*QQ Ld. UQQQ 2, 112 ** 2, 1 LUUQQQ уравнения первого начала термодинамики по балансу рабочего тела , и справедливы для реальных процессов. В обратимых процессах и уравнения первого начала термодинамики по внешнему балансу и балансу рабочего тела совпадают имеем 0**QL **
 Первое начало термодинамики для простых тел Для простых тел, то есть систем, состояние которых определяется двумя независимыми перемен-ными, термодинамическая работа определяется как и математическое выражение первого начала термодинамики в дифференциальной форме примет следующий вид: для термодинамической системы для 1 кг системыpd. Vd. ULd. UQ pdvdulduq d. Vp. L
Первое начало термодинамики для простых тел Для простых тел, то есть систем, состояние которых определяется двумя независимыми перемен-ными, термодинамическая работа определяется как и математическое выражение первого начала термодинамики в дифференциальной форме примет следующий вид: для термодинамической системы для 1 кг системыpd. Vd. ULd. UQ pdvdulduq d. Vp. L
 Выражение удельной потенциальной работы можно представить в виде соотношения из которого следует, что ; и , Сумма удельной внутренней энергии ( ) и потенциальной функции ( ) называется удельной энтальпией ( ) (Дж/кг). )pv(dpdvpdvpdvvdpw )pv(dlw)pv(dwl )pv(dwduqw)pvu(dq u pv pvuh
Выражение удельной потенциальной работы можно представить в виде соотношения из которого следует, что ; и , Сумма удельной внутренней энергии ( ) и потенциальной функции ( ) называется удельной энтальпией ( ) (Дж/кг). )pv(dpdvpdvpdvvdpw )pv(dlw)pv(dwl )pv(dwduqw)pvu(dq u pv pvuh
 Первое начало термодинамики для 1 кг простого тела по балансу рабочего тела в дифференциальной и интегральной форме: vdpdhpdvduq 2 1 122, 1 vdphhdvpuuq Первое начало термодинамики по внешнему балансу 2 1122, 1 vdphhdvpuu*q vdpdhpdvduq *
Первое начало термодинамики для 1 кг простого тела по балансу рабочего тела в дифференциальной и интегральной форме: vdpdhpdvduq 2 1 122, 1 vdphhdvpuuq Первое начало термодинамики по внешнему балансу 2 1122, 1 vdphhdvpuu*q vdpdhpdvduq *
 Аналитическое выражение первого начала термодинамики Значения удельных внутренней энергии и энтальпии простого тела однозначно определяются двумя независимыми переменными и могут быть представлены следующим образом: Изменения внутренней энергии и энтальпии простого тела, как функций состояния, в элементарных процессах являются полными дифференциалами и определяются соотношениями); v, T(fu)p, T(fh dv v u d. Tcdv v u d. T T u du T v Tv
Аналитическое выражение первого начала термодинамики Значения удельных внутренней энергии и энтальпии простого тела однозначно определяются двумя независимыми переменными и могут быть представлены следующим образом: Изменения внутренней энергии и энтальпии простого тела, как функций состояния, в элементарных процессах являются полными дифференциалами и определяются соотношениями); v, T(fu)p, T(fh dv v u d. Tcdv v u d. T T u du T v Tv
 Подставляя выражения полных дифференциалов внутренней энергии и энтальпии в уравнение первого начала термодинамики имеемdp p h d. Tcdv p h d. T T h dh T p Tp dpv dp dh d. Tcdvp v u d. Tcq T p T v vdpdhpdvduq
Подставляя выражения полных дифференциалов внутренней энергии и энтальпии в уравнение первого начала термодинамики имеемdp p h d. Tcdv p h d. T T h dh T p Tp dpv dp dh d. Tcdvp v u d. Tcq T p T v vdpdhpdvduq
 Данное соотношение называется первым началом термодинамики для простых тел в аналитической форме. Выражения в квадратных скобках в литературе часто называют калорическими коэффициентами, которые могут быть определены по формулам, полученным с использованием дифференциальных соотношений термодинамики , uv T v Dcpp v u h )Dcv(v dp dh hhp T p
Данное соотношение называется первым началом термодинамики для простых тел в аналитической форме. Выражения в квадратных скобках в литературе часто называют калорическими коэффициентами, которые могут быть определены по формулам, полученным с использованием дифференциальных соотношений термодинамики , uv T v Dcpp v u h )Dcv(v dp dh hhp T p
 – коэффициент Джоуля – Гей Люссака , – коэффициент Джоуля-Томсона, Коэффициенты Джоуля – Гей Люссака ( ) и Джоуля-Томсона ( ) реальных газов определяются по таблицам термодинамических свойств. u D u u v T D h h p T D h. D u. D h.
– коэффициент Джоуля – Гей Люссака , – коэффициент Джоуля-Томсона, Коэффициенты Джоуля – Гей Люссака ( ) и Джоуля-Томсона ( ) реальных газов определяются по таблицам термодинамических свойств. u D u u v T D h h p T D h. D u. D h.
 Калорические коэффициенты по физическому смыслу являются аналогами теплоемкостей в изотермическом процессе. Данную запись первого начала называют аналити-ческим выражением первого начала термодинамики для простого тела. Первое начало термодинамики для идеальных газов. Закон Майера. Энтропия идеального газа Идеальные газы подчиняются уравнению состояния Клапейрона и закону Джоуля, согласно которому удельная внутренняя энергия идеального газа зависит только от температуры dphd. Tcdvhd. Tcq ppvv RTpv
Калорические коэффициенты по физическому смыслу являются аналогами теплоемкостей в изотермическом процессе. Данную запись первого начала называют аналити-ческим выражением первого начала термодинамики для простого тела. Первое начало термодинамики для идеальных газов. Закон Майера. Энтропия идеального газа Идеальные газы подчиняются уравнению состояния Клапейрона и закону Джоуля, согласно которому удельная внутренняя энергия идеального газа зависит только от температуры dphd. Tcdvhd. Tcq ppvv RTpv
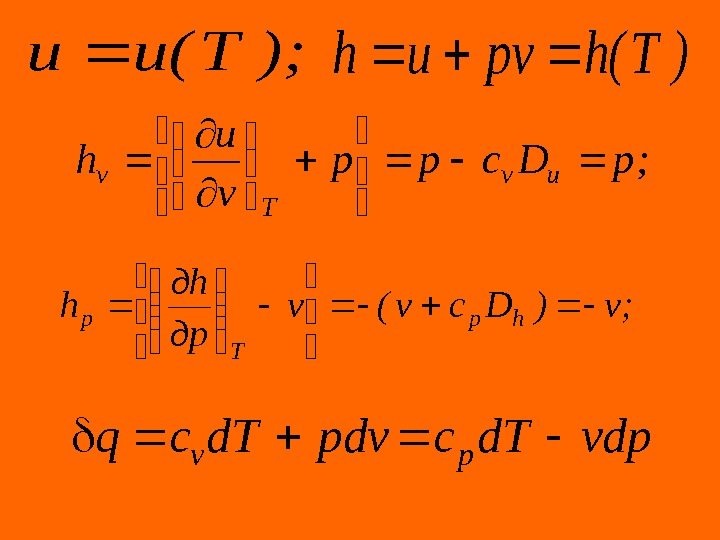 ; p. Dcpp vu h uv Tv ; v)Dcv(v дp дh hhp T p ); T(uu)T(hpvuh vdpd. Tcpdvd. Tcq pv
; p. Dcpp vu h uv Tv ; v)Dcv(v дp дh hhp T p ); T(uu)T(hpvuh vdpd. Tcpdvd. Tcq pv
 С другой стороны из выражения первого начала термодинамики для простого тела С учетом того, что для идеального газа имеем vdpdupdvduq ; d. Tcdv v u d. T T u duv T v Tv d. Tcdp p h d. Tcdv p h d. T T h dhp T p Tp vdpd. Tcpdvd. Tcq pv 2, 112 pm 2, 112 vm 2, 1 w. TTcl. TTcq
С другой стороны из выражения первого начала термодинамики для простого тела С учетом того, что для идеального газа имеем vdpdupdvduq ; d. Tcdv v u d. T T u duv T v Tv d. Tcdp p h d. Tcdv p h d. T T h dhp T p Tp vdpd. Tcpdvd. Tcq pv 2, 112 pm 2, 112 vm 2, 1 w. TTcl. TTcq
 Из уравнения первого начала термодинамики для идеального газа из которого следует, что разность истинных теплоемкостей идеального газа при постоянном давлении и при постоянном объеме равна величине характеристической газовой постоянной можно получить следующее выражение: Это выражение впервые было получено Р. Майером (1842 г. ) и называется законом Майера. Rd. T)pv(dvdppdvd. T)cc( vp Rcc vp
Из уравнения первого начала термодинамики для идеального газа из которого следует, что разность истинных теплоемкостей идеального газа при постоянном давлении и при постоянном объеме равна величине характеристической газовой постоянной можно получить следующее выражение: Это выражение впервые было получено Р. Майером (1842 г. ) и называется законом Майера. Rd. T)pv(dvdppdvd. T)cc( vp Rcc vp
 Уравнение может быть записано и для одного кмоля газа Разделив уравнение первого начала термодинамики на абсолютную температуру T , получим. RR)cc(cc vpvp dp T v T d. T cdv T p T d. T c T q pv
Уравнение может быть записано и для одного кмоля газа Разделив уравнение первого начала термодинамики на абсолютную температуру T , получим. RR)cc(cc vpvp dp T v T d. T cdv T p T d. T c T q pv
 ; v. R T p p R T v С учетом того, что для идеального газа, исходя уравнения Клапейрона, справедливы равенства: получим p dp R T d. T )T(c v dv R T d. T )T(c T q pv
; v. R T p p R T v С учетом того, что для идеального газа, исходя уравнения Клапейрона, справедливы равенства: получим p dp R T d. T )T(c v dv R T d. T )T(c T q pv
 Правая часть уравнения представляет собой сумму полных дифференциалов. Это значит, что и соотношение есть полный дифференциал некоторой функции состояния идеального газа ( s ), называемой удельной энтропией. Изменение удельной энтропии в элементарном процессе представляет собой полный дифференциал и определяется соотношением. Полученное выражение называется принципом существования энтропии идеального газа. T qq T q ds ***
Правая часть уравнения представляет собой сумму полных дифференциалов. Это значит, что и соотношение есть полный дифференциал некоторой функции состояния идеального газа ( s ), называемой удельной энтропией. Изменение удельной энтропии в элементарном процессе представляет собой полный дифференциал и определяется соотношением. Полученное выражение называется принципом существования энтропии идеального газа. T qq T q ds ***
 После интегрирования уравнения получим, что изменение удельной энтропии идеального газа в процессе (1 -2) может быть найдено из соотношения 1 2 mv 12 v v ln. R T T lncss 2 1 1 2 mp p p ln. R T T lnc
После интегрирования уравнения получим, что изменение удельной энтропии идеального газа в процессе (1 -2) может быть найдено из соотношения 1 2 mv 12 v v ln. R T T lncss 2 1 1 2 mp p p ln. R T T lnc
