SHM: Simple Harmonic Motion Simple Harmonic Motion

SHM: Simple Harmonic Motion

Simple Harmonic Motion (SHM) At the end of this lecture you should • Understand what is meant by a differential equation (DE) • Be able to solve the DE for SHM by using a trial solution • Be able to work problems regarding Simple Harmonic Motion

Periodic motion: Simple Harmonic Motion An object undergoes SHM if, when it is moved from its equilibrium position and released, the restoring force is proportional to the displacement of the object from its equilibrium position and is opposite in direction to the displacement ie it obeys xx makx. F where F is the force, x is the displacement and k is a constant – usually called the force constant

Examples of SHM Atoms in a solid vibrate – amplitude depends on temperature. Simple and Compound pendulum. Not every periodic motion is SHM. However most periodic motions approximate to SHM for small displacements. Also assume no friction etc. Mass on end of Horizontal spring or vertical spring

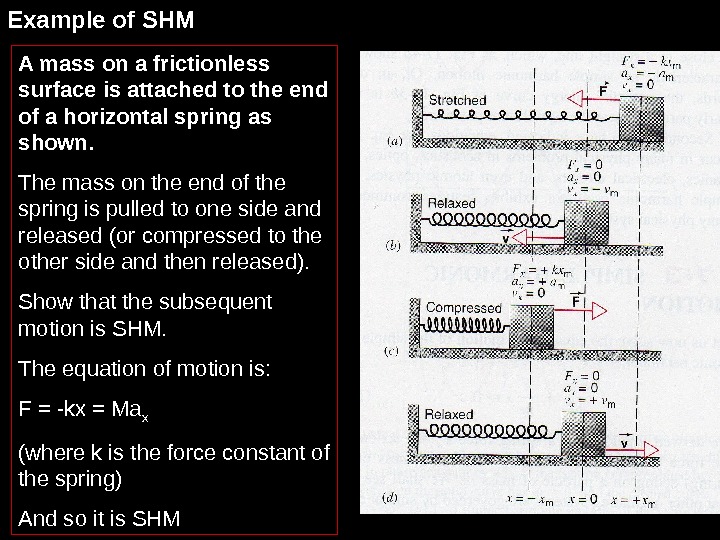
A mass on a frictionless surface is attached to the end of a horizontal spring as shown. The mass on the end of the spring is pulled to one side and released (or compressed to the other side and then released). Show that the subsequent motion is SHM. The equation of motion is: F = -kx = Ma x (where k is the force constant of the spring) And so it is SHMExample of SHM

Example 1 Prove that a mass attached to the end of an ideal vertical spring undergoes SHM when displaced from the equilibrium position.

Simple Pendulum

xmakx. FBasic equation of motion for SHM It is often convenient to write this as: xax 2 where m k 2 This is a differential equation : x dt xd 2 2 2 ( ω is called the angular frequency)

Find displacement x, velocity v, and acceleration a in terms of time Solve the equation: x dt xd 2 2 2 Assume a solution: )sin( t. Ax

Physical meaning of this solution At t = 0 x = 0, so the motion “starts” when the mass is passing through the equilibrium position)sin(t. Ax x varies sinusoidally and the motion repeats with period : 21 Tf and frequency k m T 2 2 ω is called the angular frequency A is called the amplitude and is the maximum displacement. m k 2 The maximum speed is v max = A ω The maximum acceleration is a max = A ω

Compare with xax 2 x m k a x For a spring Then m k 2 Therefore km T 22 For a simple pendulum x L g a x L g 2 Then Therefore g L T

Example 2 A mass of 100 g is on a horizontal spring of force constant k = 10 Nm-1 . It is initially displaced by 0. 1 m, and then released so that it oscillates. Assume friction is negligible. Find: A) the amplitude of the motion B) the period of the motion C) the frequency of the motion

Example 3 An object moving with SHM has an amplitude A = 0. 02 m and a frequency f = 20 Hz. Find: i) period T ii) acceleration at middle and end-points of the motion iii) velocity at middle and end-points iv) The displacement, velocity and acceleration 10 ms after the object passes through the equilibrium position.

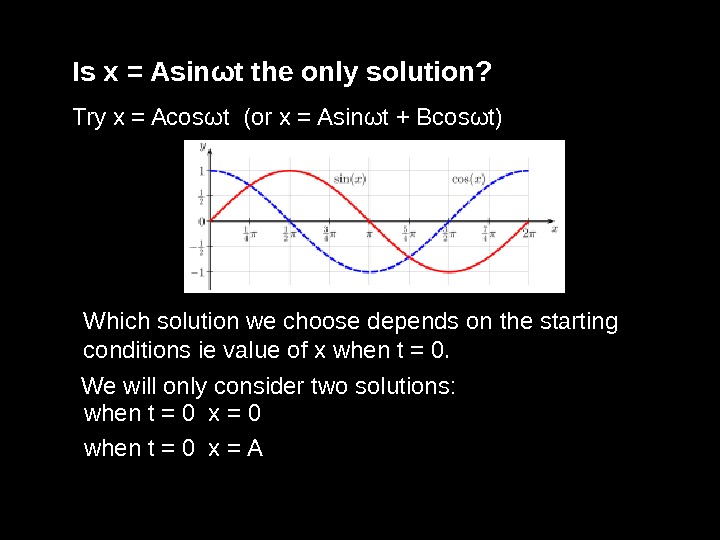
Is x = Asin ω t the only solution? Try x = Acos ω t (or x = Asin ω t + Bcos ω t) Which solution we choose depends on the starting conditions ie value of x when t = 0. We will only consider two solutions: when t = 0 x = 0 when t = 0 x =

Find velocity v and acceleration a in terms of displacement acceleration velocity)cos(t. A dt dx v xa dt xd 2 2 2 )sin( t. Ax 2 v

READING Adams and Allday: 3. 35, 3. 36 At the end of this lecture you should: • Understand what is meant by a differential equation (DE) • Be able to solve the DE for SHM by using a trial solution • Be able to solve problems using the equations of Simple Harmonic Motion