Curs_6_RP_P-invarianti_rus.pptx
- Количество слайдов: 25
 Сети Петри Глава. 6. Фундаментальное уравнение сети Петри. Инварианты. Aurelia Prepelita Conf. , dr. , USM Chisinau, 2010
Сети Петри Глава. 6. Фундаментальное уравнение сети Петри. Инварианты. Aurelia Prepelita Conf. , dr. , USM Chisinau, 2010
 Оглавление: Глава. 6. Фундаментальное уравнение сети Петри. Инварианты. Формы математического представления сетей Петри Допустимая последовательность срабатываний Фундаментальное уравнение сети Петри Графовая Матричная Подстановочная Характеристический вектор последовательности Матрица инциденций Инварианты сети Петри p - инварианты t – инварианты Алгоритм поиска p- инвариантов. Примеры
Оглавление: Глава. 6. Фундаментальное уравнение сети Петри. Инварианты. Формы математического представления сетей Петри Допустимая последовательность срабатываний Фундаментальное уравнение сети Петри Графовая Матричная Подстановочная Характеристический вектор последовательности Матрица инциденций Инварианты сети Петри p - инварианты t – инварианты Алгоритм поиска p- инвариантов. Примеры
 Графовая форма математического представления сетей Петри. Определение: Сетью Петри называется набор из двух множеств (P и T) и двух функций (B и F): PN=
Графовая форма математического представления сетей Петри. Определение: Сетью Петри называется набор из двух множеств (P и T) и двух функций (B и F): PN=
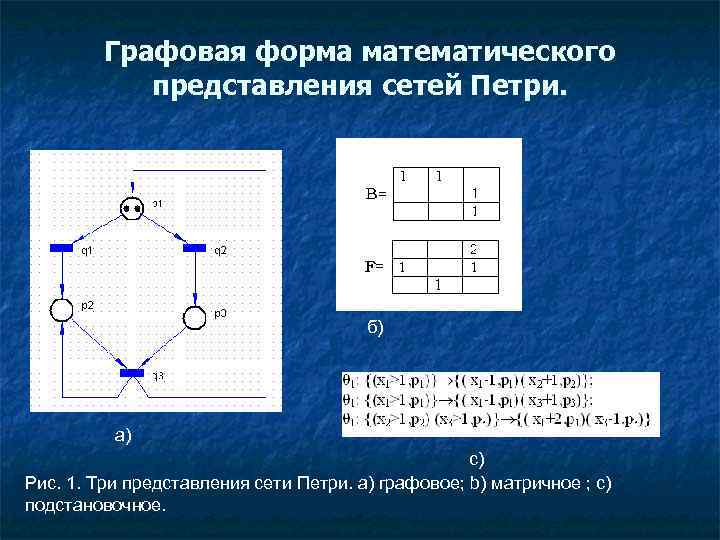 Графовая форма математического представления сетей Петри. б) а) с) Рис. 1. Три представления сети Петри. а) графовое; b) матричное ; с) подстановочное.
Графовая форма математического представления сетей Петри. б) а) с) Рис. 1. Три представления сети Петри. а) графовое; b) матричное ; с) подстановочное.
 Подстановочная форма математического представления сетей Петри Подстановочное представление сети Петри – это множество выражений вида: j: S’j S’’j , j=1, 2, . . . , |T|. (2) Каждая подстановка j выражает входные и выходные условия перехода следующим образом: S’j = {(xi≥bij, pi): pi tj)}; (3) S’’j = {(xi-bij, pi): pi tj) } {(yi+fij, p’i): pi tj )}; (4)
Подстановочная форма математического представления сетей Петри Подстановочное представление сети Петри – это множество выражений вида: j: S’j S’’j , j=1, 2, . . . , |T|. (2) Каждая подстановка j выражает входные и выходные условия перехода следующим образом: S’j = {(xi≥bij, pi): pi tj)}; (3) S’’j = {(xi-bij, pi): pi tj) } {(yi+fij, p’i): pi tj )}; (4)
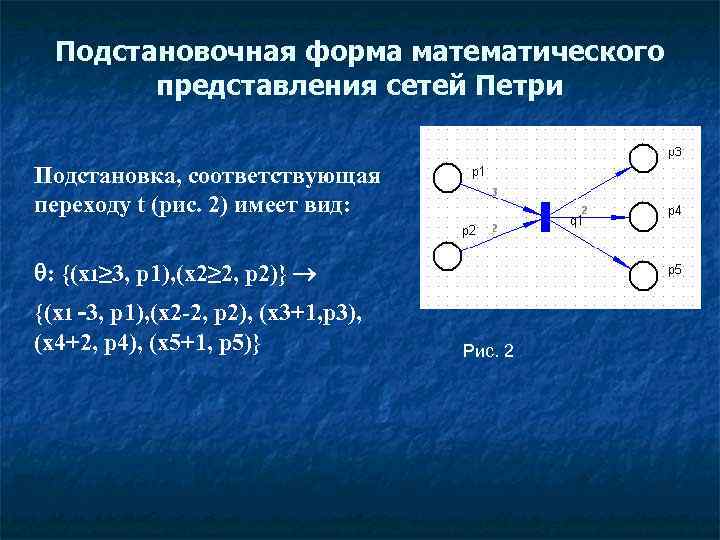 Подстановочная форма математического представления сетей Петри Подстановка, соответствующая переходу t (рис. 2) имеет вид: : {(x 1≥ 3, p 1), (x 2≥ 2, p 2)} {(x 1 -3, p 1), (x 2 -2, p 2), (x 3+1, p 3), (x 4+2, p 4), (x 5+1, p 5)} Рис. 2
Подстановочная форма математического представления сетей Петри Подстановка, соответствующая переходу t (рис. 2) имеет вид: : {(x 1≥ 3, p 1), (x 2≥ 2, p 2)} {(x 1 -3, p 1), (x 2 -2, p 2), (x 3+1, p 3), (x 4+2, p 4), (x 5+1, p 5)} Рис. 2
 Характеристический вектор последовательности Из правил срабатывания переходов следует что достижимые маркировки могут вычисляться путем применения матрично. Векторных операций. Пусть, например, в сети PN=
Характеристический вектор последовательности Из правил срабатывания переходов следует что достижимые маркировки могут вычисляться путем применения матрично. Векторных операций. Пусть, например, в сети PN=
 Матрица инциденций Существует более компактная запись выражения (5): M’=M+C ’, (6) где С=F-B. (7) Выражение (6) можно применять для определения достижимой маркировки М’ , если известна допустимая последовательность срабатываний . Матрица С называется матрицей инциденций сети Петри, а уравнение (6)- фундаментальным уравнением.
Матрица инциденций Существует более компактная запись выражения (5): M’=M+C ’, (6) где С=F-B. (7) Выражение (6) можно применять для определения достижимой маркировки М’ , если известна допустимая последовательность срабатываний . Матрица С называется матрицей инциденций сети Петри, а уравнение (6)- фундаментальным уравнением.
 Фундаментальное уравнение сети Петри играет большую роль в структурной теории сетей Петри. Однако при анализе функционирования сети Петри при заданной маркировке М 0 применять матрицу С следует осторожно, поскольку в общем случае она не является представлением сети Петри – при вычислении сij = fij-bij теряется информация о значениях кратности дуг (pi, tj) и (tj, pi), если обе эти дуги существуют. Иными словами, по матрице С определить матрицу В однозначно невозможно, и, следовательно, невозможно выразить условие возбуждения для перехода tj.
Фундаментальное уравнение сети Петри играет большую роль в структурной теории сетей Петри. Однако при анализе функционирования сети Петри при заданной маркировке М 0 применять матрицу С следует осторожно, поскольку в общем случае она не является представлением сети Петри – при вычислении сij = fij-bij теряется информация о значениях кратности дуг (pi, tj) и (tj, pi), если обе эти дуги существуют. Иными словами, по матрице С определить матрицу В однозначно невозможно, и, следовательно, невозможно выразить условие возбуждения для перехода tj.
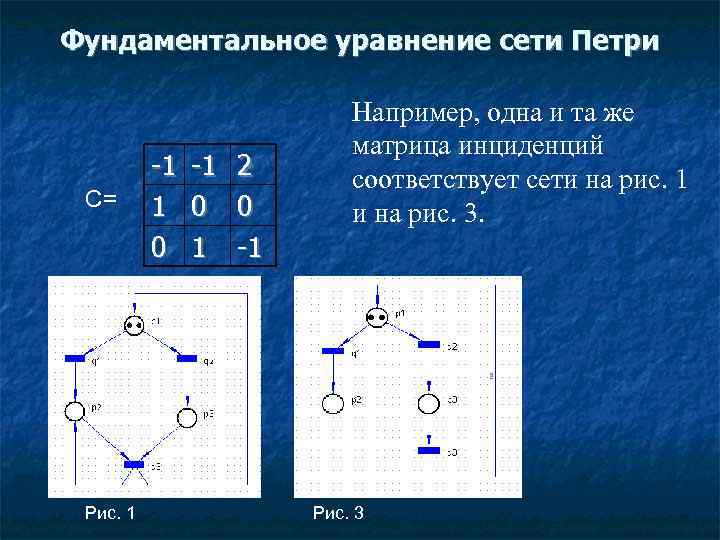 Фундаментальное уравнение сети Петри С= Рис. 1 -1 1 0 -1 0 1 2 0 -1 Например, одна и та же матрица инциденций соответствует сети на рис. 1 и на рис. 3. Рис. 3
Фундаментальное уравнение сети Петри С= Рис. 1 -1 1 0 -1 0 1 2 0 -1 Например, одна и та же матрица инциденций соответствует сети на рис. 1 и на рис. 3. Рис. 3
 Фундаментальное уравнение сети Петри Роль фундаментального уравнения состоит в том, что оно дает формальную возможность исследовать соотношения между последовательностями срабатываний и изменениями маркировок, которые определяются структурными характеристиками сети и не зависят от начальных маркировок: М = M’ – M = C ’. (8) Если М – вектор с неотрицательными компонентами, то M’ ≥ M и согласно условию срабатывания переходов, все переходы, возбужденные при М, возбуждены также при M’.
Фундаментальное уравнение сети Петри Роль фундаментального уравнения состоит в том, что оно дает формальную возможность исследовать соотношения между последовательностями срабатываний и изменениями маркировок, которые определяются структурными характеристиками сети и не зависят от начальных маркировок: М = M’ – M = C ’. (8) Если М – вектор с неотрицательными компонентами, то M’ ≥ M и согласно условию срабатывания переходов, все переходы, возбужденные при М, возбуждены также при M’.
 Фундаментальное уравнение сети Петри Отсюда непосредственно вытекает следующее Утверждение. Все последовательности срабатываний, допустимые в сети
Фундаментальное уравнение сети Петри Отсюда непосредственно вытекает следующее Утверждение. Все последовательности срабатываний, допустимые в сети
 Фундаментальное уравнение сети Петри Например, в сети на рис. 3
Фундаментальное уравнение сети Петри Например, в сети на рис. 3
 Инварианты сети Петри Определение. Повторяющаяся последовательность срабатываний называется стационарно повторяющейся, если она приводит к той же маркировке, из которой началась, т. е. С ’ =0. (9)
Инварианты сети Петри Определение. Повторяющаяся последовательность срабатываний называется стационарно повторяющейся, если она приводит к той же маркировке, из которой началась, т. е. С ’ =0. (9)
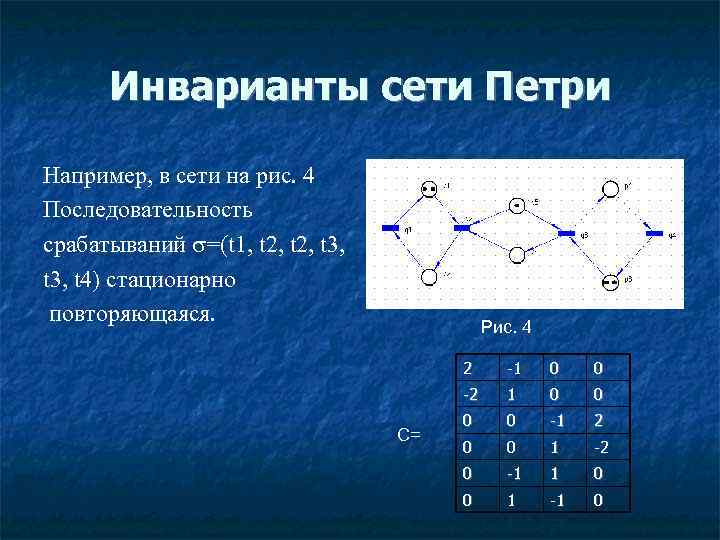 Инварианты сети Петри Например, в сети на рис. 4 Последовательность срабатываний =(t 1, t 2, t 3, t 4) стационарно повторяющаяся. Рис. 4 2 0 0 -2 С= -1 1 0 0 -1 2 0 0 1 -2 0 -1 1 0 0 1 -1 0
Инварианты сети Петри Например, в сети на рис. 4 Последовательность срабатываний =(t 1, t 2, t 3, t 4) стационарно повторяющаяся. Рис. 4 2 0 0 -2 С= -1 1 0 0 -1 2 0 0 1 -2 0 -1 1 0 0 1 -1 0
 t-инварианты сети Петри Определение. t-инвариантом сети Петри N=
t-инварианты сети Петри Определение. t-инвариантом сети Петри N=
 p-инварианты сети Петри Определение. Скалярное произведение положительного целочисленного вектора f=(f 1, . . . , fm), m=|P|, на вектор маркировки f. M= fi M(pi), i=1, . . . , m (11) называется взвешенной суммой маркеров. Вектор f называется весовым, а каждая его компонента fi – весом маркеров в позиции pi.
p-инварианты сети Петри Определение. Скалярное произведение положительного целочисленного вектора f=(f 1, . . . , fm), m=|P|, на вектор маркировки f. M= fi M(pi), i=1, . . . , m (11) называется взвешенной суммой маркеров. Вектор f называется весовым, а каждая его компонента fi – весом маркеров в позиции pi.
 p-инварианты сети Петри Приращение взвешенной суммы маркеров при функционировании сети получается умножением (8) на f М = f * M’ – f *M = f * C ’. Существенно то, что не зависит от М начальной маркировки, т. е. является структурной характеристикой сети.
p-инварианты сети Петри Приращение взвешенной суммы маркеров при функционировании сети получается умножением (8) на f М = f * M’ – f *M = f * C ’. Существенно то, что не зависит от М начальной маркировки, т. е. является структурной характеристикой сети.
 p-инварианты сети Петри Определение. p-инвариантом сети Петри N=
p-инварианты сети Петри Определение. p-инвариантом сети Петри N=
 p-инварианты сети Петри Можно убедиться на примере рис. 4, что f 1=(1, 1, 0, 0), f 2=(0, 0, 1, 1, 0, 0) и f 3=(0, 0, 1, 1)-минимальное порождающее семейство p-инвариантов. Вектор f 4=(1, 1, 1, 1) тоже p-инвариант, но получается как линейная комбинация векторов f 4=f 1+f 2+f 3. Минимальное порождающее семейство t-инвариантов для этой сети содержит только один вектор g=(1, 2, 2, 1).
p-инварианты сети Петри Можно убедиться на примере рис. 4, что f 1=(1, 1, 0, 0), f 2=(0, 0, 1, 1, 0, 0) и f 3=(0, 0, 1, 1)-минимальное порождающее семейство p-инвариантов. Вектор f 4=(1, 1, 1, 1) тоже p-инвариант, но получается как линейная комбинация векторов f 4=f 1+f 2+f 3. Минимальное порождающее семейство t-инвариантов для этой сети содержит только один вектор g=(1, 2, 2, 1).
 Алгоритм поиска p- инвариантов 1. 2. Исходные данные: матрица С размерности mxn. Начальная установка: формируемая матрица B=Emxm. 3. Основной цикл. Выполняется, пока матрица С имеет хотя бы один столбец. Шаг 1: Формируются множества I и J такие, что I={i: ci 1>0}, J={j: cj 1>0}. Шаг 2 : Для каждой пары (i, j) Ix. J выполняется следующее. 2. 1. Приписывается к С строка, равная вектору ci 1*C(j, -) - cj 1*C(i, -) 2. 2. Приписывается к В строка, равная вектору ci 1*B(j, -) - cj 1*B(i, -)
Алгоритм поиска p- инвариантов 1. 2. Исходные данные: матрица С размерности mxn. Начальная установка: формируемая матрица B=Emxm. 3. Основной цикл. Выполняется, пока матрица С имеет хотя бы один столбец. Шаг 1: Формируются множества I и J такие, что I={i: ci 1>0}, J={j: cj 1>0}. Шаг 2 : Для каждой пары (i, j) Ix. J выполняется следующее. 2. 1. Приписывается к С строка, равная вектору ci 1*C(j, -) - cj 1*C(i, -) 2. 2. Приписывается к В строка, равная вектору ci 1*B(j, -) - cj 1*B(i, -)
 Алгоритм поиска p- инвариантов Шаг 3 3. 1. Исключаются из С и B строки с индексами i I J. 3. 2. Исключается из С первый столбец. Конец алгоритма. Множество строк матрицы B есть минимальное порождающее семейство инвариантов.
Алгоритм поиска p- инвариантов Шаг 3 3. 1. Исключаются из С и B строки с индексами i I J. 3. 2. Исключается из С первый столбец. Конец алгоритма. Множество строк матрицы B есть минимальное порождающее семейство инвариантов.
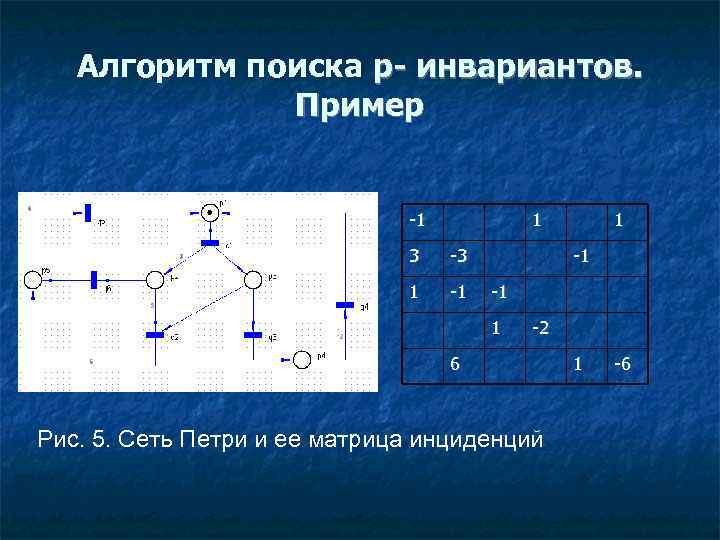 Алгоритм поиска p- инвариантов. Пример -1 1 3 -3 1 -1 -1 1 -2 6 Рис. 5. Сеть Петри и ее матрица инциденций 1 -6
Алгоритм поиска p- инвариантов. Пример -1 1 3 -3 1 -1 -1 1 -2 6 Рис. 5. Сеть Петри и ее матрица инциденций 1 -6
 Алгоритм поиска p- инвариантов. Пример Исходную информацию для алгоритма представим в виде 2 матриц: -1 1 3 -3 1 -1 -1 1 6 1 1 -2 1 1 -6 1
Алгоритм поиска p- инвариантов. Пример Исходную информацию для алгоритма представим в виде 2 матриц: -1 1 3 -3 1 -1 -1 1 6 1 1 -2 1 1 -6 1
 Литература 1. Ачасова С. М. , Бандман О. Л. Корректность параллельных вычислительных процессов. Новосибирск: Наука. Сибирское отделение, 1990. 2. Guţuleac E. Modelarea şi evaluarea performanţelor sistemelor de calcul prin Reţele Petri: Departamentul Editorial-Poligrafic al U. T. M. Chişinău, 1998.
Литература 1. Ачасова С. М. , Бандман О. Л. Корректность параллельных вычислительных процессов. Новосибирск: Наука. Сибирское отделение, 1990. 2. Guţuleac E. Modelarea şi evaluarea performanţelor sistemelor de calcul prin Reţele Petri: Departamentul Editorial-Poligrafic al U. T. M. Chişinău, 1998.
