С.44-54 С.20-28 С.5-15 Предыдущая лекция Латинские прямоугольники и




















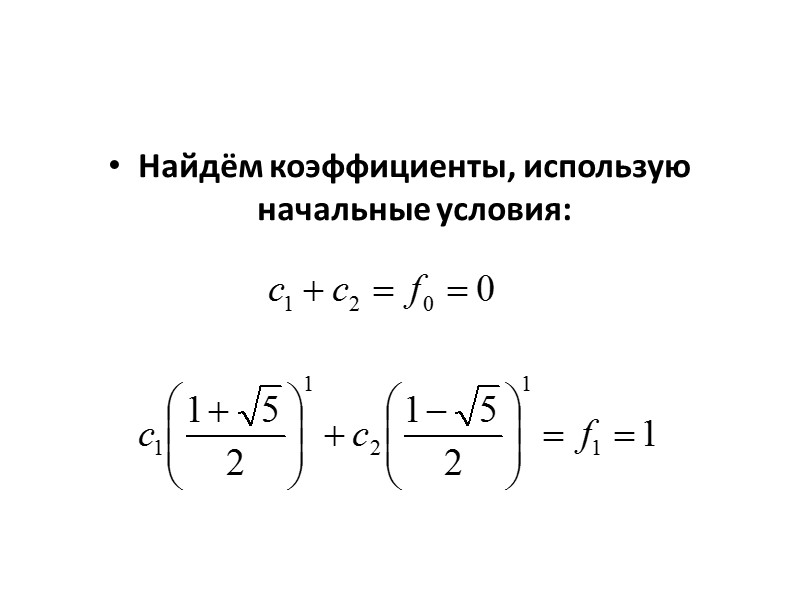

















![In[13]:= 5 ! Out[13]= 120 In[19]:= 1 ! Out[19]= 1 In[16]:= 0 ! In[13]:= 5 ! Out[13]= 120 In[19]:= 1 ! Out[19]= 1 In[16]:= 0 !](https://present5.com/presentacii/20170504/65-dm_kob_l10.2011_.ppt_images/65-dm_kob_l10.2011_.ppt_66.jpg)



65-dm_kob_l10.2011_.ppt
- Количество слайдов: 71
 С.44-54
С.44-54
 С.20-28
С.20-28
 С.5-15
С.5-15
 Предыдущая лекция Латинские прямоугольники и квадраты.
Предыдущая лекция Латинские прямоугольники и квадраты.
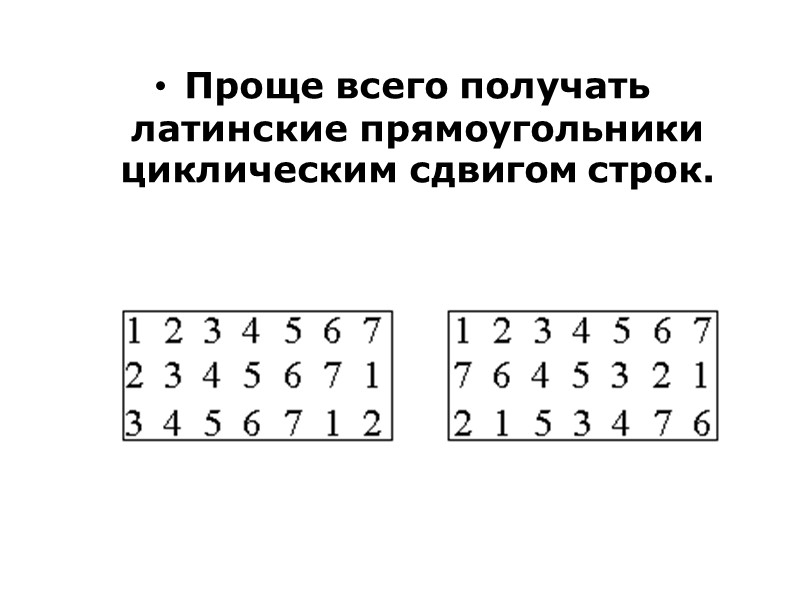
 Проще всего получать латинские прямоугольники циклическим сдвигом строк.
Проще всего получать латинские прямоугольники циклическим сдвигом строк.
 Название «латинский квадрат» берёт начало от Леонарда Эйлера, который использовал латинские буквы вместо цифр в таблице.
Название «латинский квадрат» берёт начало от Леонарда Эйлера, который использовал латинские буквы вместо цифр в таблице.
 Латинский квадрат Латинский квадрат - таблица n × n, заполненная n различными символами таким образом, чтобы в каждой строке и в каждом столбце встречались все n символов (каждый по одному разу).
Латинский квадрат Латинский квадрат - таблица n × n, заполненная n различными символами таким образом, чтобы в каждой строке и в каждом столбце встречались все n символов (каждый по одному разу).
 Греко-латинский квадрат
Греко-латинский квадрат
 Греко-латинский квадрат
Греко-латинский квадрат
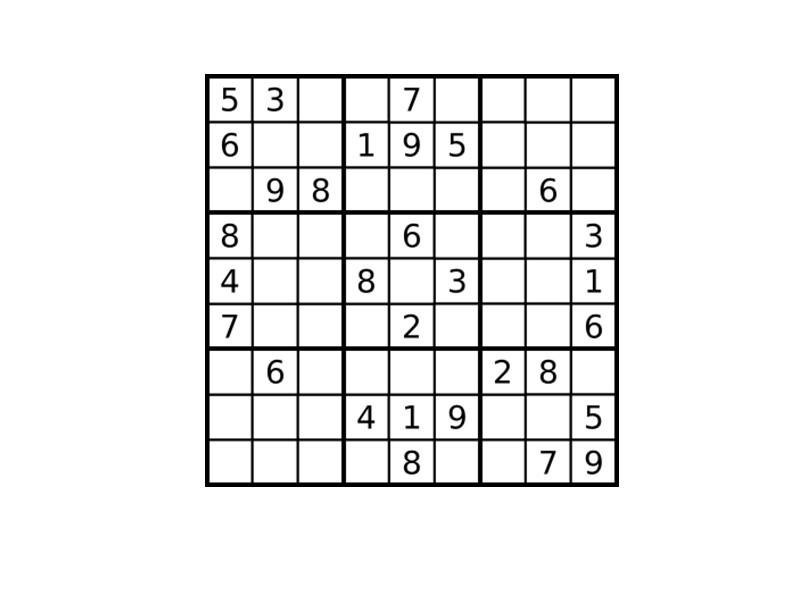
 Судоку (яп. 数独 ) — головоломка. В переводе с японского «су» — «цифра», «доку» — «стоящая отдельно». Иногда судоку называют «магическим квадратом», что не верно, так как судоку является латинским квадратом 9-го порядка.
Судоку (яп. 数独 ) — головоломка. В переводе с японского «су» — «цифра», «доку» — «стоящая отдельно». Иногда судоку называют «магическим квадратом», что не верно, так как судоку является латинским квадратом 9-го порядка.

 Количество возможных комбинаций в судоку 9x9 составляет по расчётам 6 670 903 752 021 072 936 960.
Количество возможных комбинаций в судоку 9x9 составляет по расчётам 6 670 903 752 021 072 936 960.
 Магический квадрат
Магический квадрат
 На известной гравюре Альбрехта Дюрера «Меланхолия» (1514г. – почти полтысячи лет назад ):
На известной гравюре Альбрехта Дюрера «Меланхолия» (1514г. – почти полтысячи лет назад ):
 Маги́ческий, или волше́бный квадра́т — это квадратная таблица , заполненная n n числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n n.
Маги́ческий, или волше́бный квадра́т — это квадратная таблица , заполненная n n числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n n.
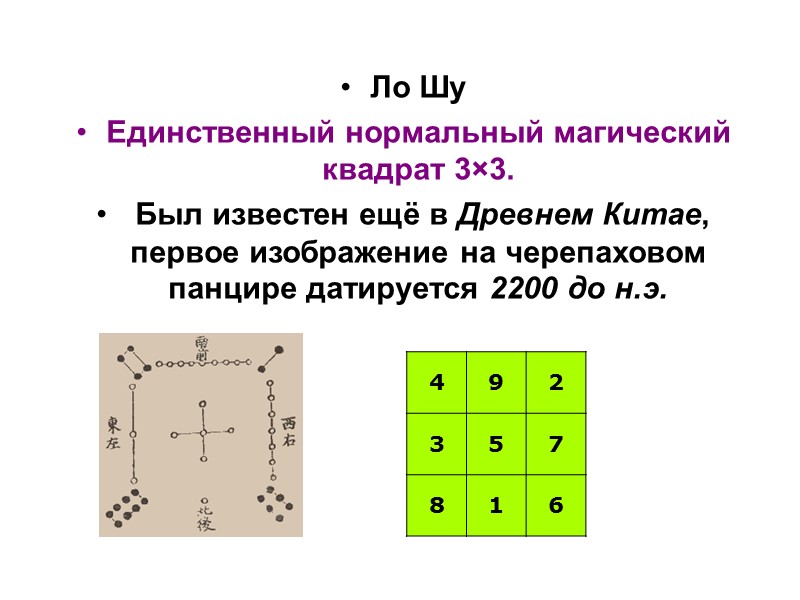
 Ло Шу Единственный нормальный магический квадрат 3×3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 до н.э.
Ло Шу Единственный нормальный магический квадрат 3×3. Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 до н.э.
 Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой
 Магический квадрат послужил предвестником нового направления в комбинаторике – оно рассматривает так называемые блок схемы – таблицы из систем чисел или множеств, которые удовлетворяют сразу большому количеству очень жёстких ограничений. Настолько жёстких, что речь идёт уже не о перечислении возможных вариантов, а о самом существовании такой схемы.
Магический квадрат послужил предвестником нового направления в комбинаторике – оно рассматривает так называемые блок схемы – таблицы из систем чисел или множеств, которые удовлетворяют сразу большому количеству очень жёстких ограничений. Настолько жёстких, что речь идёт уже не о перечислении возможных вариантов, а о самом существовании такой схемы.
 Конечные проективные плоскости
Конечные проективные плоскости
 Проективная плоскость — это множества точек и прямых и такое отношение инцидентности, что - для любых двух различных точек существует единственная инцидентная им прямая; - для любых двух различных прямых существует единственная инцидентная им точка — точка пересечения; - существуют такие четыре точки, что прямая, инцидентная двум из них, не инцидентна ни одной из двух других.
Проективная плоскость — это множества точек и прямых и такое отношение инцидентности, что - для любых двух различных точек существует единственная инцидентная им прямая; - для любых двух различных прямых существует единственная инцидентная им точка — точка пересечения; - существуют такие четыре точки, что прямая, инцидентная двум из них, не инцидентна ни одной из двух других.
 Плоскость Фано Плоскость Фано имеет 7 точек и 7прямых. Отношение инцидентности на плоскости Фано задано следующей таблицей: 1 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 0 1 0 0 1 1 0 1 0 0
Плоскость Фано Плоскость Фано имеет 7 точек и 7прямых. Отношение инцидентности на плоскости Фано задано следующей таблицей: 1 1 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 1 0 1 0 0 1 1 0 1 0 0 1 1 0 1 0 0
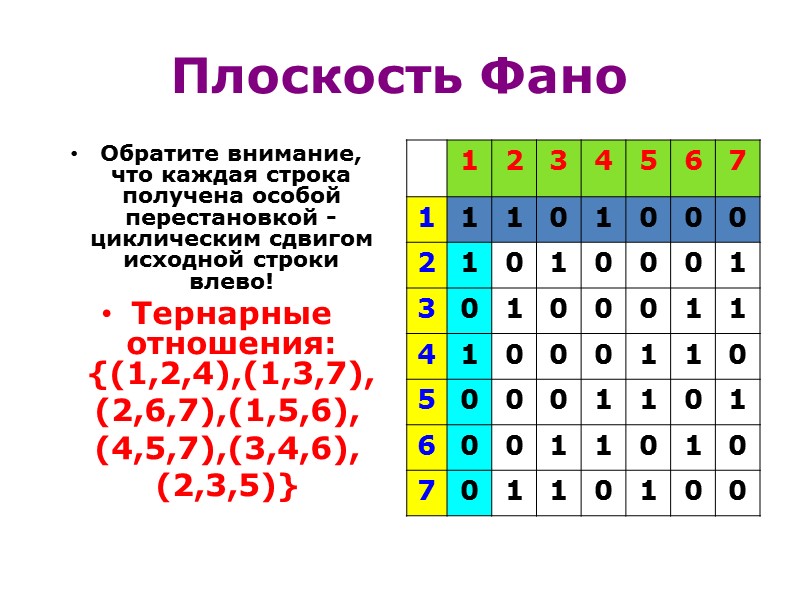
 Плоскость Фано Обратите внимание, что каждая строка получена особой перестановкой - циклическим сдвигом исходной строки влево! Тернарные отношения: {(1,2,4),(1,3,7), (2,6,7),(1,5,6), (4,5,7),(3,4,6), (2,3,5)}
Плоскость Фано Обратите внимание, что каждая строка получена особой перестановкой - циклическим сдвигом исходной строки влево! Тернарные отношения: {(1,2,4),(1,3,7), (2,6,7),(1,5,6), (4,5,7),(3,4,6), (2,3,5)}
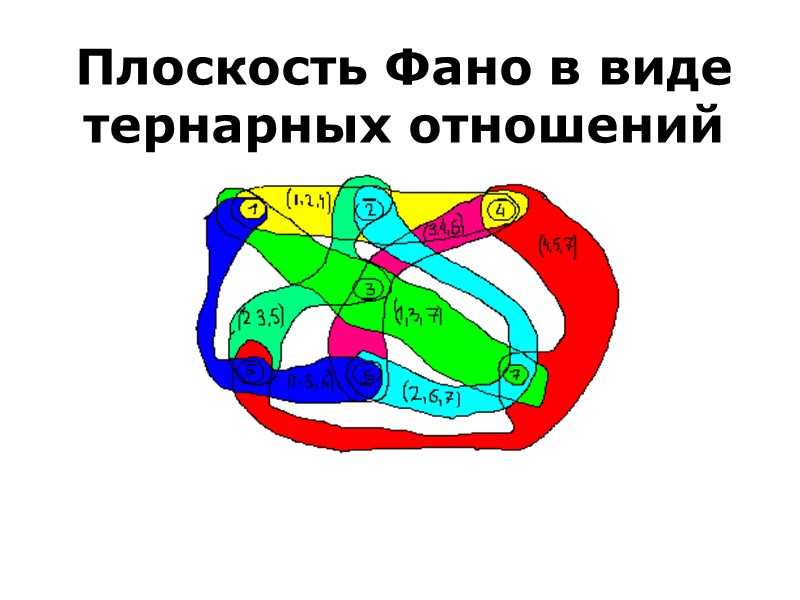
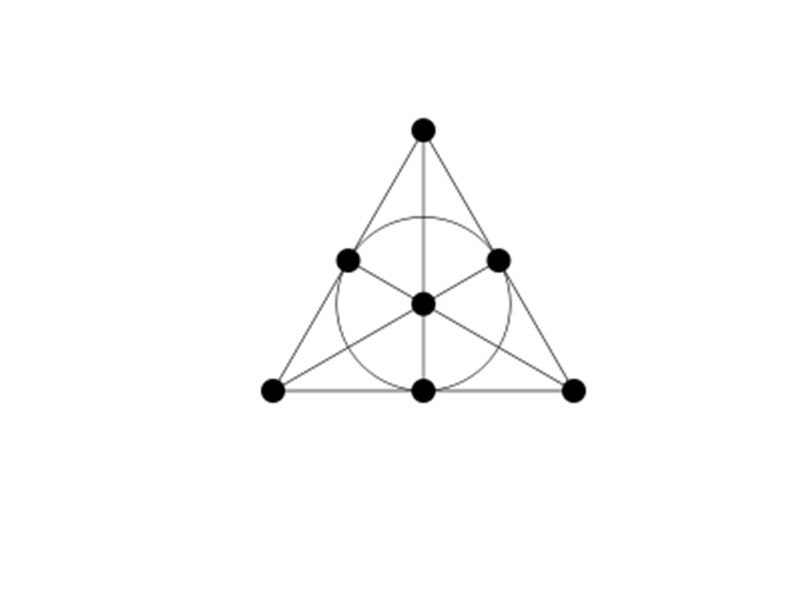
 Плоскость Фано в виде тернарных отношений
Плоскость Фано в виде тернарных отношений
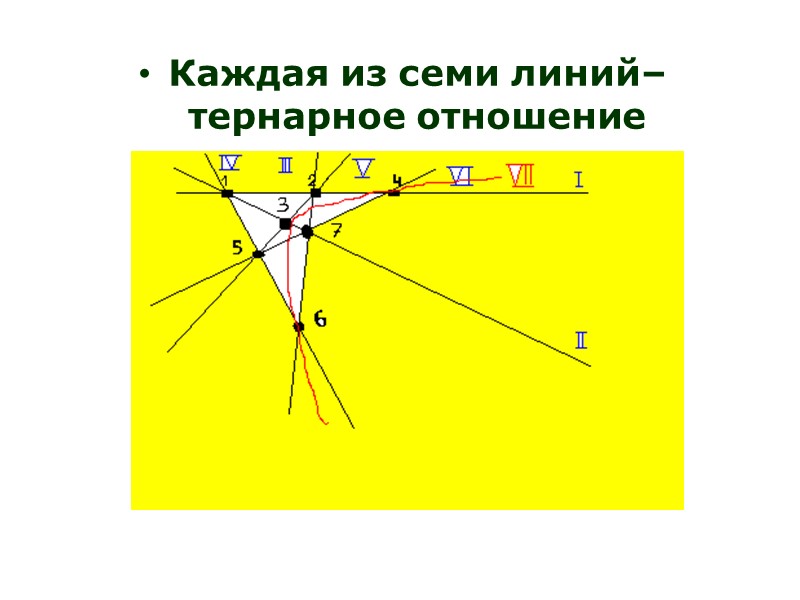
 Каждая из семи линий– тернарное отношение
Каждая из семи линий– тернарное отношение

 Палиндром: SATOR AREPO TENET OPERA ROTAS (лат. Сеятель Арепо с трудом держит колеса)
Палиндром: SATOR AREPO TENET OPERA ROTAS (лат. Сеятель Арепо с трудом держит колеса)
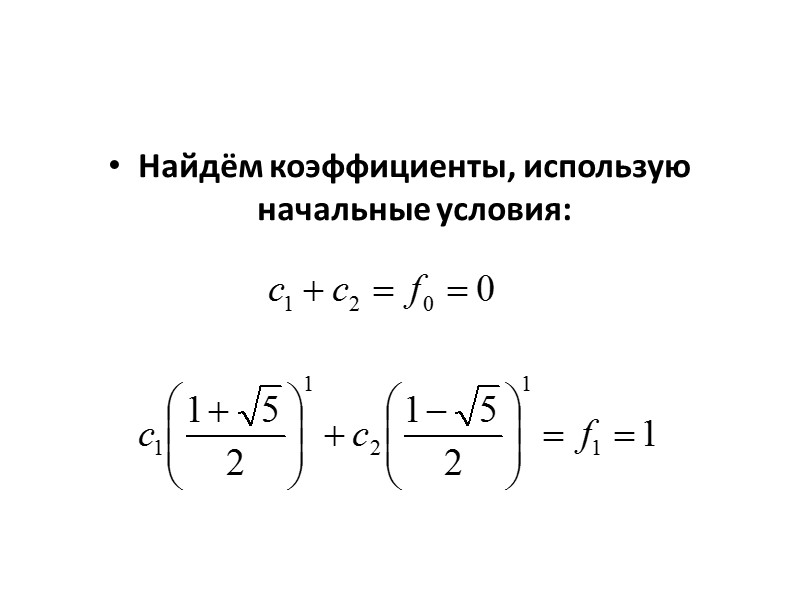 Лекция 10 Метод рекуррентных соотношений.
Лекция 10 Метод рекуррентных соотношений.
 Метод рекуррентных соотношений состоит в том, что решение комбинаторной задачи с n предметами выражается через решение аналогичной задачи с меньшим числом предметов с помощью некоторого соотношения, которое называется рекуррентным. Пользуясь этим соотношением, искомую величину можно вычислить алгоритмически, исходя из того, что для небольшого количества предметов решение задачи легко находится.
Метод рекуррентных соотношений состоит в том, что решение комбинаторной задачи с n предметами выражается через решение аналогичной задачи с меньшим числом предметов с помощью некоторого соотношения, которое называется рекуррентным. Пользуясь этим соотношением, искомую величину можно вычислить алгоритмически, исходя из того, что для небольшого количества предметов решение задачи легко находится.
 Рекуррентным называют соотношение, в котором для вычисления некоторого члена числовой последовательности используют значения предыдущих членов.
Рекуррентным называют соотношение, в котором для вычисления некоторого члена числовой последовательности используют значения предыдущих членов.
 Чи́сла Фибона́ччи — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 …
Чи́сла Фибона́ччи — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 …
 Решение рекуррентных соотношений Пусть Тогда
Решение рекуррентных соотношений Пусть Тогда
 Разделим обе части выражения на получим
Разделим обе части выражения на получим
 Получим Поскольку то
Получим Поскольку то
 Найдём коэффициенты, использую начальные условия:
Найдём коэффициенты, использую начальные условия:
 Таким образом:
Таким образом:
 Поэтому
Поэтому
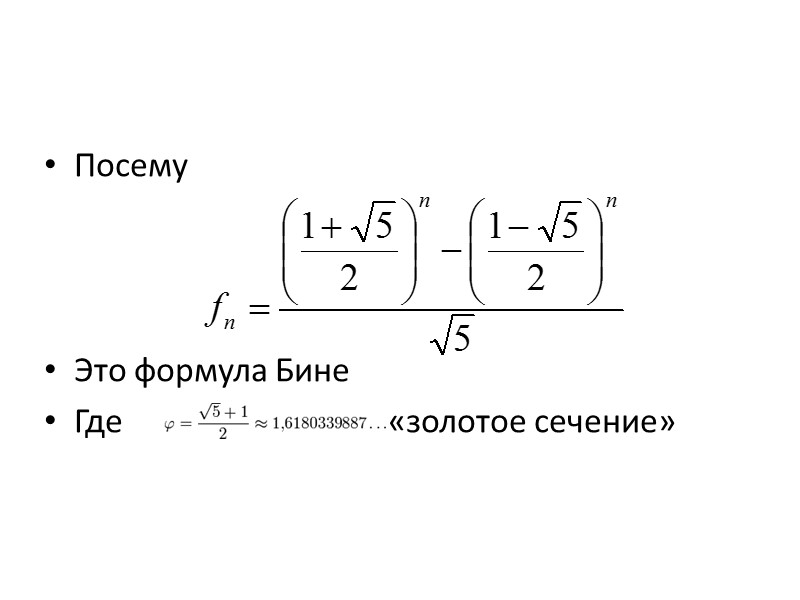
 Посему Это формула Бине Где «золотое сечение»
Посему Это формула Бине Где «золотое сечение»
 Решение рекуррентных соотношений В общем случае линейное рекуррентное соотношение с постоянными коэффициентами имеет вид
Решение рекуррентных соотношений В общем случае линейное рекуррентное соотношение с постоянными коэффициентами имеет вид
 Где Постоянные коэффициенты, начальные значения
Где Постоянные коэффициенты, начальные значения
 Решение находим в виде Подставляя в исходное выражение получаем полином k-ой степени (после деления на
Решение находим в виде Подставляя в исходное выражение получаем полином k-ой степени (после деления на
 Это уравнение имеет k корней Тогда общее решение имеет вид Где неизвестные коэффициенты находят по начальным условиям, составляя соответствующую систему линейных уравнений
Это уравнение имеет k корней Тогда общее решение имеет вид Где неизвестные коэффициенты находят по начальным условиям, составляя соответствующую систему линейных уравнений
 СКМ для комбинаторных вычислений
СКМ для комбинаторных вычислений
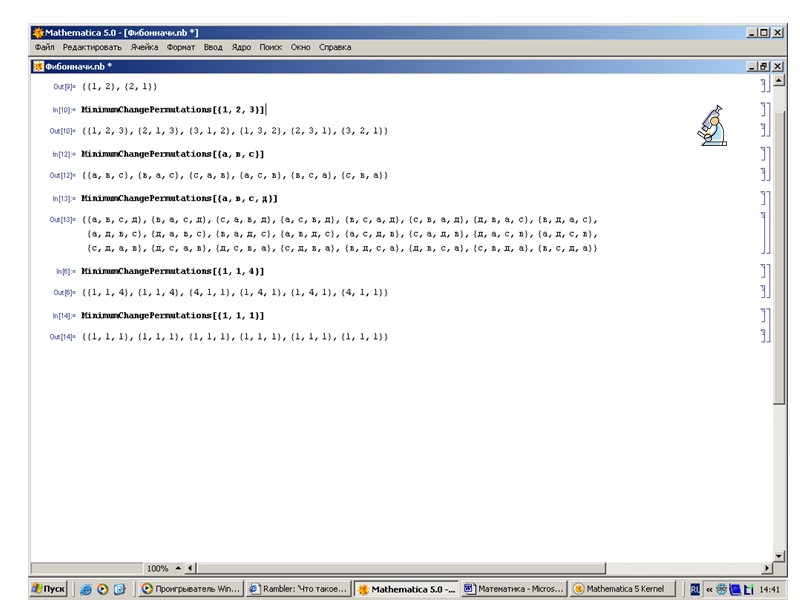
 В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research,Inc. – пакет расширения «Дискретная математика» (DiscreteMath) – комбинаторика и ее функции (Combinatorica, CombinatorialFunctions)
В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3,4) фирмы Wolfram Research,Inc. – пакет расширения «Дискретная математика» (DiscreteMath) – комбинаторика и ее функции (Combinatorica, CombinatorialFunctions)
 В справочнике пакета Mathematica 5.1 закладка The Mathematica book, в ней – Advanced Mathematics, далее – Mathematics Functions, Combinatorial Functions:
В справочнике пакета Mathematica 5.1 закладка The Mathematica book, в ней – Advanced Mathematics, далее – Mathematics Functions, Combinatorial Functions:




![>In[13]:= 5 ! Out[13]= 120 In[19]:= 1 ! Out[19]= 1 In[16]:= 0 ! >In[13]:= 5 ! Out[13]= 120 In[19]:= 1 ! Out[19]= 1 In[16]:= 0 !](https://present5.com/presentacii/20170504/65-dm_kob_l10.2011_.ppt_images/65-dm_kob_l10.2011_.ppt_66.jpg) In[13]:= 5 ! Out[13]= 120 In[19]:= 1 ! Out[19]= 1 In[16]:= 0 ! Out[16]= 1 In[14]:= 4 !! Out[14]= 8 In[15]:= 5 !! Out[15]=15 In[17]:= 1!! Out[17]= 1 In[20]:= 10 ! Out[20]= 3628800 In[26]:= 20 ! Out[26]= 2432902008176640000 In[27]:= 30 ! Out[27]= 2652528598121910586363308480000000 --------------------------------------------------------------- In[21]:= 100 ! Out[21]= 93326215443944152681692238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
In[13]:= 5 ! Out[13]= 120 In[19]:= 1 ! Out[19]= 1 In[16]:= 0 ! Out[16]= 1 In[14]:= 4 !! Out[14]= 8 In[15]:= 5 !! Out[15]=15 In[17]:= 1!! Out[17]= 1 In[20]:= 10 ! Out[20]= 3628800 In[26]:= 20 ! Out[26]= 2432902008176640000 In[27]:= 30 ! Out[27]= 2652528598121910586363308480000000 --------------------------------------------------------------- In[21]:= 100 ! Out[21]= 93326215443944152681692238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
 Обратим внимание на факториал числа 100 – это 158-разрядное число!
Обратим внимание на факториал числа 100 – это 158-разрядное число!
 Как проводить вычисления? Выделяем пример выполнения требуемой функции и копируем в новый открытый файл результатов, редактируем, а затем инициируем вычисления, нажав клавишу Shift с клавишей Enter.
Как проводить вычисления? Выделяем пример выполнения требуемой функции и копируем в новый открытый файл результатов, редактируем, а затем инициируем вычисления, нажав клавишу Shift с клавишей Enter.

