Розподіл  2 (розподіл Пірсона) Нехай маємо n

Розподіл  2 (розподіл Пірсона) Нехай маємо n незалежних випадкових величин 1, 2, ..., n, розподілених за стандартним нормальним законом. Тоді випадкова величина розподілена за законом, що називається “розподіл 2” або “розподіл Пірсона”..

2 – розподіл залежить тільки від n Число n називається числом ступенів вільності

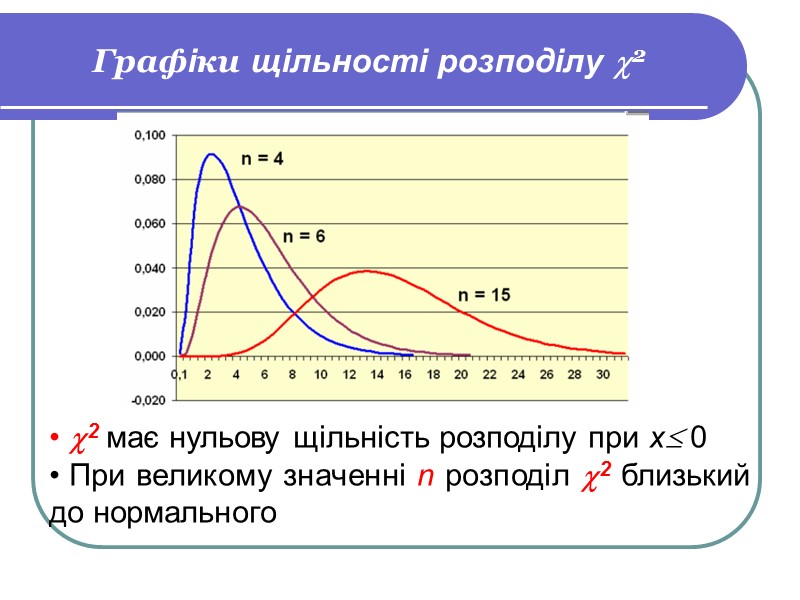
Графіки щільності розподілу 2 2 має нульову щільність розподілу при х 0 При великому значенні n розподіл 2 близький до нормального

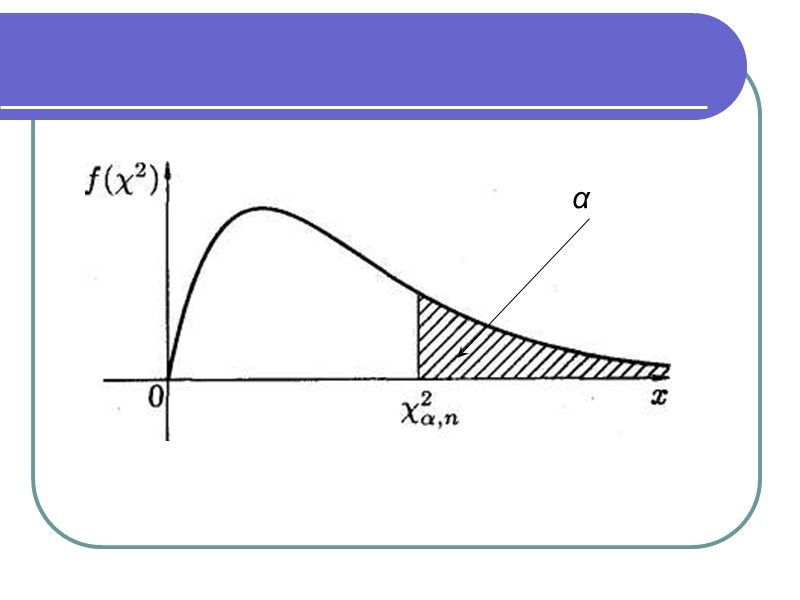
На практиці, як правило, використовують не щільність ймовірності, а квантилі розподілу. Квантилем розподілу 2, що відповідає рівню значущості , називається таке значення 2, при якому P(2 > 2) = .

α

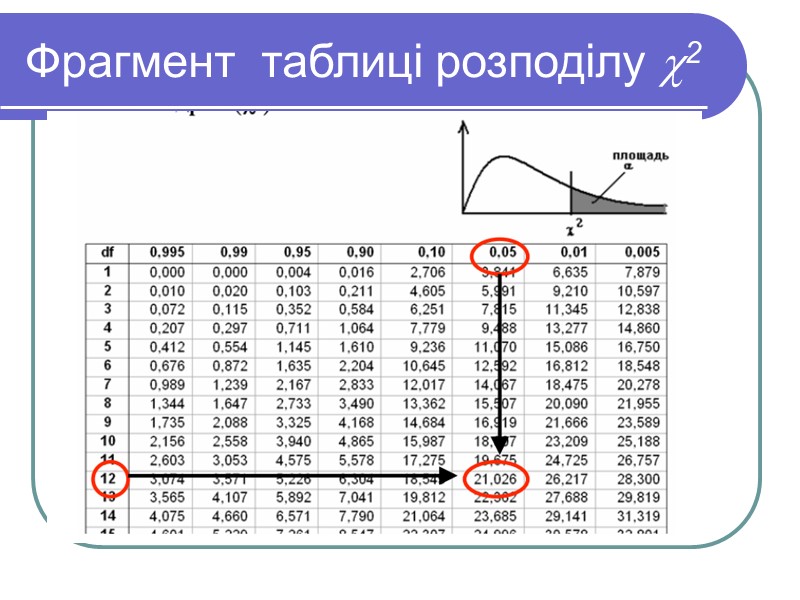
Фрагмент таблиці розподілу 2

Функції Excel P(2 > 2)= XИ2PACП(2; ступені_вільності) – повертає ймовірність α. XИ2ОБP(ймовірність; ступені_вільності) – повертає значення 2.

Розподіл Стьюдента (t – розподіл) Закон розподілу випадкової величини t називається законом розподілу Стьюдента з k ступенями вільності  і  – незалежні випадкові величини, причому  – має стандартній нормальний розподіл, а  розподілена за законом 2 c k ступенями вільності.

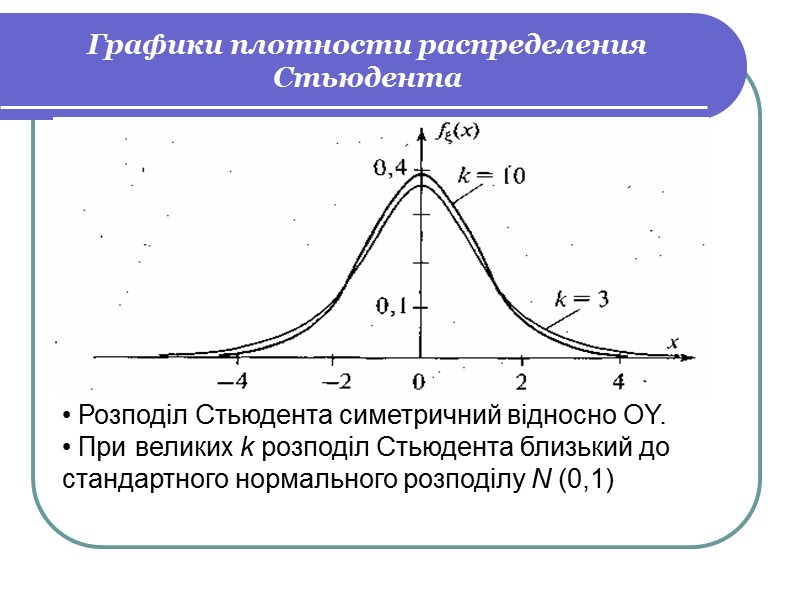
Графики плотности распределения Стьюдента Розподіл Стьюдента симетричний відносно OY. При великих k розподіл Стьюдента близький до стандартного нормального розподілу N (0,1)

Таблиці розподілу Стьюдента дозволяють при даному числі ступенів вільності k за ймовірністю α визначити значення tα, для якого виконується співвідношення P( t  > tα) = α.

Функції Excel СТЬЮДРАСП( tα ; ступені_вільності; ознака) – повертає ймовірність  Якщо ознака = 1, то функція СТЬЮДРАСП повертає однобічний розподіл (P(t > t α) = α ). Якщо ознака = 2, то функція СТЬЮДРАСП повертає двосторонній розподіл P(  t  > tα ) = α

СТЬЮДРАСПОБР( ймовірність; ступені_вільності) – повертає значення tα для двостороннього розподілу Стьюдента, що є розв’язком рівняння P(  t  > tα ) = α .

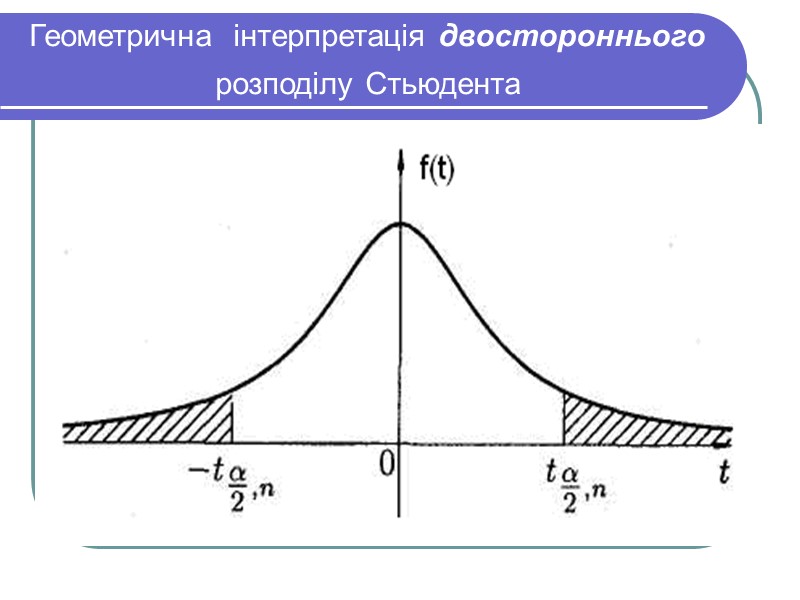
Геометрична інтерпретація двостороннього розподілу Стьюдента

Якщо потрібно розв’язати рівняння СТЬЮДРАСПОБР (1- ; ступені_вільності).

Довірчі інтервали

17 Нехай розподіл ознаки Х, генеральної сукупності, задається своєю функцією розподілу, з невідомим параметром Q. Для визначення параметра Q виходять із даних вибіркової сукупності х1, х2, …, хn.

Тоді оцінкою невідомого параметра Q будемо називати будь-яку функцію (інша назва – статистика) результатів спостережень над випадковою величиною Х, за допомогою якої судять про невідоме значення параметра Q.

Якщо оцінка параметра Q генеральної сукупності визначається одним числом, її називають точковою. Середнє значення – точкова оцінка математичного сподівання, вибіркова дисперсія – точкова оцінка дисперсії і т.д Однак точкова оцінка Q* є лише наближеним значенням невідомого параметра Q, для вибірки малого об’єму може сильно відрізнятися від невідомого параметру Q.

Щоб мати більш точну та надійну оцінку параметра Q використовують, так звану, інтервальну оцінку. Інтервальною називають оцінку, що визначається двома числами – кінцями інтервалу

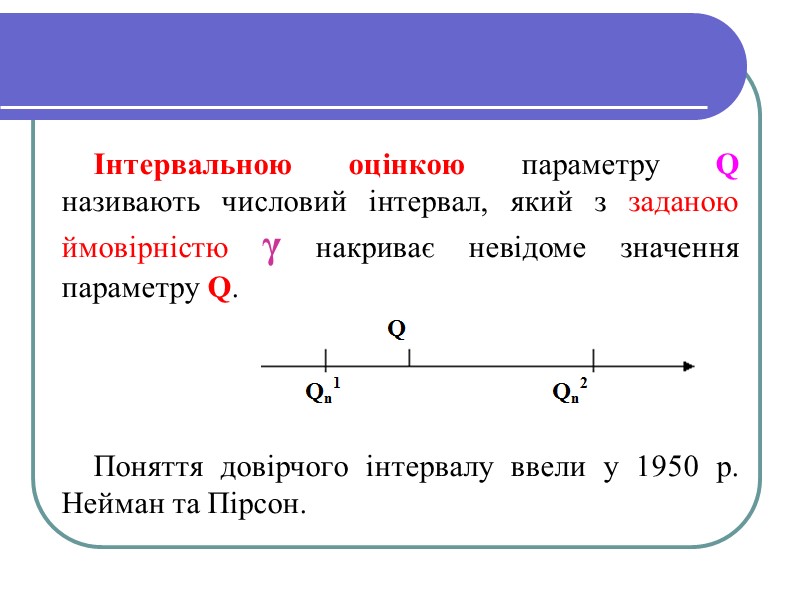
Інтервальною оцінкою параметру Q називають числовий інтервал, який з заданою ймовірністю γ накриває невідоме значення параметру Q. Поняття довірчого інтервалу ввели у 1950 р. Нейман та Пірсон.

Нехай знайдена за даними вибірки точкова характеристика Q* , яка служить оцінкою невідомого параметра Q. Будемо вважати Q=const. Q* тим точніше визначає Q, чим менше абсолютна величина | Q - Q* | <δ . δ – характеризує точність оцінки.

Надійністю оцінки Q по Q* називають ймовірність γ P( | Q- Q* | <δ ) = γ. Найчастіше задають γ = 0,95; 0,99 і 0,999.

Перейшовши до подвійної нерівності, отримаємо P(Q* - δ < Q < Q* + δ ) = γ. Довірчим називають інтервал (Q* - δ ; Q* + δ ) , що покриває невідомий параметр із заданою надійністю γ.

Довірчий інтервал для оцінки математичного сподівання нормального розподілу при невідомому  Нехай кількісна ознака Х генеральної сукупності розподілена нормально і  невідоме. Побудуємо випадкову величину яка має розподіл Стьюдента з k=n-1 ступенями вільності, де m – математичне сподівання; - середнє значення; S - стандартне відхилення.

Визначимо значення t з рівняння де  – задана надійність. t визначаємо за допомогою таблиці, або функції Excel. t = СТЬЮДРАСПОБР (1- γ; n-1)

Підставимо значення Т. Отримаємо

Користуючись розподілом Стьюдента, ми знайшли довірчий інтервал що покриває невідомий параметр m з надійністю γ.

Межі інтервалу знаходяться за вибірковими даними та є випадковими величинами. Також не важко побачити, що величина вибіркового інтервалу залежить від об’єму вибірки (зменшується із зростанням n) та від значення довірчої ймовірності γ (збільшується при наближенні її до 1).

Приклад. За даними 9 незалежних вимірювань фізичної величини знайдене =42,319 і величини S=5,0. Оцінити істинне значення вимірюваної величини з надійністю γ=0,95.

Істинне значення вимірюваної величини дорівнює математичному сподіванню, тому задача зводиться до оцінки математичного сподівання при невідомому σ за допомогою довірчого інтервалу: який покриває m із заданою надійністю γ=0,95.

Знаходимо t= СТЬЮДРАСПОБР(1-0,95; 9-1), знаходимо, що t =2,31, =2,31* =3,85. Отже, довірчий інтервал, що з надійністю γ=0,95 покриває істинне значення вимірюваної величини: 38,469< m <46,169.

Для n=25, tγ =2,09, отже довірчий інтервал, що з надійністю γ=0,95 покриває істинне значення вимірюваної величини 42,319 – 3,48< a <42,319 + 3,48 , 38,839

Довірчий інтервал для середнього квадратичного відхилення (нормальний розподіл) Можна показати, що якщо MX=m невідоме, то довірчий інтервал для середнього квадратичного відхилення має вигляд:

Таблиця для випадкової величини 2 звичайно задається розв’язком рівняння За таблицею для заданої величини q і за числом ступенів вільності n-1 визначаємо q2 (функція EXCEL ХИ2ОБР(q; n-1)).

Приклад. За даними 20 вимірювань знайдене виправлене середньоквадратичне відхилення S=0,12. Знайти точність вимірів з надійністю 0,98.

Точність вимірів характеризується середнім квадратичним відхиленням σ випадкових помилок. Тому задача зводиться до знаходження довірчого інтервалу, що покриває σ із заданою надійністю (0,98).

Використовуючи функцію ХИ2ОБР(q, n-1), знайдемо 12 і 22 . Для ступенів вільності n - 1=19 і ймовірності α2=(1-0,98)/2=0,01 знаходимо 22 =36,2, а потім для n - 1=19 і ймовірності α1=(1+0,98)/2=0,99 знаходимо 12 =7,63. 22 =ХИ20БР(0,01; 19)=36,2 ; 12 =ХИ20БР(0,99;19)=7,63.

Знаходимо Шуканий довірчий інтервал (0,09;0,19).