Решение заданий площади частей круга по материалам





ploschady_chastey_kruga.pptx
- Размер: 692.3 Кб
- Автор:
- Количество слайдов: 12
Описание презентации Решение заданий площади частей круга по материалам по слайдам
 Решение заданий площади частей круга по материалам открытого банка задач ЕГЭ по математике
Решение заданий площади частей круга по материалам открытого банка задач ЕГЭ по математике
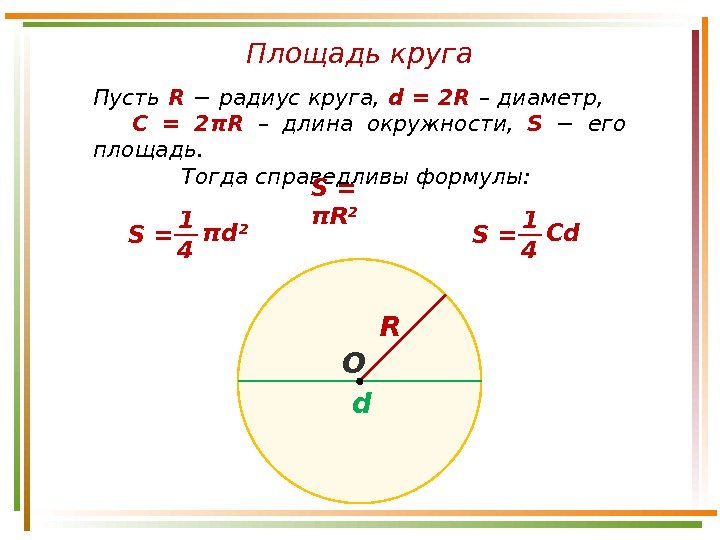
 Площадь круга Пусть R − радиус круга, d = 2 R – диаметр, С = 2πR – длина окружности, S − его площадь. Тогда справедливы формулы: S = πR 2 R d Сd 4 1 S =πd 2 4 1 S = О
Площадь круга Пусть R − радиус круга, d = 2 R – диаметр, С = 2πR – длина окружности, S − его площадь. Тогда справедливы формулы: S = πR 2 R d Сd 4 1 S =πd 2 4 1 S = О
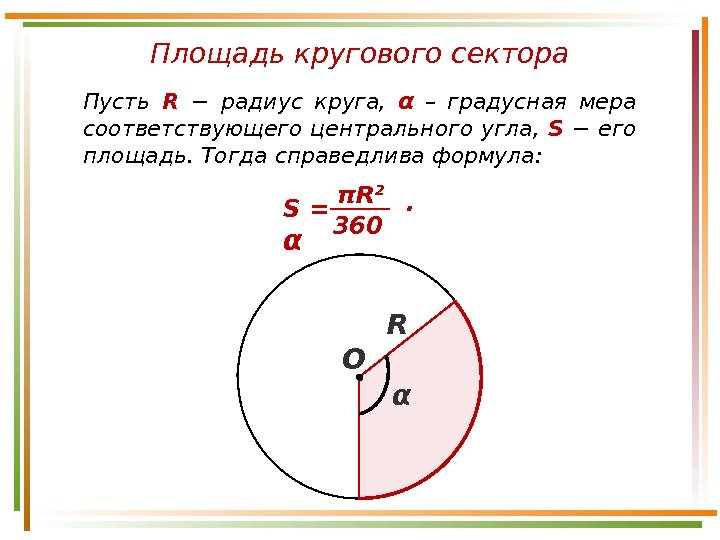
 Площадь кругового сектора Пусть R − радиус круга, α – градусная мера соответствующего центрального угла, S − его площадь. Тогда справедлива формула: RπR 2 360 S = · α αО
Площадь кругового сектора Пусть R − радиус круга, α – градусная мера соответствующего центрального угла, S − его площадь. Тогда справедлива формула: RπR 2 360 S = · α αО
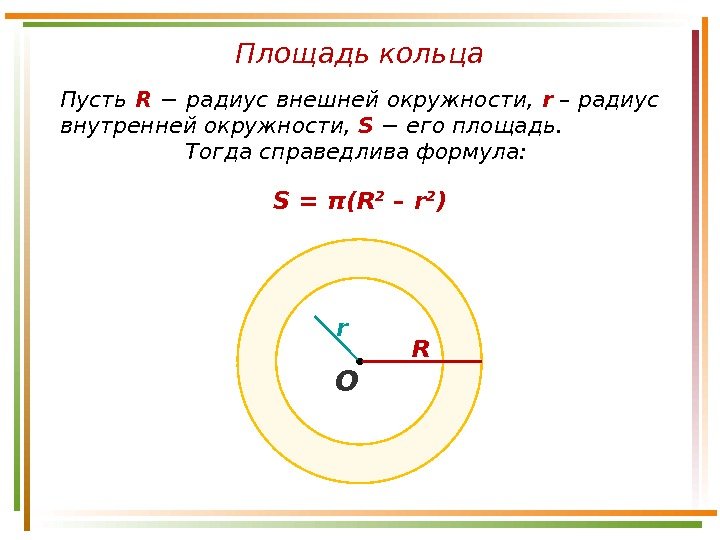
 Площадь кольца Пусть R − радиус внешней окружности, r – радиус внутренней окружности, S − его площадь. Тогда справедлива формула: О Rr. S = π(R 2 – r 2 )
Площадь кольца Пусть R − радиус внешней окружности, r – радиус внутренней окружности, S − его площадь. Тогда справедлива формула: О Rr. S = π(R 2 – r 2 )
 Задания открытого банка задач1. Найдите площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см× 1 см. В ответе запишите S/π. Ответ: 11, 25. Решение : 3 3 R по теореме Пифагора: 1 см 2 8 5 RπSSкругасектора 1833 222 R. , π ππ S сектора
Задания открытого банка задач1. Найдите площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см× 1 см. В ответе запишите S/π. Ответ: 11, 25. Решение : 3 3 R по теореме Пифагора: 1 см 2 8 5 RπSSкругасектора 1833 222 R. , π ππ S сектора
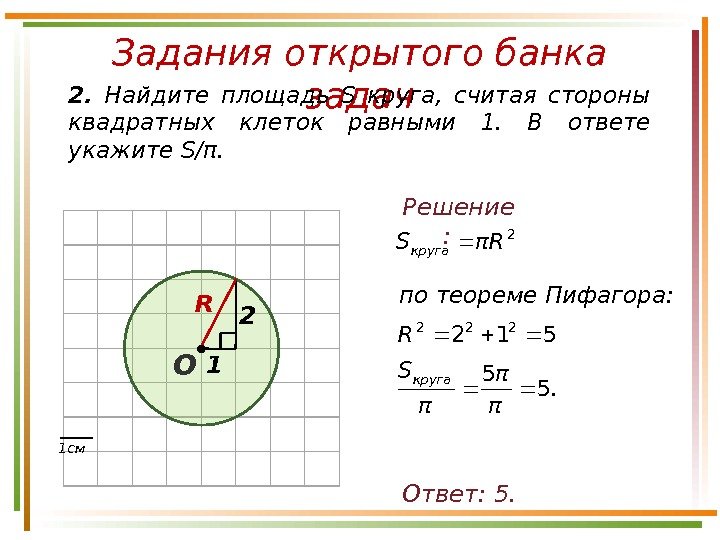
 Задания открытого банка задач2. Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/π. Ответ: 5. Решение : по теореме Пифагора: 1 см 2 R 1 О 2 RπSкруга 512 222 R. π π π S круга
Задания открытого банка задач2. Найдите площадь S круга, считая стороны квадратных клеток равными 1. В ответе укажите S/π. Ответ: 5. Решение : по теореме Пифагора: 1 см 2 R 1 О 2 RπSкруга 512 222 R. π π π S круга
 Задания открытого банка задач3. Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см× 1 см. В ответе запишите S/π. Ответ: 13. Решение : по теореме Пифагора: 3 3 R 1 см 1 2 rкруга. мкруга. б. SSS 1833 222 R . π π π S 13 518 512 222 r 2222 r. RπrπRπS
Задания открытого банка задач3. Найдите (в см 2 ) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см× 1 см. В ответе запишите S/π. Ответ: 13. Решение : по теореме Пифагора: 3 3 R 1 см 1 2 rкруга. мкруга. б. SSS 1833 222 R . π π π S 13 518 512 222 r 2222 r. RπrπRπS
 Задания открытого банка задач4. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 12. Найдите площадь заштрихованной фигуры. Ответ: 180. Решение : Rr 2 2 r R rπ Rπ S S круга. м круга. б 164 2 2 r R 16 круга. м круга. б S S 192121616 круга. мкруга. б. SS круга. мкруга. бкольца. SSS 18012192 кольца. S
Задания открытого банка задач4. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 12. Найдите площадь заштрихованной фигуры. Ответ: 180. Решение : Rr 2 2 r R rπ Rπ S S круга. м круга. б 164 2 2 r R 16 круга. м круга. б S S 192121616 круга. мкруга. б. SS круга. мкруга. бкольца. SSS 18012192 кольца. S
 Задания открытого банка задач5. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Ответ: 21. Решение : Rr 2 2 r R rπ Rπ S S круга. м круга. б 4 25 2 2 r R 4 25 круга. м круга. б S S 254 4 25 круга. мкруга. б. SSS 21425 S
Задания открытого банка задач5. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 4. Найдите площадь заштрихованной фигуры. Ответ: 21. Решение : Rr 2 2 r R rπ Rπ S S круга. м круга. б 4 25 2 2 r R 4 25 круга. м круга. б S S 254 4 25 круга. мкруга. б. SSS 21425 S
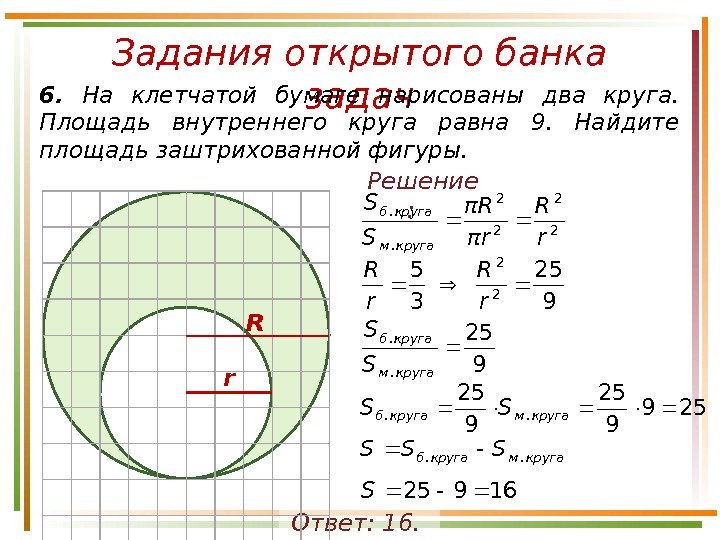
 Задания открытого банка задач6. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры. Ответ: 16. Решение : R r 2 2 r R rπ Rπ S S круга. м круга. б 9 25 3 5 2 2 r R 9 25 круга. м круга. б S S 259 9 25 круга. мкруга. б. SSS 16925 S
Задания открытого банка задач6. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры. Ответ: 16. Решение : R r 2 2 r R rπ Rπ S S круга. м круга. б 9 25 3 5 2 2 r R 9 25 круга. м круга. б S S 259 9 25 круга. мкруга. б. SSS 16925 S
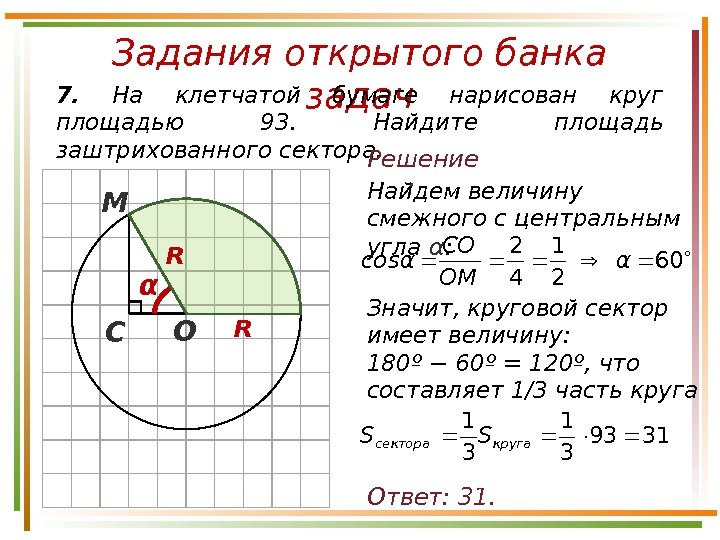
 Задания открытого банка задач7. На клетчатой бумаге нарисован круг площадью 93. Найдите площадь заштрихованного сектора. Ответ: 31. Решение : R Найдем величину смежного с центральным угла α : О СМ α Значит, круговой сектор имеет величину: 180º − 60º = 120º, что составляет 1/3 часть круга. R 3193 3 1 кругасектора. SS 60 2 1 4 2 αα ОМ СО cos
Задания открытого банка задач7. На клетчатой бумаге нарисован круг площадью 93. Найдите площадь заштрихованного сектора. Ответ: 31. Решение : R Найдем величину смежного с центральным угла α : О СМ α Значит, круговой сектор имеет величину: 180º − 60º = 120º, что составляет 1/3 часть круга. R 3193 3 1 кругасектора. SS 60 2 1 4 2 αα ОМ СО cos
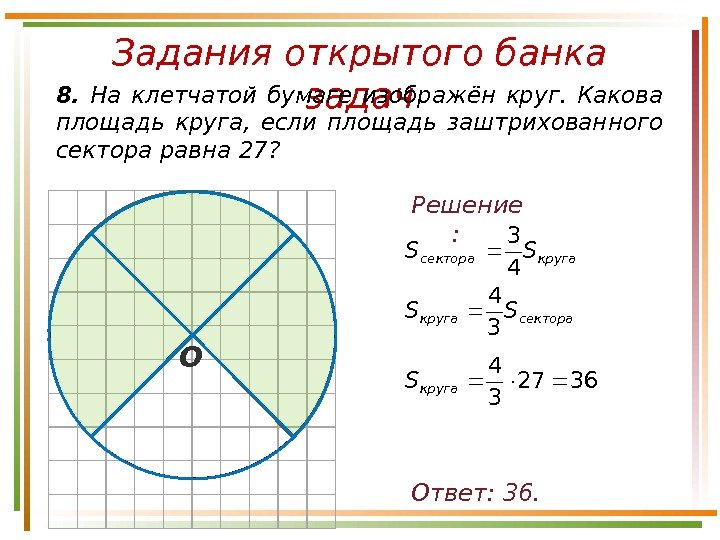
 Задания открытого банка задач8. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27? Ответ: 36. Решение : Округасектора. SS 4 3 секторакруга. SS 3 4 3627 3 4 круга. S
Задания открытого банка задач8. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 27? Ответ: 36. Решение : Округасектора. SS 4 3 секторакруга. SS 3 4 3627 3 4 круга. S
