Л5_Реляционная модель_Нормализация.ppt
- Количество слайдов: 33

Реляционная модель. Реляционная алгебра. Нормализация.

Реляционная модель данных К основным достоинствам реляционной модели относят: Ø Наличие небольшого набора абстракций, которые позволяют моделировать предметную область и допускают точные формальные определения. Ø Наличие простого и достаточно мощного математического аппарата, опирающего на теорию множеств и математическую логику и обеспечивающего теоретический базис реляционного подхода к организации баз данных. Ø Возможность ненавигационного манипулирования данными без необходимости знания конкретной физической организации баз данных во внешней памяти.

Отношения N-арным отношением R называют подмножество декартова произведения D 1 x D 2 x. . . x Dn множеств D 1, D 2, . . . , Dn ( n > 1 ), необязательно различных. Исходные множества D 1, D 2, . . . , Dn называют в модели доменами. D 1 x D 2 x. . . x Dn — полное декартово произведение, т. е. набор всевозможных сочетаний из n элементов каждое, где каждый элемент берется из своего домена. Например, три домена: D 1 — три фамилии, D 2 — набор из двух дисциплин и D 3 — набор из трех оценок. Допустим, содержимое доменов следующее: D 1 = {Иванов, Крылов, Степанов}; D 2 = {Теория автоматов, Базы данных} ; D 3 = {3, 4, 5}

Отношения Тогда полное декартово произведение содержит набор из 18 троек, где первый элемент — это одна из фамилий, второй — это название одной из учебных дисциплин, а третий — одна из оценок. <Иванов, Теория автоматов, 3>; <Иванов, Теория автоматов, 4>; <Иванов, Теория автоматов, 5> <Крылов, Теория автоматов, 3>; <Крылов, Теория автоматов, 4>; <Крылов, Теория автоматов, 5>; <Степанов, Теория автоматов, 3>; <Степанов, Теория автоматов, 4>; <Степанов, Теория автоматов, 5>; <Иванов, Базы данных, 3>; <Иванов, Базы данных, 4>; <Иванов, Базы данных, 5>; <Крылов, Базы данных, 3>; <Крылов, Базы данных, 4>; <Крылов, Базы данных, 5>; <Степанов, Базы данных, 3>; <Степанов, Базы данных, 4>; <Степанов, Базы данных, 5>; Отношение R моделирует реальную ситуацию и оно может содержать, допустим, только 5 строк, которые соответствуют результатам сессии (Крылов экзамен по "Базам данных" еще не сдавал): <Иванов, Теория автоматов, 4>; <Крылов, Теория автоматов, 5>; <Степанов, Теория автоматов, 5>; <Иванов, Базы данных, 3>; <Степанов, Базы данных, 4>;

Отношения Схемой отношения R называется перечень имен атрибутов данного отношения с указанием домена, к которому они относятся: Если атрибуты принимают значения из одного и того же домена, то они называются θ сравнимыми, где θ — множество допустимых операций сравнения, заданных для данного домена. Например, если домен содержит числовые данные, то для него допустимы все операции сравнения, тогда θ = { =, <>, >=, <=, >, <}. Если для домена, содержащего символьные данные, задано лексикографическое упорядочение, то он имеет также полный спектр операций сравнения.

Отношения Схемы двух отношений называются эквивалентными, если они имеют одинаковую степень и возможно такое упорядочение имен атрибутов в схемах, что на одинаковых местах будут находиться сравнимые атрибуты, то есть атрибуты, принимающие значения из одного домена. SR 1 = (A 1, A 2, . . . , An) — схема отношения R 1. SR 2 = (Bi 1, Bi 2, . . . , Bin) — схема отношения R 2 после упорядочения имен атрибутов. Тогда: 1. n = m, SR 1 ~ SR 2 2. Aj , Bij Dj Для поддержки связей в отношениях существуют первичный ключ (PRIMARY KEY), который однозначно определяет кортеж основного отношения, и внешний ключ (FOREIGN KEY), определяющий множество кортежей подчинённого отношения, которые связаны с единственным кортежем основного отношения.
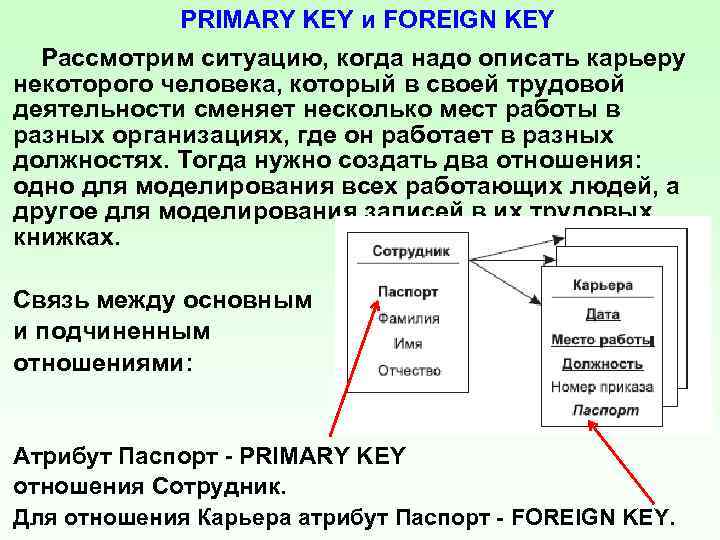
PRIMARY KEY и FOREIGN KEY Рассмотрим ситуацию, когда надо описать карьеру некоторого человека, который в своей трудовой деятельности сменяет несколько мест работы в разных организациях, где он работает в разных должностях. Тогда нужно создать два отношения: одно для моделирования всех работающих людей, а другое для моделирования записей в их трудовых книжках. Связь между основным и подчиненным отношениями: Атрибут Паспорт PRIMARY KEY отношения Сотрудник. Для отношения Карьера атрибут Паспорт FOREIGN KEY.

Данные в таблицах удовлетворяют следующим принципам: 1. Каждое значение, содержащееся на пересечении строки и столбца, должно быть атомарным. 2. Значения данных в одном и том же столбце должны принадлежать к одному и тому же типу, доступному для использования в данной СУБД. 3. Каждая запись в таблице уникальна, то есть в таблице не существует двух записей с полностью совпадающим набором значений ее полей. 4. Каждое поле имеет уникальное имя. 5. Последовательность полей в таблице несущественна. 6. Последовательность записей в таблице несущественна.

Реляционная модель данных Достоинство реляционной модели данных заключается в простоте, понятности и удобстве физической реализации на ЭВМ. Именно простота и понятность для пользователя явились основной причиной ее широкого использования. К основным недостаткам реляционной модели относятся отсутствие стандартных средств идентификации отдельных записей и сложность описания не иерархических и сетевых связей. Примерами зарубежных реляционных СУБД для ПЭВМ являются: MS SQL Server, Oracle, DB 2, Paradox, Fox. Pro, Access, Clarion, Ingres. К отечественным СУБД реляционного типа относятся системы ПАЛЬМА и Hy. Tech.

Операции над отношениями. Реляционная алгебра Алгеброй называется множество объектов с заданной на нем совокупностью операций, замкнутых относительно этого множества, называемого основным множеством. Основным множеством в реляционной алгебре является множество отношений. Всего Э. Ф. Коддом было предложено 8 операций. Все множество операций можно разделить на две группы: 1. теоретико-множественные операции: Ø Объединение Ø Пересечение бинарные операции Ø Разность Ø Расширенное декартово произведение. 2. специальные операции: Ø Горизонтальный выбор или операция фильтрации Ø Вертикальный выбор или операция проектирования Ø Операция условного соединения Ø Операция деления.

Теоретико множественные операции Пусть заданы два отношения R 1 = { r 1 } , R 2 = { r 2 }, где r 1 и r 2 соответственно кортежи отношений R 1 и R 2. Ø Объединением (Union) двух отношений называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно: R 1 R 2 = { r | r R 1 ⋁ r R 2 }, здесь r — кортеж нового отношения, ⋁ операция логического сложения «ИЛИ» . Ø Пересечением (Intersect) отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям R 1 и R 2: R 3 = R 1 R 2 ={ r | r R 1 ⋀ r R 2 }, здесь ⋀ операция логического умножения «И» .

Теоретико множественные операции Ø Разностью отношений (Minus) R 1 и R 2 называется отношение, содержащее множество кортежей, принадлежащих R 1 и не принадлежащих R 2 и наоборот: R 4 = R 1 R 2 = { r | r R 1 ⋀ r R 2 }, R 5 = R 2 R 1 = { r | r R 2 ⋀ r R 1 }. Операции объединение и пересечение явля ются коммутативными операциями, то есть результат операции не зависит от порядка аргументов в операции. Операция разности – несимметричная операцией. Операции объединения, пересечения и разности применимы только к отношениям с эквивалентными схемами. Ø Расширенное декартово произведение (Times). Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, => операция R 1 ⊗ R 2 допустима для любых двух отношений.

Теоретико множественные операции Введем дополнительно понятие: cцеплением или конкатенацией кортежей с = <c 1, c 2, . . . , сn> и q = <q 1, q 2 … qm> называется кортеж, полученный добавлением значений второго в конец первого. Сцепление кортежей с и q обозначается как (с , q): (с, q) = < c 1, c 2, . . . , сn, q 1, q 2 … qm >. Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q. Операция декартова произведения меняет степень результирующего отношения.

Теоретико множественные операции Ø Расширенным декартовым произведением отношения R 1 степени n, со схемой SR 1 = (A 1, А 2, …, Аn) и отношения R 2 степени m, со схемой SR 2 = (B 1, B 2 , …, Bm) называется отношение R 3 степени n+m со схемой SR 3 = (A 1, А 2, …, Аn, B 1, B 2 , …, Bm), содержащее кортежи, полученные сцеплением каждого кортежа r отношения R 1 с каждым кортежем q отношения R 2. То есть, если R 1= { r }, R 2 = { q }, то R 1 ⊗ R 2 = {(r, q) | r R 1 ⋀ q R 2 } Операцию декартова произведения с учетом возможности перестановки атрибутов в отношении можно считать симметричной.

Специальные операции реляционной алгебры Ø Операция выбора (Select) или операция фильтрации – это унарная операция над отношением с использованием предикатов. Операция, задана на отношении R в виде булевского выражения, определенного на атрибутах отношения R. Результат операции – это отношение R[α(r)] , включающее те кортежи из исходного отношения, для которых истинно условие выбора: R[α(r)] = {r | r R ⋀ α(r) = “Истина”} Например: R 2 = R [ Вес детали < 140]
![Специальные операции реляционной алгебры Ø Операция проектирования (Project) или вертикального выбора называется отношение R[B] Специальные операции реляционной алгебры Ø Операция проектирования (Project) или вертикального выбора называется отношение R[B]](https://present5.com/presentation/3/25175739_141789796.pdf-img/25175739_141789796.pdf-16.jpg)
Специальные операции реляционной алгебры Ø Операция проектирования (Project) или вертикального выбора называется отношение R[B] со схемой, соответствующей набору атрибутов B, содержащему кортежи, полученные из кортежей исходного отношения R путем удаления из них значений, не принадлежащих атрибутам из набора B. Это также унарная операция над отношением. Но если операция выбора выбирает подмножество строк в отношении, то операция проекции выбирает подмножество столбцов. Ø Операция соединения (Join) является бинарной, исходными для нее являются два отношения, а результатом одно. Т. е. соединение является комбинацией двух отношений, имеющих общее значение для одного или нескольких общих атрибутов этих двух отношений.
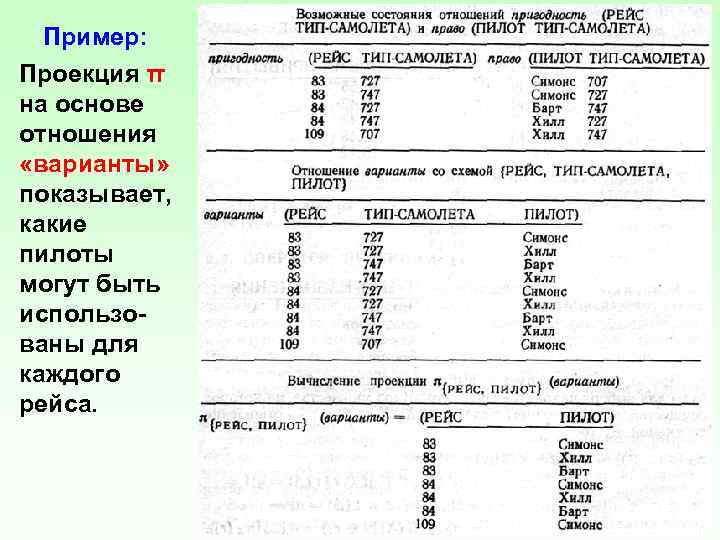
Пример: Проекция π на основе отношения «варианты» показывает, какие пилоты могут быть использо ваны для каждого рейса.
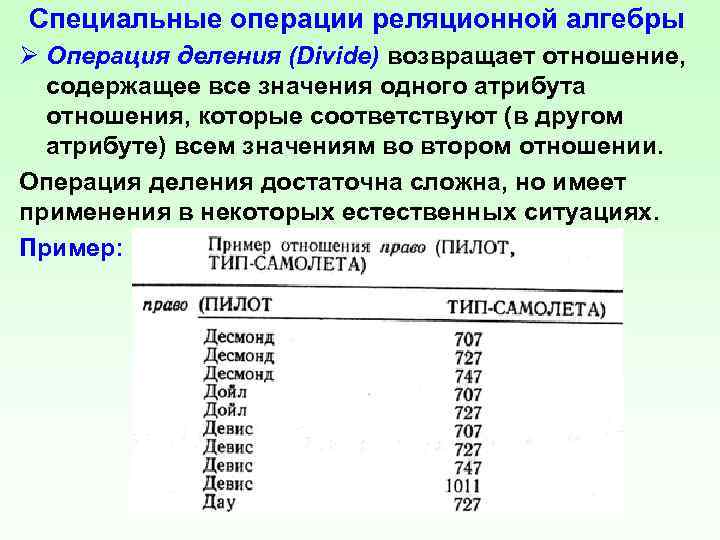
Специальные операции реляционной алгебры Ø Операция деления (Divide) возвращает отношение, содержащее все значения одного атрибута отношения, которые соответствуют (в другом атрибуте) всем значениям во втором отношении. Операция деления достаточна сложна, но имеет применения в некоторых естественных ситуациях. Пример:

Операция деления Предположим, что требуется найти тех пилотов, которые имеют право управлять всеми типами самолётов из некоторого множества. Пусть q(ТИП САМОЛЁТА) и s(ТИП САМОЛЁТА) следующие: Деление может использоваться для сбора информации о пилотах, имеющих право управлять самолётами из множеств q или s.
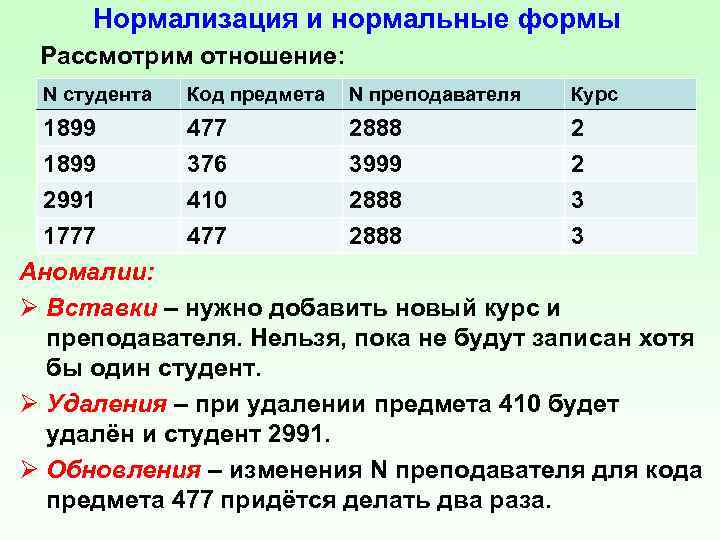
Нормализация и нормальные формы Рассмотрим отношение: N студента Код предмета N преподавателя Курс 1899 477 2888 2 1899 376 3999 2 2991 410 2888 3 1777 477 2888 3 Аномалии: Ø Вставки – нужно добавить новый курс и преподавателя. Нельзя, пока не будут записан хотя бы один студент. Ø Удаления – при удалении предмета 410 будет удалён и студент 2991. Ø Обновления – изменения N преподавателя для кода предмета 477 придётся делать два раза.

Нормализация – это процесс создания отношений, в которых отсутствуют недостатки плохой реляционной структуры. Для достижения нормализации есть два способа: Ø Первый — начать работу с ER диаграммы. Если диаграмма построена правильно, можно с помощью нескольких простых правил преобразовать ее в отношения, избежав при этом большинства проблем, свойственных реляционному проектированию. Недостатком такого подхода является возможная трудность определения правильности структуры. Ø Второй — воспользоваться для создания отношений теоретическими концепциями построения корректного проекта. Это несколько сложнее, чем работа с ER диаграммой, но часто приводит к разработке лучшей структуры. На практике может оказаться полезным использование комбинации обоих подходов.

Нормальные формы Теоретические правила, которым отвечает структура отношения, называются нормальными формами (normal forms). С возрастанием порядкового номера нормальной формы набор правил постоянно усложняется. В теории, чем выше номер нормальной формы, тем лучше структура отношения. В теории реляционных БД обычно выделяется следующая последовательность нормальных форм: Ø первая нормальная форма (1 NF); Ø вторая нормальная форма (2 NF); Ø третья нормальная форма (3 NF); Ø нормальная форма Бойса Кодда (BCNF); Ø четвертая нормальная форма (4 NF); Ø пятая нормальная форма, или нормальная форма проекции соединения (5 NF или PJ/NF).

Нормальные формы В большинстве случаев, если можно установить соответствие отношений третьей нормальной форме (3 NF), удастся избежать многих проблем, присущих плохим реляционным проектам. Нормальная форма Бойса Кодда (BCNF) и 4 NF используются в особых ситуациях. 5 NF очень сложна и, как правило, используется очень редко. 1. Каждая следующая нормальная форма в некотором смысле лучше предыдущей; 2. При переходе к следующей NF свойства предыдущих нормальных форм сохраняются. Метод нормализации заключается в декомпозиции отношения, находящегося в предыдущей NF, в два или более отношения, удовлетворяющих требованиям следующей NF.

Функциональная и транзитивная зависимости Функциональная зависимость – в отношении R атрибут Y функционально зависит от атрибута Х в том и только в том случае, если каждому значению Х соответствует в точности одно значение Y: R. Х R. Y Полная функциональная зависимость – функциональная зависимость R. Х R. Y называется полной, если атрибут Y не зависит функционально от любого точного подмножества Х (точным подмножеством множества Х называется любое его подмножество, не совпадающее с X). Транзитивная зависимость – зависимость R. Х R. Y называется транзитивной, если существует такой атрибут Z, что имеются функциональные зависимости R. Х R. Z и R. Z R. Y и отсутствует функциональная зависимость R. Z R. X.

1 NF Все атрибуты отношения простые (далее неделимые), т. е. все строки содержат не более одного значения в каждом столбце. 2 NF Отношение R находится во второй нормальной форме (2 NF) в том и только в том случае, когда оно находится в 1 NF, и каждый неключевой атрибут полностью зависит от первичного ключа. Нарушения 2 NF (на примере отношения Снабжение): 1. Не можем ввести сведения о поставщике, пока он не поставит некоторое изделие. 2. Удаление записи с N поставщика приведёт к удалению всех сведений о нём. 3. При изменении сведений о поставщике, необходимо проверить каждую запись на содержание в ней ключа этого поставщика.
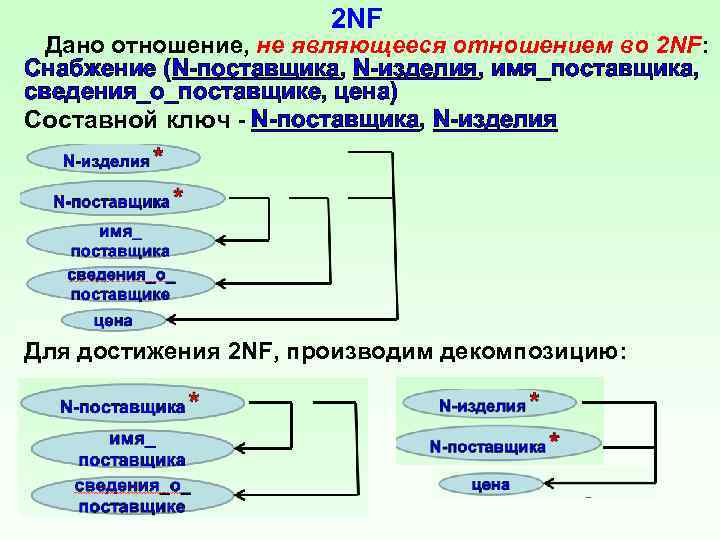
2 NF Дано отношение, не являющееся отношением во 2 NF: Снабжение (N поставщика, N изделия, имя_поставщика, сведения_о_поставщике, цена) Составной ключ N поставщика, N изделия Для достижения 2 NF, производим декомпозицию:

3 NF Отношение R находится в третьей нормальной форме (3 NF) в том и только в том случае, когда оно находится во 2 NF, и каждый неключевой атрибут зависит только от первичного ключа, т. е. исключаются транзитивные зависимости. Нарушения 3 NF (на примере отношения Служащий): 1. До привлечения конкретного служащего к работе, дату окончания проекта некуда было записывать. 2. Если бы вдруг все служащие прекратили работу над данным проектом и были бы удалены из БД, тогда в БД были бы уничтожены все сведения о дате окончания проекта. 3. Изменение даты окончания проекта приводит к необходимости поиска всех записей, содержащих эту дату, и их модификации.
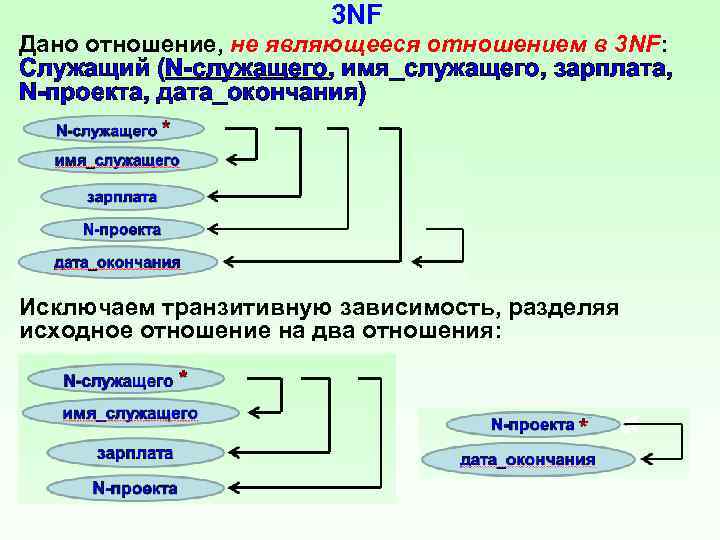
3 NF Дано отношение, не являющееся отношением в 3 NF: Служащий (N служащего, имя_служащего, зарплата, N проекта, дата_окончания) Исключаем транзитивную зависимость, разделяя исходное отношение на два отношения:

BCNF (форма Бойса Кодда) Форма Бойса Кодда улучшает 3 NF, исключая ситуации, которые возникают при наличии нескольких возможных ключей с перекрывающимися компонентами. BCNF требует разделения избыточных ключей. Нормальные отношения высших порядков уже связаны не с функциональными зависимостями, а отражают более тонкие вопросы предметной области. Реляционная база данных эффективна, если все ее отношения находятся как минимум в 3 NF, а предпочтительнее — в BCNF.
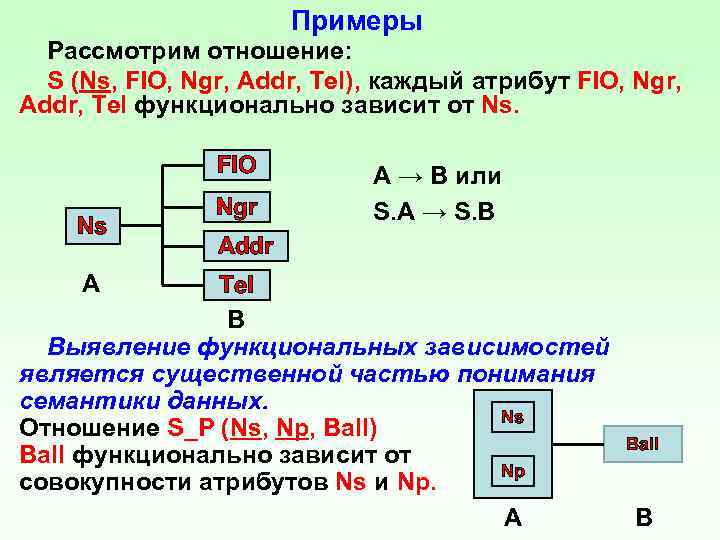
Примеры Рассмотрим отношение: S (Ns, FIO, Ngr, Addr, Tel), каждый атрибут FIO, Ngr, Addr, Tel функционально зависит от Ns. FIO A → B или Ngr S. A → S. B Ns Addr A Tel B Выявление функциональных зависимостей является существенной частью понимания семантики данных. Ns Отношение S_P (Ns, Np, Ball) Ball функционально зависит от Nр совокупности атрибутов Ns и Np. А В

Отношение STUD (Ns, FIO, Ngr, Addr, Tel, Np, Ball) находится в 1 NF. Ключ составной (Ns, Np). Атрибуты FIO, Ngr, Addr, Tel не находятся в полной функциональной зависимости от ключа (Ns, Np), они функционально зависят от части ключа. Преобразуем STUD в два отношения: S (Ns, FIO, Ngr, Addr, Tel) S_P (Ns, Np, Ball) Отношение SS (Ns, FIO, Ngr, Spec, Addr, Tel) Spec – специальность, которая определяется конкретной группой. Spec транзитивно зависит от Ns, информация о специальности будет храниться только тогда, когда в группе будет хотя бы один студент. Кроме того, специальность дублируется для всех студентов в группе. Ns Ngr, Ngr Spec, Spec транзитивно зависит от Ns. S (Ns, FIO, Ngr, Addr, Tel) Spec_S (Ngr, Spec)

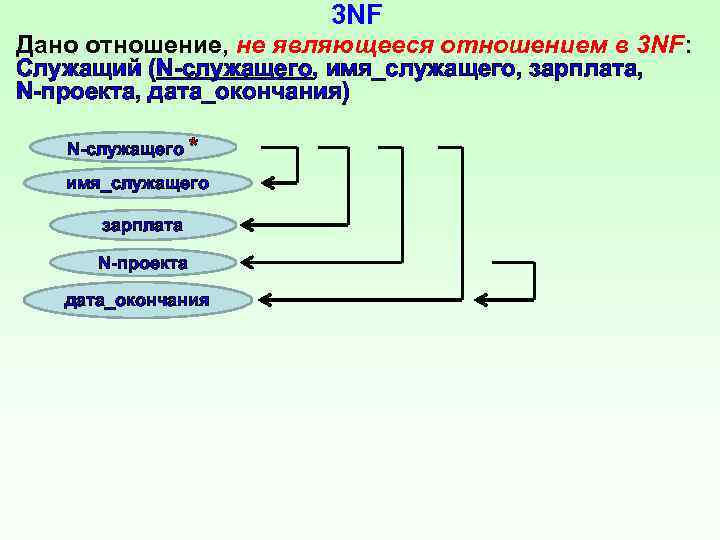
3 NF Дано отношение, не являющееся отношением в 3 NF: Служащий (N служащего, имя_служащего, зарплата, N проекта, дата_окончания) N служащего * имя_служащего зарплата N проекта дата_окончания
Л5_Реляционная модель_Нормализация.ppt