Раздел 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ТЕМА 4. ПРЕДЕЛЫ Лекция









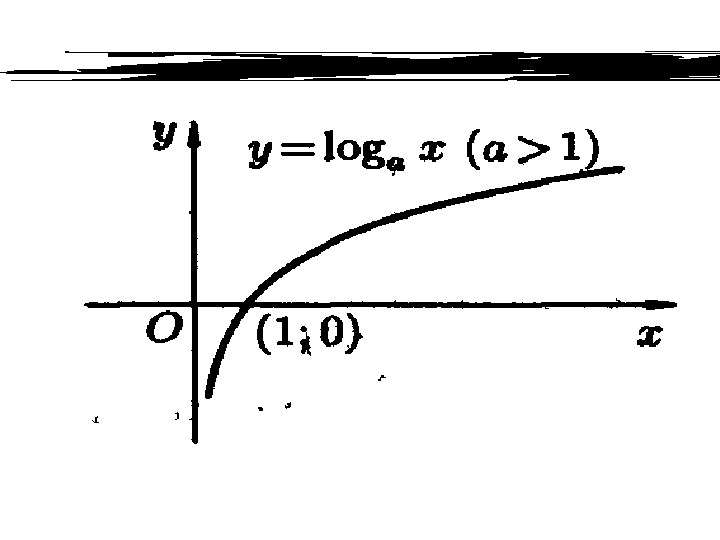











4.1_09g_2011.ppt
- Размер: 309.5 Кб
- Автор:
- Количество слайдов: 24
Описание презентации Раздел 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ТЕМА 4. ПРЕДЕЛЫ Лекция по слайдам
 Раздел 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ТЕМА 4. ПРЕДЕЛЫ Лекция 4. 1. Функция. Числовая последовательность. Вопросы 1. Функция. 2. Основные элементарные функции и их графики. 3. Числовая последовательность и ее предел. 4. Свойства пределов последовательностей.
Раздел 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ТЕМА 4. ПРЕДЕЛЫ Лекция 4. 1. Функция. Числовая последовательность. Вопросы 1. Функция. 2. Основные элементарные функции и их графики. 3. Числовая последовательность и ее предел. 4. Свойства пределов последовательностей.
 1. Функция Опр. Заданы два непустых множества Х и Y. Соответствие , которое каждому элементу х Х сопоставляет один и только один элемент у Y , называется функцией и записывается у = f (х), х Х или f: Х Y.
1. Функция Опр. Заданы два непустых множества Х и Y. Соответствие , которое каждому элементу х Х сопоставляет один и только один элемент у Y , называется функцией и записывается у = f (х), х Х или f: Х Y.
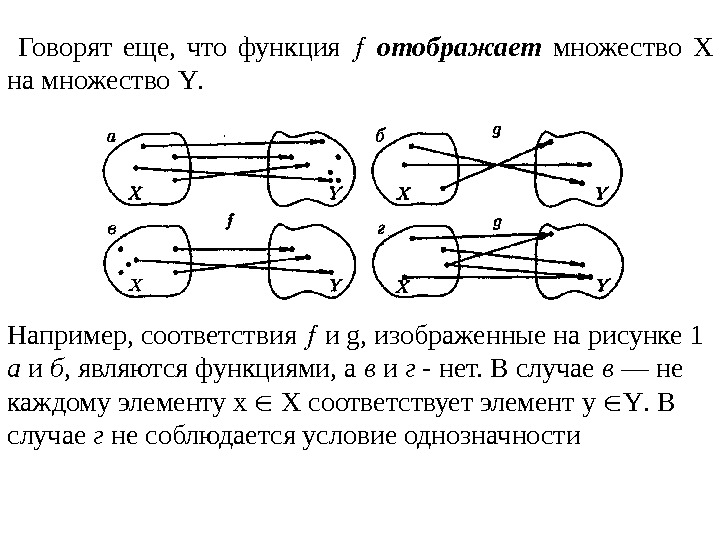
 Говорят еще, что функция отображает множество Х на множество Y. Например, соответствия и g , изображенные на рисунке 1 а и б , являются функциями, а в и г — нет. В случае в — не каждому элементу х Х соответствует элемент у Y. В случае г не соблюдается условие однозначности
Говорят еще, что функция отображает множество Х на множество Y. Например, соответствия и g , изображенные на рисунке 1 а и б , являются функциями, а в и г — нет. В случае в — не каждому элементу х Х соответствует элемент у Y. В случае г не соблюдается условие однозначности
 Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х ). Относительно самих величин x и у говорят, что они находятся в функциональной зависимости. у = у(х) или у = f (х) Частное значение функции f (х) при х = а записывают так: (а). Например, если f (х) = 2 x 2 — 3, то (0) = -3, (2) =5.
Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х ). Относительно самих величин x и у говорят, что они находятся в функциональной зависимости. у = у(х) или у = f (х) Частное значение функции f (х) при х = а записывают так: (а). Например, если f (х) = 2 x 2 — 3, то (0) = -3, (2) =5.
 Опр. Графиком функции у = f (х) называется множество всех точек плоскости Оху, для каждой из которых х является значением аргумента, a y — соответствующим значением функции.
Опр. Графиком функции у = f (х) называется множество всех точек плоскости Оху, для каждой из которых х является значением аргумента, a y — соответствующим значением функции.
 Т ри способа задания функции: аналитический, табличный, графический. Аналитический способ: функция задается в виде одной или нескольких формул или уравнений Графический способ: задается график функции. Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции.
Т ри способа задания функции: аналитический, табличный, графический. Аналитический способ: функция задается в виде одной или нескольких формул или уравнений Графический способ: задается график функции. Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции.
 Основные характеристики функции 1. Функция у = f (х), определенная на множестве D, называется четной, если х D выполняются условия -х D и f (-х) = f (х); нечетной, если х D выполняются условия -х D и f ( — х) = — f (х). График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.
Основные характеристики функции 1. Функция у = f (х), определенная на множестве D, называется четной, если х D выполняются условия -х D и f (-х) = f (х); нечетной, если х D выполняются условия -х D и f ( — х) = — f (х). График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.
 2. Пусть функция y = f ( x ) определена на множестве D. Если для ( х 1 , х 2 ) D из х 1 < х 2 f ( x 1 ) < f ( x 2 ), то ф-я наз возрастающей на множестве D ; из х 1 < х 2 f ( x 1 ) (х 2 ) , то ф-я наз неубывающей ; из х 1 f ( x 2 ), то ф-я наз убывающей; из х 1 < х 2 f ( x 1 ) ( x 2 ) , то ф-я наз невозрастающей . Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными.
2. Пусть функция y = f ( x ) определена на множестве D. Если для ( х 1 , х 2 ) D из х 1 < х 2 f ( x 1 ) < f ( x 2 ), то ф-я наз возрастающей на множестве D ; из х 1 < х 2 f ( x 1 ) (х 2 ) , то ф-я наз неубывающей ; из х 1 f ( x 2 ), то ф-я наз убывающей; из х 1 < х 2 f ( x 1 ) ( x 2 ) , то ф-я наз невозрастающей . Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве D называются монотонными на этом множестве, а возрастающие и убывающие — строго монотонными.
 3. Функцию у = f (х), х D, называется ограниченной на D, если М >0: x D f (х) М. Отсюда следует, что график ограниченной функции лежит между прямыми у = -М и у = М (см. рис. ). · 4. Функция у = f (х), определенная на D, называется периодической на этом множестве, если Т > O, что при каждом х D значение (х+ T) D и f (х+ T) = f (х). При этом число T называется периодом функции.
3. Функцию у = f (х), х D, называется ограниченной на D, если М >0: x D f (х) М. Отсюда следует, что график ограниченной функции лежит между прямыми у = -М и у = М (см. рис. ). · 4. Функция у = f (х), определенная на D, называется периодической на этом множестве, если Т > O, что при каждом х D значение (х+ T) D и f (х+ T) = f (х). При этом число T называется периодом функции.
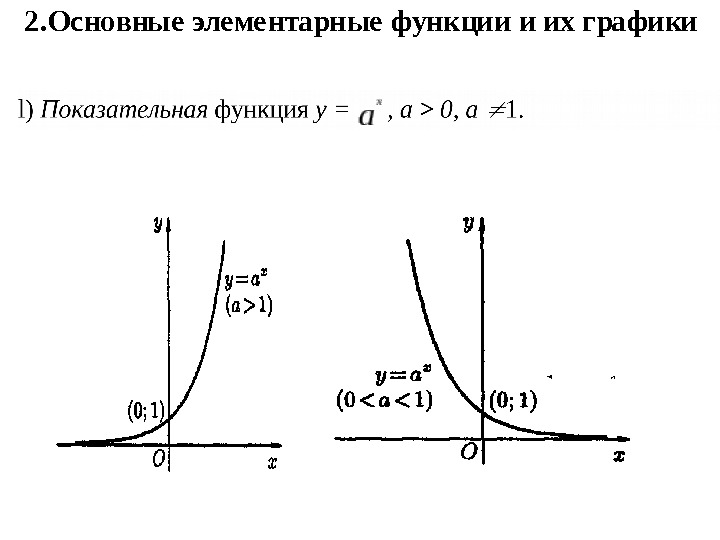
 2. Основные элементарные функции и их графики
2. Основные элементарные функции и их графики
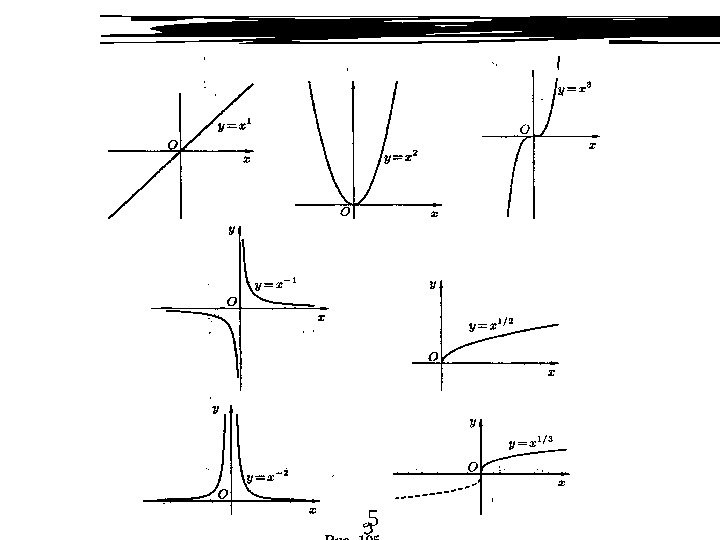
 52) Степенная функция у = х R.
52) Степенная функция у = х R.
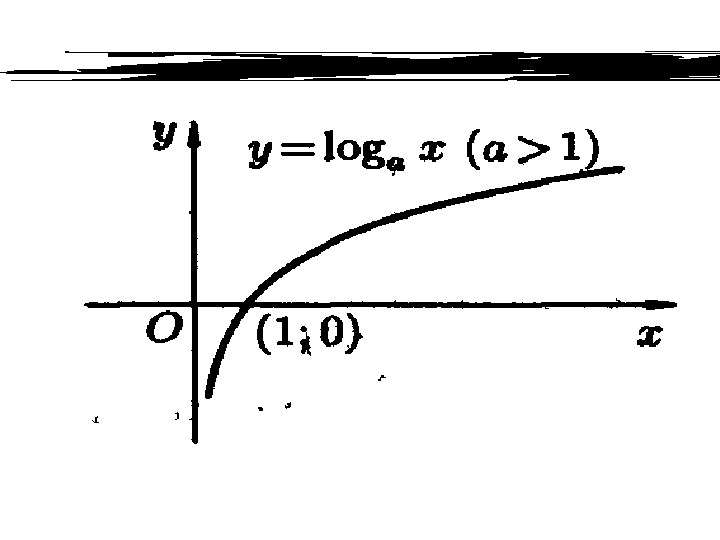 3) Логарифмическая функция у = logаx, а > 0, а 1;
3) Логарифмическая функция у = logаx, а > 0, а 1;
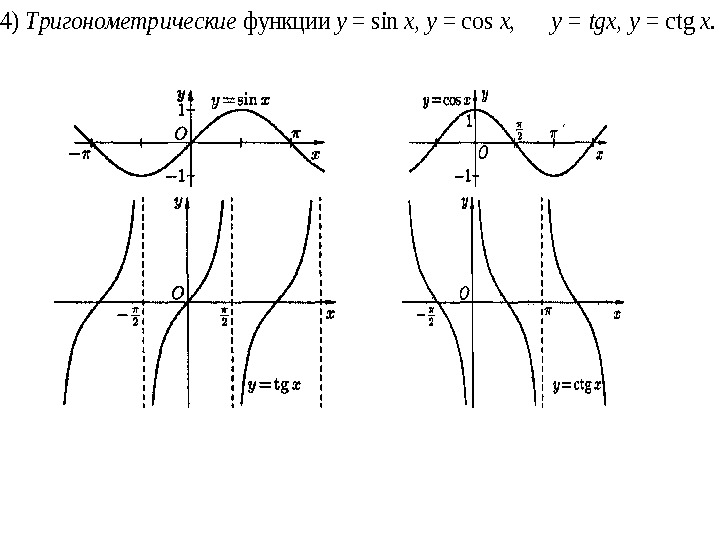
 4) Тригонометрические функции у = sin х, у = cos х, у = tgx, у = ctg х.
4) Тригонометрические функции у = sin х, у = cos х, у = tgx, у = ctg х.
 заданная на множестве N натуральных чисел. def: { x n } или x п , n N. Число х 1 называется первым членом (элементом) последовательности, x 2 — вторым, . . . , x п — общим или п-м членом последовательности. Опр. Под числовой последовательностью х 1 , х 2 , х з , … , x п , … понимается функция х п = f (n) , 3. Числовая последовательность и ее предел
заданная на множестве N натуральных чисел. def: { x n } или x п , n N. Число х 1 называется первым членом (элементом) последовательности, x 2 — вторым, . . . , x п — общим или п-м членом последовательности. Опр. Под числовой последовательностью х 1 , х 2 , х з , … , x п , … понимается функция х п = f (n) , 3. Числовая последовательность и ее предел
 n = n ² + 1, z n = , y n = , u n = , n N задают соответственно последовательности nn 1 n 1 n n 1 n ={2, 5, 10, . . . , n ² + 1, . . . }; z n ={-1, 2, -3, 4, . . . , , . . . }; у n ={1, , …, , …} u n ={0, , , …, , …} nn
n = n ² + 1, z n = , y n = , u n = , n N задают соответственно последовательности nn 1 n 1 n n 1 n ={2, 5, 10, . . . , n ² + 1, . . . }; z n ={-1, 2, -3, 4, . . . , , . . . }; у n ={1, , …, , …} u n ={0, , , …, , …} nn
 Опр. Последовательность {хn} называется ограниченной, если М > О т. ч. n N выполняется неравенство хn М. Опр. Последовательность {хn} называется возрастающей (неубывающей), если для т выполняется неравенство am+1 > am (am+1 am).
Опр. Последовательность {хn} называется ограниченной, если М > О т. ч. n N выполняется неравенство хn М. Опр. Последовательность {хn} называется возрастающей (неубывающей), если для т выполняется неравенство am+1 > am (am+1 am).
 Опр. Число а называется пределом последовательности {х n }, если для любого положительного числа найдется такое натуральное число N, что при всех n > N выполняется неравенство x n — a < .
Опр. Число а называется пределом последовательности {х n }, если для любого положительного числа найдется такое натуральное число N, что при всех n > N выполняется неравенство x n — a < .
 Коротко определение предела можно записать так: ( 0 N : n N x n – a ) lim x n = a
Коротко определение предела можно записать так: ( 0 N : n N x n – a ) lim x n = a
 Пример Доказать, что 11 lim nn n. Решение: По определению, число 1 будет пределом последовательности x n = , n N, если > 0 найдется натуральное число N, такое, что для всех n > N выполняется неравенство -1 , т. е. . Оно справедливо для всех n > , т. е. для всех n > N = [ ] , где [ ] — целая часть числа (целая часть числа х, обозначаемая [ х ] , есть наибольшее целое число, не превосходящее х; так [3] = 3, [5, 2] = 5). Если > l, то в качестве N можно взять [ ] + 1. Итак, > 0 указано соответствующее значение N. Это и доказывает, что п п 1 1 1 п п 1 11 lim nn n
Пример Доказать, что 11 lim nn n. Решение: По определению, число 1 будет пределом последовательности x n = , n N, если > 0 найдется натуральное число N, такое, что для всех n > N выполняется неравенство -1 , т. е. . Оно справедливо для всех n > , т. е. для всех n > N = [ ] , где [ ] — целая часть числа (целая часть числа х, обозначаемая [ х ] , есть наибольшее целое число, не превосходящее х; так [3] = 3, [5, 2] = 5). Если > l, то в качестве N можно взять [ ] + 1. Итак, > 0 указано соответствующее значение N. Это и доказывает, что п п 1 1 1 п п 1 11 lim nn n
 Выясним геометрический смысл определения предела последователь ности. Неравенство (2) равносильно неравенствам — < x – a < или а- < x n N, попадут в -окрестность точки а (см. рис. ). Чем меньше , тем больше число N, но в любом случае внутри — окрестности точки а находится бесконечное число членов после- довательности, а вне ее может быть лишь конечное их число.
Выясним геометрический смысл определения предела последователь ности. Неравенство (2) равносильно неравенствам — < x – a < или а- < x n N, попадут в -окрестность точки а (см. рис. ). Чем меньше , тем больше число N, но в любом случае внутри — окрестности точки а находится бесконечное число членов после- довательности, а вне ее может быть лишь конечное их число.
 Отсюда следует, что сходящаяся последоват ельност ь имеет только один предел. Последовательность, не имеющая предела, назы- вается расходящейся.
Отсюда следует, что сходящаяся последоват ельност ь имеет только один предел. Последовательность, не имеющая предела, назы- вается расходящейся.
 Теорема: Р азность сходящихся последов ательностей {xn} и {yn} есть сходящаяся последовательность, пред ел которой равен разно сти пред елов последовательностей {xn} и {yn}. Теорема: Про изведение сходящихся последователь ностей { x n } и { y n } есть сходящаяся последовательность, пред ел которой равен произв едению пределов последовательностей { x n } и { y n }. Теорема: Ч астное сходящихся по следовательно стей { x n } и { y n }, при условии что предел { y n } отличен от нуля , есть сходящая ся последовательность, предел кото рой рав ен частно му пред елов последователь ностей { x n } и { y n }. Теорема: Сумма сходящихся последовательностей {xn} и {yn} есть сходящаяся последователь ность, предел которой равен сумме пределов последовательностей {xn} и {yn}.
Теорема: Р азность сходящихся последов ательностей {xn} и {yn} есть сходящаяся последовательность, пред ел которой равен разно сти пред елов последовательностей {xn} и {yn}. Теорема: Про изведение сходящихся последователь ностей { x n } и { y n } есть сходящаяся последовательность, пред ел которой равен произв едению пределов последовательностей { x n } и { y n }. Теорема: Ч астное сходящихся по следовательно стей { x n } и { y n }, при условии что предел { y n } отличен от нуля , есть сходящая ся последовательность, предел кото рой рав ен частно му пред елов последователь ностей { x n } и { y n }. Теорема: Сумма сходящихся последовательностей {xn} и {yn} есть сходящаяся последователь ность, предел которой равен сумме пределов последовательностей {xn} и {yn}.
 Теорема Если x n = а, y n = b и, начиная с некоторого номера, выполняется неравенство x n y n , то а b. lim n
Теорема Если x n = а, y n = b и, начиная с некоторого номера, выполняется неравенство x n y n , то а b. lim n
 Теорема (Вейерштрасс). Всякая монотонная ограниченная последовательность имеет предел
Теорема (Вейерштрасс). Всякая монотонная ограниченная последовательность имеет предел

