Расчет переходного процесса в схемах с сосредоточенными параметрами

Расчет переходного процесса в схемах с сосредоточенными параметрами Схемы 1 и 2 порядков

преобразование Лапласа л1 Сумма функций – 2. Теорема подобия – 3. Первая теорема смещения – 4. Теорема затухания – 5. Теорема дифференциро- вания для оригинала – 6. Теорема интегрирования для оригинала – 7. Теорема свертывания (произведение изображений) – 8. Теорема разложения – q – степень полинома в знаменателе, – корни полинома в знаменателе. 2

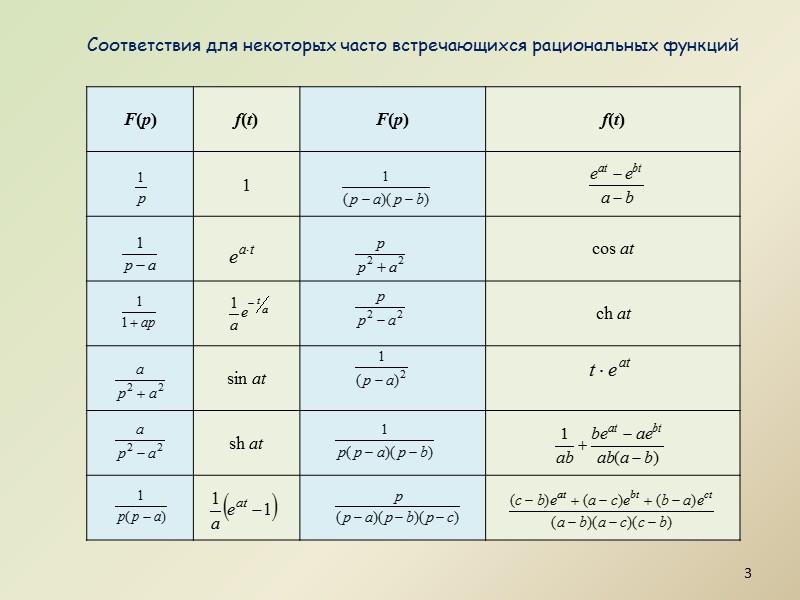
Соответствия для некоторых часто встречающихся рациональных функций 3

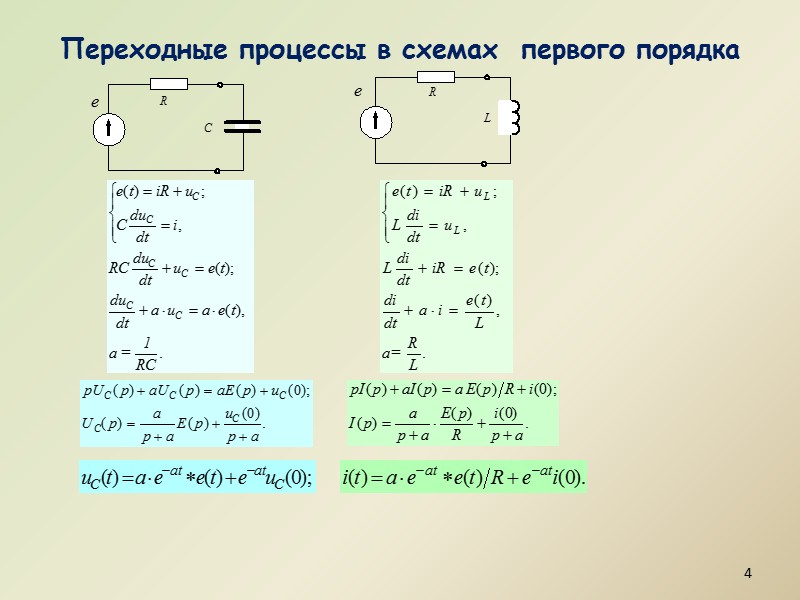
Переходные процессы в схемах первого порядка 4

Решение при постоянном воздействии 5 Аналитика для спадающей экспоненты Приближенное решение

Решение для затухающей синусоиды 6

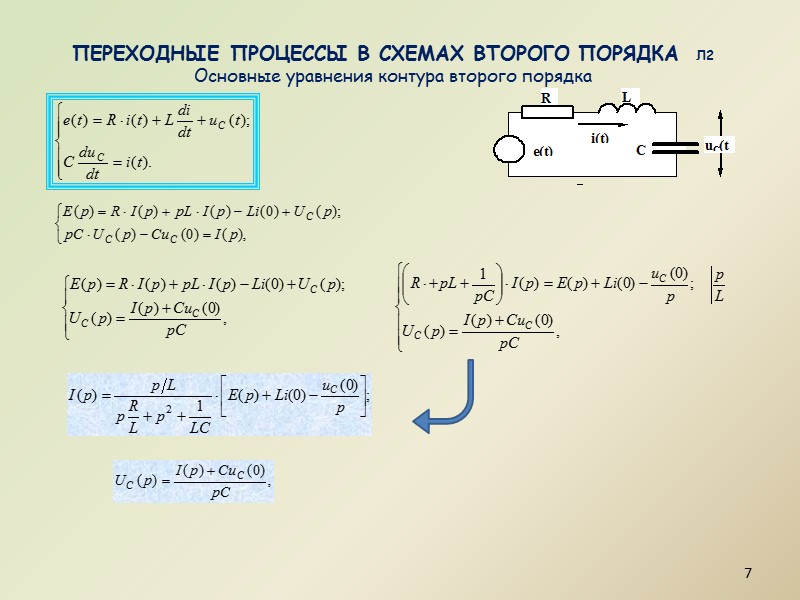
Переходные процессы в схемах второго порядка л2 Основные уравнения контура второго порядка 7

Включение контура второго порядка на постоянную ЭДС 8 Оригинал решения будет зависеть от вида корней полинома относительно p в знаменателе 1.  корни вещественные кратные:

9 2.  корни вещественные различные:

10 3.  корни комплексные сопряженные :

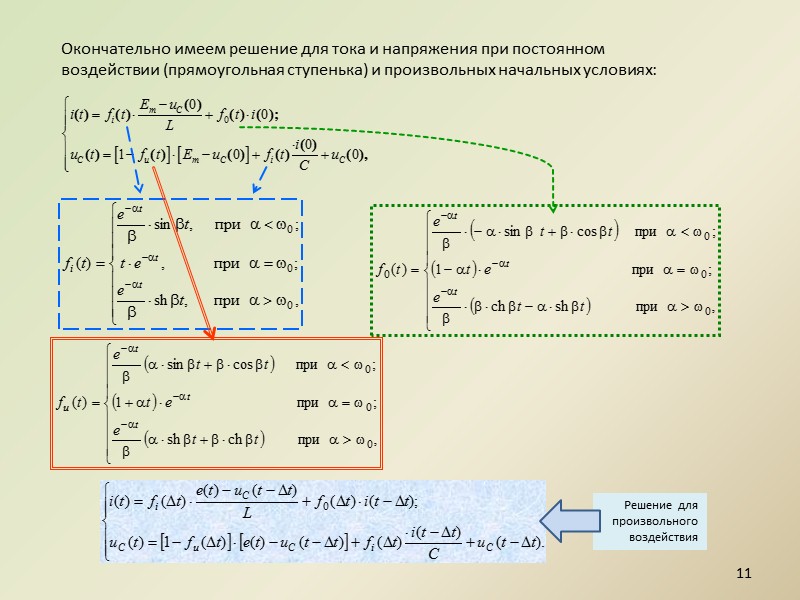
11 Окончательно имеем решение для тока и напряжения при постоянном воздействии (прямоугольная ступенька) и произвольных начальных условиях: Решение для произвольного воздействия

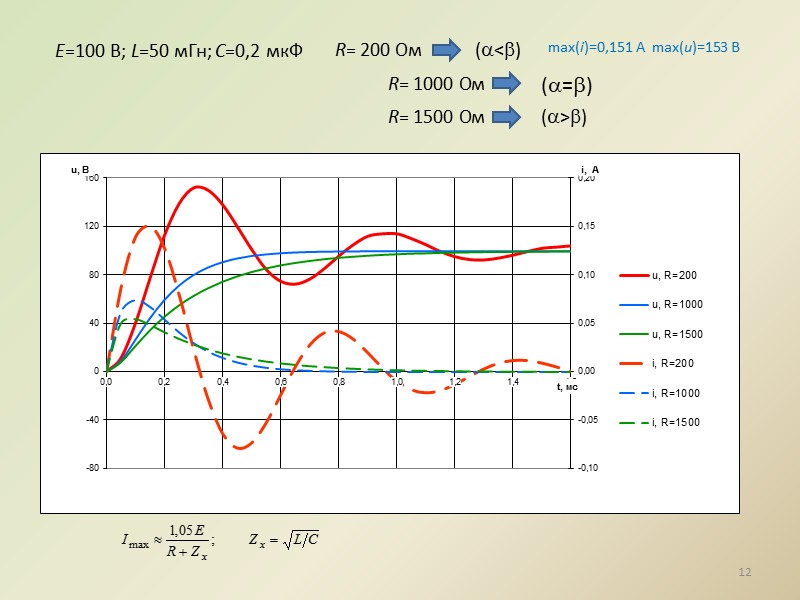
E=100 В; L=50 мГн; С=0,2 мкФ 12 R= 200 Ом (<) R= 1000 Ом (=) R= 1500 Ом (>) max(i)=0,151 А max(u)=153 В

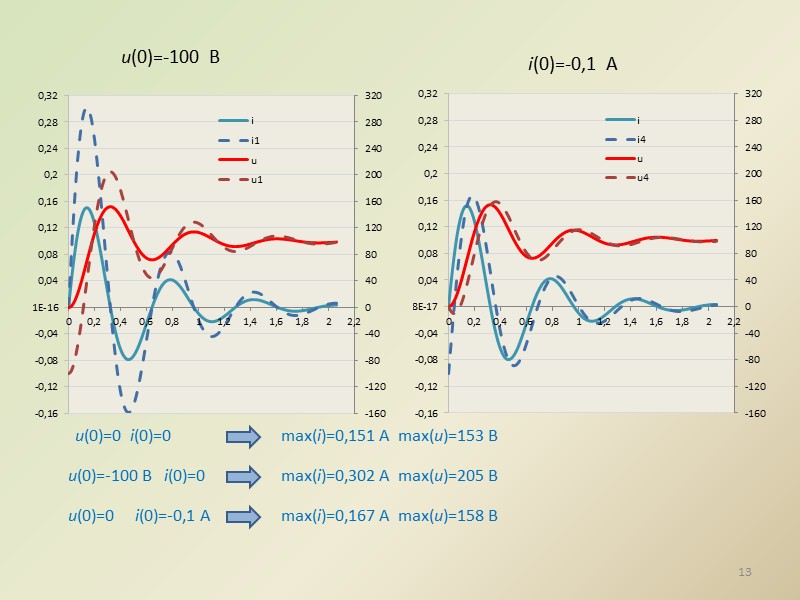
13 u(0)=-100 В i(0)=-0,1 A max(i)=0,151 А max(u)=153 В u(0)=0 i(0)=0 u(0)=-100 B i(0)=0 max(i)=0,302 А max(u)=205 В u(0)=0 i(0)=-0,1 A max(i)=0,167 А max(u)=158 В

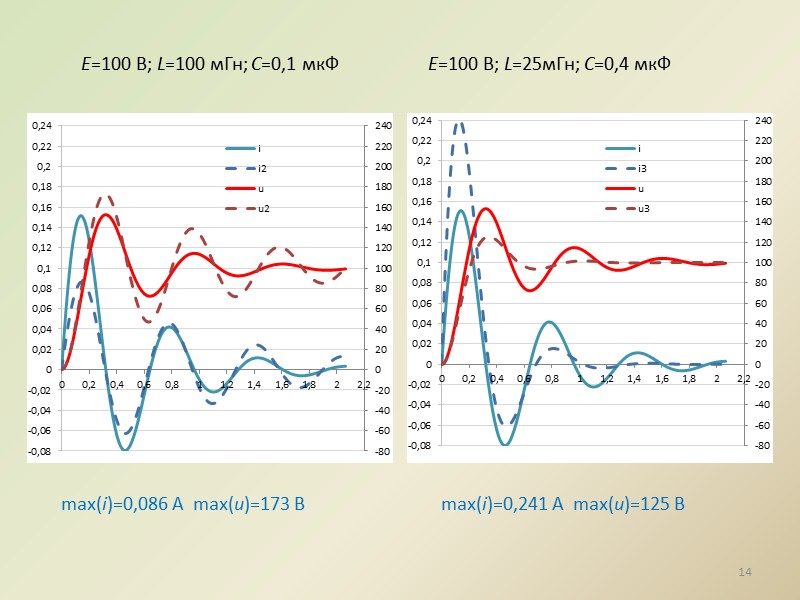
14 E=100 В; L=100 мГн; С=0,1 мкФ E=100 В; L=25мГн; С=0,4 мкФ max(i)=0,086 А max(u)=173 В max(i)=0,241 А max(u)=125 В

Контур 2 порядка при периодическом синусоидальном воздействии л3 15

; - фаза вынужденной составляющей - угол потерь контура , т.е. угол фазового сдвига между Uc и e(t) в установившемся режиме; - амплитуды вынужденных составляющих напряжения на емкости и тока - модуль входного сопротивления контура на частоте  - фаза переходной составляющей -начальная амплитуда переходной составляющей по отношению к 16 Условие резонанса

Собственные значения и собственные векторы. Роль в решении СДУ Собственным вектором квадратной матрицы A называют ненулевой столбец wk , для которого где k  некоторое число, являющееся соответствующим собственным числом матрицы A. 17

Решение однородной системы линейных дифференциальных уравнений различными способами Схема с Классический способ решения. Система ДУ 1 ДУ высокого порядка Нач. усл. для производной Частн. реш-е общее решение Матричная запись решения 18

Решение в матричном виде ; - вектор - вектор и - числа ; - частное решение собственные значения – корни характеристического уравнения, или нули определителя ; собственные векторы – решения системы для найденных , причем решение этой задачи возможно только с точностью до произвольного постоянного. Составим общее решение: Определение - критическое место решения! 19

Решение в виде матричного ряда - матричный ряд Тейлора Производная от этого решения приводит к исходному уравнению Ряд в - экспоненциальная функция от матрицы А, называется матричной экспонентой: Окончательный вид решения: 20

Анализ различных способов решения систем дифференциальных уравнений л.4 Из единственности решения следует, что решения и эквивалентны , тогда: Отсюда следует равенство: - диагональная матрица (ДМ) Доказательство: , тогда ряд Тейлора примет вид: Следствия. 1. Любая функция от ДМ, если только она представима рядом Тейлора, есть функция от ее диагональных элементов. 2. Нахождение решения системы дифференциальных уравнений полностью определяется нахождением таких матриц  и W , которые удовлетворяют соотношению или (*) Если найдено разложение (*), тогда: Отсюда получаем n независимых уравнений 21

Физический смысл собственных значений в задачах электроэнергетики 22 собственные значения комплексные и попарно сопряженные, переходный процесс затухающий колебательный собственные значения вещественные и равные (кратные), переходный процесс апериодический собственные значения чисто вещественные и различные, переходный процесс апериодический собственные значения чисто мнимые и сопряженные, переходный процесс колебательный незатухающий Физический смысл собственных значений. Собственные значения матрицы коэффициентов систем дифференциальных уравнений, разрешенных относительно производных и описывающих переходные процессы в схемах с сосредоточенными параметрами, определяют: мнимые части – частоты собственных колебаний схем, вещественные части – затухания на этих частотах. Собственные векторы дают соотношения амплитуд колебаний на различных частотах.

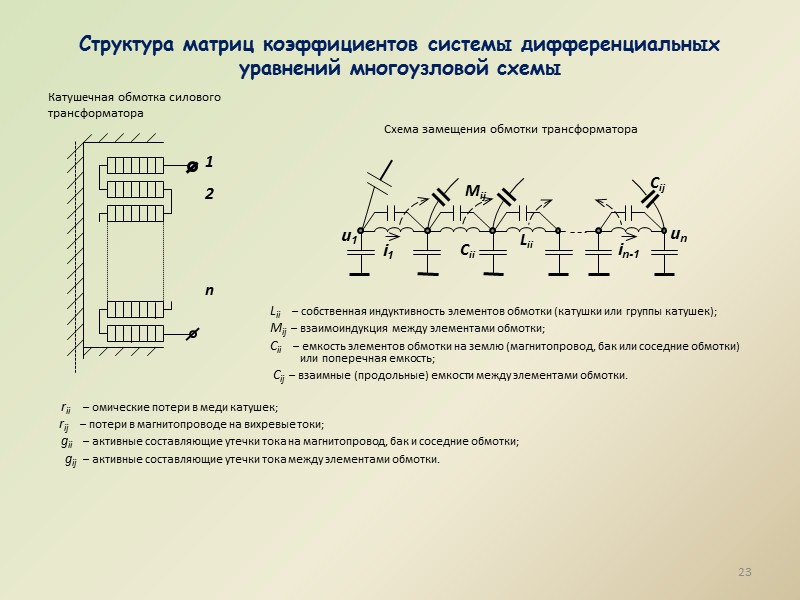
Структура матриц коэффициентов системы дифференциальных уравнений многоузловой схемы Катушечная обмотка силового трансформатора Схема замещения обмотки трансформатора Lii – собственная индуктивность элементов обмотки (катушки или группы катушек); Mij – взаимоиндукция между элементами обмотки; Cii – емкость элементов обмотки на землю (магнитопровод, бак или соседние обмотки) или поперечная емкость; Cij – взаимные (продольные) емкости между элементами обмотки. rii – омические потери в меди катушек; rij – потери в магнитопроводе на вихревые токи; gii – активные составляющие утечки тока на магнитопровод, бак и соседние обмотки; gij – активные составляющие утечки тока между элементами обмотки. 23

Первая система дифференциальных уравнений : разности напряжений в соседних узлах, которые определяются токами во всех ветвях схемы 24

Вторая система дифференциальных уравнений : суммы токов в узлах (положительное направление - к узлам) 25

Системы дифференциальных уравнений многоузловой схемы без потерь R = 0 и G = 0 : - обобщенная алгебраическая проблема с.зн. B и L – симметричные матрицы - с.м. А – несимметричная матрица !!! с.м. с.м. Разложение Холецкого: ( - верхняя треугольная матрица) с.м. У любой симметричной и эрмитовой матрицы собственные значения – вещественные числа. Матрица M – положительно определенная (матрица, у которой диагональные элементы значительно больше внедиагональных), следовательно, все собственные значения будут больше нуля, а 26

Алгебраическая проблема собственных значений. Преобразование подобия Основное свойство преобразования подобия (и только его) : сохранение собственных значений матрицы A. Матрица C, вне зависимости от вида матрицы B, имеет те же собственные значения, что и матрица A. Доказательство. Характеристический многочлен А: Характеристический многочлен С: , где М1 и М2 – вещественные симметричные матрицы; VT и V – ортогональные матрицы. , где М1 и М2 – эрмитовы матрицы; RH и R – унитарные матрицы. - ортогональная матрица является матрица простых вращений (поворот вектора в плоскости на угол ) 27

Метод Якоби (1846 г.) л.5 Метод Якоби – первый из группы методов вращения. (Классический М.Я., М.Я. с преградами, м. Гивенса, м. Стрелкова) Матрицы – вещественные симметричные, метод итерационный, сходимость высокая. Теоретическая основа метода : исходная м-ца преобразуется в диагональную с помощью последовательных плоских вращений. На каждой итерации исключается максимальный по модулю внедиагональный элемент исходной матрицы , коэффициентов СДУ. - исходная м-ца, - макс. внедиагональный элемент. Шаг 1. Умножаем последовательно: А) все строки матрицы на все столбцы , кроме -го и -го: получаем столбцы Б) i0 –й столбец В: В) j0 –й столбец В: 2 столбца матрицы В отличаются от матрицы . 28

Шаг 2. Умножаем последовательно А) все строки матрицы , кроме i0 -й и j0 –й , на столбцы В: Б) i0-я строка М1 В) j0-я строка М1 2 строки и 2 столбца М1 отличаются от М0. Цель: Однако! Нули «портятся» , поэтому метод итерационный. Число итераций: Метод Якоби с преградами 29

QR – алгоритм (1961 г.) 1 этап. Приведение А к форме Хессенберга. Используем метод Гивенса (неитерационный, вращения в плоскости , не портятся нули, но для симметричной матрицы получим трехдиагональную, для несимметричной – Форму Хессенберга) . 2 этап. Разложение А0 по методу Грамма-Шмидта : R0 - верхняя треугольная матрица, диагональные элементы которой вещественны и положительны Q0 - унитарная матрица - верхняя треугольная с с.зн. на диагонали Разложение Грамма-Шмидта : 30

Связь векторов нулевого приближения матрицы А с элементами матриц R и Q : и - векторы, r11 – скаляр. Эвклидова норма: (т.к. Q – унитарная) Умножим 2-е уравнение на слева На каждом j-м шаге 31

Применимость методов определения с.зн. и с.в. метод Якоби классический – для вещественных симметричных матриц, итерационный метод Якоби с преградами – для вещественных симметричных матриц, итерационный метод Якоби для Эрмитовых матриц (комплексных, симметричных), итерационный метод Гивенса – для вещественных симметричных матриц, неитерационный, приводит к трехдиагональной симметричной матрице метод деления пополам – для трехдиагональных симметричных матриц, итерационный метод Стрелкова – для комплексных несимметричных матриц  до 35 порядка, итерационный QR-алгоритм – для комплексных несимметричных матриц большого порядка, итерационный 32

Решение неоднородных систем линейных дифференциальных уравнений с помощью интегральных преобразований. Особенности применения интегрального преобразования Фурье в электротехнике Ряд Фурье в тригонометрической и комплексной форме - основная круговая частота функции - линейчатый спектр гармоник Интегральное преобразование Фурье. Для апериодических функций Т , 33