Пусть заданы две прямые 11 bxky 22 bxky

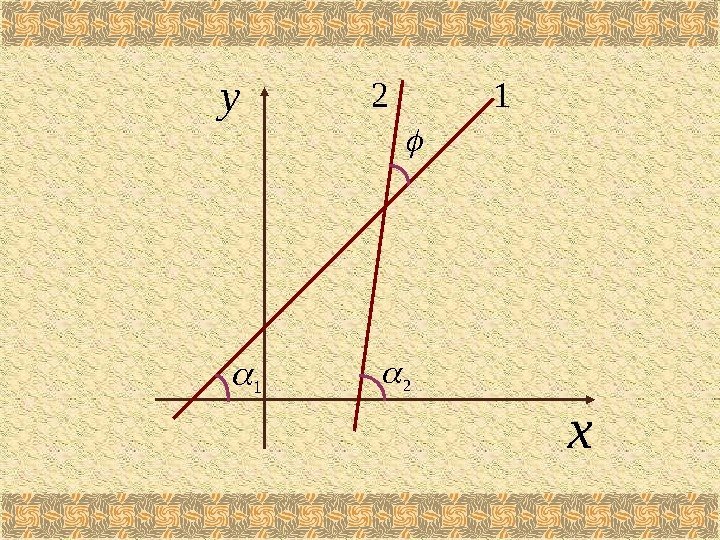
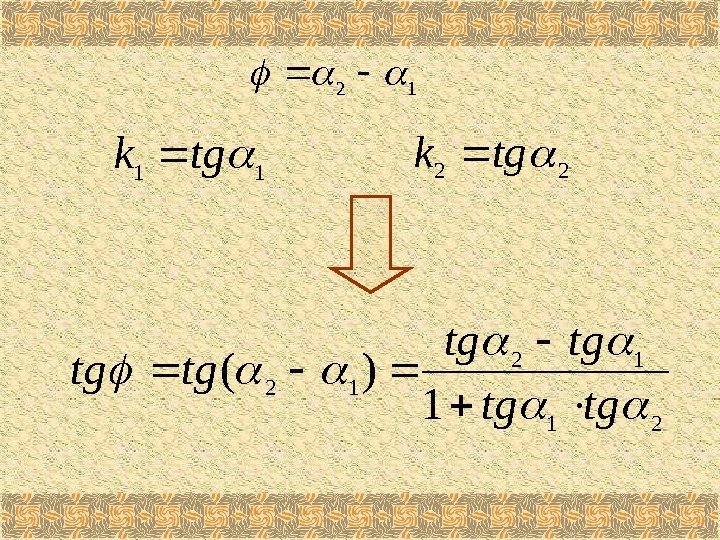













4.2..ppt
- Размер: 377.5 Кб
- Автор:
- Количество слайдов: 18
Описание презентации Пусть заданы две прямые 11 bxky 22 bxky по слайдам
 Пусть заданы две прямые 11 bxky 22 bxky Выразим угол между этими прямыми через их угловые коэффициенты.
Пусть заданы две прямые 11 bxky 22 bxky Выразим угол между этими прямыми через их угловые коэффициенты.
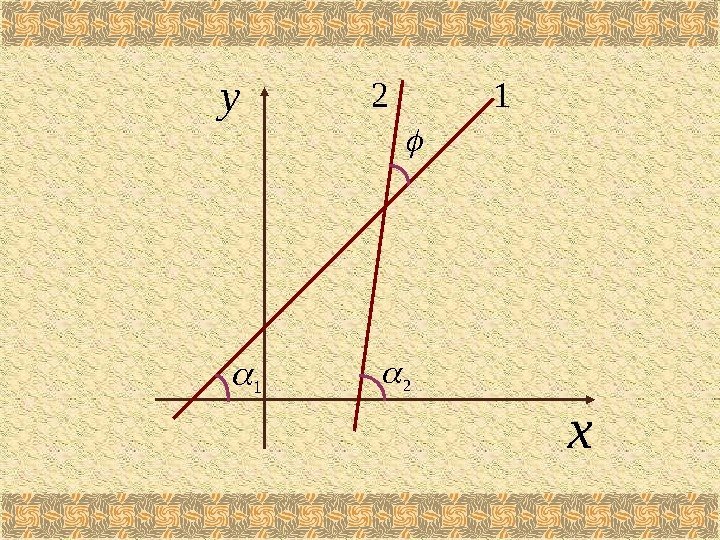 xy
xy
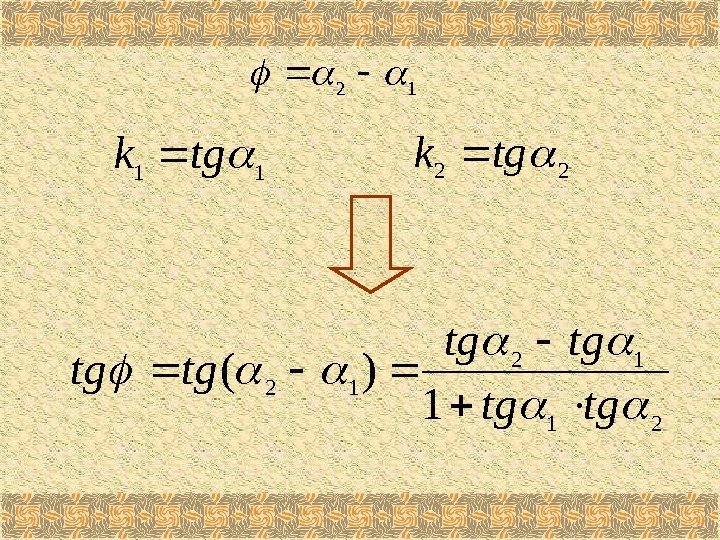 12 11 tgk 22 tgk 21 12 12 1 )( tgtg
12 11 tgk 22 tgk 21 12 12 1 )( tgtg
 21 12 1 kk kk tg Стрелка указывает, что угол отсчитывается против часовой стрелки от прямой 1 к прямой 2.
21 12 1 kk kk tg Стрелка указывает, что угол отсчитывается против часовой стрелки от прямой 1 к прямой 2.
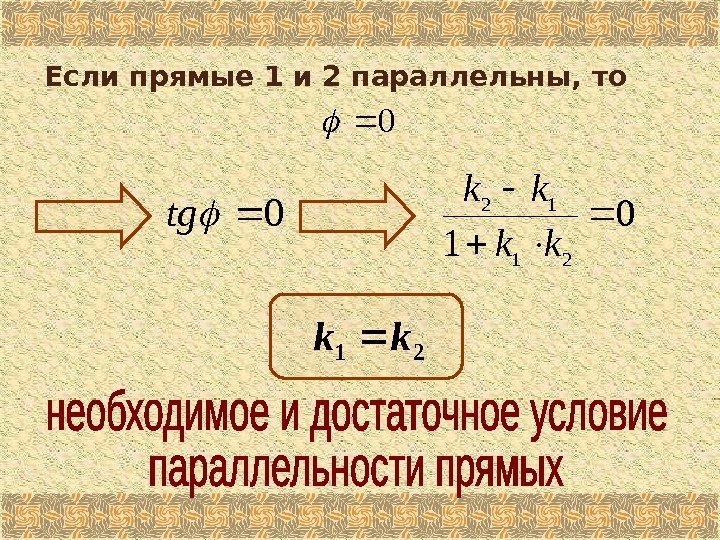
 Если прямые 1 и 2 параллельны, то 0 0 tg 0 1 21 12 kk kk 21 kk
Если прямые 1 и 2 параллельны, то 0 0 tg 0 1 21 12 kk kk 21 kk
 Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны.
Две прямые параллельны тогда и только тогда, когда их угловые коэффициенты равны.
 Если прямые 1 и 2 перпендикулярны, то 2 0 2 ctgctg 0 11 12 21 kk kk tg ctg 2 1 1 k k
Если прямые 1 и 2 перпендикулярны, то 2 0 2 ctgctg 0 11 12 21 kk kk tg ctg 2 1 1 k k
 Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Две прямые перпендикулярны тогда и только тогда, когда их угловые коэффициенты обратны по величине и противоположны по знаку.
 Если прямые заданы общими уравнениями 2 1 B B A A 0111 Cy. Bx. A 0 222 Cy. Bx.
Если прямые заданы общими уравнениями 2 1 B B A A 0111 Cy. Bx. A 0 222 Cy. Bx.
 Пусть даны две прямые 0111 Cy. Bx. A 0 222 Cy. Bx. A Если они не параллельны, то можно найти точку их пересечения. Т. к. эта точка принадлежит обеим прямым, то ее координаты должны удовлетворять системе уравнений: 0 0 222 111 Cy. Bx. A Решение этой системы дает единственную точку пересечения.
Пусть даны две прямые 0111 Cy. Bx. A 0 222 Cy. Bx. A Если они не параллельны, то можно найти точку их пересечения. Т. к. эта точка принадлежит обеим прямым, то ее координаты должны удовлетворять системе уравнений: 0 0 222 111 Cy. Bx. A Решение этой системы дает единственную точку пересечения.
 ПРИМЕР. Составить уравнения прямых, проходящих через точку А(2, 1), одна из которых параллельна, а другая перпендикулярна прямой 0223 yx
ПРИМЕР. Составить уравнения прямых, проходящих через точку А(2, 1), одна из которых параллельна, а другая перпендикулярна прямой 0223 yx
 РЕШЕНИЕ: 1. По условию параллельности прямых Найдем угловой коэффициент заданной прямой: Тогд а 21 kk 0223 yx 23 1 231 kxy 23 2 k bxy 23 Т. к. точка А лежит на искомой прямой, то ее координаты удовлетворяют этому уравнению:
РЕШЕНИЕ: 1. По условию параллельности прямых Найдем угловой коэффициент заданной прямой: Тогд а 21 kk 0223 yx 23 1 231 kxy 23 2 k bxy 23 Т. к. точка А лежит на искомой прямой, то ее координаты удовлетворяют этому уравнению:
 И уравнение искомой прямой будет: 04322 23 xyxy 2. По условию перпендикулярности прямых b 2 23 12 b 21 1 kk Найдем угловой коэффициент искомой прямой:
И уравнение искомой прямой будет: 04322 23 xyxy 2. По условию перпендикулярности прямых b 2 23 12 b 21 1 kk Найдем угловой коэффициент искомой прямой:
 32 3 k bxy 32 Снова координаты точки А удовлетворяют этому уравнению: 37 b b 2 32 1 И уравнение искомой прямой будет: 0723 3 7 3 2 xyxy
32 3 k bxy 32 Снова координаты точки А удовлетворяют этому уравнению: 37 b b 2 32 1 И уравнение искомой прямой будет: 0723 3 7 3 2 xyxy
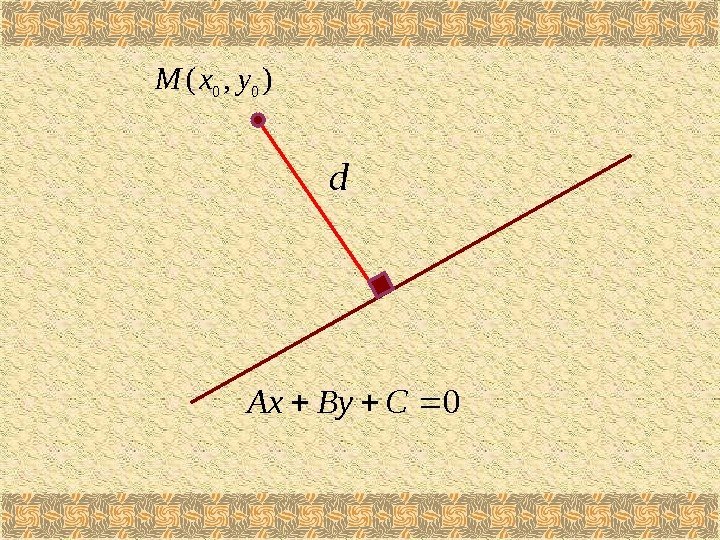
 Пусть дана точка М(х 0 , у 0 ) и прямая Под расстоянием от точки М до прямой понимается длина перпендикуляра d , опущенного из точки М на данную прямую. 0 CBy. Ax 22 00 BA CBy. Ax d
Пусть дана точка М(х 0 , у 0 ) и прямая Под расстоянием от точки М до прямой понимается длина перпендикуляра d , опущенного из точки М на данную прямую. 0 CBy. Ax 22 00 BA CBy. Ax d
 ), (00 yx. M 0 CBy. Ax d
), (00 yx. M 0 CBy. Ax d
 ПРИМЕР. Найти расстояние между параллельными прямыми 064302443 yxyx
ПРИМЕР. Найти расстояние между параллельными прямыми 064302443 yxyx
 РЕШЕНИЕ: Возьмем на одной из прямых, например, на первой, произвольную точку А(0, 6). Тогда искомое расстояние это перпендикуляр от точки А до второй прямой : 643 CBA 6 43 66403 22 d
РЕШЕНИЕ: Возьмем на одной из прямых, например, на первой, произвольную точку А(0, 6). Тогда искомое расстояние это перпендикуляр от точки А до второй прямой : 643 CBA 6 43 66403 22 d
