Описание презентации Пусть прямая задана уравнением: И пусть задана плоскость по слайдам
 Пусть прямая задана уравнением: И пусть задана плоскость p zz n yy m xx 111 0 DCz. By. Ax Рассмотрим возможные случаи ориентации прямой и плоскости:
Пусть прямая задана уравнением: И пусть задана плоскость p zz n yy m xx 111 0 DCz. By. Ax Рассмотрим возможные случаи ориентации прямой и плоскости:
 1 Прямая принадлежит плоскости. ортогонален нормальному вектору плоскости), , (pnms ), , (CBAn И пусть точка. Тогда направляющий вектор прямой ), , ( 0000 zyx. M принадлежит прямой.
1 Прямая принадлежит плоскости. ортогонален нормальному вектору плоскости), , (pnms ), , (CBAn И пусть точка. Тогда направляющий вектор прямой ), , ( 0000 zyx. M принадлежит прямой.
 Тогда выполняются следующие условия: иs n в этом случае перпендикулярны, и их скалярное произведение этих векторов равно нулю: Поскольку вектора 0), (Cp. Bn. Amsn Поскольку точка М 0 будет принадлежать плоскости, то ее координаты удовлетворяют уравнению плоскости: 0 000 DCz. By. Ax
Тогда выполняются следующие условия: иs n в этом случае перпендикулярны, и их скалярное произведение этих векторов равно нулю: Поскольку вектора 0), (Cp. Bn. Amsn Поскольку точка М 0 будет принадлежать плоскости, то ее координаты удовлетворяют уравнению плоскости: 0 000 DCz. By. Ax
 2 Прямая параллельна плоскости. Прямая пересекает плоскость в одной точке. Тогда выполняется условие. Тогда выполняется только условие (1). 30), (Cp. Bn. Amsn
2 Прямая параллельна плоскости. Прямая пересекает плоскость в одной точке. Тогда выполняется условие. Тогда выполняется только условие (1). 30), (Cp. Bn. Amsn
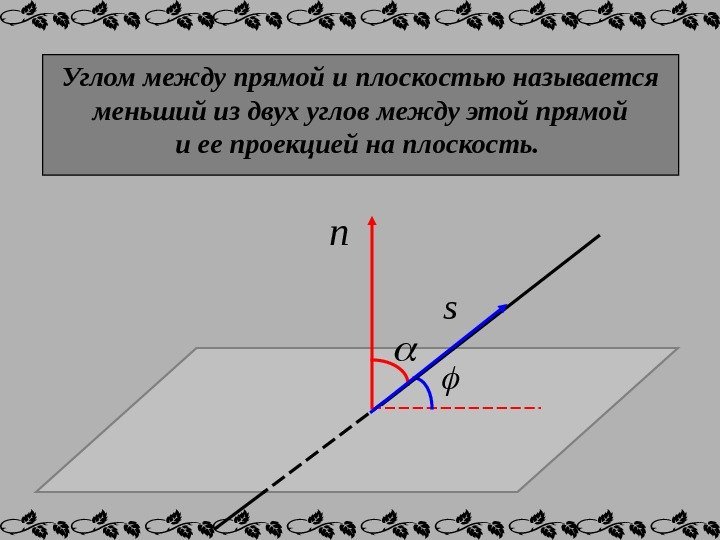 Углом между прямой и плоскостью называется меньший из двух углов между этой прямой и ее проекцией на плоскость. n s
Углом между прямой и плоскостью называется меньший из двух углов между этой прямой и ее проекцией на плоскость. n s
 Синус угла φ между прямой и плоскостью равен косинусу угла α между нормальным вектором плоскости и направляющим вектором прямой: Найдем угол α , как угол между двумя векторами: cossin 222222 cos pnm. CBA Cp. Bn. Am
Синус угла φ между прямой и плоскостью равен косинусу угла α между нормальным вектором плоскости и направляющим вектором прямой: Найдем угол α , как угол между двумя векторами: cossin 222222 cos pnm. CBA Cp. Bn. Am
 222222 sin pnm. CBA Cp. Bn. Am
222222 sin pnm. CBA Cp. Bn. Am
 p C n B m A Если прямая перпендикулярна плоскости, то направляющий вектор прямой параллелен нормальному вектору плоскости: ns ||
p C n B m A Если прямая перпендикулярна плоскости, то направляющий вектор прямой параллелен нормальному вектору плоскости: ns ||
 0 Cp. Bn. Am. Если прямая параллельна плоскости, то ns
0 Cp. Bn. Am. Если прямая параллельна плоскости, то ns

















