Описание презентации Пусть плоскость Р , проходит через по слайдам
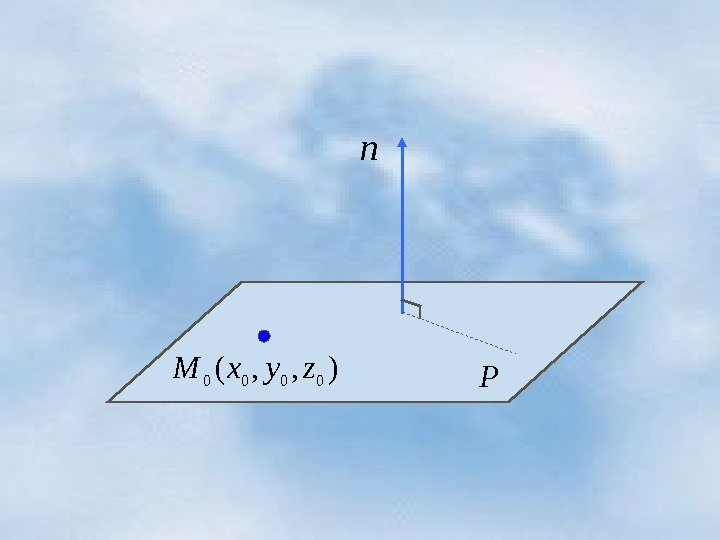
 Пусть плоскость Р , проходит через заданную точку), , (CBAn и перпендикулярна вектору ), , ( 0000 zyx. M Этот вектор называется нормальным вектором плоскости Р.
Пусть плоскость Р , проходит через заданную точку), , (CBAn и перпендикулярна вектору ), , ( 0000 zyx. M Этот вектор называется нормальным вектором плоскости Р.
 P n ), , ( 0000 zyx. M
P n ), , ( 0000 zyx. M
 Выберем на плоскости произвольную точку ), , (0000 zzyyxx. MM Тогда ), , (zyx. M и n. MM 0 Распишем его в координатах: 0)()()(), (0000 zz. Cyy. Bxx. An. MM Тогда скалярное произведение этих векторов должно быть равно нулю: 0), ( 0 n. MM
Выберем на плоскости произвольную точку ), , (0000 zzyyxx. MM Тогда ), , (zyx. M и n. MM 0 Распишем его в координатах: 0)()()(), (0000 zz. Cyy. Bxx. An. MM Тогда скалярное произведение этих векторов должно быть равно нулю: 0), ( 0 n. MM
 10)()()(000 zz. Cyy. Bxx.
10)()()(000 zz. Cyy. Bxx.
 Раскроем скобки в уравнении (1): 0000 Cz. By. Ax. Ax Обозначим: DCz. By. Ax
Раскроем скобки в уравнении (1): 0000 Cz. By. Ax. Ax Обозначим: DCz. By. Ax
 20 DCz. By. Ax
20 DCz. By. Ax
 Пусть плоскость Р отсекает на осях координат отрезки, равные соответственно a, b, c. xy z a bc
Пусть плоскость Р отсекает на осях координат отрезки, равные соответственно a, b, c. xy z a bc
 31 c z b y a x
31 c z b y a x
 Пусть задана плоскость, проходящая через три точки: ), , ( 1111 zyx. M), , (2222 zyx. M), , (3333 zyx. M Тогда уравнение этой плоскости можно записать в виде равенства нулю определителя:
Пусть задана плоскость, проходящая через три точки: ), , ( 1111 zyx. M), , (2222 zyx. M), , (3333 zyx. M Тогда уравнение этой плоскости можно записать в виде равенства нулю определителя:
 40 131313 121212 111 zzyyxx
40 131313 121212 111 zzyyxx
 Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности их нормальных векторов: Пусть даны две плоскости с нормальными векторами), , (1111 CBAn ), , (2222 CBAn 21 ||nn
Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности их нормальных векторов: Пусть даны две плоскости с нормальными векторами), , (1111 CBAn ), , (2222 CBAn 21 ||nn
 И плоскость. Пусть дана точка ), , ( 0000 zyx. M 0 DCz. By. Ax Тогда расстояние от точки до плоскости определяется по формуле:
И плоскость. Пусть дана точка ), , ( 0000 zyx. M 0 DCz. By. Ax Тогда расстояние от точки до плоскости определяется по формуле:
 222 000 CBA DCz. By. Ax d
222 000 CBA DCz. By. Ax d















