Производная по направлению и градиент функции Часть 1

Производная по направлению и градиент функции Часть 1 Производная по направлению

Для характеристики скорости изменения поля в заданном направлении введём понятие «производной по направлению» . Возьмём в пространстве, где задано поле , некоторую точку M и найдём скорость изменения функций U при движении точки М в произвольном направлении . Пусть вектор имеет начало в точке M и направляющие косинусы Приращение функций U, возникающее при переходе от точки к некоторой точке в направлении вектора определяется как или )( MUU ), , ( zyx. UU . cos, cos M 1 ), ()(1 MUMUU ); ; (zyx. Uzzyyxx. UU

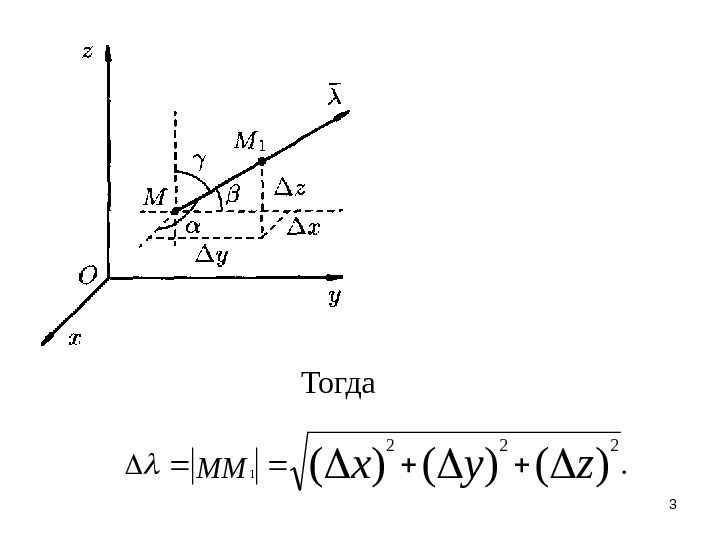
Тогда . )()()(222 1 zyx. MM

Производной от функции в точке М по направлению называется предел )( MUU MM MUMUUU MM 1 1 0 )()( limlim

Производная по направлению и характеризует скорость изменения функции (поля) в точке М по этому направлению. Если , то функция U возрастает в направлении , если , то функция U в направлении убывает. Кроме того, величина представляет собой мгновенную скорость изменения функции U в направлении в точке М : чем больше , тем быстрее изменяется функция U. В этом состоит физический смысл производной по направлению. 0 U U U

Переходя к пределу при , получим формулу для вычисления производной по направлению : 0 coscoscos z U y U x UU 6)1(

Пример Найти производную функции в точке в направлении от этой точки к точке Решение : Находим вектор и его направляющие косинусы : yzyx. U 42 2)2; 1; 0(M ). 3; 3; 2( 1 M MM 1 ), 1; 2; 2(1 MM. 3 1 cos, 3 2 144 2 cos

Находим частные производные функции и вычисляем их значения в точке M : , 2 x x U , 42 zy y U , 4 y z. U , 002 x U M , 6242 y. U M. 4 z. U M

Следовательно, по формуле (1) имеем : Поскольку то заданная функция в данном направлении убывает. . 3 16 3 1 4 3 2 6 3 2 0 U M , 0 U