Производная и дифференциал Непрерывность функции Если функция непрерывна

























11-4-proizvodnaya_i_differencial.ppt
- Количество слайдов: 39
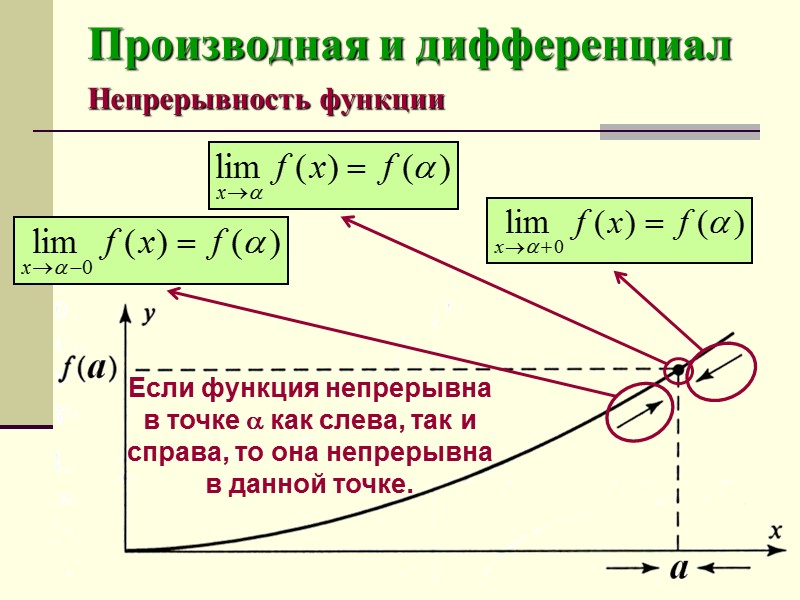
 Производная и дифференциал Непрерывность функции Если функция непрерывна в точке как слева, так и справа, то она непрерывна в данной точке.
Производная и дифференциал Непрерывность функции Если функция непрерывна в точке как слева, так и справа, то она непрерывна в данной точке.
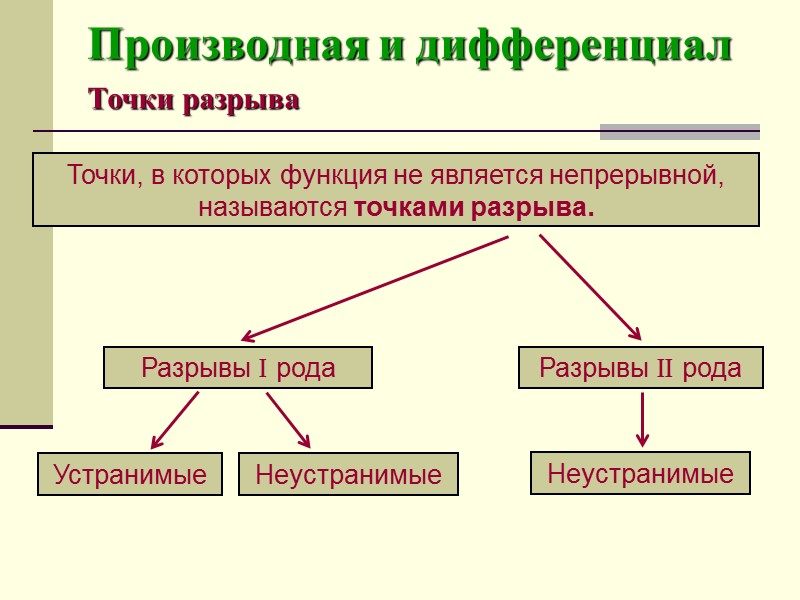
 Производная и дифференциал Точки разрыва Точки, в которых функция не является непрерывной, называются точками разрыва. Разрывы I рода Разрывы II рода Устранимые Неустранимые Неустранимые
Производная и дифференциал Точки разрыва Точки, в которых функция не является непрерывной, называются точками разрыва. Разрывы I рода Разрывы II рода Устранимые Неустранимые Неустранимые
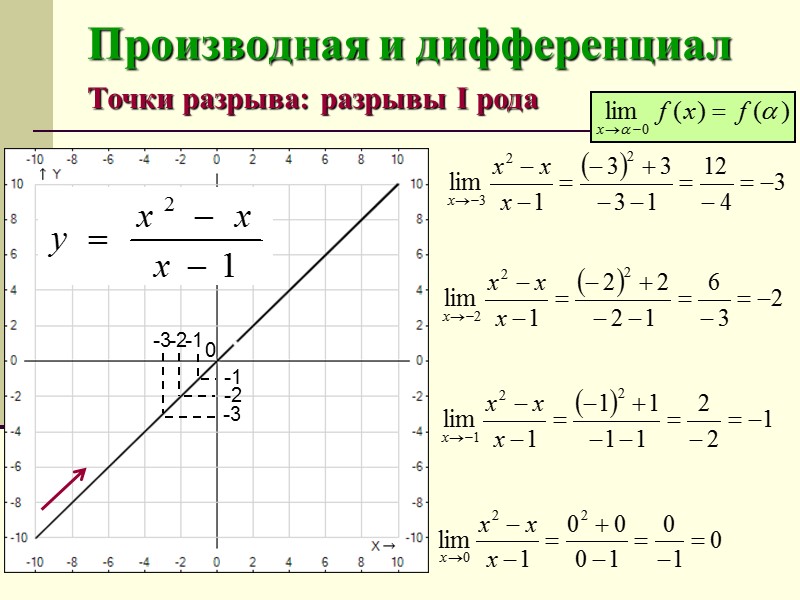
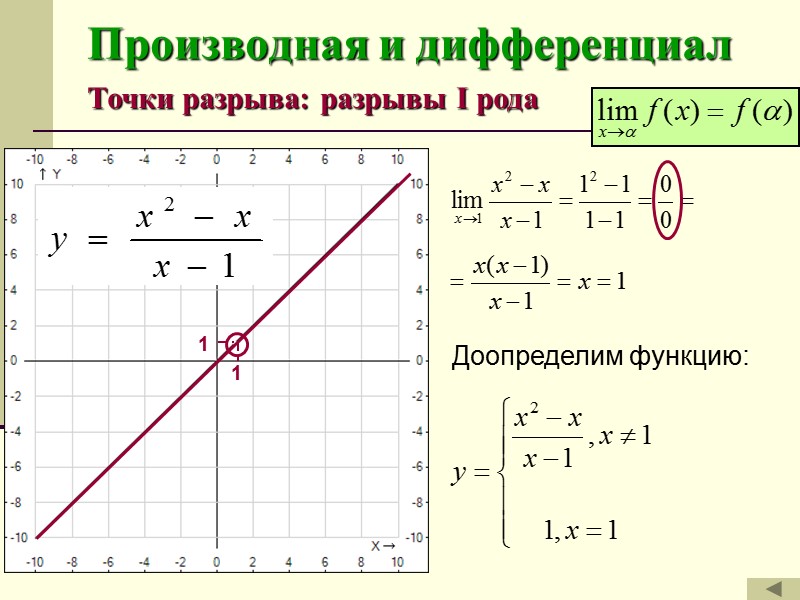
 Производная и дифференциал Точки разрыва: разрывы I рода Если функция в точке имеет конечный двусторонний предел, но этот предел отличен от значения функции в этой точке (или точка не входит в область определения функции), то точка называется устранимой точкой разрыва.
Производная и дифференциал Точки разрыва: разрывы I рода Если функция в точке имеет конечный двусторонний предел, но этот предел отличен от значения функции в этой точке (или точка не входит в область определения функции), то точка называется устранимой точкой разрыва.
 Производная и дифференциал Точки разрыва: разрывы I рода -3 -3 -2 -2 -1 -1 0
Производная и дифференциал Точки разрыва: разрывы I рода -3 -3 -2 -2 -1 -1 0
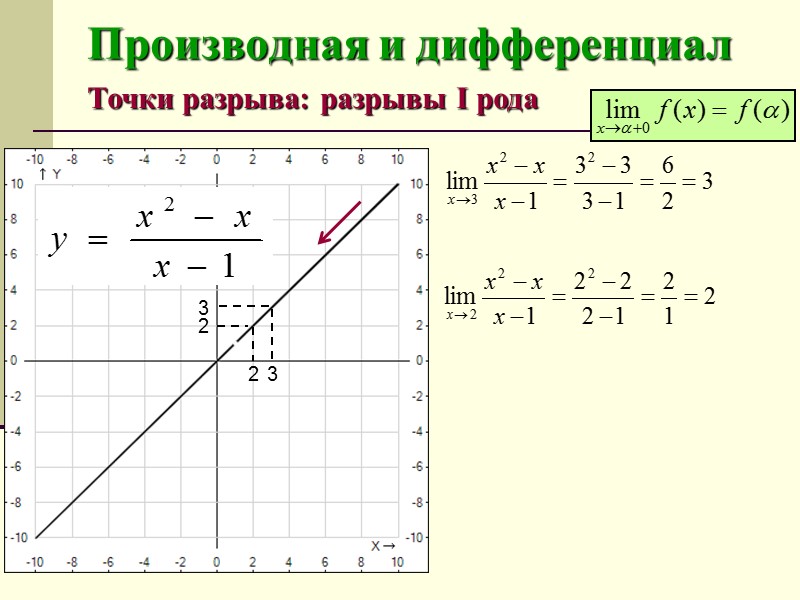
 Производная и дифференциал Точки разрыва: разрывы I рода 3 3 2 2
Производная и дифференциал Точки разрыва: разрывы I рода 3 3 2 2
 Производная и дифференциал Точки разрыва: разрывы I рода 1 1 Доопределим функцию:
Производная и дифференциал Точки разрыва: разрывы I рода 1 1 Доопределим функцию:
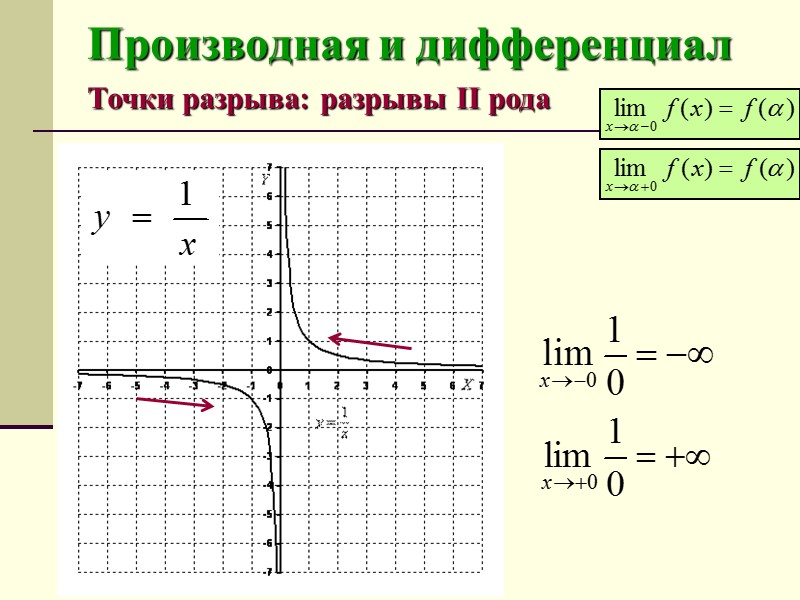
 Производная и дифференциал Точки разрыва: разрывы II рода Если функция в точке не имеет конечного левого, правого или обоих пределов, то функция не является неразрывной в точке , и эта точка называется неустранимой точкой разрыва.
Производная и дифференциал Точки разрыва: разрывы II рода Если функция в точке не имеет конечного левого, правого или обоих пределов, то функция не является неразрывной в точке , и эта точка называется неустранимой точкой разрыва.
 Производная и дифференциал Точки разрыва: разрывы II рода
Производная и дифференциал Точки разрыва: разрывы II рода
 Производная и дифференциал Свойства непрерывности функции Если функции f(x) и g(x) непрерывны в точке , то функция f(x) g(x), f(x)* g(x) и f(x) / g(x) (при условии, что g() ≠ 0) непрерывны в этой точке. Если функция u=g(x) непрерывна в точке и функция y=f(u) непрерывна в точке g(), то сложная функция y=f(g(x)) также непрерывна в точке . Элементарные функции непрерывны в области их определения.
Производная и дифференциал Свойства непрерывности функции Если функции f(x) и g(x) непрерывны в точке , то функция f(x) g(x), f(x)* g(x) и f(x) / g(x) (при условии, что g() ≠ 0) непрерывны в этой точке. Если функция u=g(x) непрерывна в точке и функция y=f(u) непрерывна в точке g(), то сложная функция y=f(g(x)) также непрерывна в точке . Элементарные функции непрерывны в области их определения.
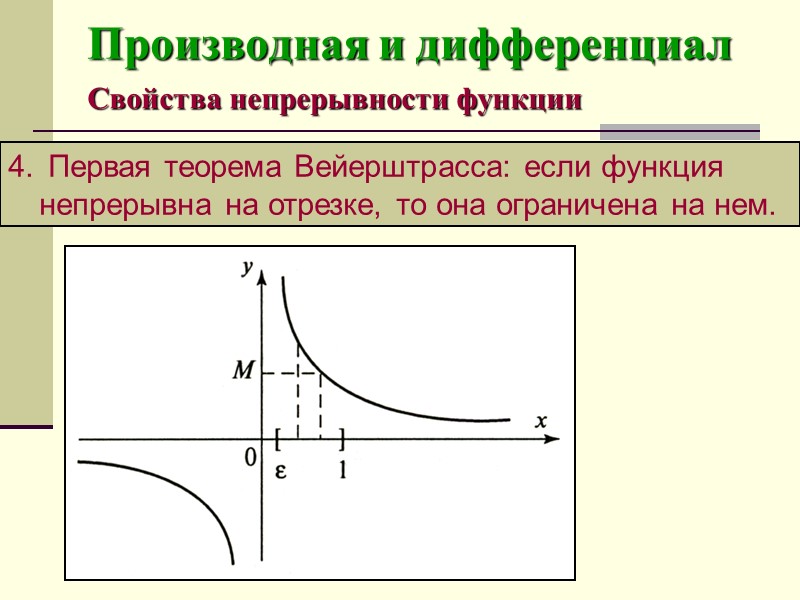
 Производная и дифференциал Свойства непрерывности функции Первая теорема Вейерштрасса: если функция непрерывна на отрезке, то она ограничена на нем.
Производная и дифференциал Свойства непрерывности функции Первая теорема Вейерштрасса: если функция непрерывна на отрезке, то она ограничена на нем.
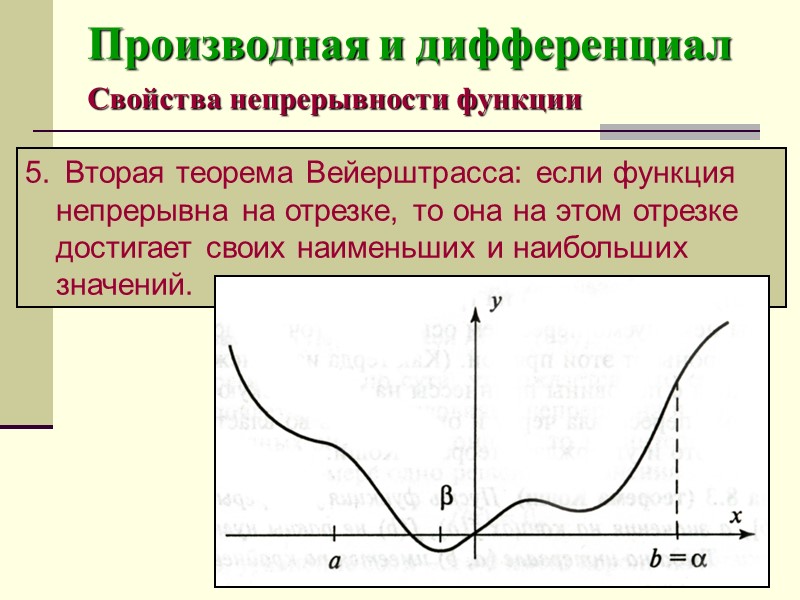
 Производная и дифференциал Свойства непрерывности функции Вторая теорема Вейерштрасса: если функция непрерывна на отрезке, то она на этом отрезке достигает своих наименьших и наибольших значений.
Производная и дифференциал Свойства непрерывности функции Вторая теорема Вейерштрасса: если функция непрерывна на отрезке, то она на этом отрезке достигает своих наименьших и наибольших значений.
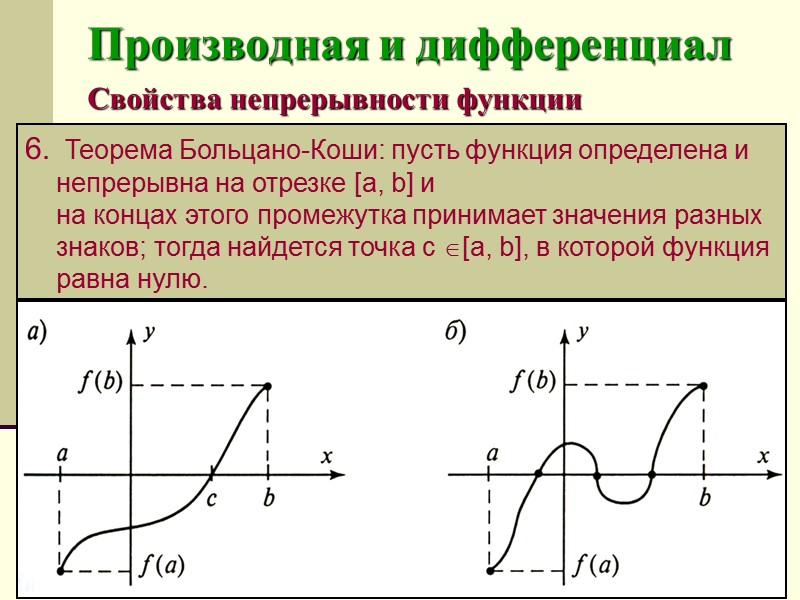
 Производная и дифференциал Свойства непрерывности функции Теорема Больцано-Коши: пусть функция определена и непрерывна на отрезке [а, b] и на концах этого промежутка принимает значения разных знаков; тогда найдется точка с [а, b], в которой функция равна нулю.
Производная и дифференциал Свойства непрерывности функции Теорема Больцано-Коши: пусть функция определена и непрерывна на отрезке [а, b] и на концах этого промежутка принимает значения разных знаков; тогда найдется точка с [а, b], в которой функция равна нулю.
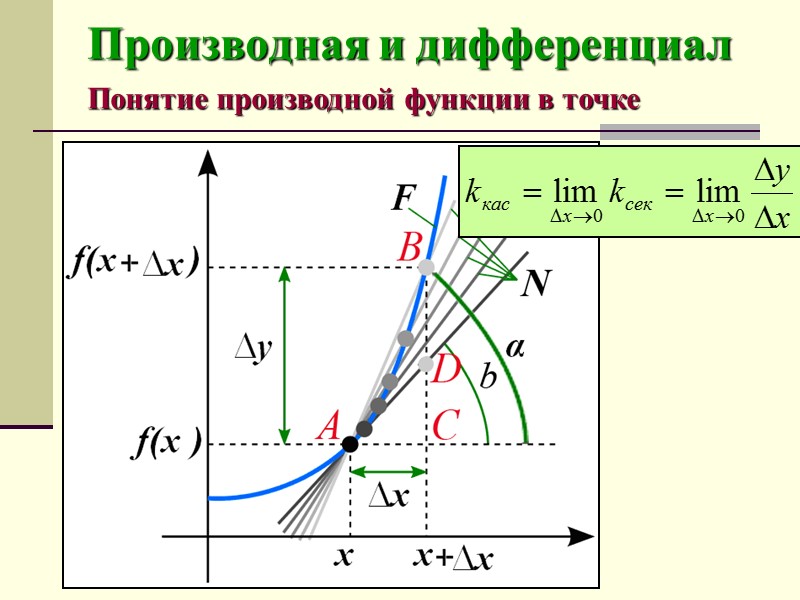
 Производная и дифференциал Понятие производной функции в точке Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).
Производная и дифференциал Понятие производной функции в точке Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).
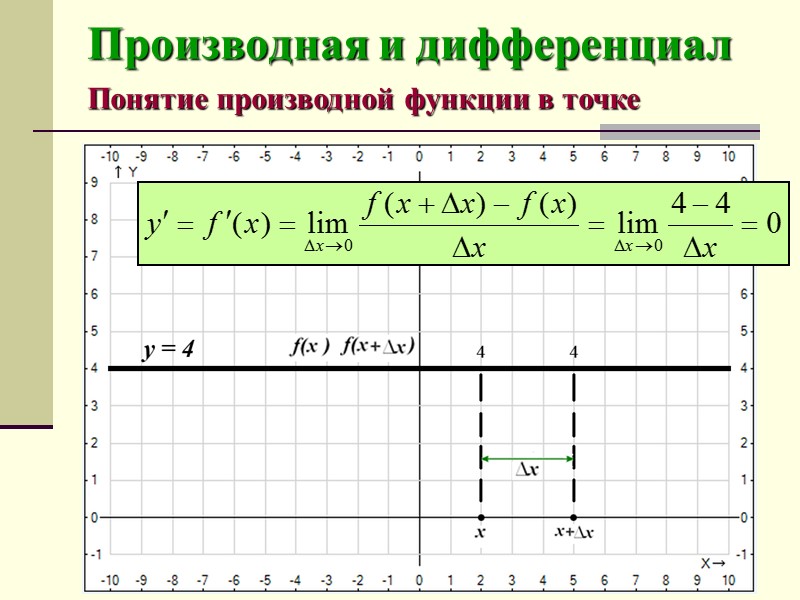
 Производная и дифференциал Понятие производной функции в точке
Производная и дифференциал Понятие производной функции в точке
 Производная и дифференциал Понятие производной функции в точке Чтобы найти производную f(x) в точке х, необходимо: определить значения этой функции в точке х и в точке x+Δx, где Δx – приращение аргумента х; найти приращение функции Δy = f(x+Δx) – f(x); найти предел (если он существует) отношения приращение функции к приращению аргумента.
Производная и дифференциал Понятие производной функции в точке Чтобы найти производную f(x) в точке х, необходимо: определить значения этой функции в точке х и в точке x+Δx, где Δx – приращение аргумента х; найти приращение функции Δy = f(x+Δx) – f(x); найти предел (если он существует) отношения приращение функции к приращению аргумента.
 Производная и дифференциал Понятие производной функции в точке Предел отношения Δу/Δх=tgВАС(b) tgDАС(а) при Δх 0 (если таковой существует), называется производной функции у = f(x) в точке х.
Производная и дифференциал Понятие производной функции в точке Предел отношения Δу/Δх=tgВАС(b) tgDАС(а) при Δх 0 (если таковой существует), называется производной функции у = f(x) в точке х.
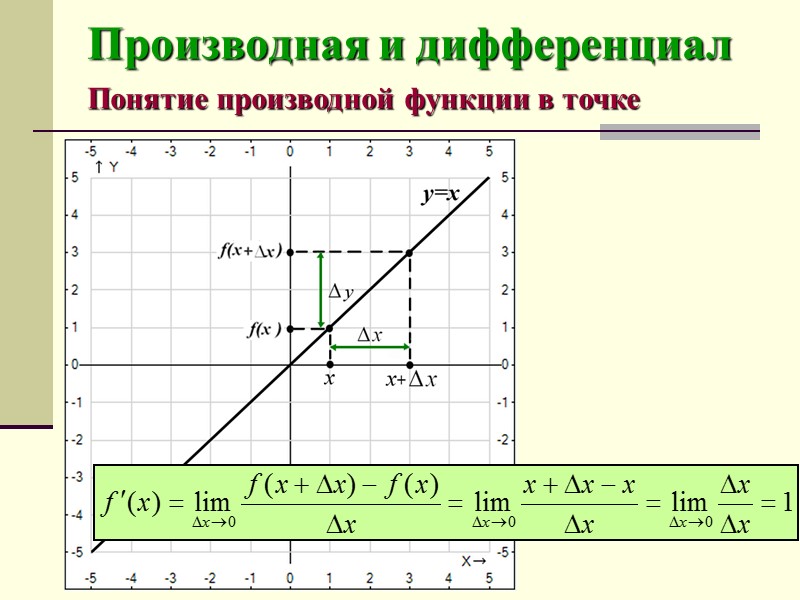
 Производная и дифференциал Понятие производной функции в точке
Производная и дифференциал Понятие производной функции в точке
 Производная и дифференциал Понятие производной функции в точке
Производная и дифференциал Понятие производной функции в точке
 Производная и дифференциал Понятие производной функции в точке Производная степенной функции: любой радикал (корень) нужно представить в виде для применения формулы Свойства степени
Производная и дифференциал Понятие производной функции в точке Производная степенной функции: любой радикал (корень) нужно представить в виде для применения формулы Свойства степени
 Свойства степени
Свойства степени
 Производная и дифференциал Понятие производной функции в точке Производная тригонометрических функций у = sin x Используем формулу двойного угла sin2 = 2 sin* cos и организуем первый замечательный предел
Производная и дифференциал Понятие производной функции в точке Производная тригонометрических функций у = sin x Используем формулу двойного угла sin2 = 2 sin* cos и организуем первый замечательный предел
 Производная и дифференциал Понятие производной функции в точке
Производная и дифференциал Понятие производной функции в точке
 Производная и дифференциал Понятие производной функции в точке Производная логарифмических функций у = ln x Используем свойства логарифма и организуем второй замечательный предел
Производная и дифференциал Понятие производной функции в точке Производная логарифмических функций у = ln x Используем свойства логарифма и организуем второй замечательный предел
 Производная и дифференциал Понятие производной функции в точке
Производная и дифференциал Понятие производной функции в точке
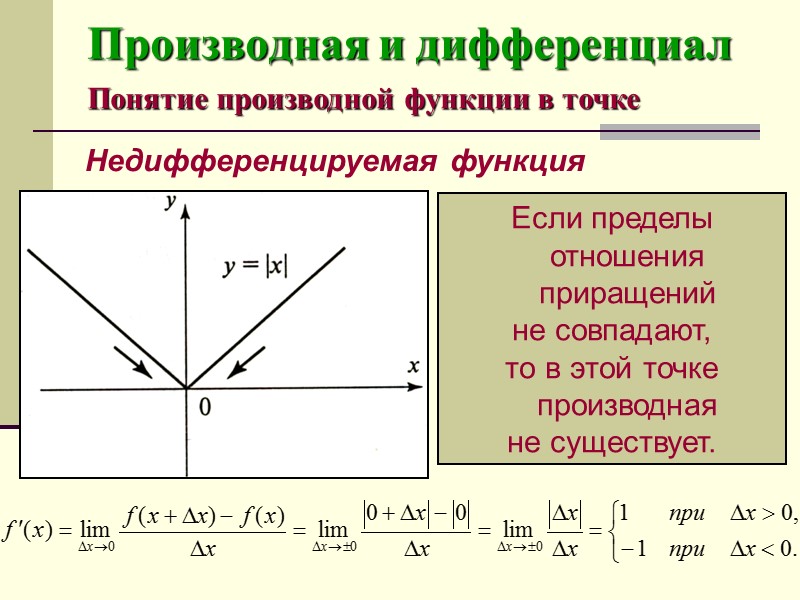
 Производная и дифференциал Понятие производной функции в точке Недифференцируемая функция Если пределы отношения приращений не совпадают, то в этой точке производная не существует.
Производная и дифференциал Понятие производной функции в точке Недифференцируемая функция Если пределы отношения приращений не совпадают, то в этой точке производная не существует.
 Производная и дифференциал Понятие производной функции в точке Следовательно: если функция прерывна, или имеет изломы в заданной точке (хотя и непрерывна), то она недифференцируема в этой точке; если функция имеет производную в точке, то она непрерывна в этой точке.
Производная и дифференциал Понятие производной функции в точке Следовательно: если функция прерывна, или имеет изломы в заданной точке (хотя и непрерывна), то она недифференцируема в этой точке; если функция имеет производную в точке, то она непрерывна в этой точке.
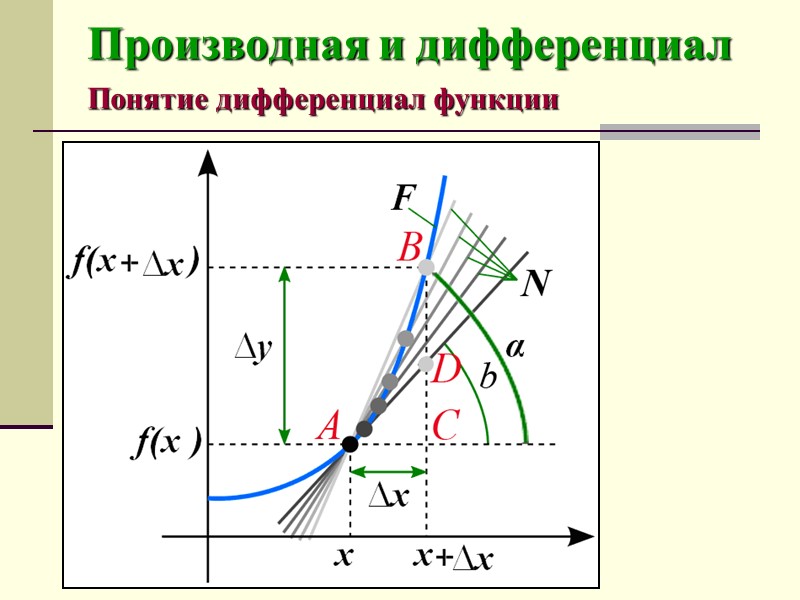
 Производная и дифференциал Понятие дифференциал функции
Производная и дифференциал Понятие дифференциал функции
 Производная и дифференциал Понятие дифференциал функции Δ f f(х)*Δх. Правую часть этого приближенного неравенства называют дифференциалом функции f(х) в точке х и обозначают df(x). df(x)= f(x)*dx
Производная и дифференциал Понятие дифференциал функции Δ f f(х)*Δх. Правую часть этого приближенного неравенства называют дифференциалом функции f(х) в точке х и обозначают df(x). df(x)= f(x)*dx
 Производная и дифференциал Основные правила дифференцирования
Производная и дифференциал Основные правила дифференцирования
 Производная и дифференциал Основные правила дифференцирования Вынесение константы за знак производной Пример. Вычислить производную функции
Производная и дифференциал Основные правила дифференцирования Вынесение константы за знак производной Пример. Вычислить производную функции
 Производная и дифференциал Основные правила дифференцирования Производная суммы функций Пример. Вычислить производную функции
Производная и дифференциал Основные правила дифференцирования Производная суммы функций Пример. Вычислить производную функции
 Производная и дифференциал Основные правила дифференцирования
Производная и дифференциал Основные правила дифференцирования
 Производная и дифференциал Основные правила дифференцирования Производная произведения функций Пример. Вычислить производную функции
Производная и дифференциал Основные правила дифференцирования Производная произведения функций Пример. Вычислить производную функции
 Производная и дифференциал Основные правила дифференцирования
Производная и дифференциал Основные правила дифференцирования
 Производная и дифференциал Основные правила дифференцирования Производная частного функций Пример. Вычислить производную функции
Производная и дифференциал Основные правила дифференцирования Производная частного функций Пример. Вычислить производную функции
 Производная и дифференциал Основные правила дифференцирования
Производная и дифференциал Основные правила дифференцирования
 Производная и дифференциал Основные правила дифференцирования Производная сложной функций Пример 1. Вычислить производную функции Определяем внешнюю и внутреннюю (вложенную) функцию: Применяем правило дифференцирования сложной функции:
Производная и дифференциал Основные правила дифференцирования Производная сложной функций Пример 1. Вычислить производную функции Определяем внешнюю и внутреннюю (вложенную) функцию: Применяем правило дифференцирования сложной функции:
 Производная и дифференциал Основные правила дифференцирования Пример 1. Вычислить производную функции Определяем внешнюю и внутреннюю (вложенную) функцию: Применяем правило дифференцирования степенной функции: Применяем правило дифференцирования сложной функции:
Производная и дифференциал Основные правила дифференцирования Пример 1. Вычислить производную функции Определяем внешнюю и внутреннюю (вложенную) функцию: Применяем правило дифференцирования степенной функции: Применяем правило дифференцирования сложной функции:
 Производная и дифференциал Основные правила вычисления дифференциалов df(x)= f(x)*dx Пример. Вычислить дифференциал функции
Производная и дифференциал Основные правила вычисления дифференциалов df(x)= f(x)*dx Пример. Вычислить дифференциал функции
