Проекции прямой Лекция 2 Положение прямой m

Проекции прямой Лекция

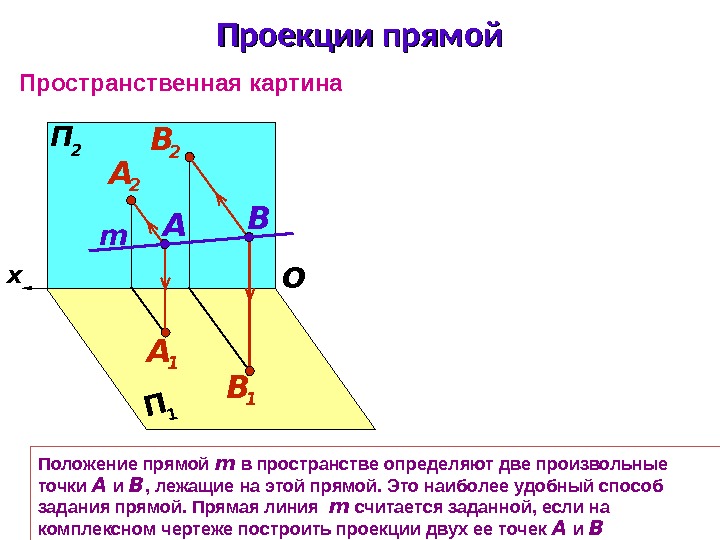
Положение прямой m в пространстве определяют две произвольные точки А и В , лежащие на этой прямой. Это наиболее удобный способ задания прямой. Прямая линия m считается заданной, если на комплексном чертеже построить проекции двух ее точек А и В x П 2 П 1 OПространственная картина Проекции прямой А 2 В 2 А 1 B 1 A B m

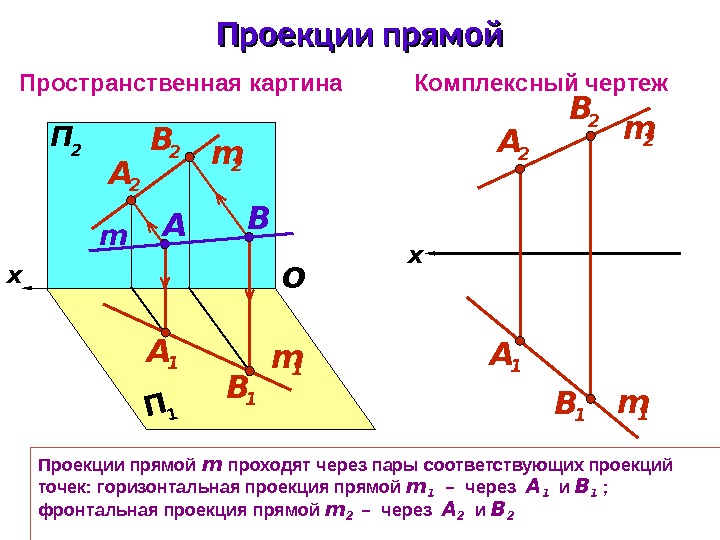
m 2 m 1 x Проекции прямой m проходят через пары соответствующих проекций точек: горизонтальная проекция прямой m 1 – через А 1 и В 1 ; фронтальная проекция прямой m 2 – через А 2 и В 2 x А 2 А 1 B 2 B 1 Пространственная картина Комплексный чертеж Проекции прямой П 2 П 1 OAА 2 А 1 B B 1 m В 2 m

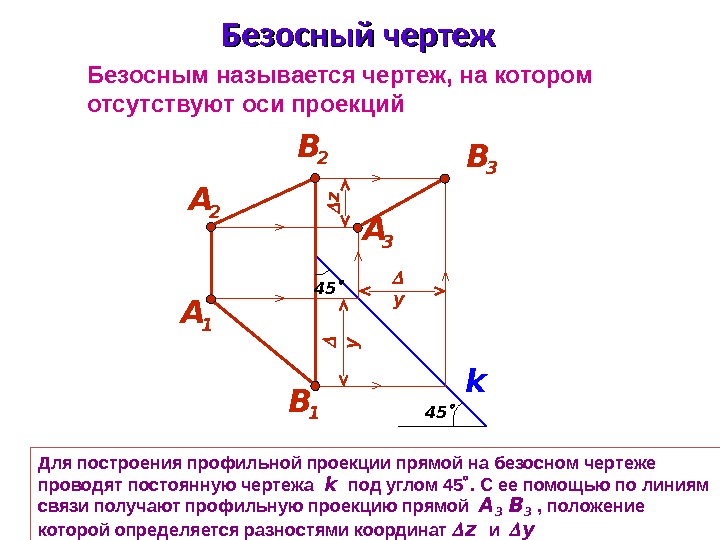
Для построения профильной проекции прямой на безосном чертеже проводят постоянную чертежа k под углом 45 . С ее помощью по линиям связи получают профильную проекцию прямой А 3 В 3 , положение которой определяется разностями координат z и y k B 3 А 3 45 Безосным называется чертеж, на котором отсутствуют оси проекций А 2 А 1 B 2 Безосный чертеж 45 y y z

П 1 x П 2 П 3 Метрические характеристики отрезка: н. в. – натуральная величина отрезка; – угол наклона отрезка к пло c кости П 1 ; – угол наклона отрезка к пло c кости П 2 ; – угол наклона отрезка к пло c кости П 3 А 2 B B 1 В 2 А 1 A В 3 А 3 Положение прямой относительно плоскостей проекций Н. в. z y

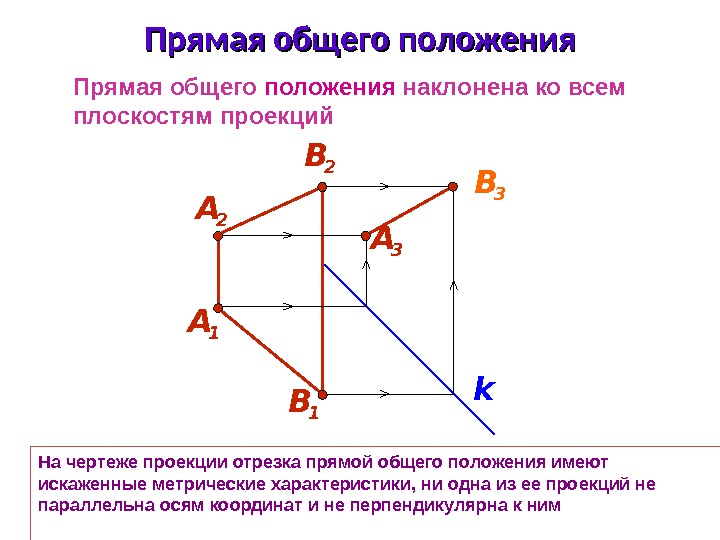
На чертеже проекции отрезка прямой общего положения имеют искаженные метрические характеристики, ни одна из ее проекций не параллельна осям координат и не перпендикулярна к ним Прямая общего положения наклонена ко всем плоскостям проекций Прямая общего положения А 2 А 1 B 2 B 1 B 3 k. А

У прямой частного положения на комплексном чертеже определяются натуральные величины каких-либо ее характеристик. Прямая уровня про-ецируется без искажения на ту плоскость проекций, которой она парал-лельна. Одна из проекций проецирующей прямой вырождается в точку Прямая частного положения параллельна или перпендикулярна одной из плоскостей проекций Прямая, параллельная одной из плоскостей проекций, называется прямой уровня: Горизонтальная прямая уровня (горизонталь) h П 1 Фронтальная прямая уровня (фронталь) f П 2 Профильная прямая p П 3 Прямая, перпендикулярная одной из плоскостей проекций, называется проецирующей прямой: Горизонтально проецирующая прямая П 1 Фронтально проецирующая прямая П 2 Профильно проецирующая прямая П 3 Прямые частного положения

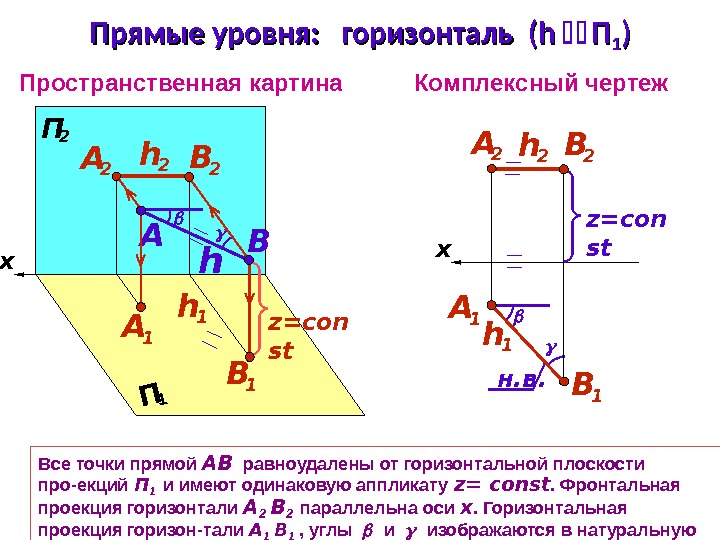
x П 2 П 1 Все точки прямой АВ равноудалены от горизонтальной плоскости про-екций П 1 и имеют одинаковую аппликату z= const. Фронтальная проекция горизонтали А 2 В 2 параллельна оси х. Горизонтальная проекция горизон-тали А 1 В 1 , углы и изображаются в натуральную величину на П 1 Пространственная картина Комплексный чертеж x z = con st h BA z = con st. Прямые уровня: горизонталь (( h h ПП 11 )) h 1 B 1 А 1 н. в. А 2 В 2 h 2 B 1 А 1 h

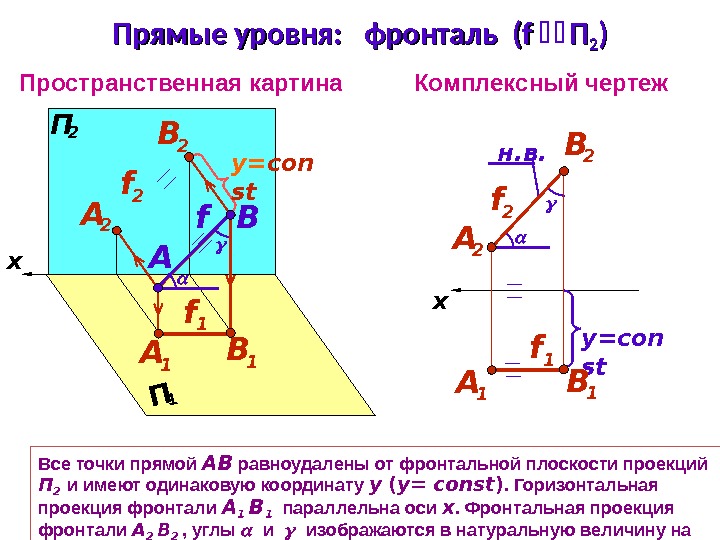
Пространственная картина Комплексный чертежx y = con st П 1 x П 2 By = con st н. в. f. Прямые уровня: фронталь (( f f ПП 22 )) A B 1 А 1 f 1 А 2 В 2 f 2 B 1 А 1 Все точки прямой АВ равноудалены от фронтальной плоскости проекций П 2 и имеют одинаковую координату y ( y= const ). Горизонтальная проекция фронтали А 1 В 1 параллельна оси х. Фронтальная проекция фронтали А 2 В 2 , углы и изображаются в натуральную величину на П

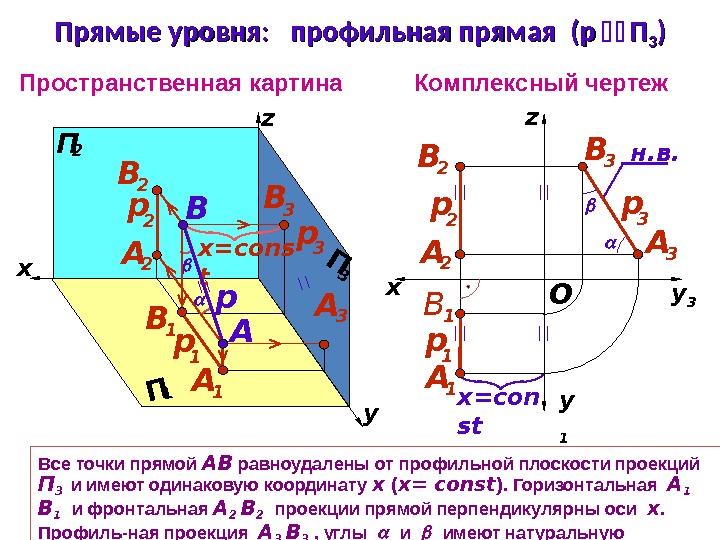
Все точки прямой АВ равноудалены от профильной плоскости проекций П 3 и имеют одинаковую координату х ( х = const ). Горизонтальная А 1 В 1 и фронтальная А 2 В 2 проекции прямой перпендикулярны оси х. Профиль-ная проекция А 3 В 3 , углы и имеют натуральную величину на П 3 Пространственная картина Комплексный чертеж z Ox y 1 y 3 x = con st П 1 x П 2 П 3 B A н. в. В 3 рx = cons t. Прямые уровня: профильная прямая (р(р ПП 33 )) А 2 В 2 р 2 B 1 А 1 р 1 А 3 р 3 А 1 B 1 р 1 А 2 В 2 р 2 А 3 р 3 В 3 z y

xн. в. Пространственная картина Комплексный чертеж x П 2 A B В 2 А 2 B 1( А ) 1 Горизонтально проецирующая прямая (( ПП 11 )) А 2 В 2 1 B 1( А ) П 1 Прямая перпендикулярна П 1 , поэтому ее горизонтальная проекция А 1 В 1 вырождается в точку. Относительно П 2 и П 3 прямая параллельна и изображается на этих плоскостях проекций в натуральную величину. Проекция А 2 В 2 перпендикулярна оси координат х

Прямая перпендикулярна фронтальной плоскости проекций П 2 и парал-лельна П 1 и П 3 . Фронтальная проекция А 2 В 2 вырождается в точку. На П 1 и П 3 прямая проецируется в натуральную величину. Проекция А 1 В 1 перпендикулярна оси координат х. Пространственная картина Комплексный чертеж x П 2 П 1 AB x н. в. B 1 А 1 А 2(В ) 2 Фронтально проецирующая прямая (( ПП 22 )) А 2(В ) 2 B 1 А

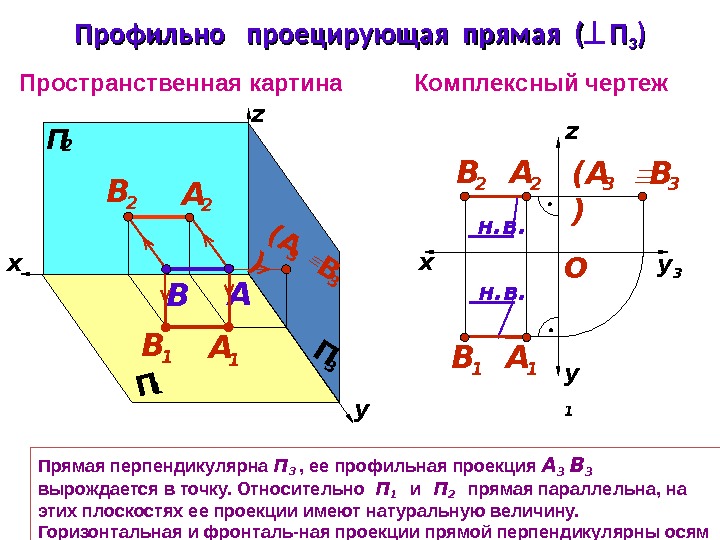
Прямая перпендикулярна П 3 , ее профильная проекция А 3 В 3 вырождается в точку. Относительно П 1 и П 2 прямая параллельна, на этих плоскостях ее проекции имеют натуральную величину. Горизонтальная и фронталь-ная проекции прямой перпендикулярны осям y и z , соответственно. Пространственная картина Комплексный чертеж. П 1 x П 2 П 3 B A x z y 1 y 3 н. в. Профильно проецирующая прямая (( ПП 33 )) B 1 А 1 B 3( A ) 3 OB 2 А 1 B 1 А 2 В 2 (А )3 В 3 z y

Преобразование чертежа прямой общего положения.

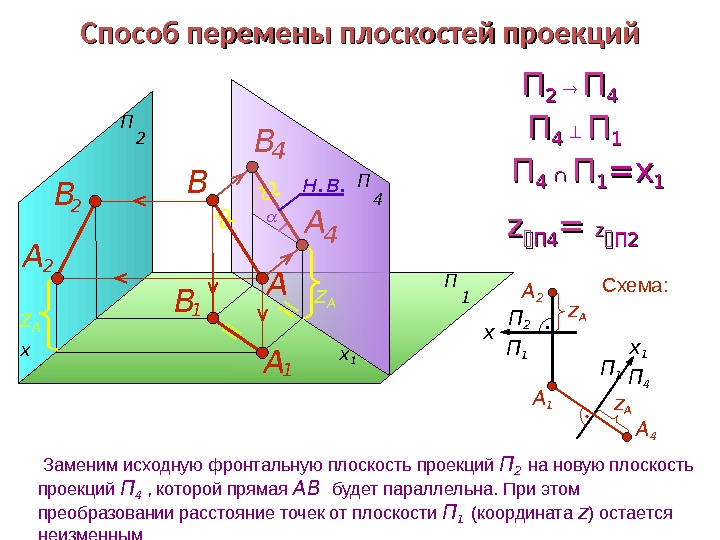
П 2 П 1 x П 4 x 1 АВ Заменим исходную фронтальную плоскость проекций П 2 на новую плоскость проекций П 4 , которой прямая АВ будет параллельна. При этом преобразовании расстояние точек от плоскости П 1 (координата z ) остается неизменным П 1 П 4 x 1 А 4 z А z АСпособ перемены плоскостей проекций z А А 4 В 4 АВ н. в. В 1 А 1 В 2 А 2 Схема: ПП 2 2 ПП 44 zz П 4 П 4 = = zz П 2 П 2 ПП 4 4 ПП 1 1 ПП 4 4 ПП 11 == xx 11 П 1 П 2 А 1 А 2 x

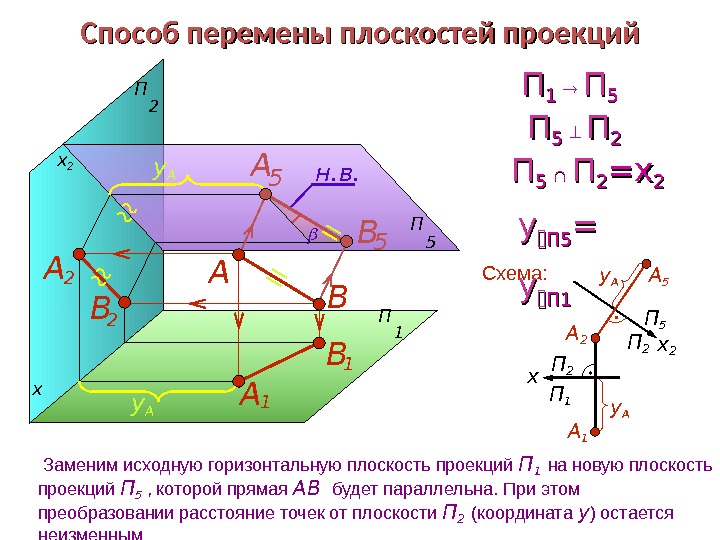
x 2 П 2 П 5 Способ перемены плоскостей проекций П 2 П 1 П 5 x x 2 В 2 А 2 В 1 А 1 н. в. y А А 5 ВА Схема: ПП 1 1 ПП 55 yy ПП 55 = = yy ПП 11 ПП 5 5 ПП 2 2 ПП 5 5 ПП 22 == xx 22 А 5 y А y АП 1 П 2 А 1 А 2 x Заменим исходную горизонтальную плоскость проекций П 1 на новую плоскость проекций П 5 , которой прямая АВ будет параллельна. При этом преобразовании расстояние точек от плоскости П 2 (координата у ) остается неизменным

П 1 x П 2 А 1 B 1 А 2 B 2 Определение н. в. отрезка и его углов наклона к плоскостям проекций (способ замены плоскостей проекций) Ось х 1 новой плоскости проекций П 4 проведем параллельно горизон-тальной проекции отрезка А 1 В 1 . В этом преобразовании сохраняются z — координаты точек. На П 4 определяются натуральная величина отрезка и его угол наклона к плоскости проекций П 1 x 1 П 4 П 1 А 4 В 4 н. в. Схема: П 1 П 4 x 1 А 4 z А z АП 1 П 2 А 1 А 2 x

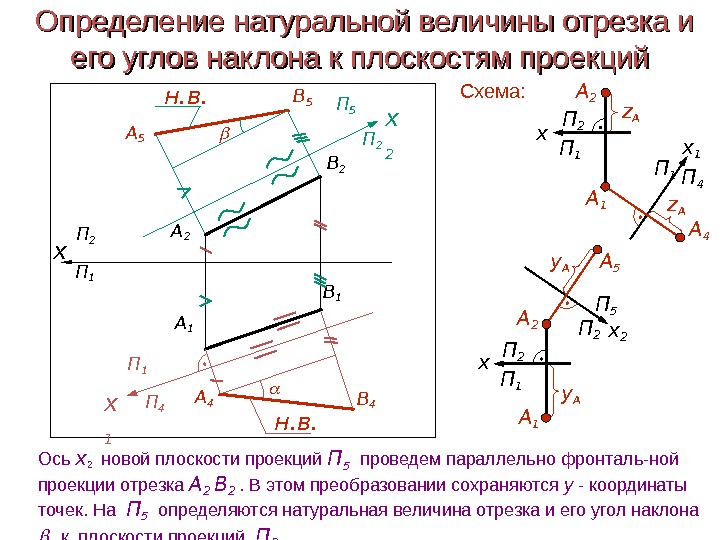
Определение натуральной величины отрезка и его углов наклона к плоскостям проекций x 2 П 2 П 5 А 5 y А y АП 1 П 2 А 1 А 2 xx А 1 B 1 А 2 B 2 П 1 x 1 П 4 П 1 А 4 В 4 н. в. x 2 П 2 П 5 А 5 В 5 н. в. Схема: П 1 П 4 x 1 А 4 z А z АП 1 П 2 А 1 А 2 x Ось х 2 новой плоскости проекций П 5 проведем параллельно фронталь-ной проекции отрезка А 2 В 2 . В этом преобразовании сохраняются y — координаты точек. На П 5 определяются натуральная величина отрезка и его угол наклона к плоскости проекций П

x. А 1 B 1 А 2 В 2 l 2 A 1 A 2 н. в. l 1 Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Схема: А 1 А 2 П 1 П 2 x А 1 А 2 i 1 i 2 Для упрощения горизонтально-проецирующую ось вращения l проводят через точку В , которая остается неподвижной. Точка А 1 описывает дугу окружности с центром в точке l 1 так, чтобы В 1 А 1 оси х. Тогда прямая АВ займет положение фронтали. На П 2 угол и отрезок АВ не искажаются

x н. в. l 2 А 1 B 1 А 2 В 2 A 1 A 2 н. в. i 1 B 2 i 2 B 1 l 1 Схема: А 1 А 2 П 1 П 2 x А 1 А 2 i 1 i 2 А 1 А 2 П 1 П 2 А 1 А 2 x i 1 i 2 Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Для определения угла прямую АВ нужно вращать вокруг оси i П 2 до положения горизонтали. Ось проходит через точку А , которая неподвижна. Точка В 2 вращается по дуге окружности с центром в точке i 2 до положения В 2 А 2 оси х. На П 1 угол и отрезок АВ не искажаются

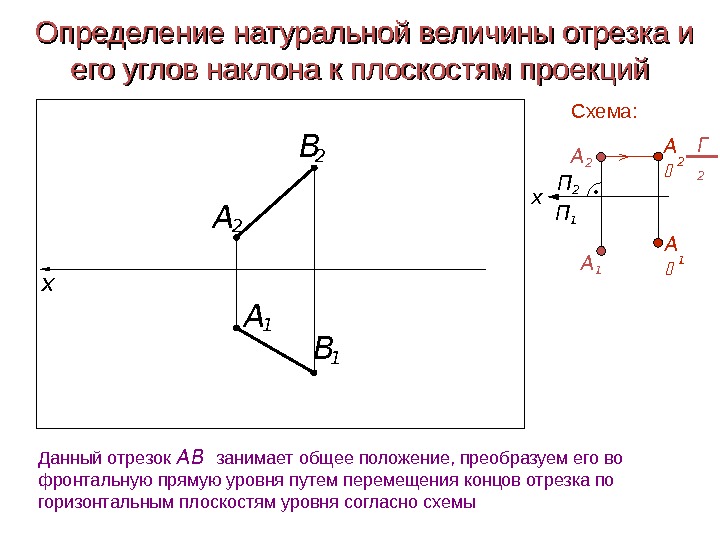
x. А 1 B 1 А 2 В 2 Определение натуральной величины отрезка и его углов наклона к плоскостям проекций Данный отрезок АВ занимает общее положение, преобразуем его во фронтальную прямую уровня путем перемещения концов отрезка по горизонтальным плоскостям уровня согласно схемы А 1 А 2 А 1 П 1 П 2 А 2 x Схема: Г

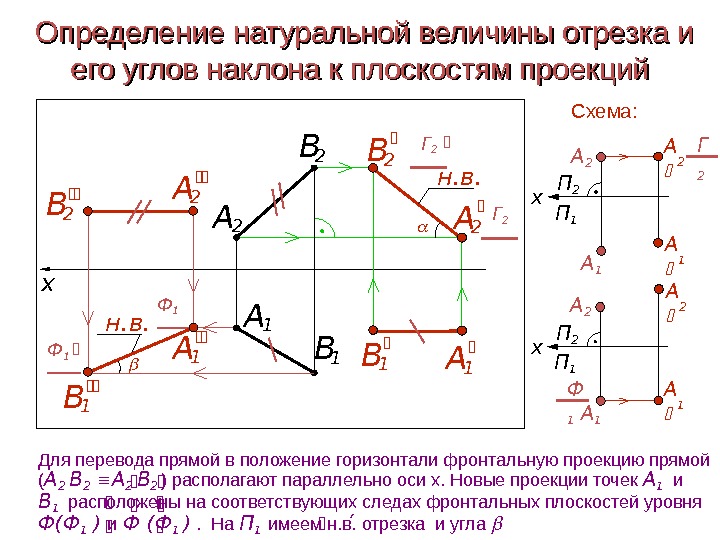
Определение натуральной величины отрезка и его углов наклона к плоскостям проекцийx н. в. A 2 B 2 A 1 В 1 А 1 B 1 А 2 В 2 А 1 А 2 А 1 П 1 П 2 А 2 x Схема: Г 2 Г 2 Горизонтальную проекцию прямой ( А 1 В 1 ) располагают параллель-но оси х. Фронтальную проекцию (определяющую н. в. отрезка и угла ) задают новые проекции точек А 2 и В 2 , расположенные на соответствую-щих следах горизонтальных плоскостей уровня Г(Г 2 ) и Г(Г 2 )

Определение натуральной величины отрезка и его углов наклона к плоскостям проекций н. в. A 1 x. А 1 B 1 А 2 В 2 A 2 н. в. B 2 В 1 А 1 А 2 А 1 П 1 П 2 А 2 x Схема: Г 2 А 1 А 1 П 1 П 2 А 2 x Ф 1 А 2 B 2 Ф 1 B 1 А 1 Г 2 Г 2 Для перевода прямой в положение горизонтали фронтальную проекцию прямой ( А 2 В 2 ) располагают параллельно оси х. Новые проекции точек А 1 и В 1 расположены на соответствующих следах фронтальных плоскостей уровня Ф(Ф 1 ) и Ф (Ф 1 ) . На П 1 имеем н. в. отрезка и угла

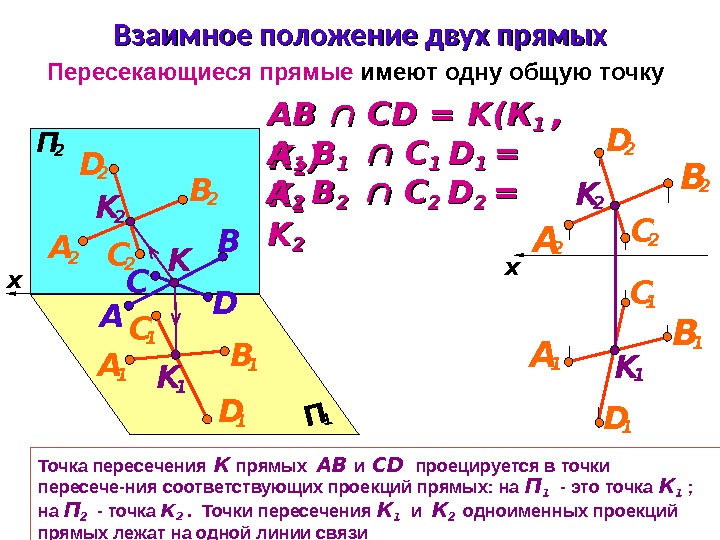
x. П 1 П 2 Взаимное положение двух прямых Пересекающиеся прямые имеют одну общую точку B A B 1 А 1 А 2 В 2 DC D 1 D 2 C 2 K C 1 K 1 K 2 x А 1 А 2 В 2 B 1 D 2 C 1 D 1 K 2 K 1 АВАВ С С D D = = KK (К(К 1 1 , , КК 22 ))АА 1 1 ВВ 11 С С 1 1 DD 1 1 = = KK 11 АА 22 ВВ 22 С С 22 DD 22 = = KK 22 Точка пересечения К прямых АВ и С D проецируется в точки пересече-ния соответствующих проекций прямых: на П 1 — это точка К 1 ; на П 2 — точка К 2 . Точки пересечения К 1 и К 2 одноименных проекций прямых лежат на одной линии связи

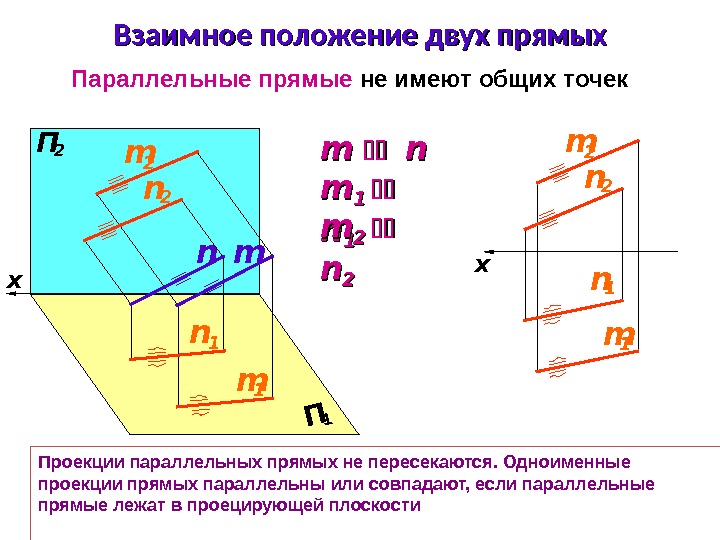
x. П 1 П 2 Взаимное положение двух прямых Параллельные прямые не имеют общих точек Проекции параллельных прямых не пересекаются. Одноименные проекции прямых параллельны или совпадают, если параллельные прямые лежат в проецирующей плоскости n m m 1 n 1 m 2 n 2 x m 2 n 1 n 2 m 1 m m nn mm 1 1 nn 1 1 mm 22 nn

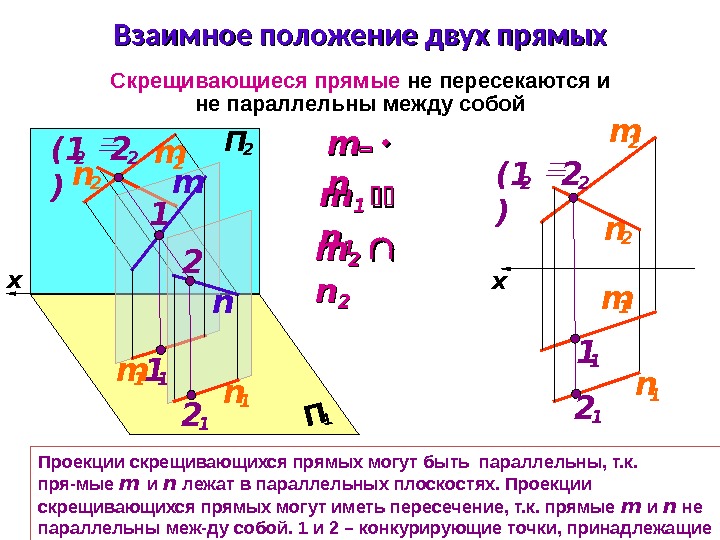
x Взаимное положение двух прямых Скрещивающиеся прямые не пересекаются и не параллельны между собой Проекции скрещивающихся прямых могут быть параллельны, т. к. пря-мые m и n лежат в параллельных плоскостях. Проекции скрещивающихся прямых могут иметь пересечение, т. к. прямые m и n не параллельны меж — ду собой. 1 и 2 – конкурирующие точки, принадлежащие разным прямым. П 1 П 2 m 1 m 2 n 2 m n mm 1 1 nn 1 1 mm 22 nn 22 m m nn m 1 x n 1 m 2 n 2 1 1 2 2(1 ) 2 n 12 1 1 2 11 2(1 )

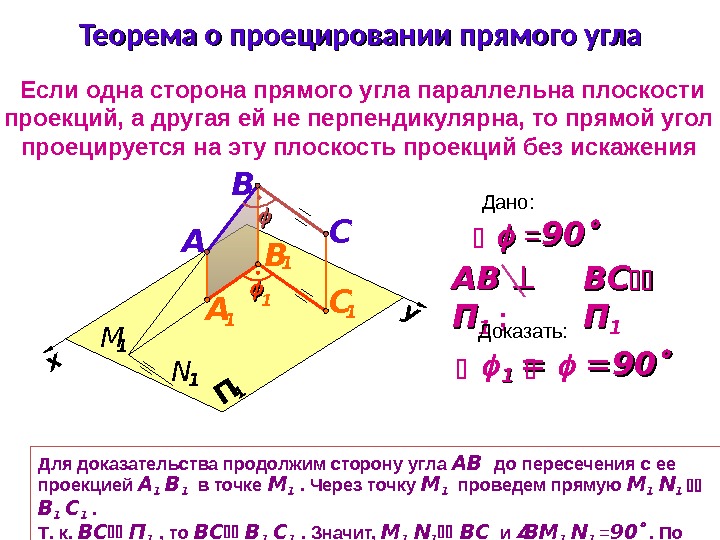
Теорема о проецировании прямого угла Если одна сторона прямого угла параллельна плоскости проекций, а другая ей не перпендикулярна, то прямой угол проецируется на эту плоскость проекций без искажения Для доказательства продолжим сторону угла АВ до пересечения с ее проекцией А 1 В 1 в точке М 1 . Через точку М 1 проведем прямую М 1 N 1 В 1 C 1 . Т. к. BC П 1 , то BC В 1 С 1 . Значит, М 1 N 1 ВС и BM 1 N 1 = 90 . По теореме о 3 -х перпендикулярах B 1 M 1 N 1 = 90 , следовательно, и A 1 В 1 С 1 = 90 BCBC ПП 1 АВ АВ ПП 1 ; B x П 1 y A B 1 А 1 C C 1 М 1 N 1 1 == 9090 1 1 = = == 9090 Дано: Доказать:

b 2 Теорема о проецировании прямого угла b 1 h 2 h 1 x н. в. Если на чертеже есть изображение прямого угла, то одна из его сторон обязательно натуральная величинаb hb h = = 9090 Дано:

xf 1 f 2 С 1 C 2 D 1 Теорема о проецировании прямого угла н. в. Задача: Построить проекции перпендикуляра, проведенного из точки С к прямой f D 2 DD 22 DD 1 CC 22 DD 22 ff 2 DD 11 CC 1 Прямая f является фронталью и проецируется на П 2 в натуральную величину. Следовательно, фронтальная проекция перпендикуляра С 2 D 2 перпендикулярна фронтальной проекции прямой f . Определяем основа-ние перпендикуляра – точку D. Строим горизонтальную проекцию С

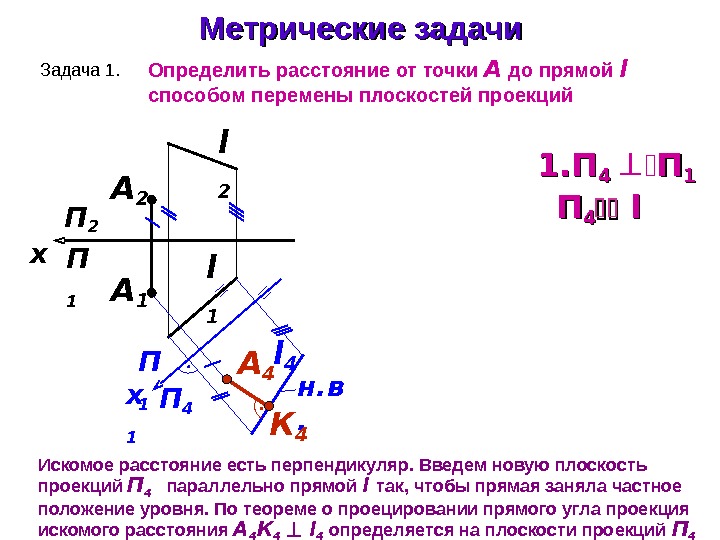
Метрические задачи Задача 1. Определить расстояние от точки А до прямой l способом перемены плоскостей проекций П 1 П 2 x l 2 А 1 l 1 А 2 l 4 А 4 н. в. П 1 П 4 x 1 К 4 Искомое расстояние есть перпендикуляр. Введем новую плоскость проекций П 4 параллельно прямой l так, чтобы прямая заняла частное положение уровня. По теореме о проецировании прямого угла проекция искомого расстояния А 4 К 4 l 4 определяется на плоскости проекций П 41. 1. ПП 44 ПП 11 ПП 44 ll

Метрические задачи Задача 1. Определить расстояние от точки А до прямой l способом перемены плоскостей проекций П 1 П 2 x l 2 А 1 l 1 А 2 П 4 П 5 x 2 l 4 А 4 н. в. П 1 П 4 x 1 К 4 К 1 К 2 l 5 А 5 н. в. К 5 1. 1. ПП 44 ПП 11 ПП 44 ll 2. 2. ПП 55 ПП 44 ПП 5 5 ll АК- искомое расстоя ниение При втором преобразовании введем новую плоскость проекций П 5 перпендикулярно прямой l так, чтобы прямая заняла проецирующее положение. На П 5 определяем натуральную величину А 5 К 5 перпендикуляра АК