Признак перпендикулярност и плоскостей. Определение Две пересекающиеся







pryam_parallelepiped_10.ppt
- Размер: 1.1 Мб
- Автор:
- Количество слайдов: 21
Описание презентации Признак перпендикулярност и плоскостей. Определение Две пересекающиеся по слайдам
 Признак перпендикулярност и плоскостей.
Признак перпендикулярност и плоскостей.
 Определение Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
Определение Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
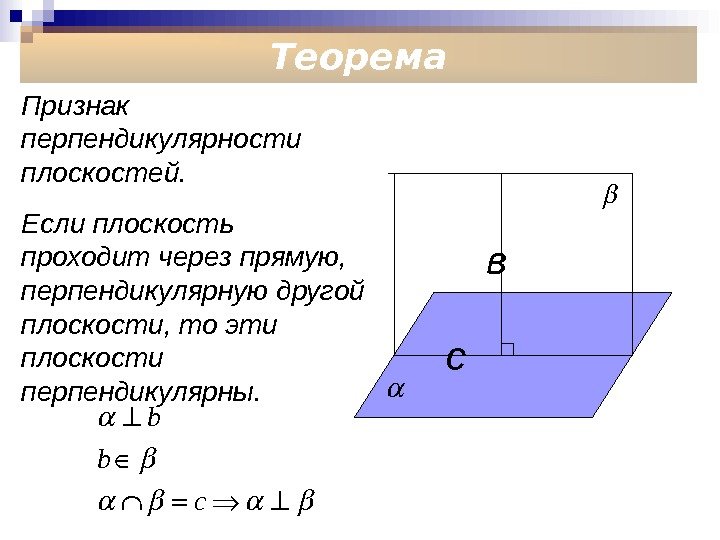
 Теорема Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. с в b b c
Теорема Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. с в b b c
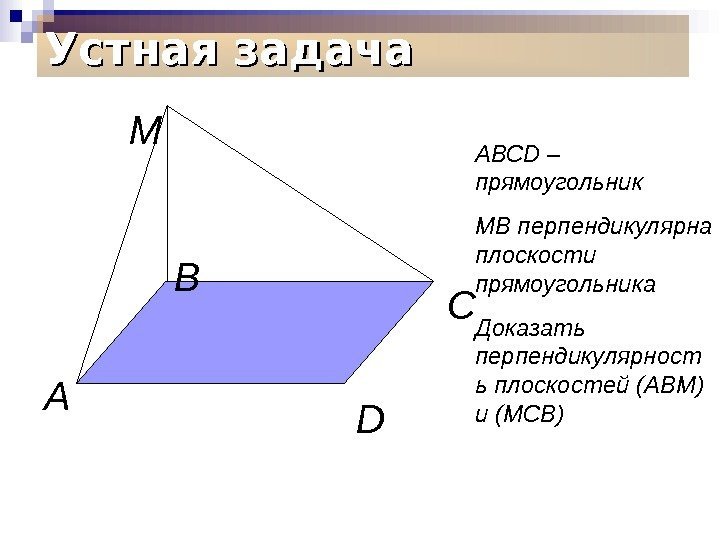
 Устная задача А В С DМ АВС D – прямоугольник МВ перпендикулярна плоскости прямоугольника Доказать перпендикулярност ь плоскостей (АВМ) и (МСВ)
Устная задача А В С DМ АВС D – прямоугольник МВ перпендикулярна плоскости прямоугольника Доказать перпендикулярност ь плоскостей (АВМ) и (МСВ)
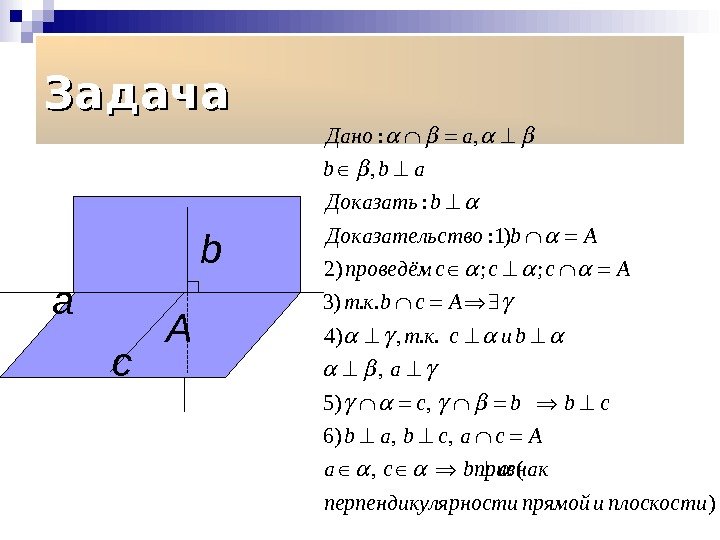
 Задача А b а: , , : : 1) 2) ; ; 3). . 4) , . . , 5) , 6) , , , ( Дано а b b a Доказать b Доказательство b A проведём с с с А т к b c A т к c и b a c b b c b a b c a c A a c bпризнак перпендикулярности прямой и плоскост )и с
Задача А b а: , , : : 1) 2) ; ; 3). . 4) , . . , 5) , 6) , , , ( Дано а b b a Доказать b Доказательство b A проведём с с с А т к b c A т к c и b a c b b c b a b c a c A a c bпризнак перпендикулярности прямой и плоскост )и с

 А В C 1 СD А
А В C 1 СD А
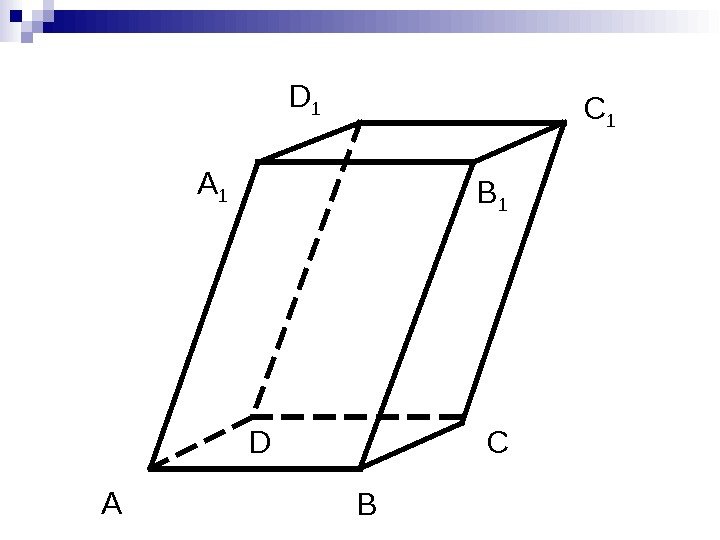
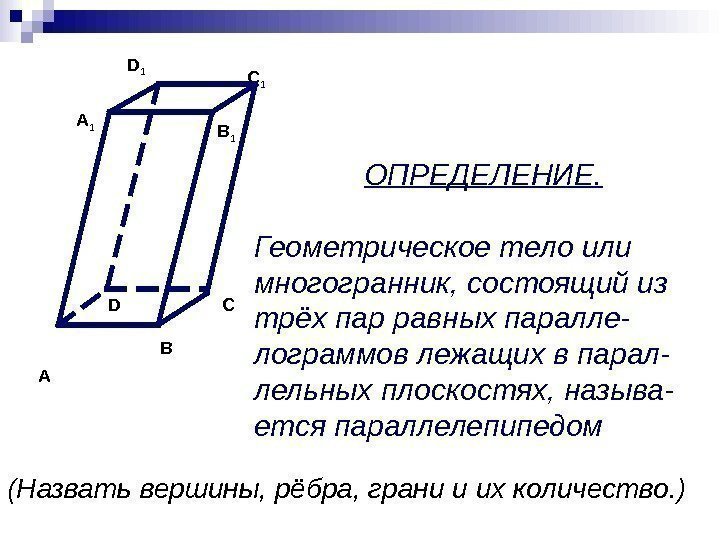
 C 1 А В СD А 1 B 1 D 1 ОПРЕДЕЛЕНИЕ. Геометрическое тело или многогранник, состоящий из трёх пар равных паралле- лограммов лежащих в парал- лельных плоскостях, называ- ется параллелепипедом (Назвать вершины, рёбра, грани и их количество. )
C 1 А В СD А 1 B 1 D 1 ОПРЕДЕЛЕНИЕ. Геометрическое тело или многогранник, состоящий из трёх пар равных паралле- лограммов лежащих в парал- лельных плоскостях, называ- ется параллелепипедом (Назвать вершины, рёбра, грани и их количество. )
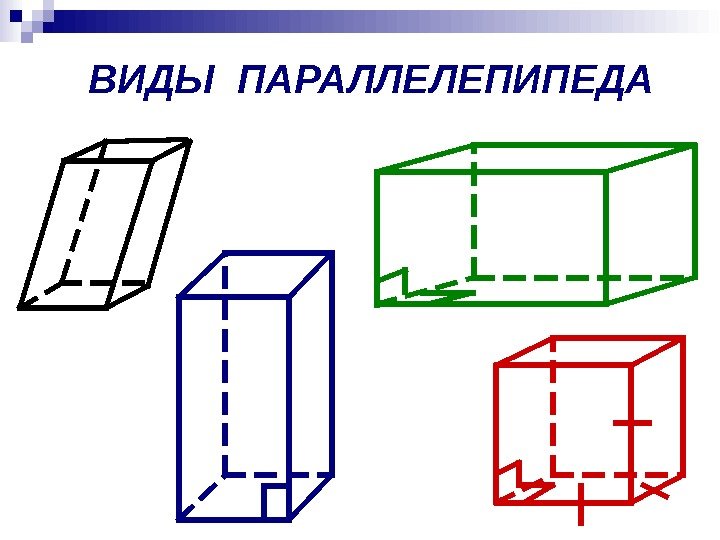
 ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
ВИДЫ ПАРАЛЛЕЛЕПИПЕДА
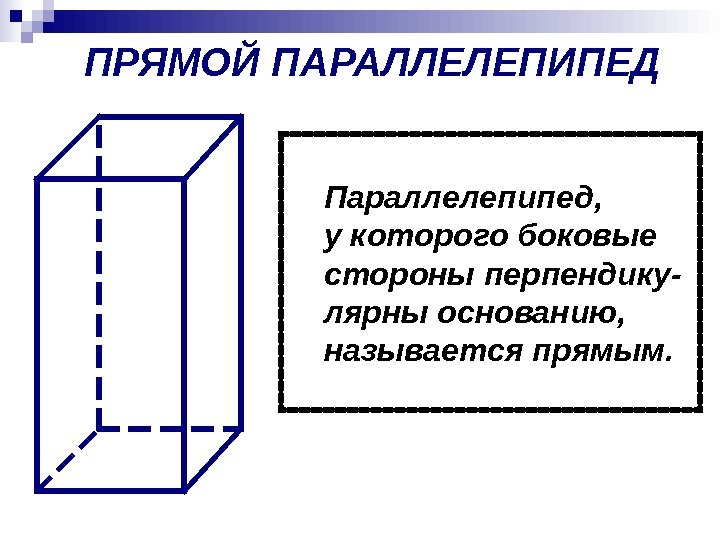
 ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД Параллелепипед, у которого боковые стороны перпендику- лярны основанию, называется прямым.
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД Параллелепипед, у которого боковые стороны перпендику- лярны основанию, называется прямым.
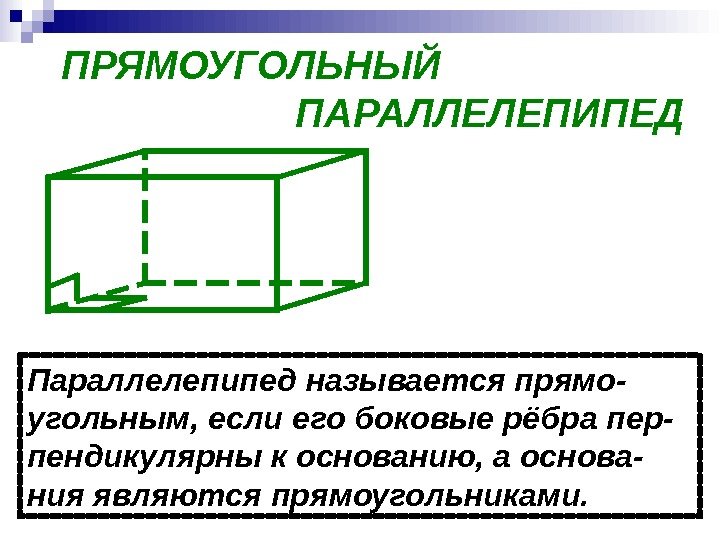
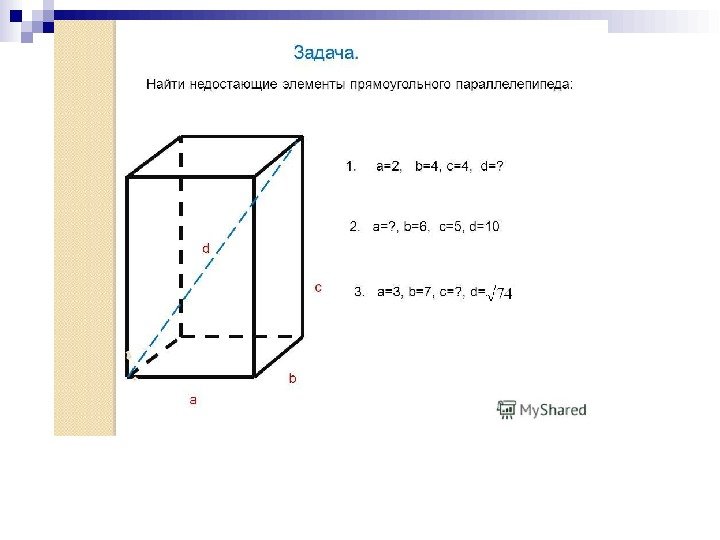
 ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Параллелепипед называется прямо- угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Параллелепипед называется прямо- угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа- ния являются прямоугольниками.
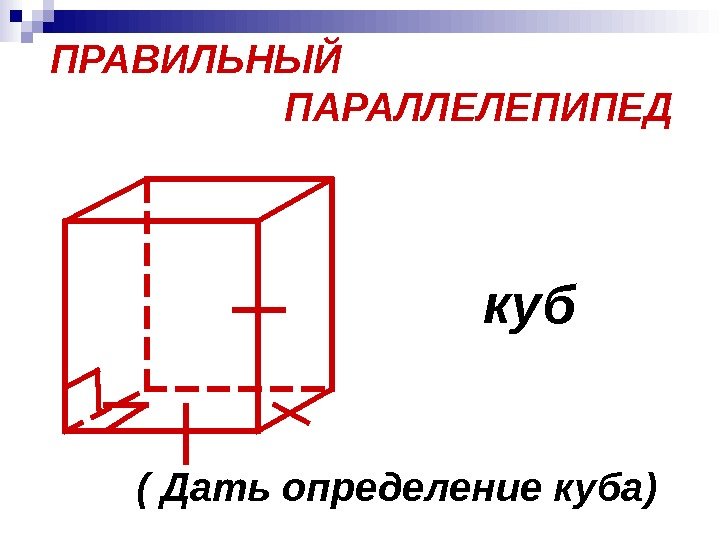
 ПРАВИЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД куб ( Дать определение куба)
ПРАВИЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД куб ( Дать определение куба)
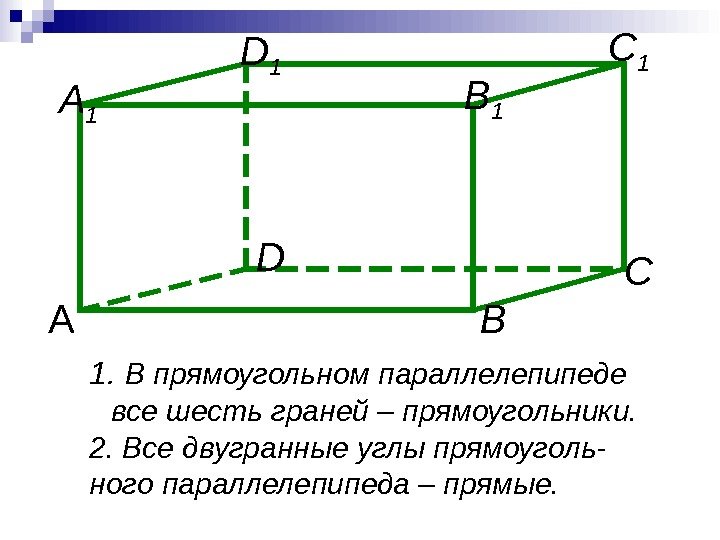
 C 1 А В СDA 1 D 1 B 1 1. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 2. Все двугранные углы прямоуголь- ного параллелепипеда – прямые.
C 1 А В СDA 1 D 1 B 1 1. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 2. Все двугранные углы прямоуголь- ного параллелепипеда – прямые.
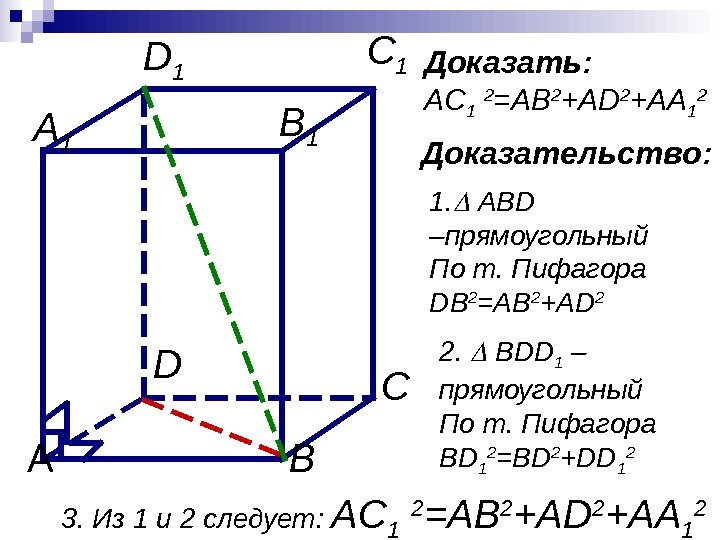
 C 1 А В СDA 1 D 1 B 1 Доказать: AC 1 2 =AB 2 +AD 2 +AA 1 2 Доказательство: 1. ABD – прямоугольный По т. Пифагора DB 2 =AB 2 +AD 2 2. BDD 1 – прямоугольный По т. Пифагора BD 1 2 =BD 2 +DD 1 2 3. Из 1 и 2 следует: AC 1 2 =AB 2 +AD 2 +
C 1 А В СDA 1 D 1 B 1 Доказать: AC 1 2 =AB 2 +AD 2 +AA 1 2 Доказательство: 1. ABD – прямоугольный По т. Пифагора DB 2 =AB 2 +AD 2 2. BDD 1 – прямоугольный По т. Пифагора BD 1 2 =BD 2 +DD 1 2 3. Из 1 и 2 следует: AC 1 2 =AB 2 +AD 2 +

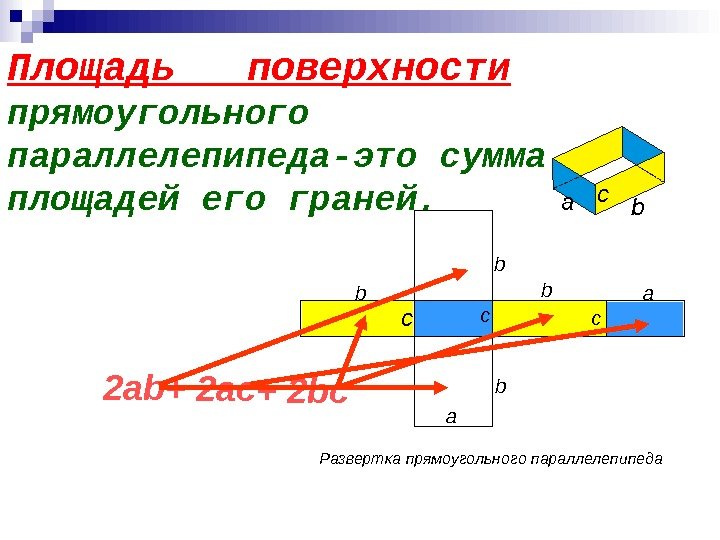
 Площадь поверхности прямоугольного параллелепипеда-это сумма площадей его граней. c a b Развертка прямоугольного параллелепипеда 2 ab + 2 ac + 2 bc c b cb с аb b а
Площадь поверхности прямоугольного параллелепипеда-это сумма площадей его граней. c a b Развертка прямоугольного параллелепипеда 2 ab + 2 ac + 2 bc c b cb с аb b а





