Принцип ієрархії моделей експонентне зростання Томас

Принцип ієрархії моделей

експонентне зростання Томас Роберт Мальтус 1766 -1834 Augustin Louis Cauchy 17 89 -18 57 yxfy, 0, , dyyx. Qdxyx. P tytx

обмежене зростання — Pierre Francois Verhulst 1804 —

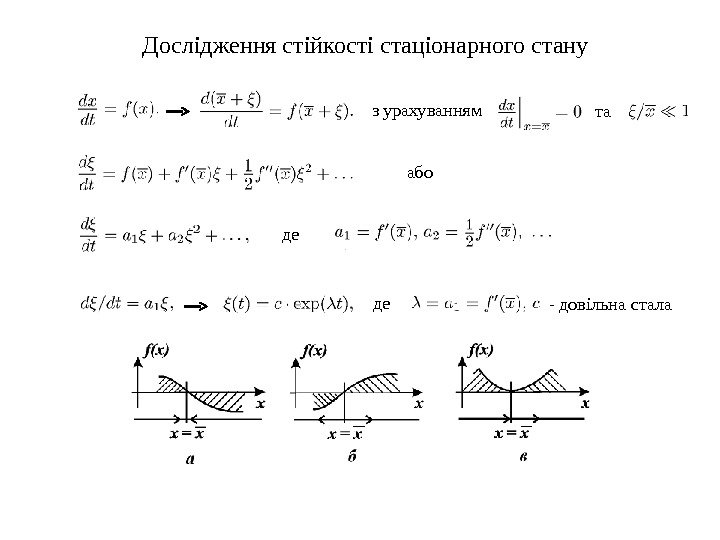
Дослідження стійкості стаціонарного стану з урахуванням та або де де — довільна стала

поповнення

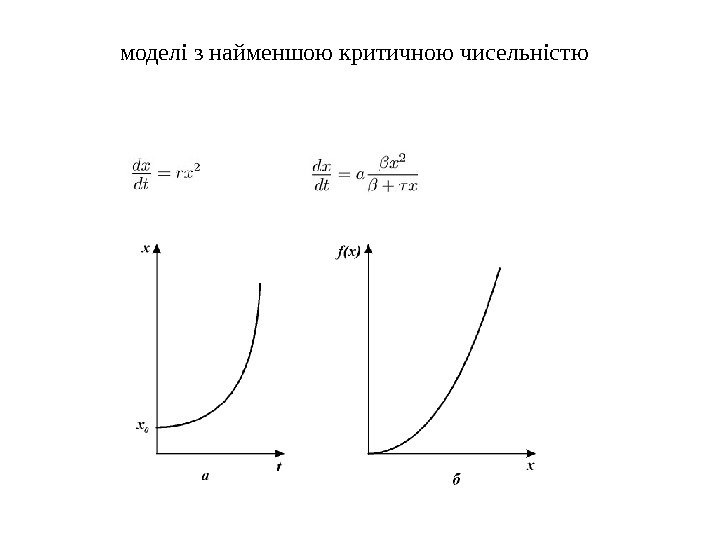
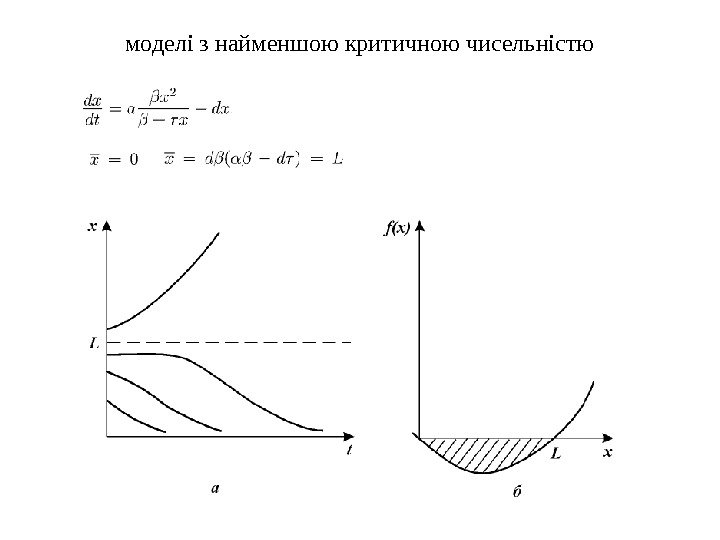
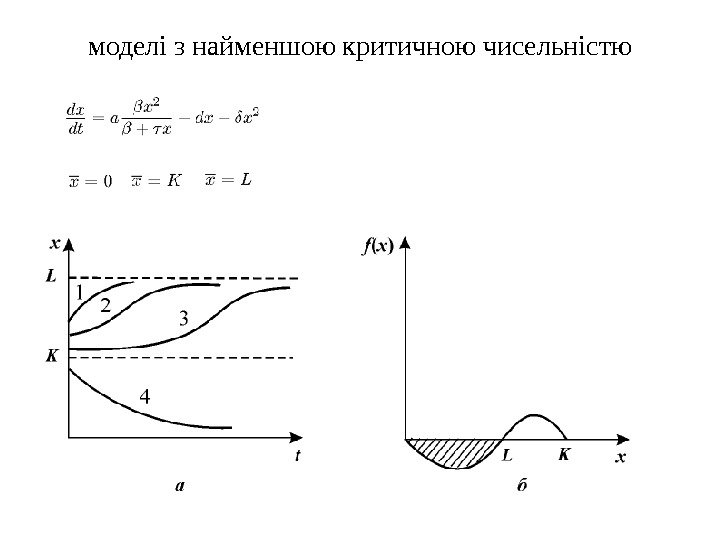
моделі з найменшою критичною чисельністю

моделі з найменшою критичною чисельністю

моделі з найменшою критичною чисельністю

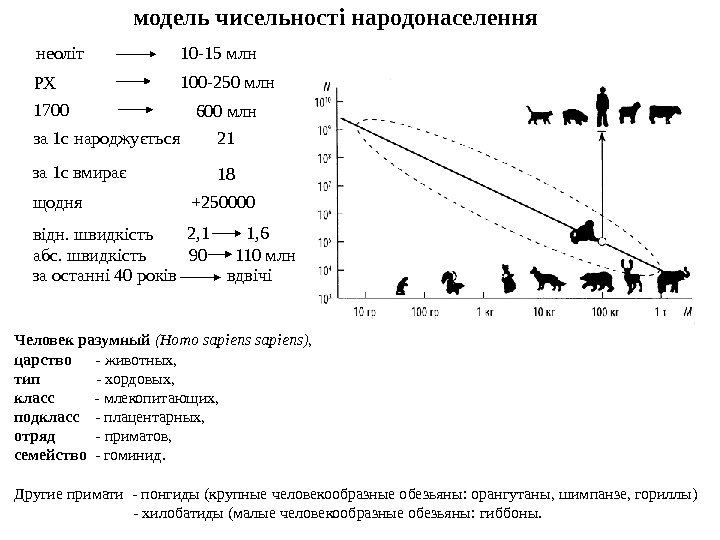
модель чисельності народонаселення

модель чисельності народонаселення 1700 600 млн за 1 с народжується за 1 с вмирає 21 18 щодня +250000 90 110 млнвідн. швидкість 2, 1 1, 6 абс. швидкість за останні 40 років вдвічі неоліт 10 -15 млн РХ 100 -250 млн Человек разумный (Homo sapiens), царств о — животных, тип — хордовых, класс — млекопитающих, подкласс — плацентарных, отряд — приматов, семейств о — гоминид. Другие примат и — понгиды ( крупные человекообразные обезьяны : орангутаны, шимпанзе, гориллы ) — хилобатиды ( малые человекообразные обезьяны : гиббоны.

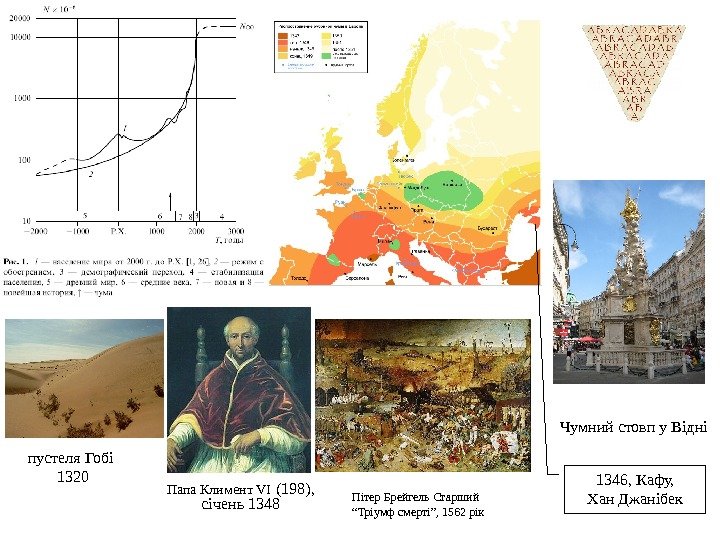
Історична динаміка народонаселення

Чумний стовп у Відні Папа Климент VI (198), січень 1348 пустеля Гобі 1320 Пітер Брейгель Старший “ Тріумф смерті”, 1562 рік 1346, Кафу, Хан Джанібек

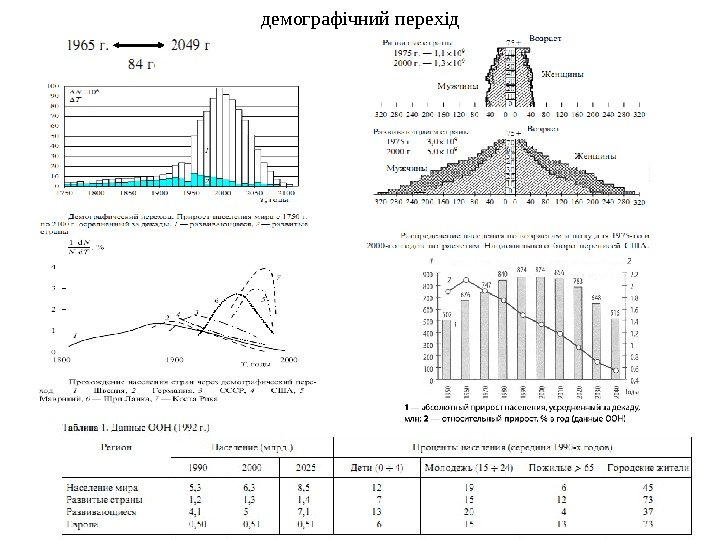
демографічний перехід

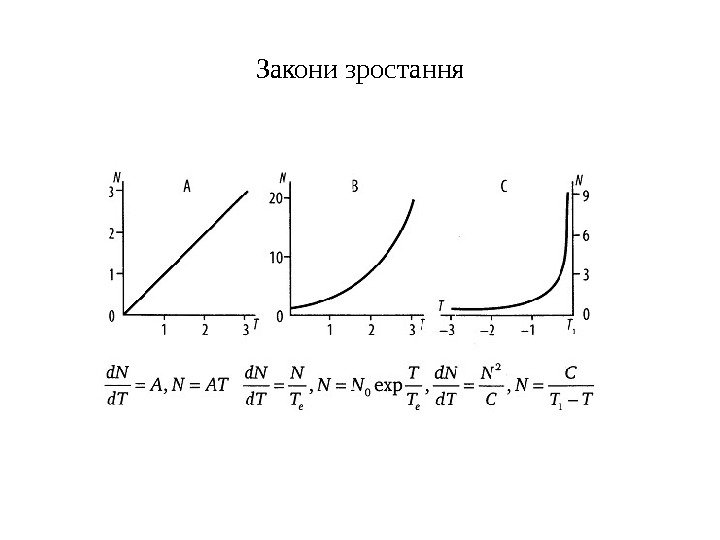
Закони зростання

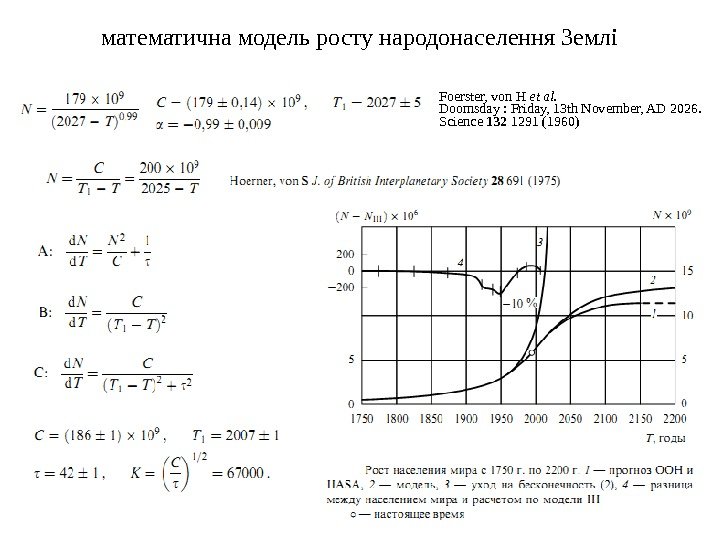
математична модель росту народонаселення Землі Foerster, von H et al. Doomsday : Friday, 13 th November, AD 2026. Science 132 1291 (1960)

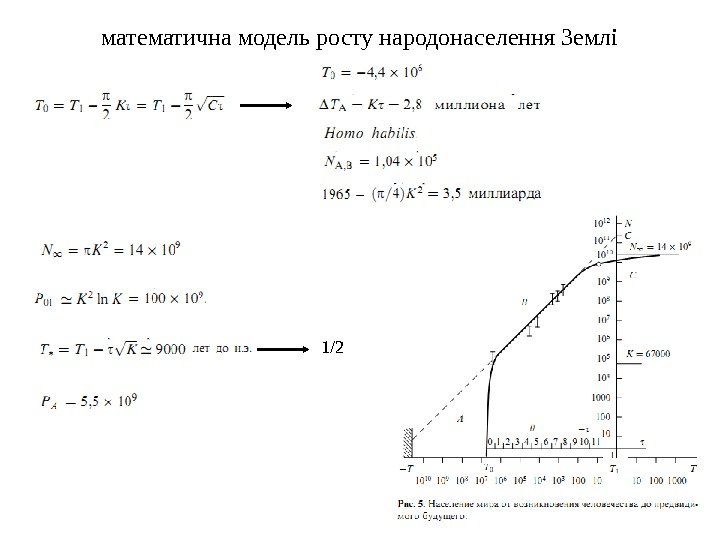
математична модель росту народонаселення Землі 1/

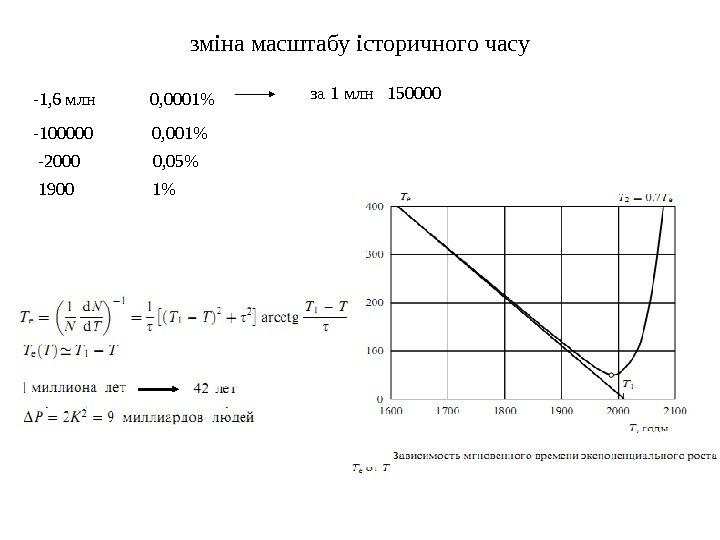
зміна масштабу історичного часу -1, 6 млн 0, 0001% -100000 0, 001% -2000 0, 05% 1900 1% за 1 млн

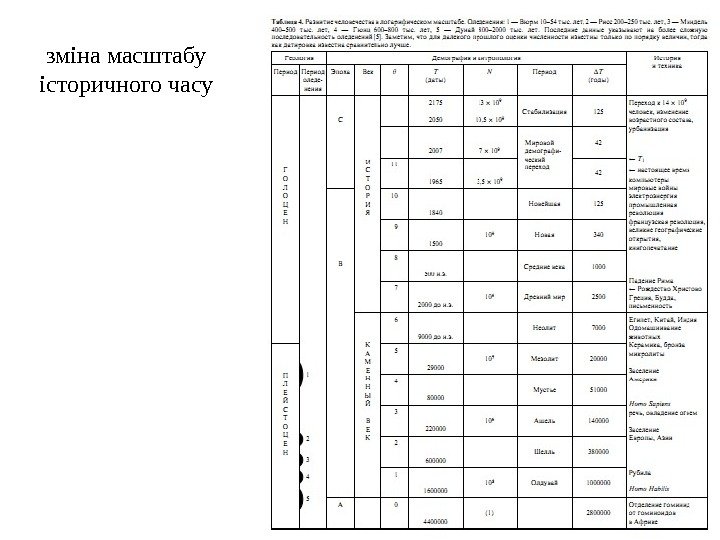
зміна масштабу історичного часу

Історична хронологія і астрономія

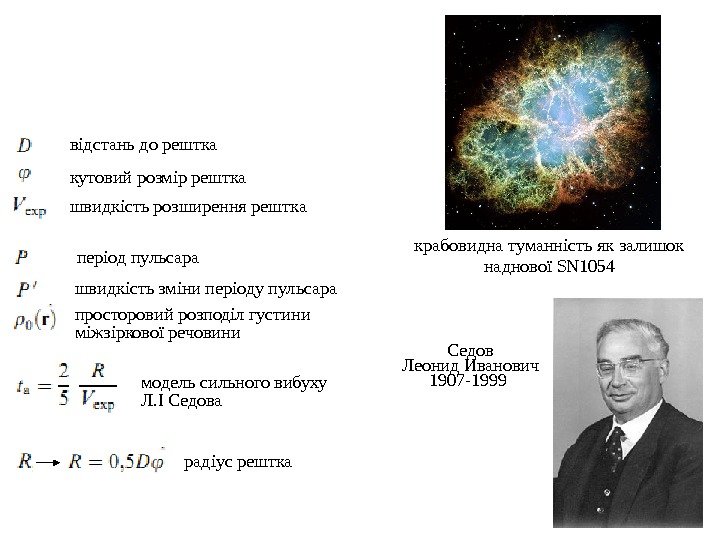
відстань до рештка кутовий розмір рештка швидкість розширення рештка період пульсара швидкість зміни періоду пульсара просторовий розподіл густини міжзіркової речовини модель сильного вибуху Л. І Седова радіус рештка крабовидна туманність як залишок наднової SN 1054 Седов Леонид Иванович 1907 —

п араметри історичних наднових сучасні значення періоду і швидкості зміни періоду радіопульсара початкове значення періоду