Презентация Занятие 1 in english





































- Размер: 205 Кб
- Количество слайдов: 40
Описание презентации Презентация Занятие 1 in english по слайдам
 1. Constants and variables Переменные и константы в MATLAB могут быть в основном : векторами-столбцами векторами-строками двухмерными матрицами многомерными матрицами Многие библиотечные векторные функции обычно ожидают в качестве входных параметров именно векторы-столбцы ! Далее рассмотрим, как создавать переменные / константы
1. Constants and variables Переменные и константы в MATLAB могут быть в основном : векторами-столбцами векторами-строками двухмерными матрицами многомерными матрицами Многие библиотечные векторные функции обычно ожидают в качестве входных параметров именно векторы-столбцы ! Далее рассмотрим, как создавать переменные / константы
 1. Constants and variables the creation of a column vector : a = [ 10 ; 20 ; 30 ]; a = the creating of a row vector: b = [ 10 20 30 ]; или b = [ 10 , 20 , 30 ]; the creation of two-dimensional matrix: c = [ 1 2 3 ; 4 5 6 ; 7 8 9 ]; или c = [ 1 2 3; … 4 5 6; … 7 8 9 ];
1. Constants and variables the creation of a column vector : a = [ 10 ; 20 ; 30 ]; a = the creating of a row vector: b = [ 10 20 30 ]; или b = [ 10 , 20 , 30 ]; the creation of two-dimensional matrix: c = [ 1 2 3 ; 4 5 6 ; 7 8 9 ]; или c = [ 1 2 3; … 4 5 6; … 7 8 9 ];
![1. Constants and variables empty matrix: e = [ ]; 1. Constants and variables empty matrix: e = [ ];](/docs//zanyatie_1_in_english_images/zanyatie_1_in_english_2.jpg) 1. Constants and variables empty matrix: e = [ ]; e = row vector ( : — colon ) s = [ 1 : 10 ]; или s = [ 1 : 10 ]; column vector ( : ) w = [ 1 : -0. 1 : 0. 5 ]; w = 1 2 3 4 5 6 7 8 9 10 1 0. 9 0. 8 0. 7 0. 6 0.
1. Constants and variables empty matrix: e = [ ]; e = row vector ( : — colon ) s = [ 1 : 10 ]; или s = [ 1 : 10 ]; column vector ( : ) w = [ 1 : -0. 1 : 0. 5 ]; w = 1 2 3 4 5 6 7 8 9 10 1 0. 9 0. 8 0. 7 0. 6 0.
 1. Constants and variables matrix from the matrices : a = [ 1 2 3 ]; a = b = [ 4 5 6 ]; b = c = [ a b ]; c = d = [ a ; b ]; d =
1. Constants and variables matrix from the matrices : a = [ 1 2 3 ]; a = b = [ 4 5 6 ]; b = c = [ a b ]; c = d = [ a ; b ]; d =
 1. Constants and variables using of ‘ operator (transponding) in matrices creation: a = [ 1 2 3 ]; a = b = a’; или b = [ 1 2 3 ]’; c = [ 1 2 ; 3 4 ; 5 6 ]; c = d = c’; d =
1. Constants and variables using of ‘ operator (transponding) in matrices creation: a = [ 1 2 3 ]; a = b = a’; или b = [ 1 2 3 ]’; c = [ 1 2 ; 3 4 ; 5 6 ]; c = d = c’; d =
 Task 1. Create following variables by using previous commands in command window: 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 a = -1. 5 -1. 0 -0. 5 0. 0 0. 5 1. 5 2. 0 x = 1 2 3 4 5 6 7 y =
Task 1. Create following variables by using previous commands in command window: 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1 a = -1. 5 -1. 0 -0. 5 0. 0 0. 5 1. 5 2. 0 x = 1 2 3 4 5 6 7 y =
 1. Constants and variables Using special functions to creation of matrices and vectors: 0 0 0 0 0 1 1 0 0 0 1 a = zeros( 2 , 5 ); a = b = ones( 3 , 1 ); b = c = eye( 3 ); c =
1. Constants and variables Using special functions to creation of matrices and vectors: 0 0 0 0 0 1 1 0 0 0 1 a = zeros( 2 , 5 ); a = b = ones( 3 , 1 ); b = c = eye( 3 ); c =
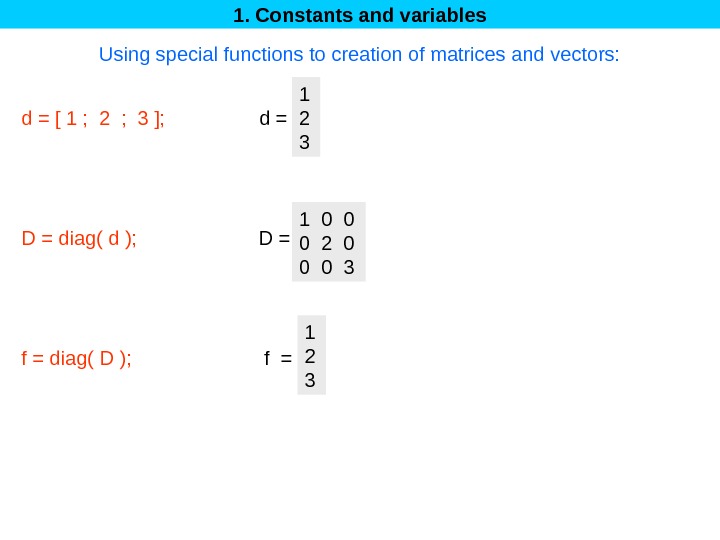
 1. Constants and variables Using special functions to creation of matrices and vectors: 1 2 3 1 0 0 0 2 0 0 0 3 d = [ 1 ; 2 ; 3 ]; d = D = diag( d ); D = f = diag( D ); f =
1. Constants and variables Using special functions to creation of matrices and vectors: 1 2 3 1 0 0 0 2 0 0 0 3 d = [ 1 ; 2 ; 3 ]; d = D = diag( d ); D = f = diag( D ); f =
 1. Constants and variables Using special functions to creation of matrices and vectors: 0. 76 0. 12 0. 91 0. 59 0. 37 0. 390. 99 0. 13 0. 75 0. 11 0. 64 0. 00 0. 46 0. 91 0. 32 -0. 43 -1. 66 0. 12 -0. 68 2. 14 Uniform distribution of random numbers {0. . 1} r 1 = rand( 2 , 3 ); r 1 = r 2 = rand( 3 ); r 2 = Normal distribution of random numbers {-inf. . +inf} r 3 = randn( 1 , 5 ); r 3 = r 4 = randn( 2 ); r 4 = 0. 56 -1. 26 0. 12 0. 18 Expected value = 0 Dispersion x =
1. Constants and variables Using special functions to creation of matrices and vectors: 0. 76 0. 12 0. 91 0. 59 0. 37 0. 390. 99 0. 13 0. 75 0. 11 0. 64 0. 00 0. 46 0. 91 0. 32 -0. 43 -1. 66 0. 12 -0. 68 2. 14 Uniform distribution of random numbers {0. . 1} r 1 = rand( 2 , 3 ); r 1 = r 2 = rand( 3 ); r 2 = Normal distribution of random numbers {-inf. . +inf} r 3 = randn( 1 , 5 ); r 3 = r 4 = randn( 2 ); r 4 = 0. 56 -1. 26 0. 12 0. 18 Expected value = 0 Dispersion x =
 1. Constants and variables Using special functions to creation of matrices and vectors: 1 2 1 2 Replication of matrix: a = [ 1 2 ]; a = b = repmat( a, 3 , 2 ); b =
1. Constants and variables Using special functions to creation of matrices and vectors: 1 2 1 2 Replication of matrix: a = [ 1 2 ]; a = b = repmat( a, 3 , 2 ); b =
 Task 1. Create following variables by using previous functions: 1 0 0 0 2 0 0 0 3 0 0 0 4 0 0 0 5 a = 1 2 3 4 1 2 3 4 c =
Task 1. Create following variables by using previous functions: 1 0 0 0 2 0 0 0 3 0 0 0 4 0 0 0 5 a = 1 2 3 4 1 2 3 4 c =
 1. Constants and variables Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = [ 1 2 3 4 ; … 5 6 7 8 ; … 2 2 ; … 3 4 5 3 ]; a = x = a( 2 , 3 ); y = a( 4 , 3 ); 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = x = 7 y =
1. Constants and variables Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = [ 1 2 3 4 ; … 5 6 7 8 ; … 2 2 ; … 3 4 5 3 ]; a = x = a( 2 , 3 ); y = a( 4 , 3 ); 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = x = 7 y =
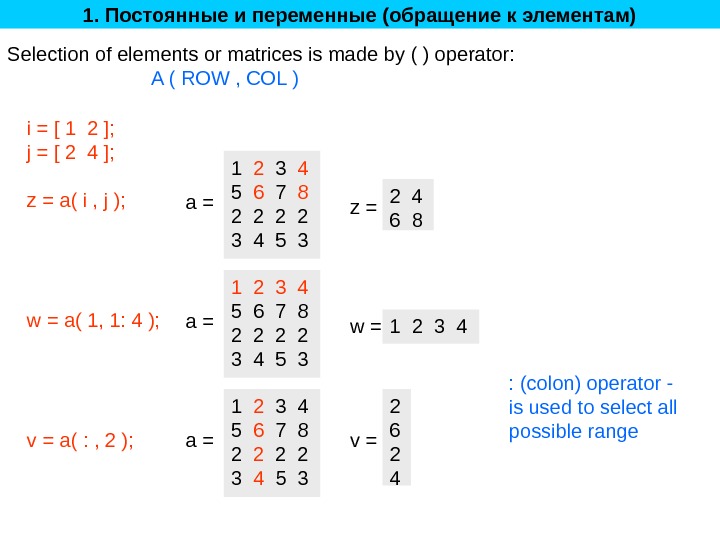
 1. Постоянные и переменные (обращение к элементам) Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a =i = [ 1 2 ]; j = [ 2 4 ]; z = a( i , j ); w = a( 1, 1: 4 ); v = a( : , 2 ); z = 2 4 6 8 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = w = 1 2 3 4 1 2 3 4 5 6 7 8 2 2 2 2 3 4 5 3 a = v = 2 6 2 4 : (colon) operator — is used to select all possible range
1. Постоянные и переменные (обращение к элементам) Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a =i = [ 1 2 ]; j = [ 2 4 ]; z = a( i , j ); w = a( 1, 1: 4 ); v = a( : , 2 ); z = 2 4 6 8 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = w = 1 2 3 4 1 2 3 4 5 6 7 8 2 2 2 2 3 4 5 3 a = v = 2 6 2 4 : (colon) operator — is used to select all possible range
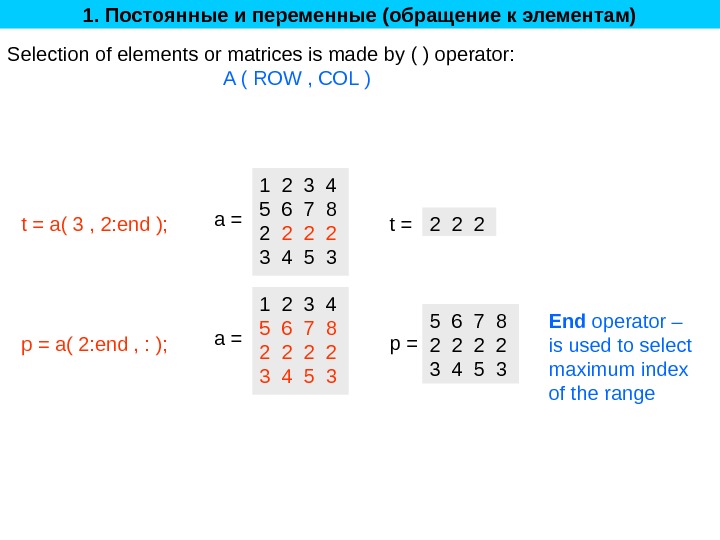
 1. Постоянные и переменные (обращение к элементам) Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) 1 2 3 4 5 6 7 8 2 2 2 2 3 4 5 3 a = t = a( 3 , 2: end ); p = a( 2: end , : ); t = 2 2 2 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = p = 5 6 7 8 2 2 3 4 5 3 End operator – is used to select maximum index of the range
1. Постоянные и переменные (обращение к элементам) Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) 1 2 3 4 5 6 7 8 2 2 2 2 3 4 5 3 a = t = a( 3 , 2: end ); p = a( 2: end , : ); t = 2 2 2 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = p = 5 6 7 8 2 2 3 4 5 3 End operator – is used to select maximum index of the range
 1. Постоянные и переменные (обращение к элементам) Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) After filling nonexistent elements of matrix, missing elements will be created and filled by zero value 1 2 3 4 a =a( 4 , 5 ) = 9 ; 1 2 0 0 0 3 4 0 0 0 0 0 9 a = before after
1. Постоянные и переменные (обращение к элементам) Selection of elements or matrices is made by ( ) operator: A ( ROW , COL ) After filling nonexistent elements of matrix, missing elements will be created and filled by zero value 1 2 3 4 a =a( 4 , 5 ) = 9 ; 1 2 0 0 0 3 4 0 0 0 0 0 9 a = before after
 1. Постоянные и переменные (обращение к элементам) Обращение к отдельным элементам или частям матриц производится с помощью оператора ( ) : A ( ROW , COL ) Если оператор ( ) указывает на область и области присваивается скалярное значение, данное скалярное значение заполнит всю область : a =a( 1: 2 , 1: 2 ) = 0; a = до после
1. Постоянные и переменные (обращение к элементам) Обращение к отдельным элементам или частям матриц производится с помощью оператора ( ) : A ( ROW , COL ) Если оператор ( ) указывает на область и области присваивается скалярное значение, данное скалярное значение заполнит всю область : a =a( 1: 2 , 1: 2 ) = 0; a = до после
 1. Постоянные и переменные (обращение к элементам) Обращение к отдельным элементам или частям матриц производится с помощью оператора ( ) : A ( ROW , COL ) Можно “ вставлять ” значения одной матрицы внутрь другой : a( 1: 2 , 2: 3 ) = b; a = до после 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = 7 7 5 5 b =
1. Постоянные и переменные (обращение к элементам) Обращение к отдельным элементам или частям матриц производится с помощью оператора ( ) : A ( ROW , COL ) Можно “ вставлять ” значения одной матрицы внутрь другой : a( 1: 2 , 2: 3 ) = b; a = до после 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = 7 7 5 5 b =
 1. Постоянные и переменные (обращение к элементам) Обращение к отдельным элементам или частям матриц производится с помощью оператора ( ) : A ( ROW , COL ) Для удаления частей матрицы используется пустая матрица : [ ] a( 2 , : ) = [ ]; a = до после 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = 1 2 3 4 2 2 3 4 5 31 2 3 4 5 6 7 8 2 2 3 4 5 3 a =
1. Постоянные и переменные (обращение к элементам) Обращение к отдельным элементам или частям матриц производится с помощью оператора ( ) : A ( ROW , COL ) Для удаления частей матрицы используется пустая матрица : [ ] a( 2 , : ) = [ ]; a = до после 1 2 3 4 5 6 7 8 2 2 3 4 5 3 a = 1 2 3 4 2 2 3 4 5 31 2 3 4 5 6 7 8 2 2 3 4 5 3 a =
 ЗАДАНИЕ 1. Создайте следующие переменные, вводя необходимые команды в командном окне : 1 2 0 0 0 3 4 0 0 0 0 0 0 1 2 3 a = 2. С помощью единственной команды удалите 2, 3, 7 столбцы матрицы a 3. Создайте матрицу b, содержащую 2 и 3 строки “ урезанной ” матрицы а 4. Удалите переменную а
ЗАДАНИЕ 1. Создайте следующие переменные, вводя необходимые команды в командном окне : 1 2 0 0 0 3 4 0 0 0 0 0 0 1 2 3 a = 2. С помощью единственной команды удалите 2, 3, 7 столбцы матрицы a 3. Создайте матрицу b, содержащую 2 и 3 строки “ урезанной ” матрицы а 4. Удалите переменную а
 1. Постоянные и переменные (удаление) Для удаления переменных используют функцию clear : >> clear x y z; % удалили переменные x, y, z >> clear(‘a’, ’b’); % удалили переменные a, b >> clear all; % удалили все переменные >> clear(‘all’); % удалили все переменные >> clear global; % удалили все глобальные переменные >> clear(‘global’); % удалили все глобальные переменные
1. Постоянные и переменные (удаление) Для удаления переменных используют функцию clear : >> clear x y z; % удалили переменные x, y, z >> clear(‘a’, ’b’); % удалили переменные a, b >> clear all; % удалили все переменные >> clear(‘all’); % удалили все переменные >> clear global; % удалили все глобальные переменные >> clear(‘global’); % удалили все глобальные переменные
 1. Постоянные и переменные (строки) Строки ( char ) в MATLAB представляют собой массивы символов : str = ‘ это массив строк ’; b = str(1 : 3); % b = ‘ это ’ c = str( 5 : 10 ); % c = ‘ массив ’ d = [ b c ]; % d = ‘ этомассив ’
1. Постоянные и переменные (строки) Строки ( char ) в MATLAB представляют собой массивы символов : str = ‘ это массив строк ’; b = str(1 : 3); % b = ‘ это ’ c = str( 5 : 10 ); % c = ‘ массив ’ d = [ b c ]; % d = ‘ этомассив ’
 1. Постоянные и переменные (структуры) Структуры (structure) в MATLAB представляют собой объединения разнородных элементов : a. name = ‘ вася ’; a. m = 100; a. matr = [10; 20; 30]; или : a = struct( ‘name’ , ’ вася ’ , ‘m’ , 100 , ‘matr’, [ 10 ; 20 ; 30 ] ); name: ‘ вася ’ m: 100 matr: 1 0 20 30 a =
1. Постоянные и переменные (структуры) Структуры (structure) в MATLAB представляют собой объединения разнородных элементов : a. name = ‘ вася ’; a. m = 100; a. matr = [10; 20; 30]; или : a = struct( ‘name’ , ’ вася ’ , ‘m’ , 100 , ‘matr’, [ 10 ; 20 ; 30 ] ); name: ‘ вася ’ m: 100 matr: 1 0 20 30 a =
 1. Постоянные и переменные (ячейки) Ячейки (cell) в MATLAB представляют собой массивы любых, даже разнородных элементов : a { 1 , 1 } = ‘ петя ’; a { 1 , 2 } = pi; a { 2 , 1 } = [ 1 2 3 ; 4 5 6 ]; a { 2 , 2 } = int 8(10); ‘ петя ’ pi 1 2 3 10 4 5 6 a =
1. Постоянные и переменные (ячейки) Ячейки (cell) в MATLAB представляют собой массивы любых, даже разнородных элементов : a { 1 , 1 } = ‘ петя ’; a { 1 , 2 } = pi; a { 2 , 1 } = [ 1 2 3 ; 4 5 6 ]; a { 2 , 2 } = int 8(10); ‘ петя ’ pi 1 2 3 10 4 5 6 a =
 1. Постоянные и переменные (глобальные) В MATLAB присутствуют также глобальные переменные. Особенность этих переменных в том, что они могут быть видны вне функций. % главный скрипт global G; G = 10; % % функция myfunc [y] = myfunc(x); global G; % внутри функции MATLAB теперь “ знает ” , что y=G*x; % G — глобальная переменная, и нужно искать её % “ снаружи ”
1. Постоянные и переменные (глобальные) В MATLAB присутствуют также глобальные переменные. Особенность этих переменных в том, что они могут быть видны вне функций. % главный скрипт global G; G = 10; % % функция myfunc [y] = myfunc(x); global G; % внутри функции MATLAB теперь “ знает ” , что y=G*x; % G — глобальная переменная, и нужно искать её % “ снаружи ”
 1. Постоянные и переменные (комплексные числа) В MATLAB имеются также комплексные числа (переменные) : x = 2 + 3*j x = 2 + 3 j y = 7 – 4*i y = 7 – 4 i z = 5*i z = 5 i Для комплексных чисел также определены соответствующие математические операции и функции.
1. Постоянные и переменные (комплексные числа) В MATLAB имеются также комплексные числа (переменные) : x = 2 + 3*j x = 2 + 3 j y = 7 – 4*i y = 7 – 4 i z = 5*i z = 5 i Для комплексных чисел также определены соответствующие математические операции и функции.
 ЗАДАНИЕ 1. Создайте переменные следующих типов (с любыми значениями) : d – тип double ui — тип uint 16 s – структура с 2 мя — 3 мя полями c — тип массив ячеек ( cell) размером 2 на 3 z – комплексное число 2. Определите, к какому типу относится константа pi 3. Определите, к какому типу относится результат выражения 1<
ЗАДАНИЕ 1. Создайте переменные следующих типов (с любыми значениями) : d – тип double ui — тип uint 16 s – структура с 2 мя — 3 мя полями c — тип массив ячеек ( cell) размером 2 на 3 z – комплексное число 2. Определите, к какому типу относится константа pi 3. Определите, к какому типу относится результат выражения 1<
 Язык программирования MATLAB 2. Операторы и операции
Язык программирования MATLAB 2. Операторы и операции
 2. Операторы и операции (арифметические и матричные) Операторы : + сложение матриц одинаковых размеров A = [ 1 2 ; 3 4 ]; B = [ 2 2 ; 4 4 ]; C = A + B; — смена знака всех элементов матрицы на противоположный. A = [ 1 2 ; 3 4 ]; B = — A; — вычитание матриц одинаковых размеров A = [ 1 2 ; 3 4 ]; B = [ 2 2 ; 4 4 ]; C = A — B;
2. Операторы и операции (арифметические и матричные) Операторы : + сложение матриц одинаковых размеров A = [ 1 2 ; 3 4 ]; B = [ 2 2 ; 4 4 ]; C = A + B; — смена знака всех элементов матрицы на противоположный. A = [ 1 2 ; 3 4 ]; B = — A; — вычитание матриц одинаковых размеров A = [ 1 2 ; 3 4 ]; B = [ 2 2 ; 4 4 ]; C = A — B;
 2. Операторы и операции (арифметические и матричные) Операторы : * матричное умножение ( по правилам матричного умножения ) матриц соответствующих размеров A = [ 1 2 ; 3 4 ]; B = [ 2 2 2 ; 4 4 4 ]; C = A * B; 2 x 2 2 x 3 2 x 2 * 2 x 3 >> 2 x
2. Операторы и операции (арифметические и матричные) Операторы : * матричное умножение ( по правилам матричного умножения ) матриц соответствующих размеров A = [ 1 2 ; 3 4 ]; B = [ 2 2 2 ; 4 4 4 ]; C = A * B; 2 x 2 2 x 3 2 x 2 * 2 x 3 >> 2 x
 2. Операторы и операции (арифметические и матричные) Операторы : / матричное деление z = x / y; % число = число / число A = B / s; % матрица = матрица / число (поэлементно) A / B равносильно A * inv(B) ( только для квадратных матриц! ) Здесь inv(B) – функция нахождения обратной матрицы / применяется для решения матричных уравнений \ левое матричное деление A \ B равносильно inv(A) * B ( только для квадратных матриц! ) \ применяется для решения матричных уравнений
2. Операторы и операции (арифметические и матричные) Операторы : / матричное деление z = x / y; % число = число / число A = B / s; % матрица = матрица / число (поэлементно) A / B равносильно A * inv(B) ( только для квадратных матриц! ) Здесь inv(B) – функция нахождения обратной матрицы / применяется для решения матричных уравнений \ левое матричное деление A \ B равносильно inv(A) * B ( только для квадратных матриц! ) \ применяется для решения матричных уравнений
 2. Операторы и операции (арифметические и матричные) Операторы : . * поэлементное умножение массивов одинаковых размеров. C = A. * B равносильно C( i , j ) = A( i , j ) * B( i , j ). / поэлементное деление массивов одинаковых размеров. C = A. / B равносильно C( i , j ) = A( i , j ) / B( i , j ). \ поэлементное левое деление массивов одинаковых размеров. C = A. \ B равносильно C( i , j ) = B( i , j ) / A( i , j )
2. Операторы и операции (арифметические и матричные) Операторы : . * поэлементное умножение массивов одинаковых размеров. C = A. * B равносильно C( i , j ) = A( i , j ) * B( i , j ). / поэлементное деление массивов одинаковых размеров. C = A. / B равносильно C( i , j ) = A( i , j ) / B( i , j ). \ поэлементное левое деление массивов одинаковых размеров. C = A. \ B равносильно C( i , j ) = B( i , j ) / A( i , j )
 2. Операторы и операции (арифметические и матричные) Операторы : ^ возведение скаляра в степень : x = y ^ 2. 5 вычисление степени квадратной матрицы : B = A ^ 3 равносильно B = A * A. ^ поэлементное возведение матрицы в степени , являющиеся элементами другой матрицы тех же размеров : C = A. ^ B равносильно С( i , j ) = A( i , j ) ^ B( i , j )
2. Операторы и операции (арифметические и матричные) Операторы : ^ возведение скаляра в степень : x = y ^ 2. 5 вычисление степени квадратной матрицы : B = A ^ 3 равносильно B = A * A. ^ поэлементное возведение матрицы в степени , являющиеся элементами другой матрицы тех же размеров : C = A. ^ B равносильно С( i , j ) = A( i , j ) ^ B( i , j )
 2. Операторы и операции (арифметические и матричные) Операторы : ‘ Нахождение сопряжённой матрицы B = A’. ’ Нахождение транспонированной матрицы B = A. ’ ВНИМАНИЕ : для вещественных матриц операция поиска сопряжённой матрицы совпадает с операцией транспонирования. Поэтому часто используют A‘ а не A. ’
2. Операторы и операции (арифметические и матричные) Операторы : ‘ Нахождение сопряжённой матрицы B = A’. ’ Нахождение транспонированной матрицы B = A. ’ ВНИМАНИЕ : для вещественных матриц операция поиска сопряжённой матрицы совпадает с операцией транспонирования. Поэтому часто используют A‘ а не A. ’
 2. Операторы и операции (размеры векторов) Для определения размеров векторов используют функцию length: >> a = [ 1 2 3 4 5 ]; % вектор-строка >> length(a) ans= 5 >> b = [ 1 ; 2 ; 3 ; 4 ; 5 ]; % вектор-столбец >> length(a) ans=
2. Операторы и операции (размеры векторов) Для определения размеров векторов используют функцию length: >> a = [ 1 2 3 4 5 ]; % вектор-строка >> length(a) ans= 5 >> b = [ 1 ; 2 ; 3 ; 4 ; 5 ]; % вектор-столбец >> length(a) ans=
 2. Операторы и операции (размеры матриц) Для определения размеров векторов и матриц используют функцию size: >> A = [ 1 2 3 ; 4 5 6 ]; % матрица 2 x 3 >> size( A ) % вектор, содержащий столько элементов ans= % сколько размерностей у переменной 2 3 % rows cols >> size( A , 1 ) % число строк ( rows ) ans= 2 >> size( A , 2 ) % число столбцов ( cols) ans=
2. Операторы и операции (размеры матриц) Для определения размеров векторов и матриц используют функцию size: >> A = [ 1 2 3 ; 4 5 6 ]; % матрица 2 x 3 >> size( A ) % вектор, содержащий столько элементов ans= % сколько размерностей у переменной 2 3 % rows cols >> size( A , 1 ) % число строк ( rows ) ans= 2 >> size( A , 2 ) % число столбцов ( cols) ans=
 2. Операторы и операции (логические) Операции отношения x > y больше x >= y больше равно x < y меньше x <= y меньше равно x == y равно x ~= y не равно Логические операторы и функции (здесь a и b – логические выражения или переменные) a & b and(a, b) И a && b быстрое И a | b or(a, b) ИЛИ a | | b быстрое ИЛИ xor(a, b) ИСКЛЮЧАЮЩЕЕ ИЛИ ~a not(a) ОТРИЦАНИЕ
2. Операторы и операции (логические) Операции отношения x > y больше x >= y больше равно x < y меньше x <= y меньше равно x == y равно x ~= y не равно Логические операторы и функции (здесь a и b – логические выражения или переменные) a & b and(a, b) И a && b быстрое И a | b or(a, b) ИЛИ a | | b быстрое ИЛИ xor(a, b) ИСКЛЮЧАЮЩЕЕ ИЛИ ~a not(a) ОТРИЦАНИЕ
 2. Операторы и операции (побитовые) Побитовые операции определены только для неотрицательных целых чисел ( uint 32, uint 16, uint 8 ) с = bitand(a, b) с = bitor(a, b) с = bitxor(a, b) с = bitshift(a, shift, ressize) c = bitset(a, bit, 1) c = bitset(a, bit, 0) c = bitget(a, bit)
2. Операторы и операции (побитовые) Побитовые операции определены только для неотрицательных целых чисел ( uint 32, uint 16, uint 8 ) с = bitand(a, b) с = bitor(a, b) с = bitxor(a, b) с = bitshift(a, shift, ressize) c = bitset(a, bit, 1) c = bitset(a, bit, 0) c = bitget(a, bit)
 2. Операторы и операции (приоритеты) Приоритеты математических и логических операторов (в порядке убывания приоритета) : 1. выражения в скобках ( ) 2. функции пользователя, библиотек 3. функции and, or, not, xor 4. отрицание ~ 5. транспонирование, возведение в степень (в т. ч. поэлементное), унарные + и – 6. умножение и деление (в т. ч. поэлементное), 7. сложение и вычитание 8. операции отношения >, >=, <, <=, ==, ~= 9. &, |, &&, || ( в ранних версиях имели одинаковый приоритет! ) ПРИМЕЧАНИЕ : Если сомневаетесь – используйте скобки ( ) – точно не ошибётесь!
2. Операторы и операции (приоритеты) Приоритеты математических и логических операторов (в порядке убывания приоритета) : 1. выражения в скобках ( ) 2. функции пользователя, библиотек 3. функции and, or, not, xor 4. отрицание ~ 5. транспонирование, возведение в степень (в т. ч. поэлементное), унарные + и – 6. умножение и деление (в т. ч. поэлементное), 7. сложение и вычитание 8. операции отношения >, >=, <, <=, ==, ~= 9. &, |, &&, || ( в ранних версиях имели одинаковый приоритет! ) ПРИМЕЧАНИЕ : Если сомневаетесь – используйте скобки ( ) – точно не ошибётесь!
 ЗАДАНИЕ 1. Создайте следующие матрицы : 1 1 2 3 4 5 A = 4 3 B = 2. С помощью оператора \ найдите решение уравнения : A*X =
ЗАДАНИЕ 1. Создайте следующие матрицы : 1 1 2 3 4 5 A = 4 3 B = 2. С помощью оператора \ найдите решение уравнения : A*X =
 ЗАДАНИЕ ( продолжение) 2. С помощью оператора \ найдите решение уравнения : A*X = B ПОДСКАЗКА : A*X = B — делим слева на A A \ A*X = A \ B — то, что требовалось ДЛЯ ПРОВЕРКИ : A*X — должно получиться
ЗАДАНИЕ ( продолжение) 2. С помощью оператора \ найдите решение уравнения : A*X = B ПОДСКАЗКА : A*X = B — делим слева на A A \ A*X = A \ B — то, что требовалось ДЛЯ ПРОВЕРКИ : A*X — должно получиться
