Презентация Вопрос No.7 Статистические методы в QSAR — 2














vopros_no.7_statisticheskie_metody_v_qsar_-_2.ppt
- Размер: 2.8 Mегабайта
- Количество слайдов: 30
Описание презентации Презентация Вопрос No.7 Статистические методы в QSAR — 2 по слайдам
 Статистические методы в QSAR Часть 2 Многомерный анализ данных
Статистические методы в QSAR Часть 2 Многомерный анализ данных
 Затронутые темы • Многомерный анализ данных • Понятие о дескрипторном пространстве, химическом расстоянии • Понятие о дискриминантном и кластерном анализах • Метрика дескрипторного пространства. Коллинеарные и ортогональные дескрипторы • Латентные дескрипторы, оценки ( scores ) и нагрузки ( loading ) • Понятие о факторном анализе и методе главных компонент ( PCA ) • Метод частичных наименьших квадратов ( PLS)
Затронутые темы • Многомерный анализ данных • Понятие о дескрипторном пространстве, химическом расстоянии • Понятие о дискриминантном и кластерном анализах • Метрика дескрипторного пространства. Коллинеарные и ортогональные дескрипторы • Латентные дескрипторы, оценки ( scores ) и нагрузки ( loading ) • Понятие о факторном анализе и методе главных компонент ( PCA ) • Метод частичных наименьших квадратов ( PLS)
 Многомерный анализ данных N M NN M M xxx xxx X 21 22 2 2 1 11 2 1 1 N P NN P P yyy yyy Y 21 22 2 2 1 11 2 1 1 Традиционные регрессионные процедуры — число столбцов в матрицах дескрипторов X относительно невелико, и между ними отсутствуют линейные зависимости Процедуры многомерного анализа данных могут работать с матрицами дескрипторов X , содержащими большое количество столбцов, многие из которых линейно-зависимы
Многомерный анализ данных N M NN M M xxx xxx X 21 22 2 2 1 11 2 1 1 N P NN P P yyy yyy Y 21 22 2 2 1 11 2 1 1 Традиционные регрессионные процедуры — число столбцов в матрицах дескрипторов X относительно невелико, и между ними отсутствуют линейные зависимости Процедуры многомерного анализа данных могут работать с матрицами дескрипторов X , содержащими большое количество столбцов, многие из которых линейно-зависимы
 Центрирование данных для многомерного анализаj ix. X , гдеi j ixxx N k k iix N x 1 1 Mi, 1 j i y. Y , гдеi j i yyy N k k iiy N y 1 1 Pi,
Центрирование данных для многомерного анализаj ix. X , гдеi j ixxx N k k iix N x 1 1 Mi, 1 j i y. Y , гдеi j i yyy N k k iiy N y 1 1 Pi,
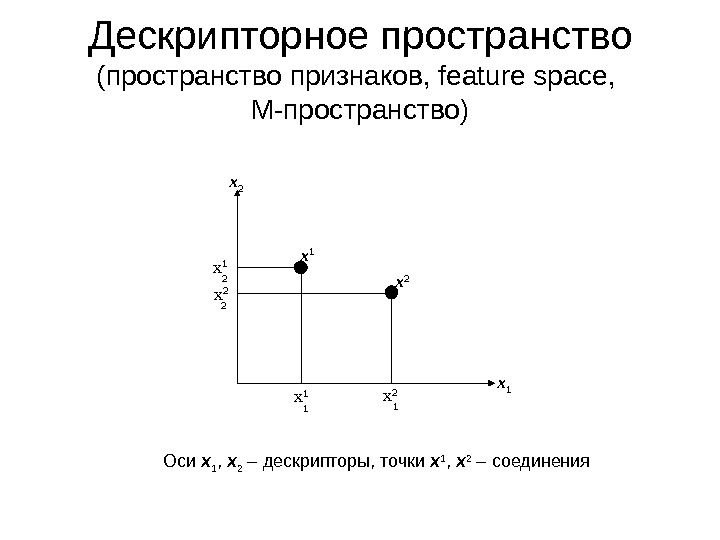
 x 1 x 2 x 1 x 2 x 2 x 1 1 12 2 Дескрипторное пространство (пространство признаков , feature space, M- пространство) Оси x 1 , x 2 – дескрипторы, точки x 1 , x 2 – соединения
x 1 x 2 x 1 x 2 x 2 x 1 1 12 2 Дескрипторное пространство (пространство признаков , feature space, M- пространство) Оси x 1 , x 2 – дескрипторы, точки x 1 , x 2 – соединения
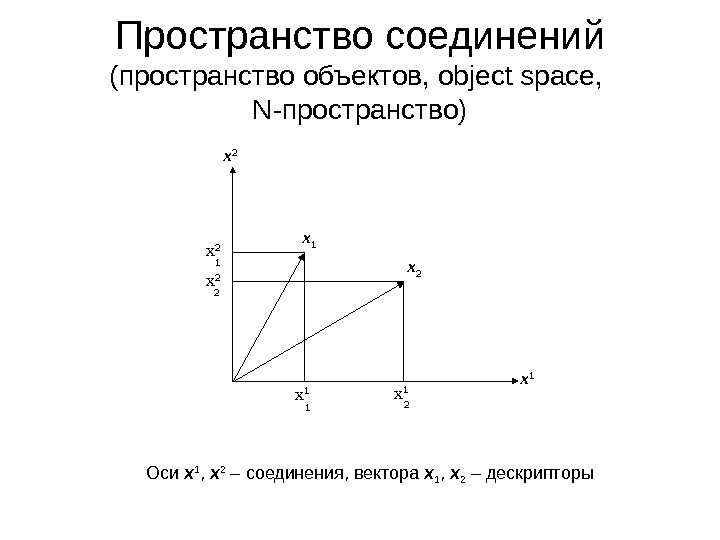
 x 2 x 1 x 1 x 2 x 2 2 12 1 Пространство соединений (пространство объектов, object space, N- пространство) Оси x 1 , x 2 – соединения, вектора x 1 , x 2 – дескрипторы
x 2 x 1 x 1 x 2 x 2 2 12 1 Пространство соединений (пространство объектов, object space, N- пространство) Оси x 1 , x 2 – соединения, вектора x 1 , x 2 – дескрипторы
 Метрика дескрипторного пространства (химическое расстояние) Эвклидово расстояние Манхэттоновское расстояние Метрика Минковского M k j k i k Euclid ijxx. D 1 2)( M k j k i k Manhat ijxx. D 1 tan r M k rj k i k Minkowski ijxx.
Метрика дескрипторного пространства (химическое расстояние) Эвклидово расстояние Манхэттоновское расстояние Метрика Минковского M k j k i k Euclid ijxx. D 1 2)( M k j k i k Manhat ijxx. D 1 tan r M k rj k i k Minkowski ijxx.
 Принцип сходства ( Similarity Principle ) Постулируется принцип : структурно близкие химические соединения обладают сходными свойствами Предполагается, что всегда можно найти такой набор дескрипторов и такую метрику дескрипторного пространства, чтобы этот принцип выполнялся
Принцип сходства ( Similarity Principle ) Постулируется принцип : структурно близкие химические соединения обладают сходными свойствами Предполагается, что всегда можно найти такой набор дескрипторов и такую метрику дескрипторного пространства, чтобы этот принцип выполнялся
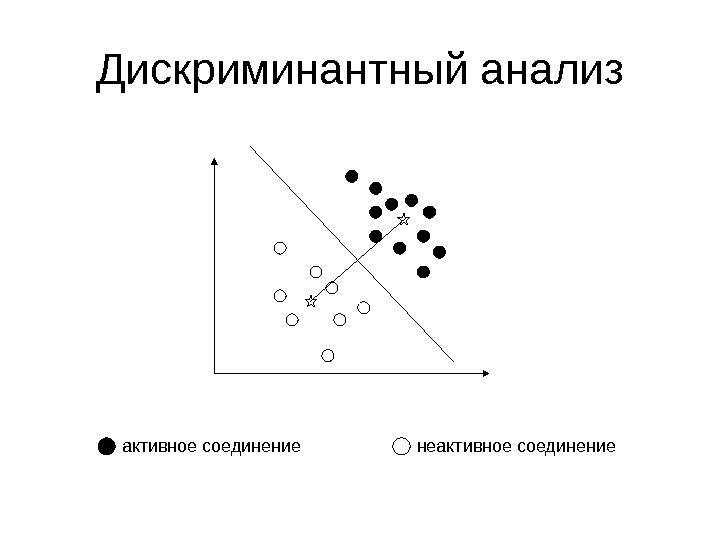
 Дискриминантный анализ активное соединение неактивное соединение
Дискриминантный анализ активное соединение неактивное соединение
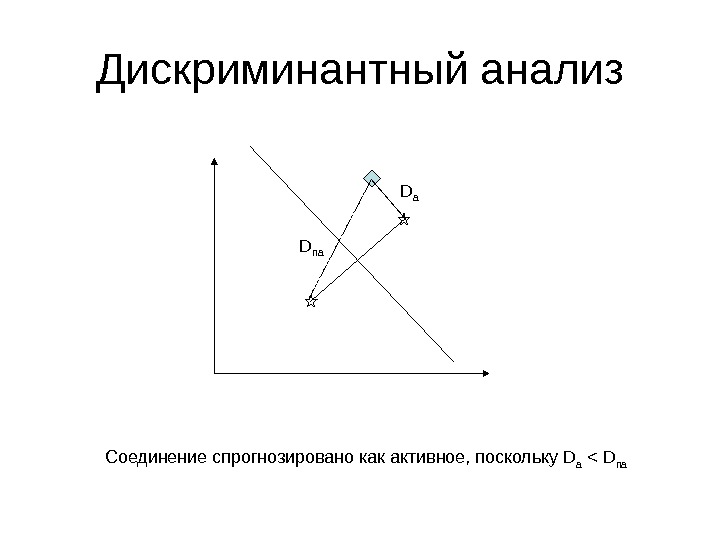
 Дискриминантный анализ D a D na Соединение спрогнозировано как активное, поскольку D a < D na
Дискриминантный анализ D a D na Соединение спрогнозировано как активное, поскольку D a < D na
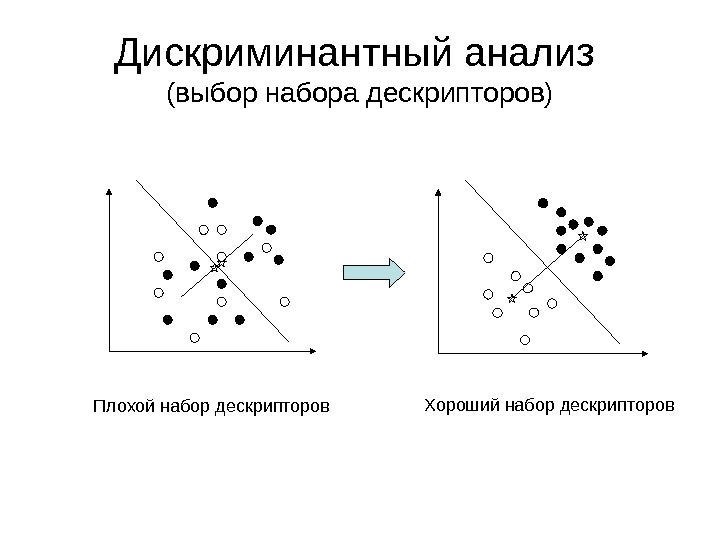
 Дискриминантный анализ (выбор набора дескрипторов) Плохой набор дескрипторов Хороший набор дескрипторов
Дискриминантный анализ (выбор набора дескрипторов) Плохой набор дескрипторов Хороший набор дескрипторов
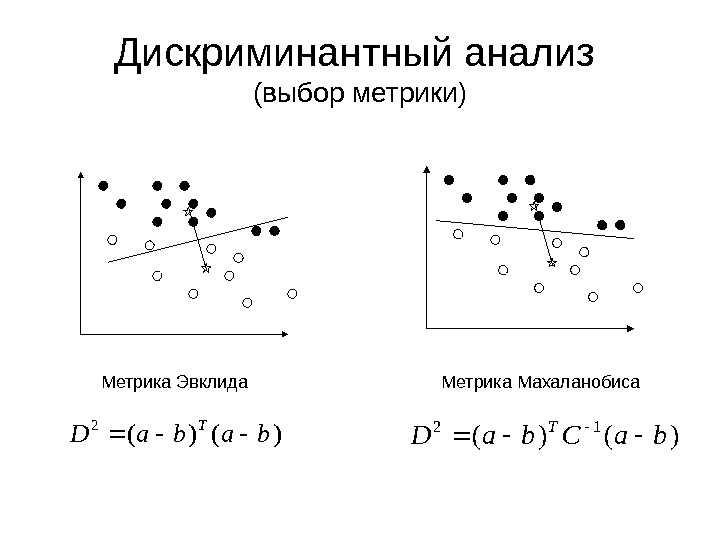
 Дискриминантный анализ (выбор метрики) Метрика Эвклида Метрика Махаланобиса)()( 2 baba. D T )()( 12 ba. Cba. D T
Дискриминантный анализ (выбор метрики) Метрика Эвклида Метрика Махаланобиса)()( 2 baba. D T )()( 12 ba. Cba. D T
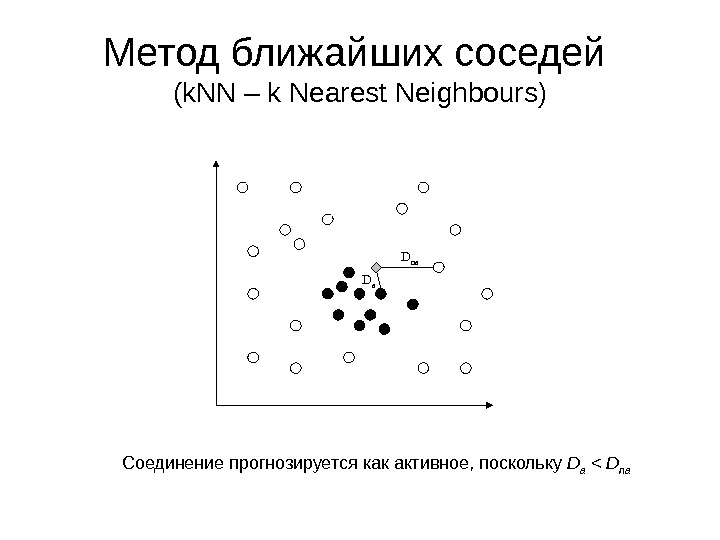
 Метод ближайших соседей ( k. NN – k Nearest Neighbours ) D a D na Соединение прогнозируется как активное, поскольку D a < D na
Метод ближайших соседей ( k. NN – k Nearest Neighbours ) D a D na Соединение прогнозируется как активное, поскольку D a < D na
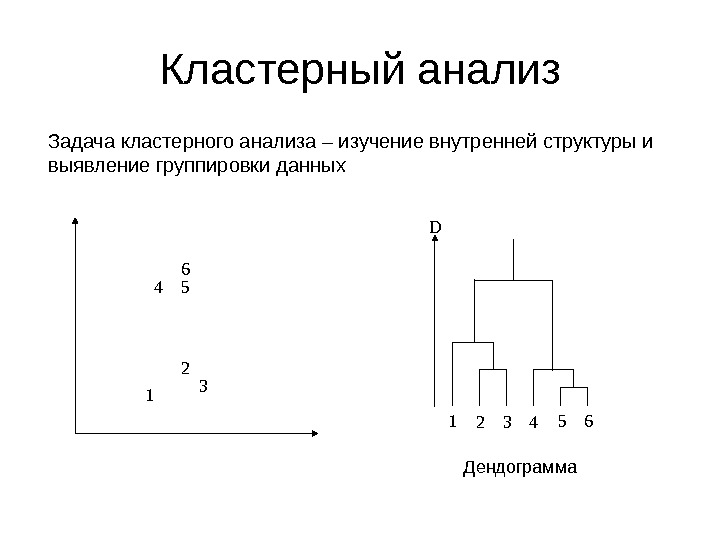
 Кластерный анализ Задача кластерного анализа – изучение внутренней структуры и выявление группировки данных 1 2 34 56 1 2 3 4 5 6 D Дендограмма
Кластерный анализ Задача кластерного анализа – изучение внутренней структуры и выявление группировки данных 1 2 34 56 1 2 3 4 5 6 D Дендограмма
 Свойства пространства соединений N k k j k ijixxxx 1 — скалярное произведение векторов N k k j. N k k i. N k k jk i xx xx 1 21 )()( cos — косинус угла между векторами N k k j k iijxx N с 11 1 — ковариация jjii ij ij cc c r — коэффициент корреляции
Свойства пространства соединений N k k j k ijixxxx 1 — скалярное произведение векторов N k k j. N k k i. N k k jk i xx xx 1 21 )()( cos — косинус угла между векторами N k k j k iijxx N с 11 1 — ковариация jjii ij ij cc c r — коэффициент корреляции
 Свойства пространства соединенийcos ij r Коллинеарные вектора – дескрипторы статистически эквивалентны Перпендикулярные вектора – дескрипторы линейно независимы
Свойства пространства соединенийcos ij r Коллинеарные вектора – дескрипторы статистически эквивалентны Перпендикулярные вектора – дескрипторы линейно независимы
 Латентные переменные Одной из главных задач многомерного анализа данных является выявление таких комбинаций исходных переменных (дескрипторов), которые бы позволили эффективно решать актуальные задачи: 1. Описать данные наименьшим числом переменных (факторный анализ) 2. Добиться максимального разделения классов (факторный дискриминантных анализ) 3. Построить регрессионную модель с наилучшей прогнозирующей способностью (метод частичный наименьших квадратов) 4. и т. д. Подобные комбинации исходных переменных называются латентными переменными (скрытыми факторами, оценками)
Латентные переменные Одной из главных задач многомерного анализа данных является выявление таких комбинаций исходных переменных (дескрипторов), которые бы позволили эффективно решать актуальные задачи: 1. Описать данные наименьшим числом переменных (факторный анализ) 2. Добиться максимального разделения классов (факторный дискриминантных анализ) 3. Построить регрессионную модель с наилучшей прогнозирующей способностью (метод частичный наименьших квадратов) 4. и т. д. Подобные комбинации исходных переменных называются латентными переменными (скрытыми факторами, оценками)
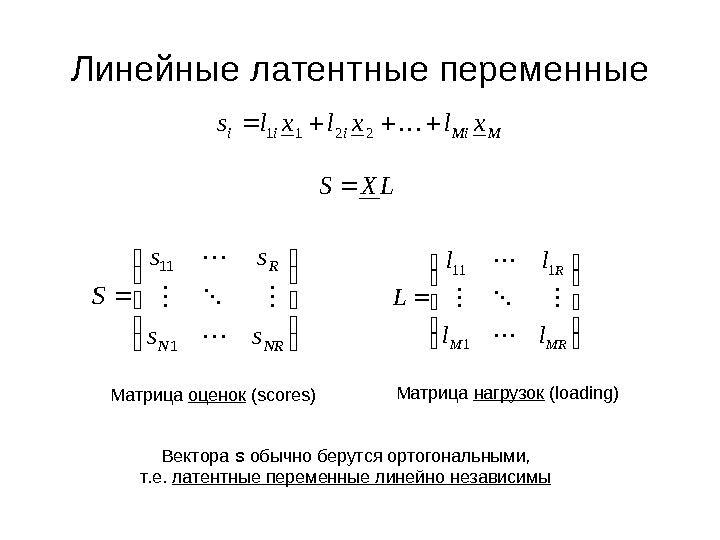
 Линейные латентные переменные M Miiii xlxlxls 2 21 1 LXS NRN R ss ss S 111 MRM R ll ll L 1 111 Матрица оценок ( scores ) Матрица нагрузок (loading) Вектора s обычно берутся ортогональными, т. е. латентные переменные линейно независимы
Линейные латентные переменные M Miiii xlxlxls 2 21 1 LXS NRN R ss ss S 111 MRM R ll ll L 1 111 Матрица оценок ( scores ) Матрица нагрузок (loading) Вектора s обычно берутся ортогональными, т. е. латентные переменные линейно независимы
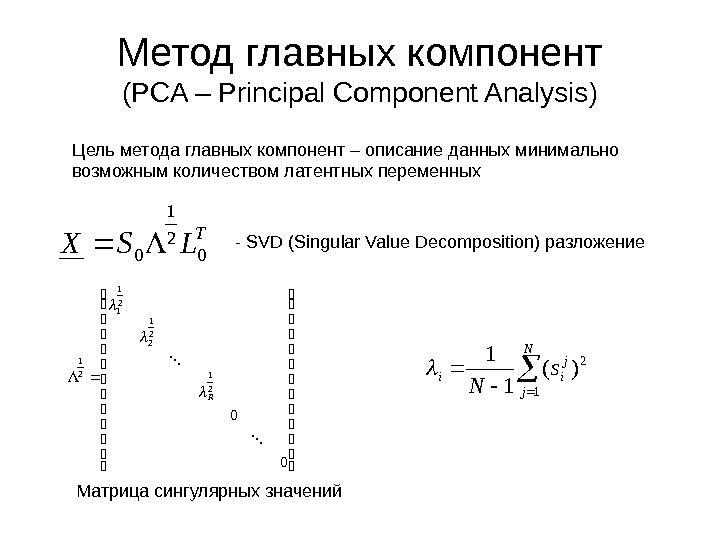
 Метод главных компонент ( PCA – Principal Component Analysis ) Цель метода главных компонент – описание данных минимально возможным количеством латентных переменных. T LSX 0 2 1 0 — SVD (Singular Value Decomposition) разложение 00 2 1 2 2 1 1 2 1 R Матрица сингулярных значений N j j iis N 1 2)(
Метод главных компонент ( PCA – Principal Component Analysis ) Цель метода главных компонент – описание данных минимально возможным количеством латентных переменных. T LSX 0 2 1 0 — SVD (Singular Value Decomposition) разложение 00 2 1 2 2 1 1 2 1 R Матрица сингулярных значений N j j iis N 1 2)(
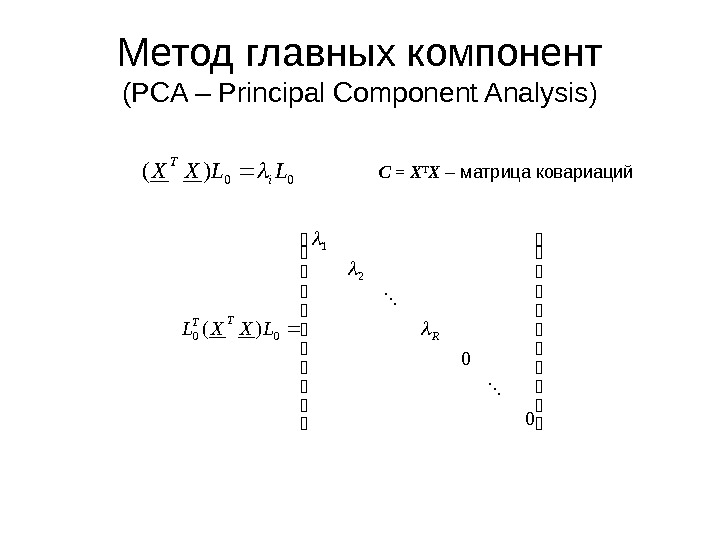
 Метод главных компонент ( PCA – Principal Component Analysis ) C = X T X – матрица ковариаций 00)(LLXXi T 00)( 2 1 00 R TT LXXL
Метод главных компонент ( PCA – Principal Component Analysis ) C = X T X – матрица ковариаций 00)(LLXXi T 00)( 2 1 00 R TT LXXL
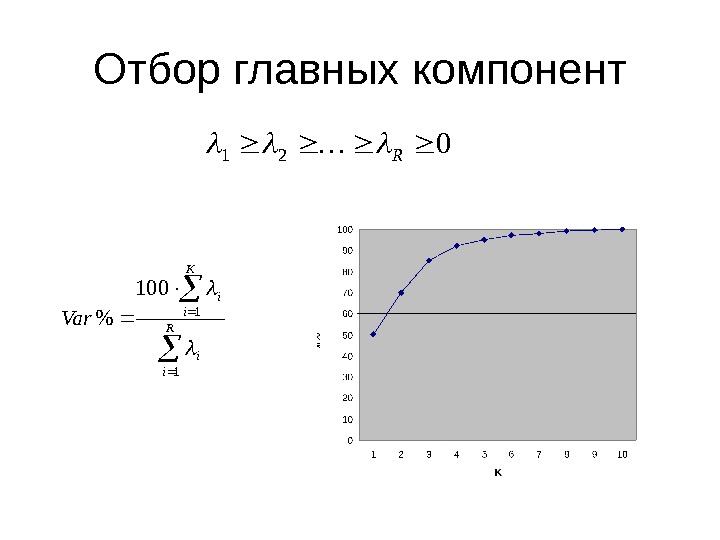
 Отбор главных компонент021 R R i i K i i Var 1 1 100 %
Отбор главных компонент021 R R i i K i i Var 1 1 100 %
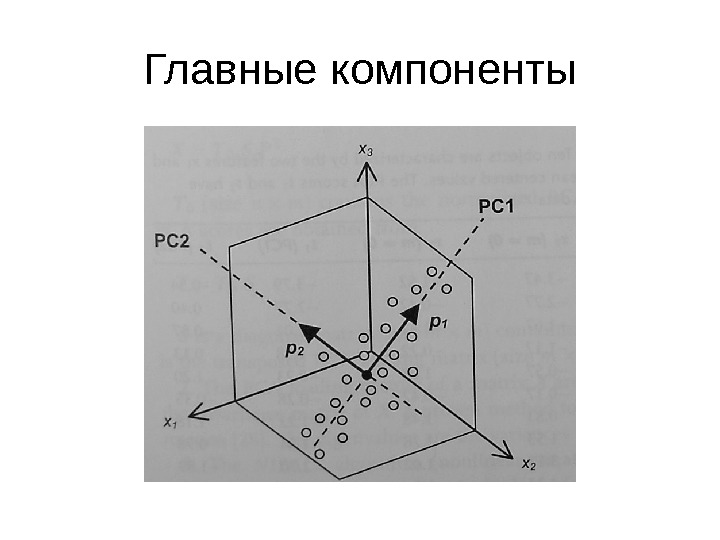
 Главные компоненты
Главные компоненты
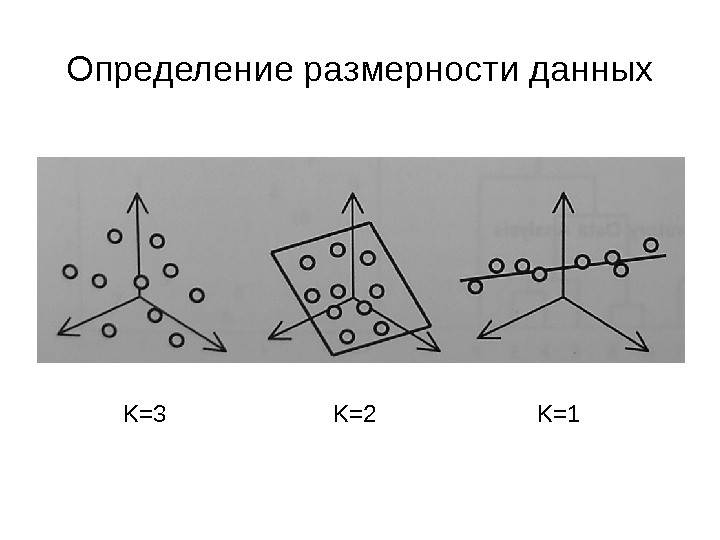
 Определение размерности данных K=3 K=2 K=
Определение размерности данных K=3 K=2 K=
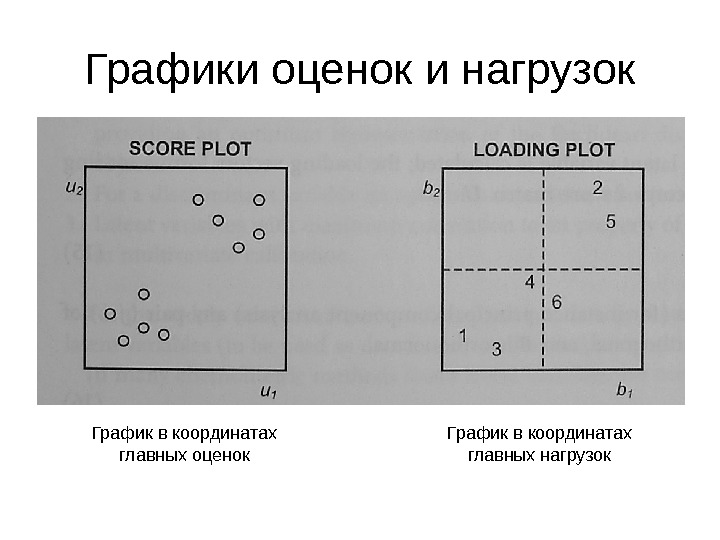
 Графики оценок и нагрузок График в координатах главных оценок График в координатах главных нагрузок
Графики оценок и нагрузок График в координатах главных оценок График в координатах главных нагрузок
 Резюме метода главных компонент • Вычисляется матрица ковариаций • Находятся ее собственные вектора и собственные значения • Отбираются латентные переменные, соответствующие двум наибольшим собственным значениям • Строятся 2 -мерные графики оценок и нагрузок
Резюме метода главных компонент • Вычисляется матрица ковариаций • Находятся ее собственные вектора и собственные значения • Отбираются латентные переменные, соответствующие двум наибольшим собственным значениям • Строятся 2 -мерные графики оценок и нагрузок
 Факторный анализ • Определяется число латентных переменных, необходимых для воспроизведения данных с заданной точностью • Путем вращения векторов исходных латентных переменных ищутся легко интерпретируемые варианты
Факторный анализ • Определяется число латентных переменных, необходимых для воспроизведения данных с заданной точностью • Путем вращения векторов исходных латентных переменных ищутся легко интерпретируемые варианты
 Факторный (канонический) дискриминантный анализ • Ищутся латентные переменные, позволяющие получить наилучшее разделение классов путем максимизации отношения межгрупповой к общей дисперсии
Факторный (канонический) дискриминантный анализ • Ищутся латентные переменные, позволяющие получить наилучшее разделение классов путем максимизации отношения межгрупповой к общей дисперсии
 Метод частичных наименьших квадратов ( PLS – Partial Least Squares ) В методе частичных наименьших квадратов ищется набор латентных переменных, позволяющий получить регрессионную модель с наилучшей прогнозирующей способностью K k j kk j say 1 M lk j iik j kxls MM xcxccy . . .
Метод частичных наименьших квадратов ( PLS – Partial Least Squares ) В методе частичных наименьших квадратов ищется набор латентных переменных, позволяющий получить регрессионную модель с наилучшей прогнозирующей способностью K k j kk j say 1 M lk j iik j kxls MM xcxccy . . .
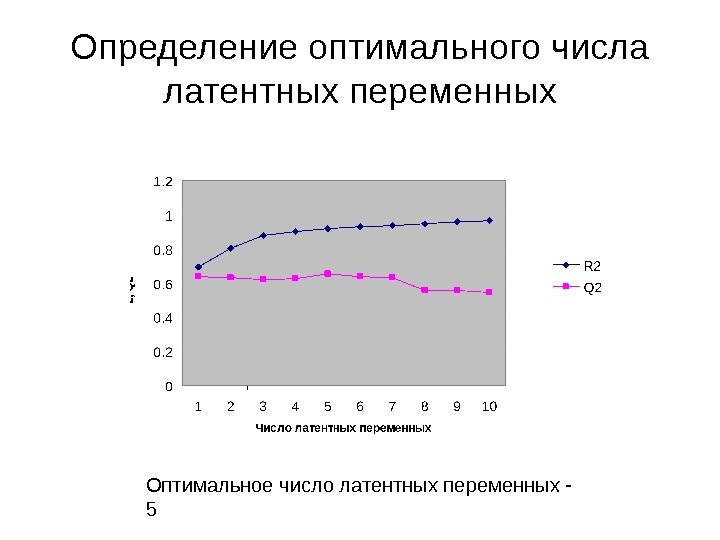
 Определение оптимального числа латентных переменных Оптимальное число латентных переменных —
Определение оптимального числа латентных переменных Оптимальное число латентных переменных —
 Резюме метода PLS • Один за одним отбираются латентные переменные, максимально коллинеарные с вектороми свойств или ошибок • При помощи процедуры скользящего контроля определяется прогнозирующая способность модели • Выбирается оптимальное число латентных переменных К , максимизирующее критерий Q 2 • Построенная на K латентных переменных регрессионная модель далее используется в для прогноза
Резюме метода PLS • Один за одним отбираются латентные переменные, максимально коллинеарные с вектороми свойств или ошибок • При помощи процедуры скользящего контроля определяется прогнозирующая способность модели • Выбирается оптимальное число латентных переменных К , максимизирующее критерий Q 2 • Построенная на K латентных переменных регрессионная модель далее используется в для прогноза
