Презентация Вопрос No.6 Статистические методы в QSAR — 1

Статистические методы в QSAR Часть 1 Множественная линейная регрессия

Затронутые темы • Задача статистического анализа в QSAR • Множественная линейная регрессия • Статистические показатели: R, s, F • Пошаговый вариант множественной линейной регрессии • Разбиение выборки на обучающую и контрольную • Процедура скользящего контроля

Задача статистического анализа в QSAR Целью статистического анализа в QSAR является поиск функции f , связывающей значение свойства y (которое может быть как физико-химическим свойством, так и биологической активностью) со значениями дескрипторов x 1, …, x. M , описывающих химическое соединение : ), . . . , ( 1 M xxfy Y непрерывное – регрессионный анализ, аппроксимация функции Y дискретное – дискриминантный анализ, классификация, распознавание образов

Задача статистического анализа в QSARjj M jj exxfy), . . . , (1 j =1, …, N jj M j P j exxcc. Fy), . . . , ; , . . . , (11 Принцип максимального правдоподобия max), . . . , (1 Pcc. L

Метод наименьших квадратов • Выборка является репрезентативной • Случайная величина ε имеет нормальное распределение • Наблюдения являются независимыми • Наблюдения являются равноточными N j j e 1 2 min)(

Множественная линейная регрессия – постановка задачи MMxcxccy. . . 110 M i jj ii j exccy 1 0 j = 1, …, N N j je 1 2 min)( Найти такие значения C i :

Множественная линейная регрессия – решение задачи. YXXXC TT 1 )( Mc c c C 1 0 N y y y Y 21 N M M xx xx xx X 1 22 1 11 1 1 Регрессионные коэффициенты Экспериментальные значения свойства Значения дескрипторов

Статистические показатели для МЛР N j j e. RSS 1 2 )( RSS – сумма квадратов остатков SS – дисперсия свойства Y N j jyy. SS 1 2)( N j j y N y 1 1 R – коэффициент корреляции SS RSSSS R O<R<1 Radj – скорректированный коэффициент корреляции 1 )1(22 MN M RRRadj

Статистические показатели для МЛР RMSE – среднеквадратичное значение ошибки. N RSS RMSE s – стандартное отклонение 1 MN RSS s MAE – средняя абсолютная ошибка N j j e N MAE 1 1 F – критерий Фишера )1/()( MNRSS MRSSSS

Статистические показатели для МЛР Показатели описательной способности линейной регрессионной модели Показатели прогнозирующей способности линейной регрессионной модели R R adj RMSE s M

Статистические показатели для МЛР

Статистические показатели для МЛР

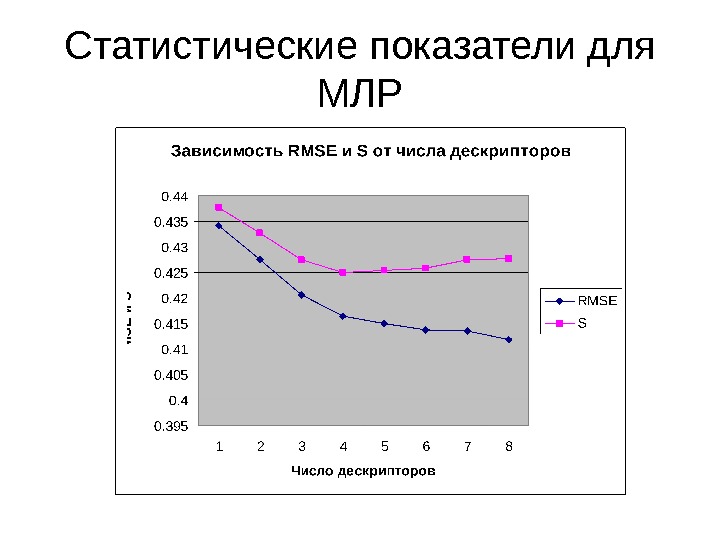
Статистические показатели для МЛР Индивидуальный t- критерий (критерий Стьюдента) для дескриптораii i i as c t 1 )( XXa T ij

Необходимость отбора дескрипторов • Проблема мультиколлинеарности дескрипторов и сингулярности матрицы (XT X)-1 • Проблема переопределенности моделей • Внесение «шума» в модель нерелевантными дескрипторами

Пошаговый вариант множественной линейной регрессии 2 2 22 12 2 1 )1()( R MNRR F ie INieie FFF max. Дескриптор включается в модель, если Дескриптор исключается из модели, если OUTieie. FFFmin Типичные значения порогов: F IN = 3. 84, F OUT = 2.

Разбиение выборки на обучающую и контрольную PRSS S — сумма квадратов остатков при прогнозе Sj j Se. PRSS 2)( PSS S — дисперсия свойства y на контрольной выборке Sj j Syy. PSS 2)( PRMSE S — среднеквадратичная ошибка на прогнозе S S S N PRSS PRMSE PMAE S — средняя абсолютная ошибка на прогнозе , 1 Sj j S Se N PMAE Q 2 s — квадрат коэффициента корреляции на прогнозе S SS S PSS PRSSPSS Q

Процедура скользящего контроля (cross-validation) 1. При μ -кратном скользящем контроле исходная выборка разбивается на μ приблизительно равных частей 2. Каждая из этих частей по очереди объявляется контрольной выборкой 3. Для нее формируется обучающая выборка, состоящая из всех соединений из исходной выборки, в нее не входящих 4. По обучающей выборке строится регрессионная модель 5. По текущей контрольной выборке вычисляется сумма квадратов ошибок PRSSs и сумма абсолютных ошибок PSAEs 6. Пункты 2 -5 повторяются для всех μ частей

Процедура скользящего контроля – статистические показатели 1 k SCVk. PRSS 1 k SCVk. PSAE RMSE CV — среднеквадратичная ошибка прогноза N PRSS RMSECV CV MAE CV — средняя абсолютная ошибка прогноза N PSAE MAECV CV Q 2 CV – коэффициент корреляции для прогноза SS PRSSSS QCV CV