Презентация ТВ часть 2 от О.А. Пекарской

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Случайная величина – это числовая характеристика случайного события. Например, выигрыш в лотерее – случайное событие. размер выигрыша – случайная величина.

Случайные величины обозначаются греческими буквами: (кси), (эта) , (тета) и так далее, а их возможные значения – латинскими буквами с индексами: x i , y i , z i. Например, случайная величина — «размер выигрыша в лотерее» может иметь следующие возможные значения : х 1 = 0 руб. ; х 2 = 10 руб. ; х 3 = 100 руб. ; х 4 = 1000 руб.

Случайные величины делятся на дискретные; непрерывные. Случайную величину называют дискретной , если множество ее возможных значений образует конечную последовательность чисел. (например, случайная величина — «размер выигрыша в лотерее» )

Непрерывные случайные величины сплошь заполняют некоторый числовой интервал. Например, время безотказной работы прибора теоретически [0 ; , + )

Дискретные случайные величины задаются рядом распределения , а непрерывные – функцией распределения

Ряд распределения ставит в соответствие каждому возможному значению случайной величины хi соответствующую вероятность рi. ξ x 1 x 2 … x n p i p 1 p 2 … p n i ipp i , i=1, 2, =

Пример 1 Рассмотрим случайную величину — «число гербов, выпавших при подбрасывании монеты три раза» . Она может принять четыре значения: 0, 1, 2, 3. P(A 0 )=1/8 ; P(A 1 )= 1 /8 +1/8=3/8; P(A 2 )= 1 /8 +1/8=3/8; P(A 3 )=1/8. ξ 0 1 2 3 p i 1/8 3/8 1/8 Построим ряд распределения случайной величины

Функцией распределения F( х ) СВ ξ называется функция действительного аргумента х , определенная на всей числовой оси и равная вероятности того, что СВ ξ примет значение меньше или равное х: F ( x ) = P ξ x }.

Пример Построить функцию распределения числа гербов при трех подбрасываниях монеты ξ 0 1 2 3 p i 1/8 3/8 1/8 Решение — <x< 0 : F(X)=P( ξ <0)=0 0 x< 1 : F(X)=P( ξ <1)= P( ξ =0)=1/8 1 x<2 : F(X)=P( ξ < 2 )=P( ξ =0) + P( ξ = 1) =1/8 +3/8=4/8 2 x< 3 : F(X)=P( ξ < 3 )= P( ξ =0) + P( ξ = 1)+ P( ξ = 2) = =1/8 +3/8=7/

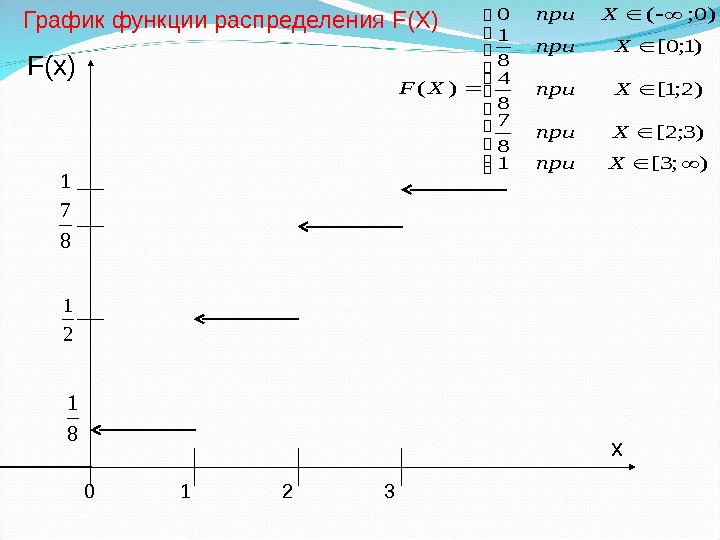
8 7 2 1811F(x)График функции распределения F(X) 0 1 2 3 х ); 3[1 )3; 2[ 8 7 )2; 1[ 8 4 )1; 0[ 8 1 )0; (0 )( Хпри Xпри X

Свойства функции распределения 1) 2) F(x) – неубывающая : если то F ( x 1 ) F ( x 2 ). 3) )()(}{a. Fba. P 1)(0x. F ; 0)(F 1)(F , 21xx 4) Вероятность попадания СВ в интервал ( a , b ] :

Пример СВ задана функцией распределения 41 40 4 00 )( Xпри. X Xпри XF Найти вероятность того, что в результате эксперимента случайная величина попадет в интервал (1; 3 ]. )()(}{ a. Fba. P 2 1 4 2 4 1 4 3 )1()3(}31{FFP

Самостоятельная работа Функция распределения Вариант ответа A B C D 1 / 9 1/3 1/2 1 21 20 2 00 )( Xпри. X Xпри XF Задание. Случайная величина задана функцией распределения. Найти вероятность попадания в интервал (1; 2 ].

Сверим ответы? 21 20 2 00 )( Xпри XF )()(}{a. Fba. P 2 1 2 2 )1()2(}21{FFP У нас a=1; b= 2. Тогда

Плотность распределения вероятностей)()( / x. Fxf xdttfx. F)()( Справедливо и обратное соотношение:

Свойства плотности распределения вероятностей 1) Для всех x плотность распределения вероятностей неотрицательна 2) Свойство нормировки b a dxxfba. Р )( 1)( dxxf . 0)(xf 3) Вероятность попадания случайной величины в интервал ( a ; b] равна

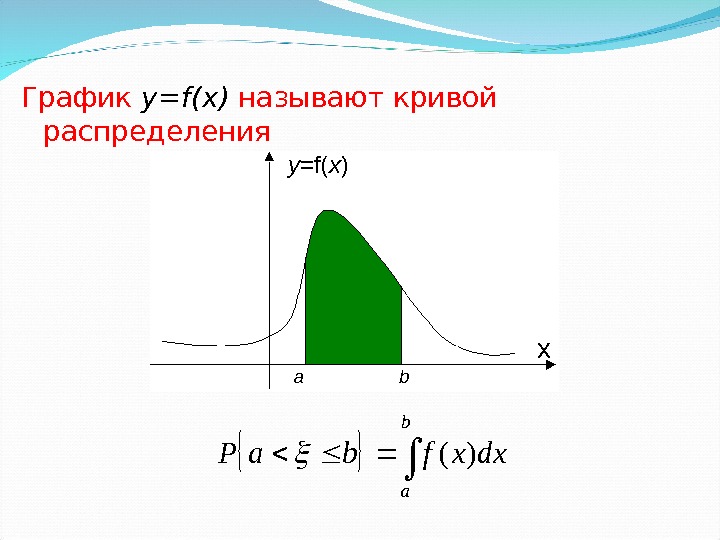
График y = f ( x ) называют кривой распределения y =f( x ) a b х b a dxxfba. Р )(

Пример Случайная величина задана плотностью вероятности 60 61 51 10 )( Xпри xf Найти вероятность того, что в результате эксперимента случайная величина попадет в интервал (3; 5 ]. b a dxxfba. Р )( 5 2 3 51 51 53 5 35 35 3 xdxdx. Р

Числовые характеристики СВ Это числа, полученные по определенным правилам из законов распределения. Наиболее часто используются: Математическое ожидание; Дисперсия; Среднеквадратическое (стандартное) отклонение.

Математическое ожидание СВ Характеризует среднее значение СВ Математическим ожиданием дискретной СВ называется сумма произведений возможных значений x i на их вероятности pi M ( ) = x 1 p 1 + x 2 p 2 +… x n p n

M ( ) = x 1 p 1 + x 2 p 2 +… x n p n Пример Найти математическое ожидание числа очков при одном подбрасывании игрального кубика. Решение 1. Строим ряд распределения 2. Вычисляем математическое ожидание ξ 1 2 3 4 5 6 p 1/6 1/6 1/65, 3 2 7 6 21 6 654321 6 6 1 5 6 1 4 6 1 3 6 1 2 6 1 1)( M

Математическим ожиданием M ( ) непрерывной случайной величины с плотностью вероятности называется интеграл , ( )М xf x dx )(xf Пример Найти математическое ожидание СВ, заданной плотностью вероятности 60 61 51 10 )( Xпри xf

1 6 0 51 0)()( dxxdxxxf. М Решение 6 2 6 1 11 1 36 1 35 ( ) 0 0 36 3, 5 5 5 2 10 10 10 x М xdx

Дисперсия случайной величины Дисперсия и среднеквадратическое отклонение определяют среднюю величину разброса значений СВ относительно математического ожидания Дисперсией случайной величины называется математическое ожидание квадрата СВ — M ( ): D ( )= M[ — M ( ) ]2 или D ( )= M[ — M ( ) ]2 Среднеквадратическое отклонение : )()(

Дисперсия непрерывной СВ определяется формулойdxxfmx. D)()()( 2 22 ( ) ( )D x f x dx M или i n i ip. Mx. D 0 2 ))(()( Для дискретной СВ дисперсия определяется по формуле или 2 11 2)( n i iipxpx.

Пример Найти дисперсию числа очков при одном подбрасывании кубика. ξ 1 2 3 4 5 6 p 1/6 1/6 1/6 9166, 2 12 35 )5, 3(]654321[ 61 )( 2222222 D Решение M ( ) = 3, 5 ( ) 2, 9166 1,

Пример Найти дисперсию случайной величины, заданной плотностью вероятности 60 61 51 10 )( Xпри xf 1 6 2 2 2 1 6 3 6 1 1 D( ) ( ) 0 0 3, 5 5 215 12, 25 2, 05 15 15 x f x dx М x dx x Решение ( ) 3, 5М

Нормальный закон распределения СВ Случайная величина ξ имеет нормальное распределение , если ее плотность распределения вероятностей при всех x задается равенством 2 2 ( ) 2 1 ( ) 2 x m f x e Нормальное распределение используется для описания случайных явлений, в которых на результат измерения влияет большое число независимых случайных факторов. Основные законы распределения СВ

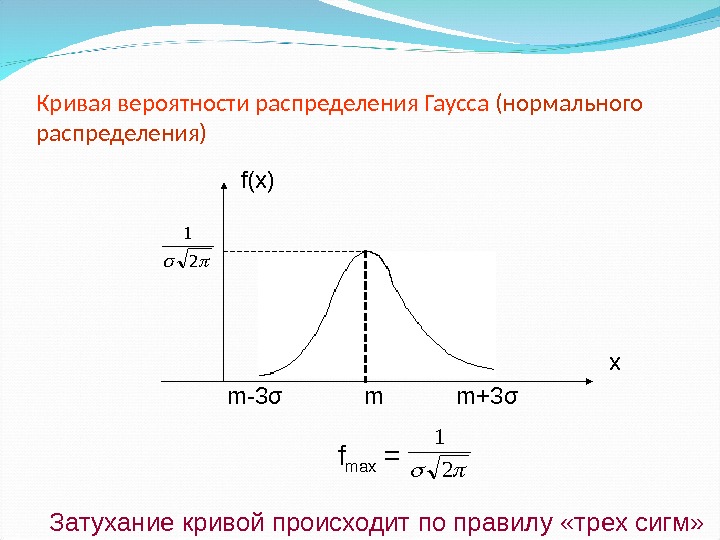
Кривая вероятности распределения Гаусса (нормального распределения)2 1 f(x) x mm-3 σ m+3 σ f max = 2 1 Затухание кривой происходит по правилу «трех сигм»

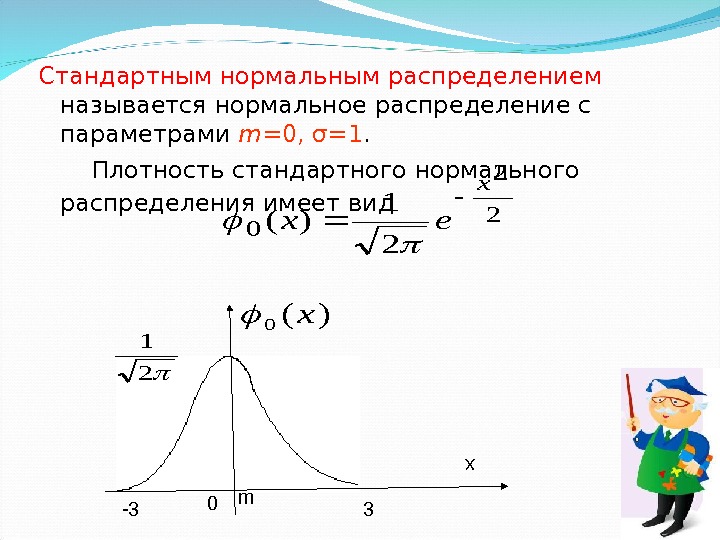
Стандартным нормальным распределением называется нормальное распределение с параметрами m = 0, σ=1. Плотность стандартного нормального распределения имеет вид 2 2 0 2 1 )( x ex 0 m -3 3 x )(0x

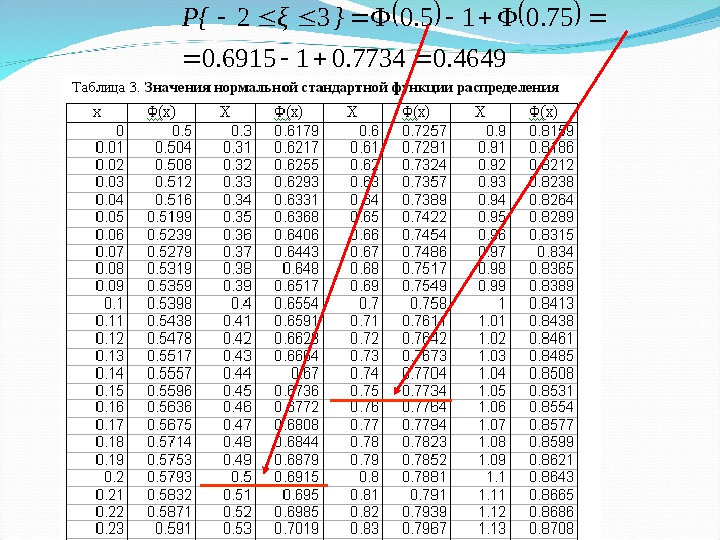
Функцию распределения стандартного нормального закона называют функцией Лапласа Для функции распределения стандартного нормального закона имеются таблицы значений, которые широко используются в статистических исследованиях dtex t 2 2 2 1 (x) 1. ( ) x m F x 2. ( ) 1 ( ) x x Свойства нормального распределения 3. b m a m P{aξ b} F(b) — F(a)

Пример Случайная величина задана плотностью вероятности 32 122 π32 1 )( хх еxf Определить: математическое ожидание; дисперсию; стандартное отклонение ; вероятность попадания значений случайной величины в интервал (-2; 3].

Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение ; вероятность попадания значений случайной величины в интервал (-2; 3]. 22 1 321 ( ) 32π х х еf x 32 122 π32 1 )( хх еxf 2 2 ( ) 21 ( ) 2 x m f x e

Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение ; вероятность попадания значений случайной величины в интервал (-2; 3]. 242 2)1( 216 )122( 32 122 π24 1 π216 1 π32 1 )( ххххх еееxf 32 122 π32 1 )( хх еxf 2 2 ( ) 21 ( ) 2 x m f x e

Пример Случайная величина задана плотностью вероятности Определить: математическое ожидание; дисперсию; стандартное отклонение ; вероятность попадания значений случайной величины в интервал (-2; 3]. 242 2)1( 216 )122( 32 122 π24 1 π216 1 π32 1 )( ххххх еееxf M( ξ )=1 ; σ ( ξ )=4; D( ξ )= σ 2 =16 32 122 π32 1 )( хх еxf 2 2 ( ) 21 ( ) 2 x m f x e

a =-2; b =3 3 1 2 3 3 2 4 4 2 3 0. 5 0. 75 0. 5 1 0. 75 4 4P{ ξ } F( ) — F( ) b m a m P{aξ b} F(b) — F(a)

4649. 07734. 016915. 0 75. 015. 032 }ξP{

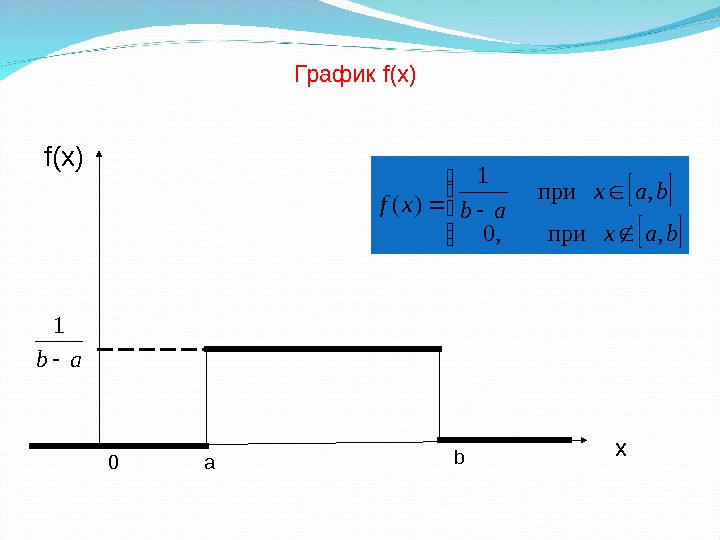
bax abxf , при , 0 , при 1 )(Случайная величина ξ распределена равномерно на промежутке [ a , b ], если ее плотность распределения вероятностей задается равенством Равномерное распределение

f(x) График f( х ) 0 х bax abxf , при , 0 , при 1 )( a bab

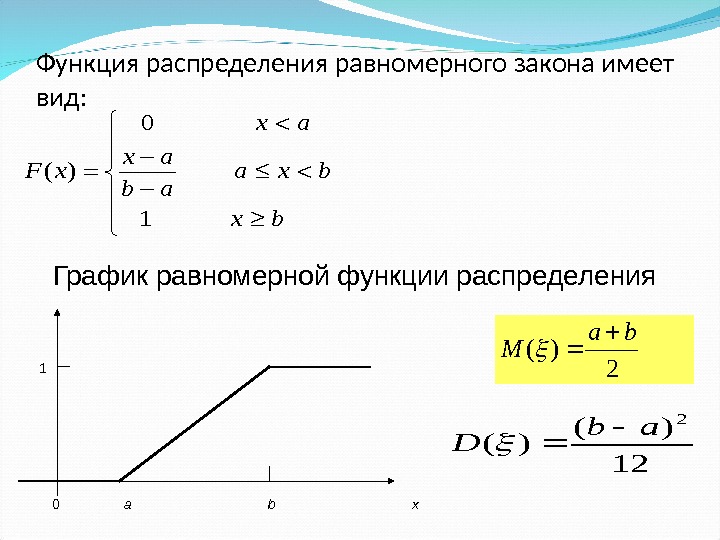
Функция распределения равномерного закона имеет вид: 0 ( ) 1 x a F x a x b b a x b 0 a b x 1 График равномерной функции распределения 12 )( )( 2 ab D 2 )( ba M

Вероятность того, что случайная величина η (число «успехов» при n независимых испытаниях) примет значение m , можно найти по формуле Бернулли Биномиальное распределение { } m m n. P m С p q Математическое ожидание и дисперсия случайной величины η равны M ( η )= n∙p ; D ( η )= n∙p∙q

Пример В коробку сложили 3 изделия. Вероятность, что изделие — бракованное, равна 0, 1. Найти математическое ожидание и дисперсию случайной величины — число бракованных изделий в коробке. Решение n= 3; р=0, 1; q=0, 9 M ( η )= n∙p ; D ( η )= n∙p∙q. M ( η ) = n∙p = 3 ∙ 0, 1=0, 3 D ( η )= n∙p∙q = 3 ∙ 0, 1 ∙ 0, 9 = 0,

Случайная величина ξ имеет показательное распределение с параметром , 0 если ее плотность распределения вероятностей задается равенством , при 0 ( ) 0, при 0 x e x f x x Показательное распределение 1 )(M 2 1 )( DФункция распределения показательного закона имеет вид: 0 если , 1 0 если , 0 )( xe x x. Ft

Пример Случайная величина задана функцией распределения 51 10 2 2, 01 )( M 25 1 04, 01 )( 2 D . 1 , 0 при 0 )(x e x x. FМатематическое ожидание этой случайной величины равно 0, 2, дисперсия равна 0, 04. Найти параметр λ. Решение λ =5 Проверка λ =