Презентация power

ОПРЕДЕЛЕНИЕ SIN, COS, TG, CTG Синусом угла α называется отношение ординаты точки В к R. Косинусом угла α называется отношение абсциссы точки В к R. Тангенсом угла α называется отношение ординаты точки В к ее абсциссе. Котангенсом угла α называется отношение абсциссы точки В к ее ординате. αR B (x; y)y x

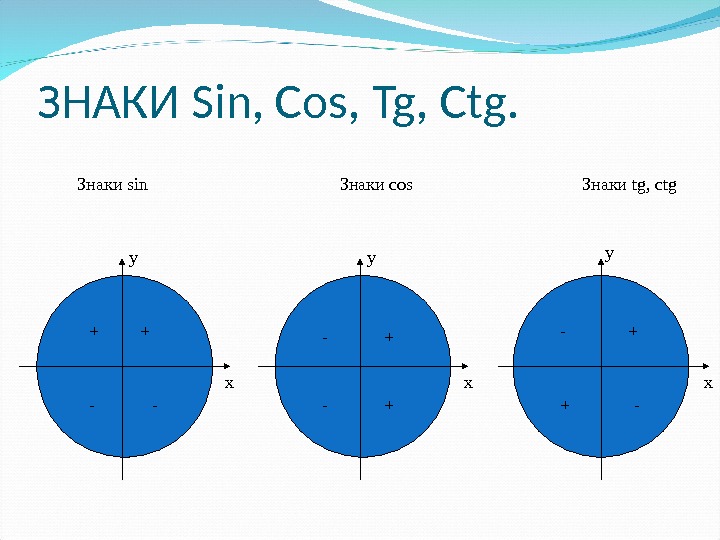
ЗНАКИ Sin, Cos, Tg, Ctg. xx xy y y. Знаки sin Знаки cos Знаки tg, ctg + + — — — ++ — + + —

РАДИАННАЯ МЕРА УГЛА 1 рад = (180/ пп )) 00 ≈ 57 00 Угол в один радиан – это угол поворота, при к-м конец начального радиуса описывает дугу, длина к-й равна радиусу. 1 рад. В А n n рад = (n*180 00 )/)/ пп nn 00 = = (( n*n* п)/

ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ Sin 22 a + cos 22 a = 1 Tg a = sin a / cos a Ctg a = cos a / sin a Tg a * ctg a = 1 Sin 22 a / cos 22 a = 1 / cos 22 a a 1 + ctg 22 a = 1 / sin 22 a a Cos 22 a = 1 – sin 22 a a

ФОРМУЛЫ ПРИВЕДЕНИЯ Тригонометрические функции углов вида (п/2) k k ± a± a , где k – Z, могут быть выражены через функции угла а с помощью формул, к-е называют формулами приведения. . Sin ( п/2 + а) = cos a Cos a ( п/2 + а) = — sin a Sin ( п/2 — а) = cos a Cos a ( п/2 — а) а) = = sin a Sin ( пп — — а) = sin a Cos a ( п п — а) а) = = — cos a Sin (2 пп — — а) = — sin a. Sin (2 пп + + а) = sin a Cos a ( 22 п п — а) а) = = cos a Cos a ( 22 п п ++ а) а) = = cos a Tg ( п/2 + а) = — ctg a Ctg ( п + а) = ctgctg

ФОРМУЛЫ СЛОЖЕНИЯ Косинус разности (суммы) 2 -х углов равен произведению косинусов этих углов плюс (( минус) произведение синусов этих углов. Cos (a- (+)(+) b) = cos a cos b + (-)(-) sin a sin b Синус суммы (разности) двух углов равен произведению синуса первого угла на косинус второго (минус) плюс произведению косинуса первого угла на синус второго. Sin (a + (-)(-) b) = sin a cos b + (-)(-) cos a sin b Tg (a + b) = (tg a +tg b) / (1 – tg a tg b)

ФОРМУЛЫ ДВОЙНОГО УГЛА Sin 2 a = 2 sin a cos a Cos 2 a = cos 22 a – sin 22 a a Tg 2 a = ( 2 tg a) / (1 – tg 22 a) a) 1 – cos 2 a = 2 sin 22 a a 1 + cos 2 a = 2 cos 22 a a Ctg (a + b) = (ctg a ctg b -1) / (ctg a + ctg b)

ФОРМУЛЫ СУММЫ И РАЗНОСТИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИИЙ Sin a + (-)(-) sin b = 2 sin ((a + (-)(-) b)/2) cos ((a – (+)(+) b)/2) Cos a + cos b = 2 cos ((a + b)/2) cos ((a – b)/2) Cos a – cos b = — 2 sin ((a + b)/2) sin ((a – b)/2)