Презентация OSNOVI_TEORIYi_AVTOMATIChNIKh_SISTEM_UPRAVLINNYa

ОСНОВИ ТЕОРІЇ АВТОМАТИЧНИХ СИСТЕМ УПРАВЛІННЯ Поняття про передаточні функції і частотні характеристики лінійних систем План. 1. Загальні відомості 2. Статичні характеристики АСР. 3. Перетворення Лапласа, передаточна функція, частотні характеристики 4. Типові ланки, їх диференційні рівняння та частотні характеристики.

Рис. 1. Статичні характеристики: 1 – лінійна; 2 — нелінійна

• Передаточний коефіцієнт k є основним параметром, який характеризує роботу системи або ланки в сталому режимі, і визначається із статичної характеритики . • При послідовному з’єднанні ланок • При паралельному з’єднанні ланок • Для ланок, охоплених зворотнім зв’язком x y k nkkkk. . . 21 ЗЗP P kk k k.

х х х( t) t 1( t ) t Типові зовнішні дії: а – одинична; б – гармонічна

Перетворення Лапласа Прикладpt etxpx 0 )()( )( 32 22 2 1 вхвх вихвихвих U dtd. U Tk. U dtd. U T dt Ud T )()1(32 22 1p. Up. Tkp. Up. Tвхвих

• Передаточна функція W (р) – відношення зображення вихідної величини ланки до зображення вхідної. • Якщо замінити р на j , то отримаємо частотну передаточну функцію )( )( )( px py p. W )( )( )( jx jy j. W

Амплітудо-частотна характеристика – залежність відношення амплітуди Авих( і) коливань гармонічної дії на виході до амплітуди Авх( і) коливань на вході від частоти коливань і Фазо-частотна характеристика – залежність кута зсуву фаз від частоти Амплітудо-фазо-частотна характеристика – залежність передаточної функції від частоти)(іf. К)( )( )( івх івих і А А К )(if

Безінерційна (підсилювальна) • (к – передаточний коефіцієнт)kxy )()(рkxрy k px py p. W )( )( )(

Аперіодична ланка І порядку kxy dx dy T )()()1(pkxpy. Tp Tp k px py 1)( )( W(p)=

Аперіодична ланка ІІ порядку (послідовне з’єднання двох аперіодичних ланок першого порядку за умови Т 1 2Т 2)kxy dt dy T dt yd T 1 22 2 2 )()()1( 122 2pkxpyp. T 1)( )( 1 22 2 p. T k px py W(p)=

Диференціююча dt dx ky )()(pkpxpy kp px py )( )( Ідеальна W(p)= dt dx k. Ty dx dy T)()()1(pk. Tpxpy. Tp Tp k. Tp px py 1)( )( Реальна W(p)=

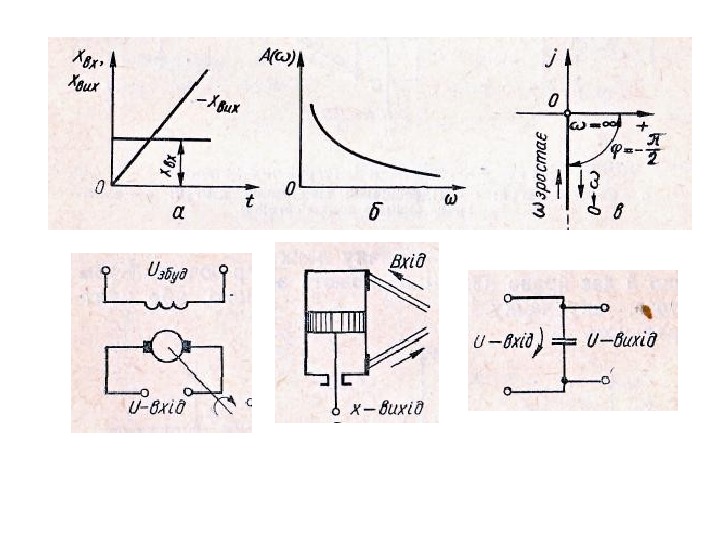
Інтегруюча dttxkty t 0 )()( )(tkx dt dy T )()(pkxp. Tpy Tp k px py p. W )( )( )(

Коливальна kxy dx dy T)()()1(pkxpy. Tp Tp k px py 1)( )( Стійка W(p)= kxy dt dy T dt yd T 1 22 2 2)()()1( 122 2pkxpyp. T 1)( )( 1 22 2 p. T k px py. Нестійка W(p)=

kxy dt yd T 2 2 )()()1(22 2pkxpyp. T 1)( )( 22 2 p. T k px py Консервативна W(p)=

Запізнювальна )()(txty )()(pxepy p p e px py )( )( W(p)=