Презентация Лекция No. 4 МА — НБ

профессор Резниченко Александр Васильевич Москва – 2013 Раздел 2 тема № 3 «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ» Лекция № 11 Российская академия народного хозяйства и государственной службы при Президенте РФ Факультет национальной безопасности

УЧЕБНЫЕ ВОПРОСЫ: 1. 1. Понятия первообразной и неопределенного интеграла 2. Свойства неопределенного интеграла 3. Методы интегрирования

Литература 1. «Высшая математика для экономических специаль-ностей» . Учебник и Практикум (части I и II) / Под ред. Н. Ш. Кремера. М. : Высшее образование, 2008. 2. «Математика: Математический анализ. Дифференци-альные уравнения. Теория вероятностей. Математи-ческая статистика» . Учебно-методическое пособие / Под ред. А. Н. Данчула. М. : Изд-во РАГС, 2004. 3. Гельман В. Я. «Решение математических задач сред-ствами Excel : Практикум» . Учебник для вузов. СПб. : ПИТЕР, 2003. 4. «Сборник задач по математике» . М. : Изд. РАГС, 2005.

Понятия первообразной и неопределенного интеграла ПЕРВЫЙ ВОПРОС

Понятие производной FF » ( xx ) действительной функции одного действительного переменного xx с геометрической точки зрения соответствует угловому коэффициенту касательной к графику этой функции. Если функция задает зависимость пройденного пути от времени, то производная этой функции является скоростью движения. Имеет смысл и обратная задача –– восстановление функции FF ( xx ) по известной зависимости ее производной FF » ( xx ) = ff ( xx ) от аргумента xx. . Геометрически решение этой задачи означает построение графика функции FF ( xx ) , для которой функция ff ( xx ) задает изме-нение углового коэффициента касательной к графику уу = FF ( xx ) при изменении xx. В механике поставленная задача возникает при нахождении пройденного пути ss ( tt ) по известной зависимости скорости vv ( tt ) движения от времени tt. Определение. Функцию FF ( xx ) называют первообразной функции ff ( xx ), опре — деленной в некотором промежутке XX (на отрезке, в конечном или бесконечном интервале или полуинтервале), если FF ( xx ) диффе — ренцируема в этом промежутке и xx XX значение производной FF » ( xx ) совпадает со значением функции ff ( xx ), т. е. FF » ( xx ) = ff ( xx ) xx XX (или d. F ( xx ) = ff ( xx ) dxdx xx XX ). Замечание. Если XX = [ аа , bb ], то под дифференцируемостью функции в гра — ничных точках xx = аа , xx = bb отрезка понимают существование конечных правосторонней и левосторонней производных соответственно. Пример. . Функция FF ( xx ) = xx 33 на всей числовой прямой RR является перво — образной функции ff ( xx ) = FF » ( xx ) = З хх 22.

Замечание. Если функция ff ( xx ) имеет первообразную, то эта первообразная не единственна. Пример. . Для функции ff ( xx ) = З хх 22 первообразными будут и функции xx 33 +1, xx 33 — 2 и вообще xx 33 + СС , где СС – произвольное постоянное число, поскольку ( xx 33 + СС )’ = З хх 22 = ff ( xx ). Геометрическая иллюстрация Если построен график первообраз-ной уу = FF ( xx ) функции ff ( xx ), то графики всех остальных первообразных получаются параллельным сдвигом этого графика вдоль оси ординат вверх или вниз на произвольное расстояние СС.

Теорема. Дифференцируемые в промежутке XX функции FF ( xx ) и ФФ ( хх ) будут в этом промежутке первообразными одной и той же функции ff ( xx ) тогда и только тогда, когда разность их значений для любого хх из промежутка XX постоянна: FF ( xx ) – ФФ ( хх ) = СС = const xx XX. Доказательство. 1. 1. Если FF ( xx ) – некоторая первообразная функции ff ( xx ) в проме-жутке XX , то, согласно определению, FF ‘ ( xx ) = ff ( xx ) xx XX. Но тогда и функция ФФ ( хх ) = FF ( xx ) – СС ( СС = const ) также является первообразной функции ff ( xx ) в этом промежутке, поскольку ФФ ‘( хх ) = ( FF ( xx ) – СС )’ = FF ‘( xx ) = ff ( xx ) xx XX . 22. Введем φφ ( хх ) = FF ( xx ) – ФФ ( хх ) и найдем ее производную φφ ‘( хх ) = ( FF ( xx ) – ФФ ( хх ))’ = FF ‘( xx ) – ФФ ‘( хх ) = ff ( xx ) – ff ( xx ) = 0 xx XX. Но в силу признака постоянства дифференцируемой функции, вытекающего из теоремы Лагранжа , равенство φφ ‘( хх ) = 0 xx XX означает, что φφ ( хх ) = FF ( xx ) – ФФ ( хх ) = СС = const xx XX. Описывает ли выражение FF ( xx ) + СС все первообразные функции для ff ( xx ) ? ?

Определение. Множество всех первообразных функции ff ( xx ) в некотором промежутке ХХ называют неопределенным интегралом от этой функции в данном промежутке и обозначают ∫ ff ( xx ) dxdx. При этом символ ∫ именуют знаком интеграла , ff ( xx ) – подынтегральной функцией , ff ( xx ) dxdx – подынтегральным выражением , xx – переменной интегрирования. Если FF ( xx ) – какая-либо первообразная функции ff ( xx ) в проме-жутке ХХ , то правомерна запись: где СС – произвольная постоянная величина, называемая обычно постоянной интегрирования. Определение. Операция нахождения неопределенного интеграла от некото-рой функции называется интегрированием этой функции. или )()( Cx. Fdxxf , )()( Cx. Fdxxf

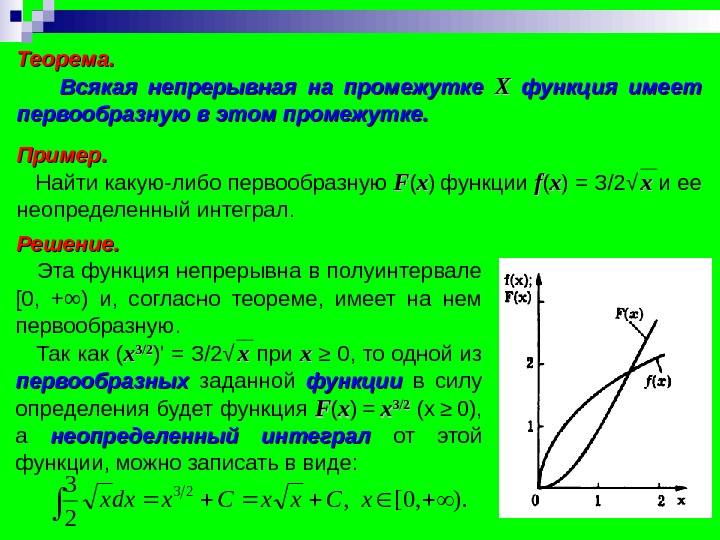
Теорема. Всякая непрерывная на промежутке XX функция имеет первообразную в этом промежутке. Пример. Найти какую-либо первообразную FF ( xx ) функции ff ( xx ) = З/2 √ хх и ее неопределенный интеграл. Решение. Эта функция непрерывна в полуинтервале [0, + ∞ ) и, согласно теореме, имеет на нем первообразную. Так как ( хх 3/23/2 )’ = З/2 √ хх при хх ≥ 0, то одной из первообразных заданной функции в силу определения будет функция FF ( xx ) = хх 3/23/2 (х ≥ 0), а неопределенный интеграл от этой функции, можно записать в виде: ). , 0[ , 2 3 23 x. Cxdxx

Свойства неопределенного интеграла ВТОРОЙ ВОПРОС

Основные свойства неопределенного интеграла Пусть для функции ff ( xx ), определенной в некотором промежутке ХХ , в этом промежутке существуют первообразная FF ( xx ) и неопре-деленный интеграл. 1. 1. Производная неопределенного интеграла равна подын-тегральной функции , т. е. 2. 2. Дифференциал неопределенного интеграла равен под-ынтегральному выражению , т. е. По определению дифференциала ). ()()())(( xf. Cx. Fdxxf . )())(( dxxfd . )()())(( dxxfdx. Cx. Fdxxfd

Основные свойства неопределенного интеграла 3. 3. Неопределенный интеграл от дифференциала функ-ции FF ( xx ) равен этой функции с точностью до константы: Интегрирование и дифференцирование являются взаимно обратными операциями. 4. Постоянный множитель можно выносить за знак нео-пределенного интеграла , т. е. Рассмотрим. )())( Rdxxf. )()()( dxxfxg . )(: и 0)()( )()()( Сxg. Сxfxf d хxfdxxfdxxfxg . )()(RСCx. Fxd. F. )())( Сdxxf

Основные свойства неопределенного интеграла 5. 5. Неопределенный интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций : Замечание. Свойство 55 остается справедливым и для любого конечного числа слагаемых. Замечание. Обобщая свойства 44 и 55 , можно сделать вывод, что неопреде-ленный интеграл от нетривиальной линейной комбинации функций равен такой же линейной комбинации неопределен-ных интегралов от каждой из этих функций. Использование этого свойства линейности при интегриро-вании иногда называют методом разложения. . )()())()(( ( dxxgdxxfdxxgxf

Основные свойства неопределенного интеграла 6. 6. Пусть в промежутке XX определена сложная функция ff ( uu ( xx )), а функция tt = uu ( xx ) дифференцируема в этом промежутке. Е c ли функция ff ( tt ) имеет в промежутке ТТ uu ( ХХ ) первообраз-ную FF ( tt ), то d. F ( tt ) = ff ( tt ) dtdt и справедливо свойство инвариант-ности неопределенного интеграла в виде: Замечание. Данное свойство позволяет свести вычисление неопределен-ного интеграла от функции gg ( хх ) к следующей процедуре: — представить gg ( хх ) в виде ff ( uu ( xx )) uu ‘( xx ); — найти первообразную FF ( uu ) функции ff ( uu ): Использование этого свойства при нахождении неопределен-ного интеграла носит название метода интегрирования подведением под знак дифференциала. . ))(()())(( Cxu. Fxduxuf . ))(()())(()( (( Cxu. Fxduxufdxxg

Интегралы от элементарных функций ); 0( ln ); 0( ln 2 1 ; ; ln ); 0: ( ||ln ); 1( 1; 0 2 2 22 1 a. Caxx ax dx a. C ax ax aax dx Cedxe C aa dxa Xx. XCx xdx n. C n x dxx Cdx xx x x n n ). 0( arctg 1 ); ; 0( arcsin ; ctg sin ; tg cos ; sincos ; cossin 22 2 a C a x axa dx axaa C a x xa dx Cx xdx Cxxdx

Основные свойства неопределенного интеграла Пример. Найти интеграл Решение. Преобразуем функцию и тогда . 3 dxx. 4 3 3 4 34 34 31 3 Cx. C x dxxdxx. 19 2 x dx 2 22 311 91 19 1 xx. 13 13 ln 6 1 3 1 ln 2 3 9 1 3 19 1 19 2 2 2 C x x x dx

Методы интегрирования ТРЕТИЙ ВОПРОС

dx xxxx dx xx 2 cos 2 sin 22 2. cos sin)sin 1( Cxxdxxdxdxx Метод разложения Неопределенный интеграл от нетривиальной линейной комбинации функций равен такой же линейной комбинации неопределенных интегралов от каждой из этих функций. Пример. Найти интеграл Решение. . 2 cos 2 sin 2 dxxx Методы интегрирования. 2162 dx xx dxxxxdx x xxx dx xx )824( 2 )4)(2)(2( 216 21 23 2. 8 38 5 2 824 2 23 25 21 23 Сххxxdxdxxdxxdxx

Методы интегрирования Метод замены переменой Один из основных методов интегрирования – метод замены переменной (( метод подстановки )) , описывается следующей формулой : Пример. Найти интеграл Решение. Пусть tt = 1 – 2 xx , тогда а. )())(()( (dtttfdxxf. 21 xdx. 21 dtdx , 21 21 tx . |2 -1|ln 2 1 |t|ln 2 12 1 21 Cx. C t dt x dx

Методы интегрирования Метод введения (подведения) под знак дифференциала Данный метод интегрирования является вариантом метода замены переменной, когда новая переменная в явном виде не вводится. Пример. Найти интеграл Решение. Используя свойства дифференциала, получаем. )23 cos( dxx ). ( 212 xdxdx . 21 )( 21 2222 22 Cexdexdedxxexxxx . 2 dxxe -x ). 23( 31 )3( 31 xdxddx. )23(sin 31 )23( cos 31 )23(cos Cxxdxdxx

Методы интегрирования Метод интегрирования по частям Пусть uu = uu ( xx ) и vv = vv ( xx ) – дифференцируемые функции, тогда формула называется формулой интегрирования по частям для не-определенного интеграла. Пример. Найти интеграл Решение. Пусть xx == uu и dxdx == dudu , а dvdv == ee — 22 xx , и тогда vduuvudv . 2 dxxe x dx. Cexdxxe xxx 222 2 1 Cev x 2 2 1. 4 1 2 1 2 1 1 22 Cexe. CCxe. Cxxe xxxx

Методы интегрирования Пример. Найти интеграл Решение. Пусть xx 22 = uu и 2 xdxxdx = dudu , а sinsin xx dxdx = dvdv и vv = — coscos xx , тогда, применяя формулу интегрирования по частям, имеем Полученный интеграл не является табличным, но степень переменной хх уменьшилась на единицу, тогда как второй сомножитель остался того же типа. Повторяем процедуру: xx = uu и dxdx = dudu , а coscos xx dxdx = dvdv и vv = = sinsin xx – . sin 2 xdxx . cos 2)cos(cossin 222 dxxxxxxdxx )sinsin(2 cossin 22 dxxxxxxxdxx. cos 2 sin 2 cos 2 Cxxxxx

Методы интегрирования Метод интегрирования рациональных выражений ( метод неопределенных коэффициентов ) Пусть PP ( xx )/ QQ ( xx ) – правильная дробь, т. е. степень числителя РР ( хх ) меньше степени знаменателя QQ ( xx ), а знаменатель QQ ( xx ) допускает разложение на линейные множители: где аа ii ≠ аа jj при ii ≠ jj и kk 11 , , . . . , kk ll – положительные целые числа. В этом случае дробь PP ( xx )/ QQ ( xx ) допускает представление в виде суммы простейших дробей: где – некоторые неизвестные числа. llk. AAA . . . , , ,

. 21 ; 43 ; 41 002 1 213 321 32 31 AAA AA AAПример. Найти интеграл Решение. Записывая подынтегральную функцию в виде суммы простейших дробей, имеем: Тождественное равенство получается при Методы интегрирования

Методы интегрирования Замечание. В случае, когда многочлен QQ ( xx ) не допускает разложения на линейные множители ( QQ ( xx ) имеет комплексные корни), в выра-жении PP ( xx )/ QQ ( xx ) дополнительно содержатся сомножители вида ( хх 22 + pxpx + qq ) mm , где mm > 0. Тогда разложение дроби PP ( xx )/ QQ ( xx ) дополнительно содержит слагаемые вида: Пример. Найти интеграл Решение. Разложение подынтегральной функции на простей-шие дроби имеет вид: Тождественное равенство получается при AA 1 1 = 1; NN 1 1 = 0; MM 1 1 = -1.

Методы интегрирования Простейшие интегралы от функций, содержащие иррацио-нальности , являются табличными, либо сводятся к табличным с использованием свойств интеграла и/или замены переменной. В более сложных случаях подход состоит в сведении искомого интеграла к интегралу от рациональной функции с помощью специальной замены переменной ( метод рационализации интеграла ). Интегралы вида где RR – рациональная функция, находятся соответственно с помощью подстановок

Методы интегрирования Пример. Найти интеграл Решение. Наименьшее общее кратное степеней 44 и 66 радика-лов, через которые записана подынтегральная функция, – 1212. Поэтому полагаем: tt = xx 1/12. Тогда xx = tt 1212 , dxdx = 12 tt 1111 dtdt и Далее

Методы интегрирования Интегралы вида ( RR – рациональная функция) допускают рационализацию ( метод интегрирования тригоно-метрических функций ) с помощью универсальной подстановки tt = tgtg ( xx /2) , где – ππ < х < ππ. Тогда Пример. Найти интеграл Решение. Для tt = tgtg ( xx /2) получаем …

Методы интегрирования Замечание. Использование универсальной подстановки tt = tgtg ( xx /2) при ин — тегрировании функции вида RR ( sinsin xx , coscos xx ) часто приводит к гро — моздким подынтегральным функциям. В частных случаях можно использовать другие подстановки: если RR (- uu , vv ) = — RR ( uu , vv ), то используется подстановка t t = coscos xx ; если RR ( uu , — vv ) = — RR ( uu , vv ), то используется подстановка tt = ss ii nn xx. Кроме того, могут использоваться формулы тригонометрии. Пример. Найти интеграл Решение. . cos 31 cos)(cos)cos 1( 32 Cxxxdx )(cos sinsin 23 xdxxdx. Замечание. Из правил дифференцирования следует, что производная произвольной элементарной функции вновь является эле-ментарной функцией. Операция нахождения первообразной ( неопределенного интеграла ) таким свойством не обладает – существуют элементарные функции, первообразные которых элементарными функциями уже не являются. Например, являются неберущимися в элементарных функциях , , а сами функции – неинтегрируемыми в конечном виде. xdx dx x x dxxdxex ln , sin ,

Благодарю за внимание, лекция окончена!