Презентация Лекция 4 Динамика вращательного движения full








































lekciya_4_dinamika_vraschatelynogo_dvigheniya_full.ppt
- Размер: 3.4 Mегабайта
- Количество слайдов: 60
Описание презентации Презентация Лекция 4 Динамика вращательного движения full по слайдам
















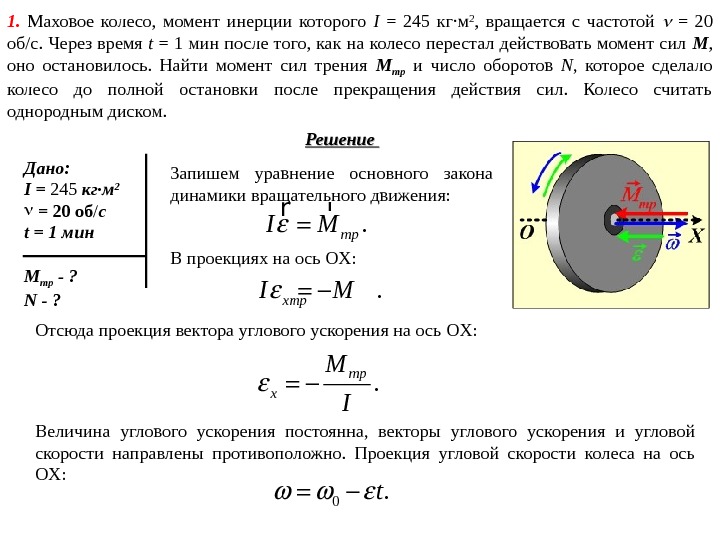
 1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. Дано: I = 245 кг·м 2 = 20 об / c t = 1 мин M тр — ? N — ? Решение Запишем уравнение основного закона динамики вращательного движения: . тр. I M r r В проекциях на ось OX : . x тр. I M Отсюда проекция вектора углового ускорения на ось OX : . тр x M I Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Проекция угловой скорости колеса на ось OX: 0. t
1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. Дано: I = 245 кг·м 2 = 20 об / c t = 1 мин M тр — ? N — ? Решение Запишем уравнение основного закона динамики вращательного движения: . тр. I M r r В проекциях на ось OX : . x тр. I M Отсюда проекция вектора углового ускорения на ось OX : . тр x M I Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Проекция угловой скорости колеса на ось OX: 0. t
 Колесо остановится, поэтому0 0. t Решение (продолжение) Величина (модуль) вектора углового ускорения: 0 , t 1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. 02 , 2. t . x тр. I M Для модулей векторов: 2. тр. M I I t 2 2 3, 14 20 245 513. 60 тр. M I Н м t
Колесо остановится, поэтому0 0. t Решение (продолжение) Величина (модуль) вектора углового ускорения: 0 , t 1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. 02 , 2. t . x тр. I M Для модулей векторов: 2. тр. M I I t 2 2 3, 14 20 245 513. 60 тр. M I Н м t
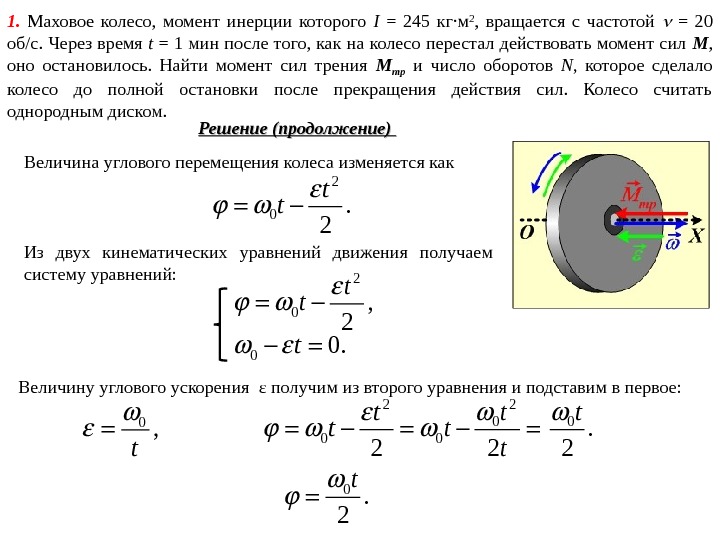
 Величина углового перемещения колеса изменяется как Решение (продолжение) Из двух кинематических уравнений движения получаем систему уравнений: 2 0, 2 t t 0 0. t Величину углового ускорения ε получим из второго уравнения и подставим в первое: 0 , t 2 2 0 0 0 2 2 tt t 0. 2 t 1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. 2 0. 2 t t 0. 2 t
Величина углового перемещения колеса изменяется как Решение (продолжение) Из двух кинематических уравнений движения получаем систему уравнений: 2 0, 2 t t 0 0. t Величину углового ускорения ε получим из второго уравнения и подставим в первое: 0 , t 2 2 0 0 0 2 2 tt t 0. 2 t 1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. 2 0. 2 t t 0. 2 t
 1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. Решение (продолжение) Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения: 0. 2 t 2 , N 02. После подстановки получим: 2 2. 2 t N Отсюда полное число оборотов колеса до остановки: 20 60 600. 2 2 t N Ответ: М тр = 513 H·м, N = 600.
1. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М , оно остановилось. Найти момент сил трения М тр и число оборотов N , которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. Решение (продолжение) Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения: 0. 2 t 2 , N 02. После подстановки получим: 2 2. 2 t N Отсюда полное число оборотов колеса до остановки: 20 60 600. 2 2 t N Ответ: М тр = 513 H·м, N = 600.
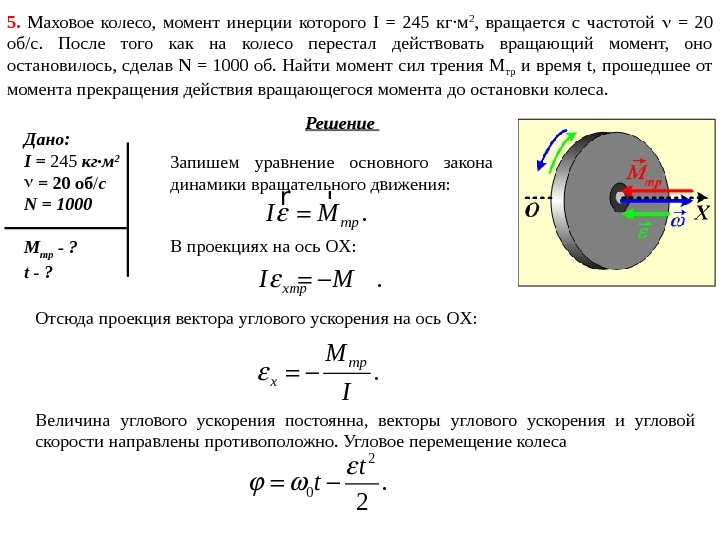
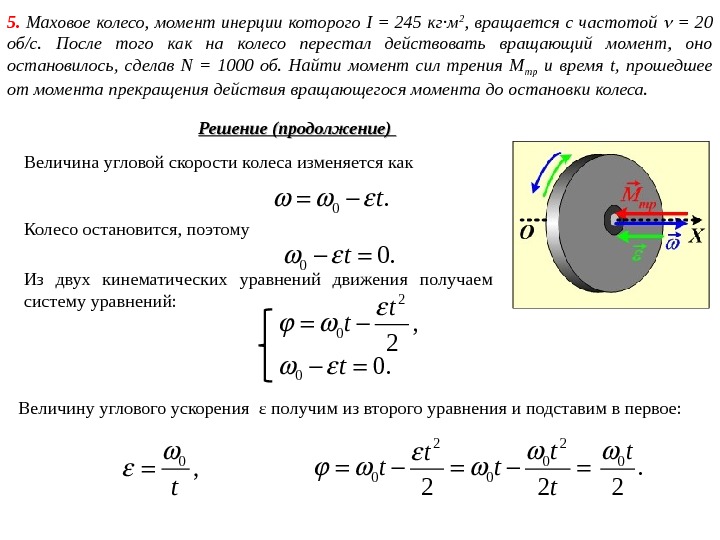
 5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Дано: I = 245 кг·м 2 = 20 об / c N = 1 000 M тр — ? t — ? Решение Запишем уравнение основного закона динамики вращательного движения: . тр. I M r r В проекциях на ось OX : . x тр. I M Отсюда проекция вектора углового ускорения на ось OX : . тр x M I Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Угловое перемещение колеса 2 0. 2 t t
5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Дано: I = 245 кг·м 2 = 20 об / c N = 1 000 M тр — ? t — ? Решение Запишем уравнение основного закона динамики вращательного движения: . тр. I M r r В проекциях на ось OX : . x тр. I M Отсюда проекция вектора углового ускорения на ось OX : . тр x M I Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Угловое перемещение колеса 2 0. 2 t t
 5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Величина угловой скорости колеса изменяется как 0. t Колесо остановится, поэтому 0 0. t Решение (продолжение) Из двух кинематических уравнений движения получаем систему уравнений: 2 0 , 2 t t 0 0. t Величину углового ускорения ε получим из второго уравнения и подставим в первое: 0 , t 2 2 0 0 0 2 2 tt t 0. 2 t
5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Величина угловой скорости колеса изменяется как 0. t Колесо остановится, поэтому 0 0. t Решение (продолжение) Из двух кинематических уравнений движения получаем систему уравнений: 2 0 , 2 t t 0 0. t Величину углового ускорения ε получим из второго уравнения и подставим в первое: 0 , t 2 2 0 0 0 2 2 tt t 0. 2 t
 5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения: Решение (продолжение) 0. 2 t 2 , N 02. После подстановки получим: 2 2. 2 t N 2 2 1000 100. 20 N t c Откуда время движения до остановки:
5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения: Решение (продолжение) 0. 2 t 2 , N 02. После подстановки получим: 2 2. 2 t N 2 2 1000 100. 20 N t c Откуда время движения до остановки:
 5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Решение (продолжение) Теперь вернёмся к динамическому уравнению движения и найдём величину момента сил трения. Для проекций на ось OX: Величина момента сил трения. x тр. I M . тр x. M I Или, для краткости, . тр. M I Как было получено ранее, 0 , t 2. N t 0 0 2 t N Теперь 2 2 N 2. N
5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Решение (продолжение) Теперь вернёмся к динамическому уравнению движения и найдём величину момента сил трения. Для проекций на ось OX: Величина момента сил трения. x тр. I M . тр x. M I Или, для краткости, . тр. M I Как было получено ранее, 0 , t 2. N t 0 0 2 t N Теперь 2 2 N 2. N
 5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Решение (продолжение) , тр. M I 2 , N 2 3, 14 400 245 308. 1000 тр M IН м N Ответ: t = 100 c; М тр = 308 H·м.
5. Маховое колесо, момент инерции которого I = 245 кг·м 2 , вращается с частотой = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения М тр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса. Решение (продолжение) , тр. M I 2 , N 2 3, 14 400 245 308. 1000 тр M IН м N Ответ: t = 100 c; М тр = 308 H·м.
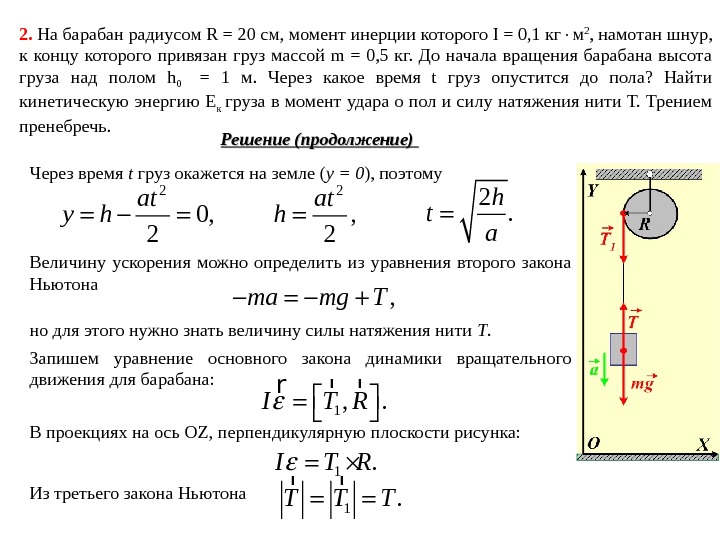
 2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Дано: m = 0, 5 кг I = 0, 1 кг·м 2 R = 20 cм h 0 = 1 м t — ? Е к — ? Т — ? Решение Прежде всего, запишем динамическое уравнение движения груза. Из второго закона Ньютона: . ma mg T r r r Для проекций на ось OY : . yma mg T Если учесть, что груз опускается, то, ma mg T где a — величина (модуль) проекции ускорения на ось OY. a = const. , начальная скорость груза равна нулю, следовательно кинематическое уравнение движения можно записать так: 2. 2 at y h
2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Дано: m = 0, 5 кг I = 0, 1 кг·м 2 R = 20 cм h 0 = 1 м t — ? Е к — ? Т — ? Решение Прежде всего, запишем динамическое уравнение движения груза. Из второго закона Ньютона: . ma mg T r r r Для проекций на ось OY : . yma mg T Если учесть, что груз опускается, то, ma mg T где a — величина (модуль) проекции ускорения на ось OY. a = const. , начальная скорость груза равна нулю, следовательно кинематическое уравнение движения можно записать так: 2. 2 at y h
 2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Решение (продолжение) Через время t груз окажется на земле ( y = 0 ), поэтому 20, 2 at y h 2, 2 at h 2. h t a Величину ускорения можно определить из уравнения второго закона Ньютона , ma mg T но для этого нужно знать величину силы натяжения нити T. Запишем уравнение основного закона динамики вращательного движения для барабана: 1 , . I T R r rr В проекциях на ось OZ, перпендикулярную плоскости рисунка: 1. I T R Из третьего закона Ньютона 1. T T T r r
2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Решение (продолжение) Через время t груз окажется на земле ( y = 0 ), поэтому 20, 2 at y h 2, 2 at h 2. h t a Величину ускорения можно определить из уравнения второго закона Ньютона , ma mg T но для этого нужно знать величину силы натяжения нити T. Запишем уравнение основного закона динамики вращательного движения для барабана: 1 , . I T R r rr В проекциях на ось OZ, перпендикулярную плоскости рисунка: 1. I T R Из третьего закона Ньютона 1. T T T r r
 2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Решение (продолжение) 1, I T R . I TR Величину углового ускорения ε можно выразить через величину линейного ускорения a: . a R Теперь можно записать систему уравнений, из которой можно определить a и T : , a I TR R . ma mg T 2 , TR a I 2, TR m mg T I 21 , m. R T mg I 2. I T mg I m. R
2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Решение (продолжение) 1, I T R . I TR Величину углового ускорения ε можно выразить через величину линейного ускорения a: . a R Теперь можно записать систему уравнений, из которой можно определить a и T : , a I TR R . ma mg T 2 , TR a I 2, TR m mg T I 21 , m. R T mg I 2. I T mg I m. R
 2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Решение (продолжение) 2 2 0, 1 0, 5 9, 8 4, 1 0, 5 0, 2 I T mg H I m. R 2 TR a I Найдём величину линейного ускорения a: 2 2 R I mg I I m. R 2 2. m. R g I m. R Подставим выражение для a в формулу для времени движения груза: 2 22 2. h h I m. R t a g m. R 2 22 2 1 0, 5 0, 2 1, 1. 9, 8 0, 5 0, 2 h I m. R t c g m. R
2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Решение (продолжение) 2 2 0, 1 0, 5 9, 8 4, 1 0, 5 0, 2 I T mg H I m. R 2 TR a I Найдём величину линейного ускорения a: 2 2 R I mg I I m. R 2 2. m. R g I m. R Подставим выражение для a в формулу для времени движения груза: 2 22 2. h h I m. R t a g m. R 2 22 2 1 0, 5 0, 2 1, 1. 9, 8 0, 5 0, 2 h I m. R t c g m. R
 2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Ответ: t = 1, 1 c; E k = 0, 82 Дж; Т = 4, 1 H. Решение (продолжение) Кинетическая энергия груза 2. 2 k mv E Скорость груза 2 2, m. R a g I m. R 2 2 2. h I m. R t g m. R , v atгде 2 2 2 k mv ma t E 22 2 2 m m. R h I m. R g m. R 2 2. m. R mgh I m. R 2 2 0, 5 0, 2 0, 5 9, 8 1 0, 82. 0, 1 0, 5 0, 2 k m. R E mgh. Дж I m. R
2. На барабан радиусом R = 20 см, момент инерции которого I = 0, 1 кг м 2 , намотан шнур, к концу которого привязан груз массой m = 0, 5 кг. До начала вращения барабана высота груза над полом h 0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Е к груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь. Ответ: t = 1, 1 c; E k = 0, 82 Дж; Т = 4, 1 H. Решение (продолжение) Кинетическая энергия груза 2. 2 k mv E Скорость груза 2 2, m. R a g I m. R 2 2 2. h I m. R t g m. R , v atгде 2 2 2 k mv ma t E 22 2 2 m m. R h I m. R g m. R 2 2. m. R mgh I m. R 2 2 0, 5 0, 2 0, 5 9, 8 1 0, 82. 0, 1 0, 5 0, 2 k m. R E mgh. Дж I m. R
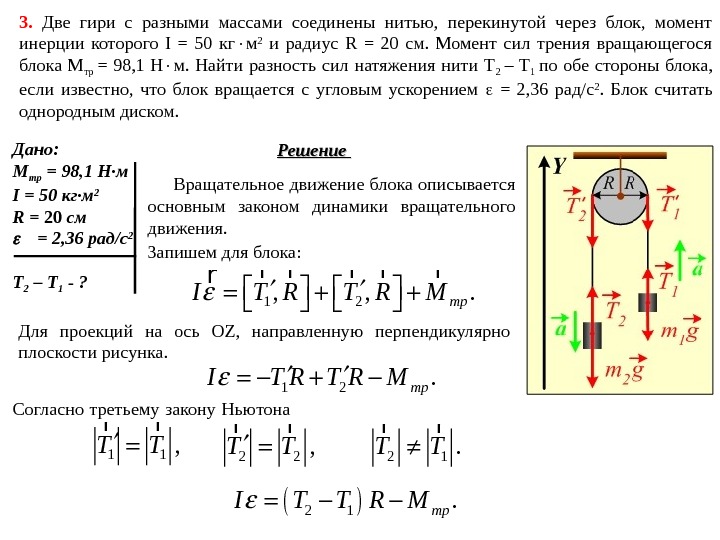
 3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что блок вращается с угловым ускорением = 2, 36 рад/c 2. Блок считать однородным диском. Дано: M тр = 98, 1 Н·м I = 50 кг·м 2 R = 20 cм = 2, 36 рад /c 2 Т 2 – Т 1 — ? Решение Вращательное движение блока описывается основным законом динамики вращательного движения. Запишем для блока: 1 2 , , . тр. I T R M r r rr Для проекций на ось OZ, направленную перпендикулярно плоскости рисунка. Согласно третьему закону Ньютона 1 1, T T r r 2 2, T T r r 2 1. T T r r 1 2. тр. I T R M 2 1. тр. I T T R M
3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что блок вращается с угловым ускорением = 2, 36 рад/c 2. Блок считать однородным диском. Дано: M тр = 98, 1 Н·м I = 50 кг·м 2 R = 20 cм = 2, 36 рад /c 2 Т 2 – Т 1 — ? Решение Вращательное движение блока описывается основным законом динамики вращательного движения. Запишем для блока: 1 2 , , . тр. I T R M r r rr Для проекций на ось OZ, направленную перпендикулярно плоскости рисунка. Согласно третьему закону Ньютона 1 1, T T r r 2 2, T T r r 2 1. T T r r 1 2. тр. I T R M 2 1. тр. I T T R M
 3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 1 – Т 2 по обе стороны блока, если известно, что блок вращается с угловым ускорением = 2, 36 рад/c 2. Блок считать однородным диском. Решение (продолжение) 2 1. тр. I T T R M Из этого уравнения получаем: 2 1. тр I M T T R 2 1 50 2, 34 98, 1 1080. 0, 2 T T H Ответ: T 2 – T 21 =1, 08 к. Н.
3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 1 – Т 2 по обе стороны блока, если известно, что блок вращается с угловым ускорением = 2, 36 рад/c 2. Блок считать однородным диском. Решение (продолжение) 2 1. тр. I T T R M Из этого уравнения получаем: 2 1. тр I M T T R 2 1 50 2, 34 98, 1 1080. 0, 2 T T H Ответ: T 2 – T 21 =1, 08 к. Н.
 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском. Дано: M тр = 98, 1 Н·м I = 50 кг·м 2 R = 20 cм m 1 = 1 кг m 2 = 1, 5 кг Т 2 – Т 1 — ? Решение Поступательное движение гирь описывается вторым законом Ньютона, а вращательное движение блока – основным законом динамики вращательного движения. Запишем для гирь и блока: 1 1. m a m g T rr r 2 1 2 2. m a m g T rr r 1 2 , , . тр. I T R M r r rr Перепишем систему уравнений. Для этого первое и второе уравнения запишем для проекций на вертикальную ось OY, а третье – для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.
3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском. Дано: M тр = 98, 1 Н·м I = 50 кг·м 2 R = 20 cм m 1 = 1 кг m 2 = 1, 5 кг Т 2 – Т 1 — ? Решение Поступательное движение гирь описывается вторым законом Ньютона, а вращательное движение блока – основным законом динамики вращательного движения. Запишем для гирь и блока: 1 1. m a m g T rr r 2 1 2 2. m a m g T rr r 1 2 , , . тр. I T R M r r rr Перепишем систему уравнений. Для этого первое и второе уравнения запишем для проекций на вертикальную ось OY, а третье – для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.
 Решение (продолжение) 1 1, m a m g T 2 1 2 2, m a m g T 1 2. тр. I T R M Согласно третьему закону Ньютона 1 1, T T r r 2 2, T T r r 2 1. T T r r Величину углового ускорения ε можно выразить через величину линейного ускорения a: . a R Нить нерастяжима, поэтому 2 1. a a a r r 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском.
Решение (продолжение) 1 1, m a m g T 2 1 2 2, m a m g T 1 2. тр. I T R M Согласно третьему закону Ньютона 1 1, T T r r 2 2, T T r r 2 1. T T r r Величину углового ускорения ε можно выразить через величину линейного ускорения a: . a R Нить нерастяжима, поэтому 2 1. a a a r r 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском.
 Решение (продолжение) 1 1 1, m a m g T 2 2 2, m a m g T 2 1. тр a I T R M R Система уравнений приобретает вид: Вычтем из второго уравнения первое и выполним элементарные преобразования в третьем: 1 2 2 1, m m a m m g T T 2 1. тр a I T T R M R 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском.
Решение (продолжение) 1 1 1, m a m g T 2 2 2, m a m g T 2 1. тр a I T R M R Система уравнений приобретает вид: Вычтем из второго уравнения первое и выполним элементарные преобразования в третьем: 1 2 2 1, m m a m m g T T 2 1. тр a I T T R M R 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском.
 Решение (продолжение) 1 2 2 1, m m a m m g T T 2 1. тр a I T T R M R 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском. Разделим первое уравнение на второе: 1 2 2 1 2 1 , тр m m R m m g T T I T T R M 1 2 2 1 2 1, трm m T T R M R I m m g T T 2 1 2 1, трm m T T R m m M R I m m g I T T
Решение (продолжение) 1 2 2 1, m m a m m g T T 2 1. тр a I T T R M R 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском. Разделим первое уравнение на второе: 1 2 2 1 2 1 , тр m m R m m g T T I T T R M 1 2 2 1 2 1, трm m T T R M R I m m g T T 2 1 2 1, трm m T T R m m M R I m m g I T T
 Решение (продолжение) 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском. 2 1 2 1, трm m T T R m m M R I m m g I T T 2 2 1 1 2 2 1, тр. T T I m m R m m M R Ig m m 1 2 2 12 1 2. трm m M R Ig m m T T I m m R 2 12 1 1, 5 98, 1 0, 2 50 9, 81 1, 5 1 5, 9. 50 1 1, 5 0, 2 T T H
Решение (продолжение) 3 А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кг м 2 и радиус R = 20 см. Момент сил трения вращающегося блока М тр = 98, 1 Н м. Найти разность сил натяжения нити Т 2 – Т 1 по обе стороны блока, если известно, что массы гирь m 1 = 1 кг, m 2 = 1, 5 кг. Блок считать однородным диском. 2 1 2 1, трm m T T R m m M R I m m g I T T 2 2 1 1 2 2 1, тр. T T I m m R m m M R Ig m m 1 2 2 12 1 2. трm m M R Ig m m T T I m m R 2 12 1 1, 5 98, 1 0, 2 50 9, 81 1, 5 1 5, 9. 50 1 1, 5 0, 2 T T H
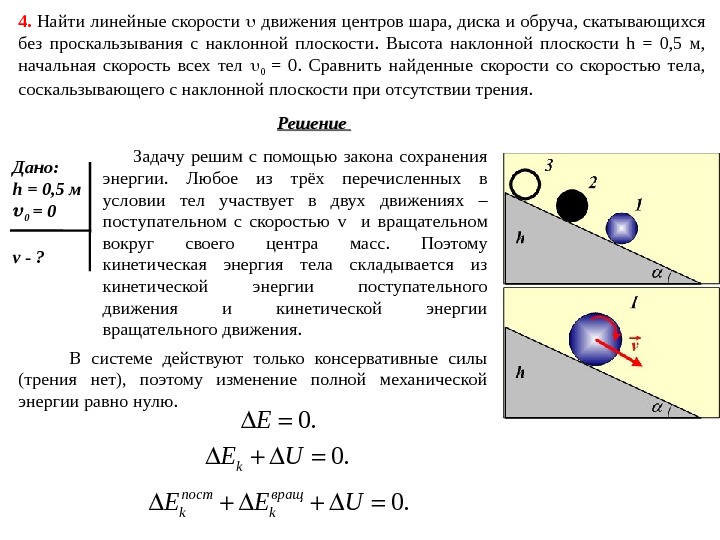
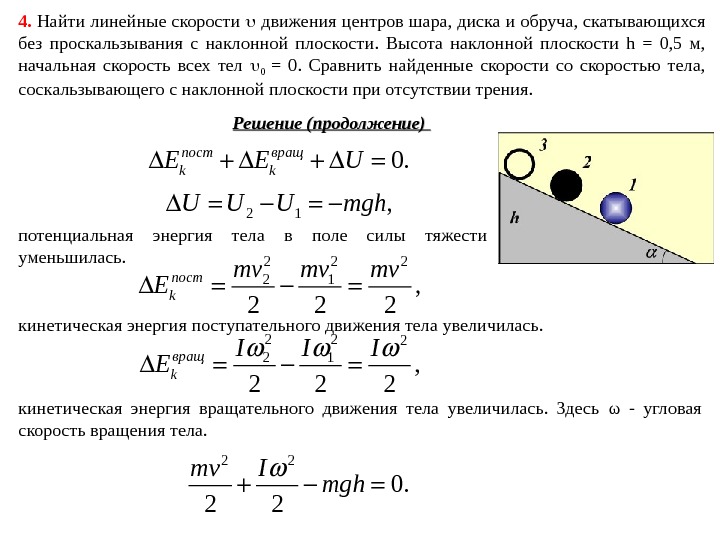
 4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение Дано: h = 0, 5 м 0 = 0 v — ? Задачу решим с помощью закона сохранения энергии. Любое из трёх перечисленных в условии тел участвует в двух движениях – поступательном с скоростью v и вращательном вокруг своего центра масс. Поэтому кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения. В системе действуют только консервативные силы (трения нет), поэтому изменение полной механической энергии равно нулю. 0. E 0. k. E U 0. пост вращ k k. E E U
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение Дано: h = 0, 5 м 0 = 0 v — ? Задачу решим с помощью закона сохранения энергии. Любое из трёх перечисленных в условии тел участвует в двух движениях – поступательном с скоростью v и вращательном вокруг своего центра масс. Поэтому кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения. В системе действуют только консервативные силы (трения нет), поэтому изменение полной механической энергии равно нулю. 0. E 0. k. E U 0. пост вращ k k. E E U
 4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение (продолжение) 0. пост вращ k k. E E U потенциальная энергия тела в поле силы тяжести уменьшилась. 2 1, U U U mgh 2 22 2 1, 2 2 2 пост k mv mvmv E кинетическая энергия поступательного движения тела увеличилась. 2 22 2 1, 2 2 2 вращ k I II E кинетическая энергия вращательного движения тела увеличилась. Здесь ω — угловая скорость вращения тела. 2 2 0. 2 2 mv I mgh
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение (продолжение) 0. пост вращ k k. E E U потенциальная энергия тела в поле силы тяжести уменьшилась. 2 1, U U U mgh 2 22 2 1, 2 2 2 пост k mv mvmv E кинетическая энергия поступательного движения тела увеличилась. 2 22 2 1, 2 2 2 вращ k I II E кинетическая энергия вращательного движения тела увеличилась. Здесь ω — угловая скорость вращения тела. 2 2 0. 2 2 mv I mgh
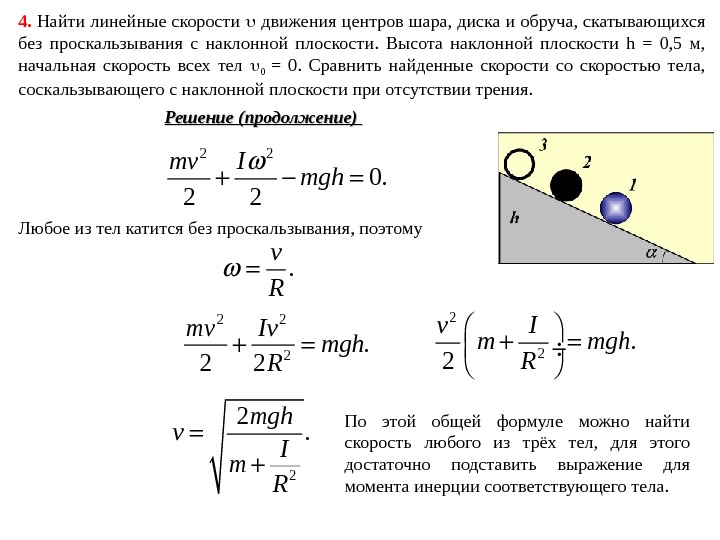
 4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение (продолжение) 2 2 0. 2 2 mv I mgh Любое из тел катится без проскальзывания, поэтому . v R 2 2 2 mv Iv mgh R 2 2. 2 v I m mgh R 2 2. mgh v I m R По этой общей формуле можно найти скорость любого из трёх тел, для этого достаточно подставить выражение для момента инерции соответствующего тела.
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение (продолжение) 2 2 0. 2 2 mv I mgh Любое из тел катится без проскальзывания, поэтому . v R 2 2 2 mv Iv mgh R 2 2. 2 v I m mgh R 2 2. mgh v I m R По этой общей формуле можно найти скорость любого из трёх тел, для этого достаточно подставить выражение для момента инерции соответствующего тела.
 4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение (продолжение) 2 2. mgh v I m R 2 1 2. 5 I m. R 1. Шар: 2 2 10 2, 65. 227 1 55 mgh ghм v gh m. Rс m R 2 1 1. 2 I m. R 2. Диск: 2 2 4 2, 56. 113 1 22 mgh ghм v gh m. Rс m R
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Решение (продолжение) 2 2. mgh v I m R 2 1 2. 5 I m. R 1. Шар: 2 2 10 2, 65. 227 1 55 mgh ghм v gh m. Rс m R 2 1 1. 2 I m. R 2. Диск: 2 2 4 2, 56. 113 1 22 mgh ghм v gh m. Rс m R
 4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Ответ: 1 = 2, 65 м/c, 2 = 2, 56 м/c, 3 = 2, 21 м/c; = 3, 13 м/c. Решение (продолжение) 2 1. I m. R 3. Обруч: 2 2 2, 21. 1 1 mgh ghм v gh m. Rс m R 4. Для тела, соскальзывающего без вращения по наклонной плоскости 2 0. 2 mv mgh 2 3, 13. м v gh с
4. Найти линейные скорости движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0, 5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Ответ: 1 = 2, 65 м/c, 2 = 2, 56 м/c, 3 = 2, 21 м/c; = 3, 13 м/c. Решение (продолжение) 2 1. I m. R 3. Обруч: 2 2 2, 21. 1 1 mgh ghм v gh m. Rс m R 4. Для тела, соскальзывающего без вращения по наклонной плоскости 2 0. 2 mv mgh 2 3, 13. м v gh с
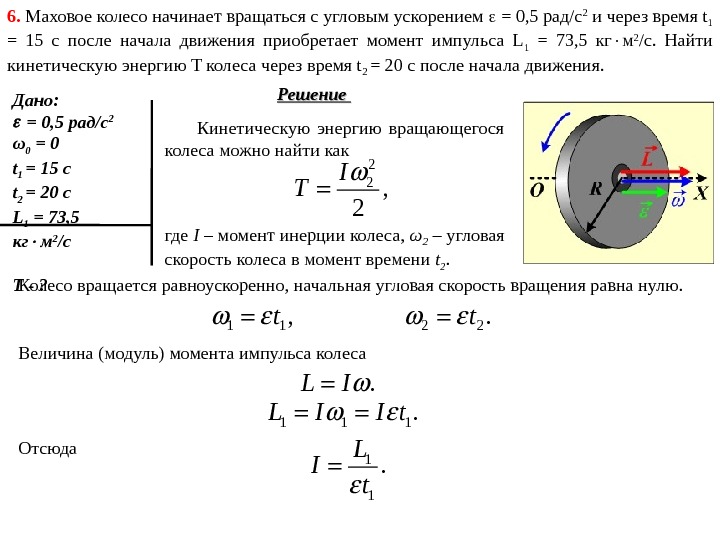
 6. Маховое колесо начинает вращаться с угловым ускорением = 0, 5 рад/c 2 и через время t 1 = 15 с после начала движения приобретает момент импульса L 1 = 73, 5 кг м 2 /c. Найти кинетическую энергию T колеса через время t 2 = 20 с после начала движения. Решение Дано: = 0, 5 рад/c 2 ω 0 = 0 t 1 = 15 с t 2 = 20 с L 1 = 73, 5 кг м 2 /c Т — ? Кинетическую энергию вращающегося колеса можно найти как 2 2, 2 I T где I – момент инерции колеса, ω 2 – угловая скорость колеса в момент времени t 2. Колесо вращается равноускоренно, начальная угловая скорость вращения равна нулю. 1 1, t 2 2. t Величина (модуль) момента импульса колеса. L I 1 1 1. L I I t Отсюда 1 1. L I t
6. Маховое колесо начинает вращаться с угловым ускорением = 0, 5 рад/c 2 и через время t 1 = 15 с после начала движения приобретает момент импульса L 1 = 73, 5 кг м 2 /c. Найти кинетическую энергию T колеса через время t 2 = 20 с после начала движения. Решение Дано: = 0, 5 рад/c 2 ω 0 = 0 t 1 = 15 с t 2 = 20 с L 1 = 73, 5 кг м 2 /c Т — ? Кинетическую энергию вращающегося колеса можно найти как 2 2, 2 I T где I – момент инерции колеса, ω 2 – угловая скорость колеса в момент времени t 2. Колесо вращается равноускоренно, начальная угловая скорость вращения равна нулю. 1 1, t 2 2. t Величина (модуль) момента импульса колеса. L I 1 1 1. L I I t Отсюда 1 1. L I t
 6. Маховое колесо начинает вращаться с угловым ускорением = 0, 5 рад/c 2 и через время t 1 = 15 с после начала движения приобретает момент импульса L 1 = 73, 5 кг м 2 /c. Найти кинетическую энергию T колеса через время t 2 = 20 с после начала движения. Ответ: T=490 Дж. Решение (продолжение) 2 2, 2 I T 2 2, t 1 1. L I t Подставим в формулу для кинетической энергии полученные выражения для момента инерции и угловой скорости. 2 2 2 12 2 I L T t 2 2 12 L t t 2 1. 2 L t t 22 1 73, 5 0, 5 20 490. 2 2 15 L t TДж t
6. Маховое колесо начинает вращаться с угловым ускорением = 0, 5 рад/c 2 и через время t 1 = 15 с после начала движения приобретает момент импульса L 1 = 73, 5 кг м 2 /c. Найти кинетическую энергию T колеса через время t 2 = 20 с после начала движения. Ответ: T=490 Дж. Решение (продолжение) 2 2, 2 I T 2 2, t 1 1. L I t Подставим в формулу для кинетической энергии полученные выражения для момента инерции и угловой скорости. 2 2 2 12 2 I L T t 2 2 12 L t t 2 1. 2 L t t 22 1 73, 5 0, 5 20 490. 2 2 15 L t TДж t
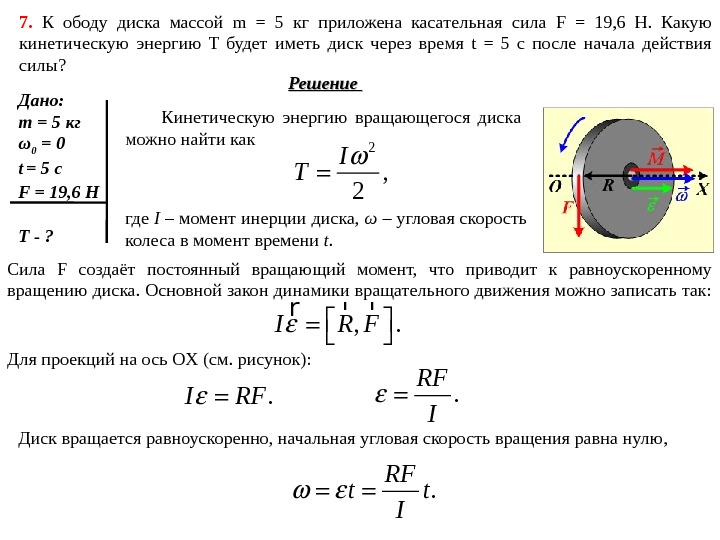
 7. К ободу диска массой m = 5 кг приложена касательная сила F = 19, 6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы? Решение Дано: m = 5 кг ω 0 = 0 t = 5 с F = 19, 6 Н Т — ? Кинетическую энергию вращающегося диска можно найти как 2 , 2 I T где I – момент инерции диска, ω – угловая скорость колеса в момент времени t. Сила F создаёт постоянный вращающий момент, что приводит к равноускоренному вращению диска. Основной закон динамики вращательного движения можно записать так: , . I R F r rr Для проекций на ось OX ( см. рисунок): . I RF. RF I Диск вращается равноускоренно, начальная угловая скорость вращения равна нулю, . RF t t I
7. К ободу диска массой m = 5 кг приложена касательная сила F = 19, 6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы? Решение Дано: m = 5 кг ω 0 = 0 t = 5 с F = 19, 6 Н Т — ? Кинетическую энергию вращающегося диска можно найти как 2 , 2 I T где I – момент инерции диска, ω – угловая скорость колеса в момент времени t. Сила F создаёт постоянный вращающий момент, что приводит к равноускоренному вращению диска. Основной закон динамики вращательного движения можно записать так: , . I R F r rr Для проекций на ось OX ( см. рисунок): . I RF. RF I Диск вращается равноускоренно, начальная угловая скорость вращения равна нулю, . RF t t I
 7. К ободу диска массой m = 5 кг приложена касательная сила F = 19, 6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы? Ответ: T=1, 92 к. Дж. Решение (продолжение) 2 , 2 I T . RF t t I 22 2 2 I I RF T t I 2 2 2. 2 R F t I Момент инерции диска относительно данной оси вращения 2. 2 m. R I 2 2 R F T t I 2 2 2 R F t m. R 2 2. F t m 2 2 19, 6 5 1920. 5 F t TДж m
7. К ободу диска массой m = 5 кг приложена касательная сила F = 19, 6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы? Ответ: T=1, 92 к. Дж. Решение (продолжение) 2 , 2 I T . RF t t I 22 2 2 I I RF T t I 2 2 2. 2 R F t I Момент инерции диска относительно данной оси вращения 2. 2 m. R I 2 2 R F T t I 2 2 2 R F t m. R 2 2. F t m 2 2 19, 6 5 1920. 5 F t TДж m
 8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? Дано: l = 8 5 см v — ? Решение Если мы сообщим нижнему концу стержня некоторую скорость, он сможет совершить полный оборот вокруг оси, проходящей через точку О. Если эта скорость минимальная из всех возможных, при которых стержень совершит оборот, то в верхней точке скорость стержня будет очень близка к нулю (рис. 2). Для определения минимальной скорости, при которой возможен полный оборот стержня применим закон сохранения энергии. Трение в системе отсутствует, поэтому можно считать, что все силы, действующие в системе консервативны. 0. вращ k. E U 0. E Изменение потенциальной энергии в поле сил тяжести определим по изменению положения центра тяжести стержня, который совпадает с его геометрическим центром. . U mgh mgl
8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? Дано: l = 8 5 см v — ? Решение Если мы сообщим нижнему концу стержня некоторую скорость, он сможет совершить полный оборот вокруг оси, проходящей через точку О. Если эта скорость минимальная из всех возможных, при которых стержень совершит оборот, то в верхней точке скорость стержня будет очень близка к нулю (рис. 2). Для определения минимальной скорости, при которой возможен полный оборот стержня применим закон сохранения энергии. Трение в системе отсутствует, поэтому можно считать, что все силы, действующие в системе консервативны. 0. вращ k. E U 0. E Изменение потенциальной энергии в поле сил тяжести определим по изменению положения центра тяжести стержня, который совпадает с его геометрическим центром. . U mgh mgl
 8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? . U mgh mgl Решение (продолжение) Потенциальная энергия стержня в поле сил тяжести увеличилась. Кинетическая энергия стержня уменьшилась, так как в верхней точке он практически остановился. 2 2 0. 2 2 k I I E Здесь ω — начальная угловая скорость стержня. . v v R l 2 2 2 k I Iv E l Момент инерции стержня относительно точки O 2. 3 ml I 2 2 2 3 2 k Iv ml v E l l 2. 6 mv
8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? . U mgh mgl Решение (продолжение) Потенциальная энергия стержня в поле сил тяжести увеличилась. Кинетическая энергия стержня уменьшилась, так как в верхней точке он практически остановился. 2 2 0. 2 2 k I I E Здесь ω — начальная угловая скорость стержня. . v v R l 2 2 2 k I Iv E l Момент инерции стержня относительно точки O 2. 3 ml I 2 2 2 3 2 k Iv ml v E l l 2. 6 mv
 8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? Ответ: =7, 1 м/c. 0, вращ k. E U Решение (продолжение) , U mgl 2. 6 k mv E 2 0. 6 mv mgl 2. 6 mv mgl 6. v gl 6 6 9, 8 0, 85 7, 1. м v gl с
8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? Ответ: =7, 1 м/c. 0, вращ k. E U Решение (продолжение) , U mgl 2. 6 k mv E 2 0. 6 mv mgl 2. 6 mv mgl 6. v gl 6 6 9, 8 0, 85 7, 1. м v gl с
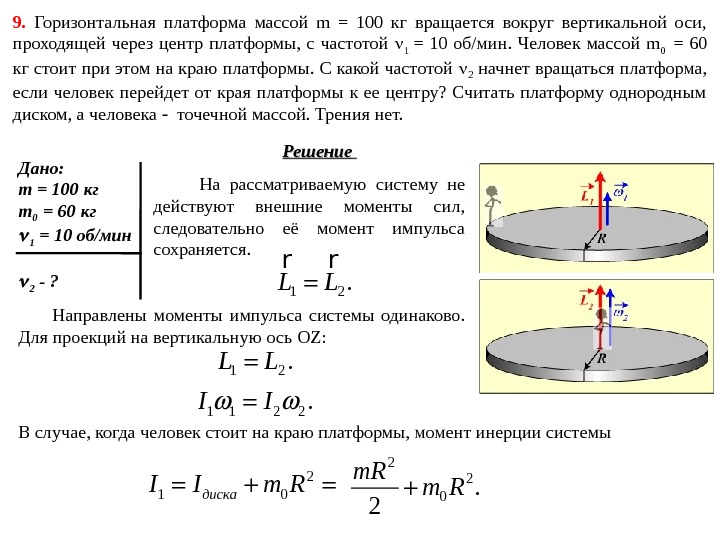
 9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет. Решение Дано: m = 100 кг m 0 = 60 кг 1 = 10 об/мин 2 — ? На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется. 1 2. L L r r Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ: 1 2. L L 1 1 2 2. I I В случае, когда человек стоит на краю платформы, момент инерции системы 2 1 0 диска. I I m R 2 2 0. 2 m. R m R
9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет. Решение Дано: m = 100 кг m 0 = 60 кг 1 = 10 об/мин 2 — ? На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется. 1 2. L L r r Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ: 1 2. L L 1 1 2 2. I I В случае, когда человек стоит на краю платформы, момент инерции системы 2 1 0 диска. I I m R 2 2 0. 2 m. R m R
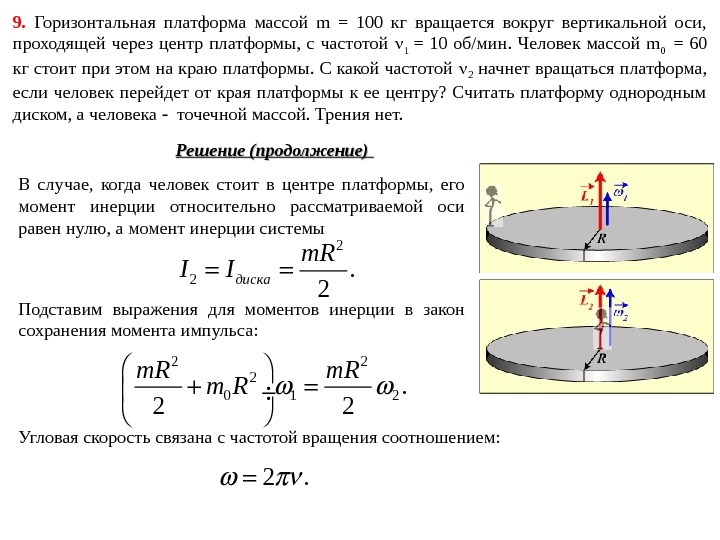
 9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет. В случае, когда человек стоит в центре платформы, его момент инерции относительно рассматриваемой оси равен нулю, а момент инерции системы Решение (продолжение) 2 2. 2 диска m. R I I Подставим выражения для моментов инерции в закон сохранения момента импульса: 2 2 2 0 1 2. 2 2 m. R m R Угловая скорость связана с частотой вращения соотношением: 2.
9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет. В случае, когда человек стоит в центре платформы, его момент инерции относительно рассматриваемой оси равен нулю, а момент инерции системы Решение (продолжение) 2 2. 2 диска m. R I I Подставим выражения для моментов инерции в закон сохранения момента импульса: 2 2 2 0 1 2. 2 2 m. R m R Угловая скорость связана с частотой вращения соотношением: 2.
 9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет. Ответ: 2 = 22 об/мин. 2 2 2 0 1 2, 2 2 m. R m R 2. Решение (продолжение) 2 2 2 0 1 22 2 , 2 2 m. R m R 2 2 2 0 1 22 , m. R 0 1 22 , m m m 0 2 1 2100 2 60 10 22. 100 m mоб mмин
9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m 0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека точечной массой. Трения нет. Ответ: 2 = 22 об/мин. 2 2 2 0 1 2, 2 2 m. R m R 2. Решение (продолжение) 2 2 2 0 1 22 2 , 2 2 m. R m R 2 2 2 0 1 22 , m. R 0 1 22 , m m m 0 2 1 2100 2 60 10 22. 100 m mоб mмин
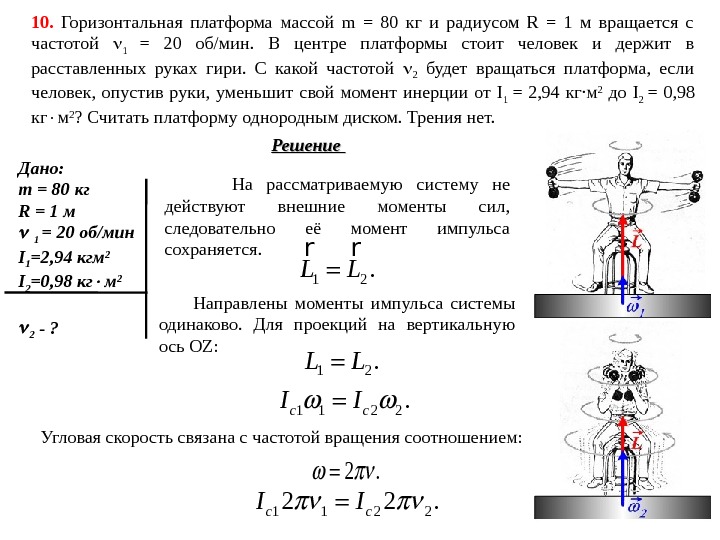
 10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I 1 = 2, 94 кг·м 2 до I 2 = 0, 98 кг м 2 ? Считать платформу однородным диском. Трения нет. Решение Дано: m = 80 кг R = 1 м 1 = 20 об/мин I 1 =2, 94 кгм 2 I 2 =0, 98 кг м 2 2 — ? На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется. 1 2. L L r r Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ: 1 2. L L 1 1 2 2. c c. I I Угловая скорость связана с частотой вращения соотношением: 2. 1 1 2 22 2. c c. I I
10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I 1 = 2, 94 кг·м 2 до I 2 = 0, 98 кг м 2 ? Считать платформу однородным диском. Трения нет. Решение Дано: m = 80 кг R = 1 м 1 = 20 об/мин I 1 =2, 94 кгм 2 I 2 =0, 98 кг м 2 2 — ? На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется. 1 2. L L r r Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ: 1 2. L L 1 1 2 2. c c. I I Угловая скорость связана с частотой вращения соотношением: 2. 1 1 2 22 2. c c. I I
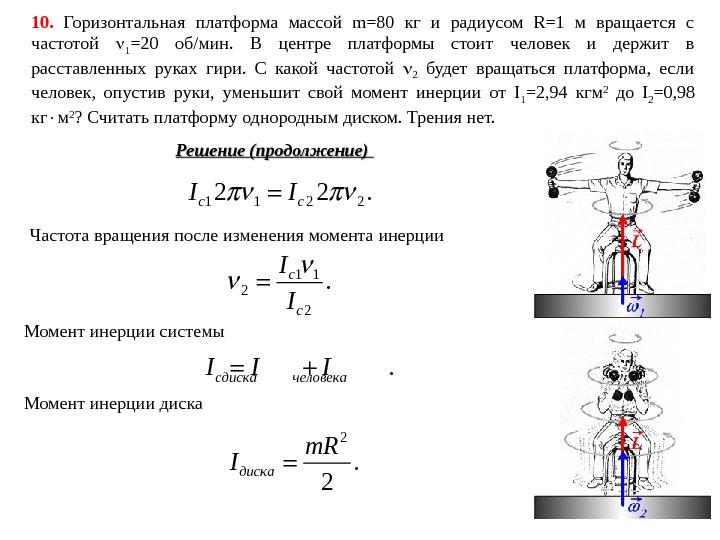
 10. Горизонтальная платформа массой m=80 кг и радиусом R=1 м вращается с частотой 1 =20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I 1 =2, 94 кгм 2 до I 2 =0, 98 кг м 2 ? Считать платформу однородным диском. Трения нет. Решение (продолжение) 1 1 2 22 2. c c. I I Частота вращения после изменения момента инерции 1 1 2 2. c c I I Момент инерции системы . cдиска человека. I I I 2. 2 диска m. R I Момент инерции диска
10. Горизонтальная платформа массой m=80 кг и радиусом R=1 м вращается с частотой 1 =20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I 1 =2, 94 кгм 2 до I 2 =0, 98 кг м 2 ? Считать платформу однородным диском. Трения нет. Решение (продолжение) 1 1 2 22 2. c c. I I Частота вращения после изменения момента инерции 1 1 2 2. c c I I Момент инерции системы . cдиска человека. I I I 2. 2 диска m. R I Момент инерции диска
 10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I 1 = 2, 94 кг·м 2 до I 2 = 0, 98 кг м 2 ? Считать платформу однородным диском. Трения нет. Ответ: 2 =21 об/мин. Решение (продолжение) , cдиска человека. I I I 2. 2 диска m. R I 2 1 1, 2 c m. R I I 2 2 2. 2 c m. R I I 2 1 1 1 2 12 2 2 c c m. R I I m. RI I 2 1 12 2 2. 2 m. R I 2 12 2 280 1 2 2, 94 20 21. 2 80 1 2 0, 98 m. R Iоб m. R Iмин
10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I 1 = 2, 94 кг·м 2 до I 2 = 0, 98 кг м 2 ? Считать платформу однородным диском. Трения нет. Ответ: 2 =21 об/мин. Решение (продолжение) , cдиска человека. I I I 2. 2 диска m. R I 2 1 1, 2 c m. R I I 2 2 2. 2 c m. R I I 2 1 1 1 2 12 2 2 c c m. R I I m. RI I 2 1 12 2 2. 2 m. R I 2 12 2 280 1 2 2, 94 20 21. 2 80 1 2 0, 98 m. R Iоб m. R Iмин
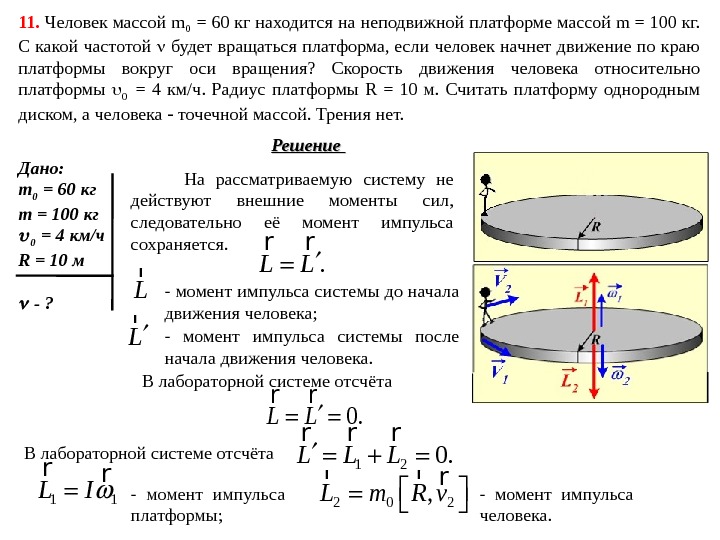
 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет. Решение Дано: m 0 = 60 кг m = 100 кг 0 = 4 км/ч R = 10 м — ? На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется. . L L r r В лабораторной системе отсчёта 0. L L r r — момент импульса системы до начала движения человека; L r — момент импульса системы после начала движения человека. В лабораторной системе отсчёта 1 20. L L L r r r 1 1 L I rr — момент импульса платформы; 2 0 2, L m R v r rr — момент импульса человека.
11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет. Решение Дано: m 0 = 60 кг m = 100 кг 0 = 4 км/ч R = 10 м — ? На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется. . L L r r В лабораторной системе отсчёта 0. L L r r — момент импульса системы до начала движения человека; L r — момент импульса системы после начала движения человека. В лабораторной системе отсчёта 1 20. L L L r r r 1 1 L I rr — момент импульса платформы; 2 0 2, L m R v r rr — момент импульса человека.
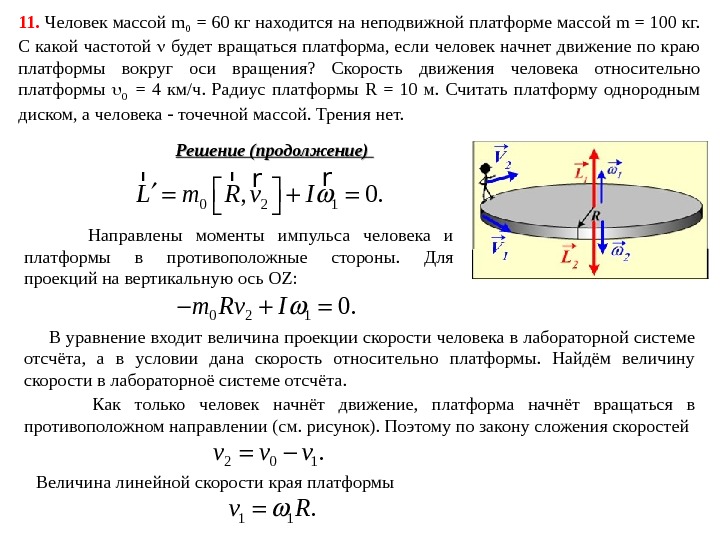
 Решение (продолжение) 0 2 1, 0. L m R v I r rrr Направлены моменты импульса человека и платформы в противоположные стороны. Для проекций на вертикальную ось OZ: 0 2 10. m Rv I В уравнение входит величина проекции скорости человека в лабораторной системе отсчёта, а в условии дана скорость относительно платформы. Найдём величину скорости в лабораторноё системе отсчёта. Как только человек начнёт движение, платформа начнёт вращаться в противоположном направлении (см. рисунок). Поэтому по закону сложения скоростей 2 0 1. v v v Величина линейной скорости края платформы 1 1. v R 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
Решение (продолжение) 0 2 1, 0. L m R v I r rrr Направлены моменты импульса человека и платформы в противоположные стороны. Для проекций на вертикальную ось OZ: 0 2 10. m Rv I В уравнение входит величина проекции скорости человека в лабораторной системе отсчёта, а в условии дана скорость относительно платформы. Найдём величину скорости в лабораторноё системе отсчёта. Как только человек начнёт движение, платформа начнёт вращаться в противоположном направлении (см. рисунок). Поэтому по закону сложения скоростей 2 0 1. v v v Величина линейной скорости края платформы 1 1. v R 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
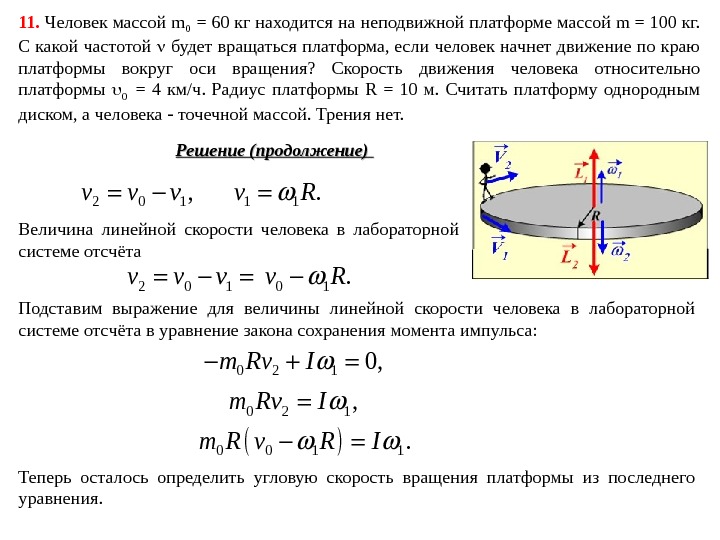
 Решение (продолжение) 2 0 1, v v v 1 1. v R 2 0 1 v v v Величина линейной скорости человека в лабораторной системе отсчёта 0 1. v R Подставим выражение для величины линейной скорости человека в лабораторной системе отсчёта в уравнение закона сохранения момента импульса: 0 2 10, m Rv I 0 2 1, m Rv I 0 0 1 1. m R v R I Теперь осталось определить угловую скорость вращения платформы из последнего уравнения. 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
Решение (продолжение) 2 0 1, v v v 1 1. v R 2 0 1 v v v Величина линейной скорости человека в лабораторной системе отсчёта 0 1. v R Подставим выражение для величины линейной скорости человека в лабораторной системе отсчёта в уравнение закона сохранения момента импульса: 0 2 10, m Rv I 0 2 1, m Rv I 0 0 1 1. m R v R I Теперь осталось определить угловую скорость вращения платформы из последнего уравнения. 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
 Решение (продолжение) 0 0 1 1, m R v R I 2 0 0 0 1 1, m Rv m R I 0 0 12 0. m Rv m R I Напомним, что I – момент инерции платформы, которая имеет форму диска. 21. 2 I m. R 0 0 1 2 2 0 1 2 m Rv m R m. R 0 0 0 2. 2 m v m R m. R 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
Решение (продолжение) 0 0 1 1, m R v R I 2 0 0 0 1 1, m Rv m R I 0 0 12 0. m Rv m R I Напомним, что I – момент инерции платформы, которая имеет форму диска. 21. 2 I m. R 0 0 1 2 2 0 1 2 m Rv m R m. R 0 0 0 2. 2 m v m R m. R 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
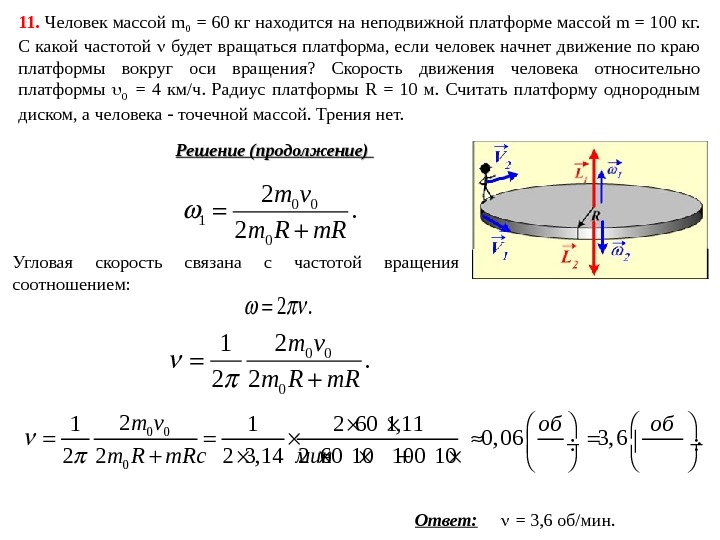
 Ответ: = 3, 6 об/мин. 0 0 1 0 2. 2 m v m R m. R Решение (продолжение) Угловая скорость связана с частотой вращения соотношением: 2. 0 0 0 21. 2 2 m v m R m. R 0 0 0 21 1 2 60 1, 11 0, 06 3, 6. 2 2 2 3, 14 2 60 10 10 m vоб об m R m. Rс мин 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
Ответ: = 3, 6 об/мин. 0 0 1 0 2. 2 m v m R m. R Решение (продолжение) Угловая скорость связана с частотой вращения соотношением: 2. 0 0 0 21. 2 2 m v m R m. R 0 0 0 21 1 2 60 1, 11 0, 06 3, 6. 2 2 2 3, 14 2 60 10 10 m vоб об m R m. Rс мин 11. Человек массой m 0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека точечной массой. Трения нет.
