Презентация Лекция 3 Работа Энергия full





































- Размер: 2.5 Mегабайта
- Количество слайдов: 47
Описание презентации Презентация Лекция 3 Работа Энергия full по слайдам
 Работа. Энергия. Применение законов сохранения.
Работа. Энергия. Применение законов сохранения.












 А 1. Найти работу A , которую нужно совершить, чтобы увеличить скорость движения тела массой m = 1 т от 1 = 2 м/с до 2 = 6 м/с на пути S = 10 м. На всем пути действует сила трения F тр = 2 Н. Дано: m =1000 кг u 1 = 2 м /c u 2 = 2 м /c F = 2 H А = ? Решение Согласно определению, работа 2 2 1 1 cos. s s. A Fds F ds r r F – сила, s – перемещение, α – угол между векторами силы и перемещения. Выберем направление оси OX так, чтобы оно совпадало с направлением скорости тела (см. рис. ). Скорость возрастает, следовательно, ускорение направлено вправо, а силы – так как показано на рисунке. Запишем второй закон Ньютона в проекции на ось OX. . трma F F Отсюда. тр. F ma F Величину ускорения найдем из кинематического уравнения: 2 2 2 1. 2 V V a S
А 1. Найти работу A , которую нужно совершить, чтобы увеличить скорость движения тела массой m = 1 т от 1 = 2 м/с до 2 = 6 м/с на пути S = 10 м. На всем пути действует сила трения F тр = 2 Н. Дано: m =1000 кг u 1 = 2 м /c u 2 = 2 м /c F = 2 H А = ? Решение Согласно определению, работа 2 2 1 1 cos. s s. A Fds F ds r r F – сила, s – перемещение, α – угол между векторами силы и перемещения. Выберем направление оси OX так, чтобы оно совпадало с направлением скорости тела (см. рис. ). Скорость возрастает, следовательно, ускорение направлено вправо, а силы – так как показано на рисунке. Запишем второй закон Ньютона в проекции на ось OX. . трma F F Отсюда. тр. F ma F Величину ускорения найдем из кинематического уравнения: 2 2 2 1. 2 V V a S
 А 1. Найти работу A , которую нужно совершить, чтобы увеличить скорость движения тела массой m = 1 кг от 1 = 2 м/с до 2 = 6 м/с на пути S = 10 м. На всем пути действует сила трения F тр = 2 Н. Ответ: A = 36 Дж. Решение (продолжение) Сила, действующая на тело, постоянна. Угол между векторами силы и перемещения равен нулю, cos 0 = 1. . тр. F ma F 2 2 2 1. 2 V V a S 2 2 2 1. 2 тр V V F m F S 2 1 coss s. A F ds F S 2 2 2 1 2 тр V V m F S S 2 2 2 1. 2 тр. V V m F S 36 4 2 10 36. 2 AДж
А 1. Найти работу A , которую нужно совершить, чтобы увеличить скорость движения тела массой m = 1 кг от 1 = 2 м/с до 2 = 6 м/с на пути S = 10 м. На всем пути действует сила трения F тр = 2 Н. Ответ: A = 36 Дж. Решение (продолжение) Сила, действующая на тело, постоянна. Угол между векторами силы и перемещения равен нулю, cos 0 = 1. . тр. F ma F 2 2 2 1. 2 V V a S 2 2 2 1. 2 тр V V F m F S 2 1 coss s. A F ds F S 2 2 2 1 2 тр V V m F S S 2 2 2 1. 2 тр. V V m F S 36 4 2 10 36. 2 AДж
 А 2. Камень падает с некоторой высоты без начальной скорости в течение времени t = 1, 43 с. Найти кинетическую энергию камня E k и изменение его потенциальной энергии Δ U к тому моменту, когда камень достигнет средней точки пути. Масса камня m = 2 кг. Дано: t = 1, 43 c m = 2 кг E k = ? U = ? Решение 1. Выберем начало отсчёта потенциальной энергии в точке падения камня (см. рисунок). 2. Если пренебречь силой сопротивления воздуха, то в системе действует только сила тяжести, которая является потенциальной. Следовательно, изменение полной механической энергии равно нулю (полная механическая энергия сохраняется)0. E 0. k. E E U U — потенциальная энергия тела в однородном поле силы тяжести. 1 0. 2 2 H H U U U mg mg. H mg
А 2. Камень падает с некоторой высоты без начальной скорости в течение времени t = 1, 43 с. Найти кинетическую энергию камня E k и изменение его потенциальной энергии Δ U к тому моменту, когда камень достигнет средней точки пути. Масса камня m = 2 кг. Дано: t = 1, 43 c m = 2 кг E k = ? U = ? Решение 1. Выберем начало отсчёта потенциальной энергии в точке падения камня (см. рисунок). 2. Если пренебречь силой сопротивления воздуха, то в системе действует только сила тяжести, которая является потенциальной. Следовательно, изменение полной механической энергии равно нулю (полная механическая энергия сохраняется)0. E 0. k. E E U U — потенциальная энергия тела в однородном поле силы тяжести. 1 0. 2 2 H H U U U mg mg. H mg
 А 2. Камень падает с некоторой высоты без начальной скорости в течение времени t = 1, 43 с. Найти кинетическую энергию камня E k и изменение его потенциальной энергии Δ U к тому моменту, когда камень достигнет средней точки пути. Масса камня m = 2 кг. Ответ: E k = 98 Дж, Δ U = — 98 Дж. Решение (продолжение) Высоту, с которой падает тело найдём из кинематического уравнения движения: 2 ( ) 0, 2 gt y t H 2 22 9, 8 1, 43 98. 2 4 4 H mg t U mg. Дж 2. 2 gt H 0. k. E E U . k. E U В верхней точке тело покоится, следовательно в этой точке E k = 0. Поэтому 1 0 198. k k. E E UДж
А 2. Камень падает с некоторой высоты без начальной скорости в течение времени t = 1, 43 с. Найти кинетическую энергию камня E k и изменение его потенциальной энергии Δ U к тому моменту, когда камень достигнет средней точки пути. Масса камня m = 2 кг. Ответ: E k = 98 Дж, Δ U = — 98 Дж. Решение (продолжение) Высоту, с которой падает тело найдём из кинематического уравнения движения: 2 ( ) 0, 2 gt y t H 2 22 9, 8 1, 43 98. 2 4 4 H mg t U mg. Дж 2. 2 gt H 0. k. E E U . k. E U В верхней точке тело покоится, следовательно в этой точке E k = 0. Поэтому 1 0 198. k k. E E UДж
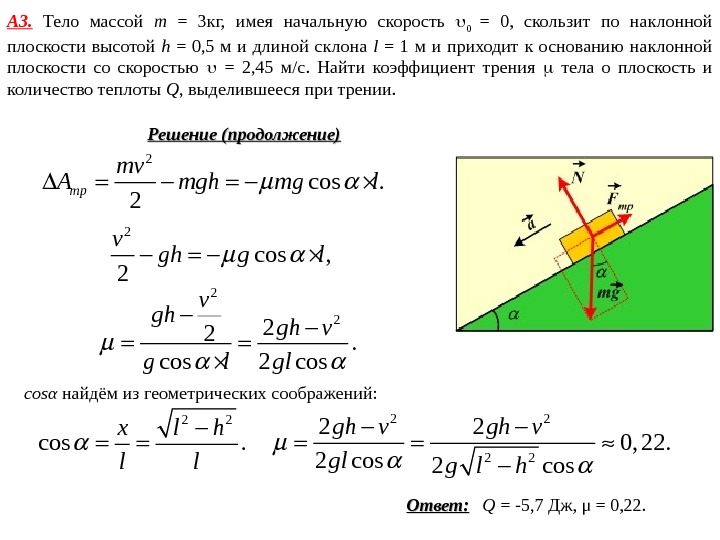
 Решение. А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. Дано: m = 3 кг 0 = 0 h = 0, 5 м l = 1 м = 2, 45 м/c — ? Q — ? Если пренебречь силой сопротивления воздуха, то в системе действуют сила тяжести и сила упругости, которые являются консервативными и неконсервативная сила трения. Поэтому изменение полной энергии тела равно работе неконсервативной силы. . kтр. E E U A Тело движется в однородном поле силы тяжести, высота над землёй уменьшается, поэтому. U mgh Скорость движения тела возрастает от нуля до v , поэтому 22 2 0. 2 2 2 k mvmv mv
Решение. А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. Дано: m = 3 кг 0 = 0 h = 0, 5 м l = 1 м = 2, 45 м/c — ? Q — ? Если пренебречь силой сопротивления воздуха, то в системе действуют сила тяжести и сила упругости, которые являются консервативными и неконсервативная сила трения. Поэтому изменение полной энергии тела равно работе неконсервативной силы. . kтр. E E U A Тело движется в однородном поле силы тяжести, высота над землёй уменьшается, поэтому. U mgh Скорость движения тела возрастает от нуля до v , поэтому 22 2 0. 2 2 2 k mvmv mv
 Решение ( ( продолжение ))А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. . kтр. E U A 2. 2 тр k mv A E U mgh Если считать, что количество выделившейся теплоты равно работе силы трения, то 2 2 3 2, 45 3 9, 8 0, 5 5, 7. 2 2 mv Q mgh. Дж Знак «-» указывает на то, что энергия в виде тепла выделилась, «ушла» из системы.
Решение ( ( продолжение ))А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. . kтр. E U A 2. 2 тр k mv A E U mgh Если считать, что количество выделившейся теплоты равно работе силы трения, то 2 2 3 2, 45 3 9, 8 0, 5 5, 7. 2 2 mv Q mgh. Дж Знак «-» указывает на то, что энергия в виде тепла выделилась, «ушла» из системы.
 Решение (продолжение)А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. Чтобы определить величину коэффициента трения, найдём работу силы трения, пользуясь определением работы. 2 2 1 1 cos. s s. A Fds F ds r r F – сила, s – перемещение, φ – угол между векторами силы и перемещения. Чтобы найти силу трения, запишем второй закон Ньютона: трma N mg F r r Величина силы трения скольжения F тр = μ N. В проекциях на оси координат (см. рисунок): sin , xma mg N 0 cos. mg N
Решение (продолжение)А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. Чтобы определить величину коэффициента трения, найдём работу силы трения, пользуясь определением работы. 2 2 1 1 cos. s s. A Fds F ds r r F – сила, s – перемещение, φ – угол между векторами силы и перемещения. Чтобы найти силу трения, запишем второй закон Ньютона: трma N mg F r r Величина силы трения скольжения F тр = μ N. В проекциях на оси координат (см. рисунок): sin , xma mg N 0 cos. mg N
 Решение ( ( продолжение)А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. sin , xma mg N 0 cos. mg N Из второго уравнения системы: cos. N mg Величина силы трения cos. тр. F N mg 2 1 cos. s тр s. A F ds F l Работа силы трения Угол между векторами силы трения и перемещения φ = 18 , 00 cos 1800 = — 1. cos. тр. A F l mg l
Решение ( ( продолжение)А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. sin , xma mg N 0 cos. mg N Из второго уравнения системы: cos. N mg Величина силы трения cos. тр. F N mg 2 1 cos. s тр s. A F ds F l Работа силы трения Угол между векторами силы трения и перемещения φ = 18 , 00 cos 1800 = — 1. cos. тр. A F l mg l
 Решение ( ( продолжение)А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. 2 cos. 2 тр mv A mgh mg l 2 cos , 2 v gh g l 2 2 22. cos 2 cos v gh gh v g l gl cos α найдём из геометрических соображений: 2 2 cos. x l h l l 2 2 2 0, 22. 2 cos gh v glg l h Ответ: Q = -5, 7 Дж, μ = 0, 22.
Решение ( ( продолжение)А 3. Тело массой m = 3 кг, имея начальную скорость 0 = 0, скользит по наклонной плоскости высотой h = 0, 5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью = 2, 45 м/c. Найти коэффициент трения тела о плоскость и количество теплоты Q , выделившееся при трении. 2 cos. 2 тр mv A mgh mg l 2 cos , 2 v gh g l 2 2 22. cos 2 cos v gh gh v g l gl cos α найдём из геометрических соображений: 2 2 cos. x l h l l 2 2 2 0, 22. 2 cos gh v glg l h Ответ: Q = -5, 7 Дж, μ = 0, 22.
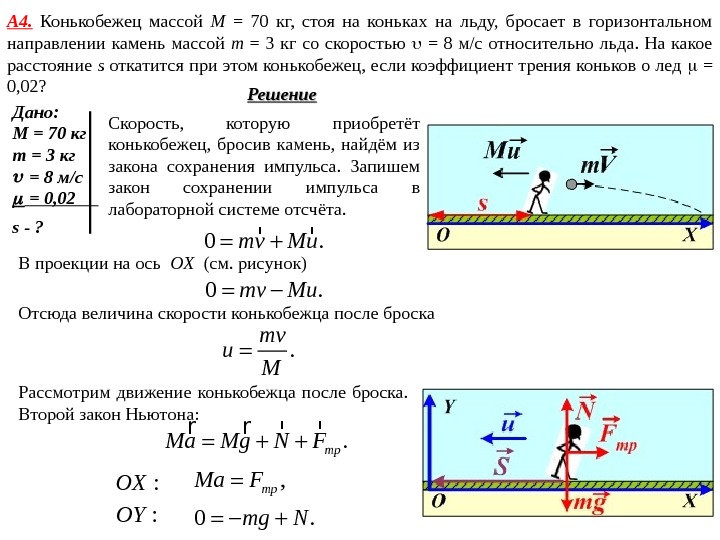
 Решение. А 4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с относительно льда. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0, 02? Дано: M = 70 кг m = 3 кг = 8 м/с = 0, 02 s — ? Скорость, которую приобретёт конькобежец, бросив камень, найдём из закона сохранения импульса. Запишем закон сохранении импульса в лабораторной системе отсчёта. 0. mv Mu r r В проекции на ось OX ( см. рисунок) 0. mv Mu Отсюда величина скорости конькобежца после броска . mv u M Рассмотрим движение конькобежца после броска. Второй закон Ньютона: . тр. Ma Mg N F r r , тр. Ma F 0. mg N : OX : OY
Решение. А 4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с относительно льда. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0, 02? Дано: M = 70 кг m = 3 кг = 8 м/с = 0, 02 s — ? Скорость, которую приобретёт конькобежец, бросив камень, найдём из закона сохранения импульса. Запишем закон сохранении импульса в лабораторной системе отсчёта. 0. mv Mu r r В проекции на ось OX ( см. рисунок) 0. mv Mu Отсюда величина скорости конькобежца после броска . mv u M Рассмотрим движение конькобежца после броска. Второй закон Ньютона: . тр. Ma Mg N F r r , тр. Ma F 0. mg N : OX : OY
 Решение (продолжение)А 4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0, 02? , трma F 0. Mg N : OX : OY Величина силы трения скольжения . тр. F N , N Mg. тр. F Mg Изменение полной механической энергии конькобежца равно работе неконсервативных сил, то есть работе силы трения. , тр. E A , k. E E U 0, U. kтр. E A 2 2 2 1 2 2 k Mv Mv E 2 2 0. 2 2 Mu Mu cos , тр тр. A F S , cos. тр тр. A F S Mg. S
Решение (продолжение)А 4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0, 02? , трma F 0. Mg N : OX : OY Величина силы трения скольжения . тр. F N , N Mg. тр. F Mg Изменение полной механической энергии конькобежца равно работе неконсервативных сил, то есть работе силы трения. , тр. E A , k. E E U 0, U. kтр. E A 2 2 2 1 2 2 k Mv Mv E 2 2 0. 2 2 Mu Mu cos , тр тр. A F S , cos. тр тр. A F S Mg. S
 Решение (продолжение)А 4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0, 02? 2 , 2 k Mu E , тр. A Mg. S , тр. E A 2. 2 Mu Mg. S Отсюда 2 2 , u g. S 2. 2 u S g Подставим в последнюю формулу найденное ранее выражение для скорости конькобежца u : , mv u M 2 2 u m v S g M g 2 2 2 3 8 0, 3. 2 70 2 0, 02 9, 8 m v Sм M g Ответ: S = 0, 3 м.
Решение (продолжение)А 4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед = 0, 02? 2 , 2 k Mu E , тр. A Mg. S , тр. E A 2. 2 Mu Mg. S Отсюда 2 2 , u g. S 2. 2 u S g Подставим в последнюю формулу найденное ранее выражение для скорости конькобежца u : , mv u M 2 2 u m v S g M g 2 2 2 3 8 0, 3. 2 70 2 0, 02 9, 8 m v Sм M g Ответ: S = 0, 3 м.
 Решение. А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 100. Дано: l = 1 м = 100 m 1 =10 00 т 0 — ? События, описанные в задаче, следует разделить на два процесса: 1) абсолютно неупругий удар пули о шар; 2) подъём шара с застрявшей в нём пулей на некоторую высоту. 1. Абсолютно неупругий удар пули и шара. Согласно закону сохранения импульса, 1. mv m m u r r В проекциях на ось OX: 1. mv m m u Отсюда 1. mv u m m
Решение. А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 100. Дано: l = 1 м = 100 m 1 =10 00 т 0 — ? События, описанные в задаче, следует разделить на два процесса: 1) абсолютно неупругий удар пули о шар; 2) подъём шара с застрявшей в нём пулей на некоторую высоту. 1. Абсолютно неупругий удар пули и шара. Согласно закону сохранения импульса, 1. mv m m u r r В проекциях на ось OX: 1. mv m m u Отсюда 1. mv u m m
 Решение (продолжение)А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. 2. Подём пули и шара па высоту h. На шар с пулей действуют только консервативные силы, поэтому изменение механической энергии шара 0. k. E E U 2 2 1 1 2 2 k m m v E 2 2 1 1 0. 2 2 m m u Кинетическая энергия шара с пулей уменьшилась. 1 2 1 1 1. U m m gy m m gh Потенциальная энергия шара с пулей в поле силы тяжести увеличилась.
Решение (продолжение)А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. 2. Подём пули и шара па высоту h. На шар с пулей действуют только консервативные силы, поэтому изменение механической энергии шара 0. k. E E U 2 2 1 1 2 2 k m m v E 2 2 1 1 0. 2 2 m m u Кинетическая энергия шара с пулей уменьшилась. 1 2 1 1 1. U m m gy m m gh Потенциальная энергия шара с пулей в поле силы тяжести увеличилась.
 А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. Решение (продолжение) 1. U m m gh 2 1 , 2 k m m u E 2 1 10. 2 m m u m m gh Отсюда 2. 2 u h g 2 2 1. 22 u m v h gm m g
А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. Решение (продолжение) 1. U m m gh 2 1 , 2 k m m u E 2 1 10. 2 m m u m m gh Отсюда 2. 2 u h g 2 2 1. 22 u m v h gm m g
 А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. Решение (продолжение) 3. Высоту h выразим через угол α из геометрических соображений. Из Δ AO С : cos. OCl h OA l cos , l l h cos 1 cos. h l l l Подставим это в формулу для h : 2 2 2 1 1 cos. 2 m v l m m g Отсюда : 2 12 2 2 1 cos , gl m m v m 12 1 cos. m m v gl m
А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. Решение (продолжение) 3. Высоту h выразим через угол α из геометрических соображений. Из Δ AO С : cos. OCl h OA l cos , l l h cos 1 cos. h l l l Подставим это в формулу для h : 2 2 2 1 1 cos. 2 m v l m m g Отсюда : 2 12 2 2 1 cos , gl m m v m 12 1 cos. m m v gl m
 А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. Решение (продолжение) По условию масса шара в 1000 раз больше массы пули, поэтому в числителе дроби массой пули m можно пренебречь. 12 1 cos. m m v gl m 12 1 cos. m v gl m 12 1 cos 1000 2 9, 8 1 1 cos 10 540. mм v gl mс Ответ: v = 540 м/с.
А 6. Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара пули на угол = 10 0. Решение (продолжение) По условию масса шара в 1000 раз больше массы пули, поэтому в числителе дроби массой пули m можно пренебречь. 12 1 cos. m m v gl m 12 1 cos. m v gl m 12 1 cos 1000 2 9, 8 1 1 cos 10 540. mм v gl mс Ответ: v = 540 м/с.
 Решение. А 7. Стальной шарик массой m = 20 г, падая с высоты h 1 = 1 м на стальную плиту, отскакивает от нее на высоту h 2 = 81 см. Найти импульс p , полученный плитой за время удара, и количество теплоты Q , выделившейся при ударе. Дано: m=20 г h 1 =1 м h 2 =81 см p — ? Q — ? Импульс, полученный плитой при ударе, определим из закона сохранения импульса: 1 2, p p p r r r 1 p r 2 p r импульс шара перед ударом; импульс шара после удара. импульс, полученный плитой; 1 2. p p p r r r В проекциях но ось OY : 1 2. p p p , yp p 1 1, yp p 2 2, yp p Величина импульса, полученного плитой 1 2, p p p mv mv 2 v 1 v величина скорости шара после удара. величина скорости шара перед ударом;
Решение. А 7. Стальной шарик массой m = 20 г, падая с высоты h 1 = 1 м на стальную плиту, отскакивает от нее на высоту h 2 = 81 см. Найти импульс p , полученный плитой за время удара, и количество теплоты Q , выделившейся при ударе. Дано: m=20 г h 1 =1 м h 2 =81 см p — ? Q — ? Импульс, полученный плитой при ударе, определим из закона сохранения импульса: 1 2, p p p r r r 1 p r 2 p r импульс шара перед ударом; импульс шара после удара. импульс, полученный плитой; 1 2. p p p r r r В проекциях но ось OY : 1 2. p p p , yp p 1 1, yp p 2 2, yp p Величина импульса, полученного плитой 1 2, p p p mv mv 2 v 1 v величина скорости шара после удара. величина скорости шара перед ударом;
 Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Скорости шара определим из закона сохранения энергии. 1. Рассмотрим процесс падения шара. Если пренебречь силой сопротивления воздуха, то на шар действует только консервативная сила тяжести. Поэтому изменение полной механической энергии равно нулю. 0. k. E E U 22 01 2 2 k mvmv E 2 2 1 10. 2 2 mv mv 1 0. U mgy mg. H Кинетическая энергия шара увеличилась. Потенциальная энергия шара в поле силы тяжести уменьшилась. 2 10. 2 mv E mg. H 2 1, 2 mv mg. H 12. v g. H
Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Скорости шара определим из закона сохранения энергии. 1. Рассмотрим процесс падения шара. Если пренебречь силой сопротивления воздуха, то на шар действует только консервативная сила тяжести. Поэтому изменение полной механической энергии равно нулю. 0. k. E E U 22 01 2 2 k mvmv E 2 2 1 10. 2 2 mv mv 1 0. U mgy mg. H Кинетическая энергия шара увеличилась. Потенциальная энергия шара в поле силы тяжести уменьшилась. 2 10. 2 mv E mg. H 2 1, 2 mv mg. H 12. v g. H
 Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. 2. Рассмотрим процесс подъёма шара. Если пренебречь силой сопротивления воздуха, то на шар действует только консервативная сила тяжести. Поэтому изменение полной механической энергии равно нулю. 0. k. E E U 22 32 2 2 k mvmv E 2 20. 2 2 mv mv 3 2. U mgy mgh Кинетическая энергия шара уменьшилась. Потенциальная энергия шара в поле силы тяжести увеличилась. 2 20. 2 mv E mgh 2 2, 2 mv mgh 22. v gh
Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. 2. Рассмотрим процесс подъёма шара. Если пренебречь силой сопротивления воздуха, то на шар действует только консервативная сила тяжести. Поэтому изменение полной механической энергии равно нулю. 0. k. E E U 22 32 2 2 k mvmv E 2 20. 2 2 mv mv 3 2. U mgy mgh Кинетическая энергия шара уменьшилась. Потенциальная энергия шара в поле силы тяжести увеличилась. 2 20. 2 mv E mgh 2 2, 2 mv mgh 22. v gh
 Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Величина импульса, полученная плитой: 22. v gh 12 , v g. H 1 2, p mv mv 1 22 2 2. p mv mv m g. H gh m g H h 2 0, 02 2 9, 8 1 0, 81 0, 17. кг м p m g H h с
Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Величина импульса, полученная плитой: 22. v gh 12 , v g. H 1 2, p mv mv 1 22 2 2. p mv mv m g. H gh m g H h 2 0, 02 2 9, 8 1 0, 81 0, 17. кг м p m g H h с
 Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Выделившееся количество тепла определим из закона сохранения энергии. 3. Рассмотрим неупругий удар шара. На шар кроме консервативной силы упругости действуют неконсервативные силы. Поэтому изменение полной механической энергии не равно нулю. Будем считать, что вся выделившаяся энергия перешла в тепло. . k. E E U Q 2 2 2 1, 2 2 k mv mv E 0. U 2 2 2 1. 2 2 mv mv Q 2 2 m gh m g. H Q mg h H 0, 02 9, 8 0, 81 1 0, 037. Q mg h HДж Знак «-» указывает на то, что энергия системы уменьшилась, то есть тепло выделилось. Ответ: p = 0, 17 (кг·м)/с; Δ Q = — 0, 037 Дж.
Решение (продолжение)А 7. Стальной шарик массой m=20 г, падая с высоты h 1 =1 м на стальную плиту, отскакивает от нее на высоту h 2 =81 см. Найти импульс p, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Выделившееся количество тепла определим из закона сохранения энергии. 3. Рассмотрим неупругий удар шара. На шар кроме консервативной силы упругости действуют неконсервативные силы. Поэтому изменение полной механической энергии не равно нулю. Будем считать, что вся выделившаяся энергия перешла в тепло. . k. E E U Q 2 2 2 1, 2 2 k mv mv E 0. U 2 2 2 1. 2 2 mv mv Q 2 2 m gh m g. H Q mg h H 0, 02 9, 8 0, 81 1 0, 037. Q mg h HДж Знак «-» указывает на то, что энергия системы уменьшилась, то есть тепло выделилось. Ответ: p = 0, 17 (кг·м)/с; Δ Q = — 0, 037 Дж.
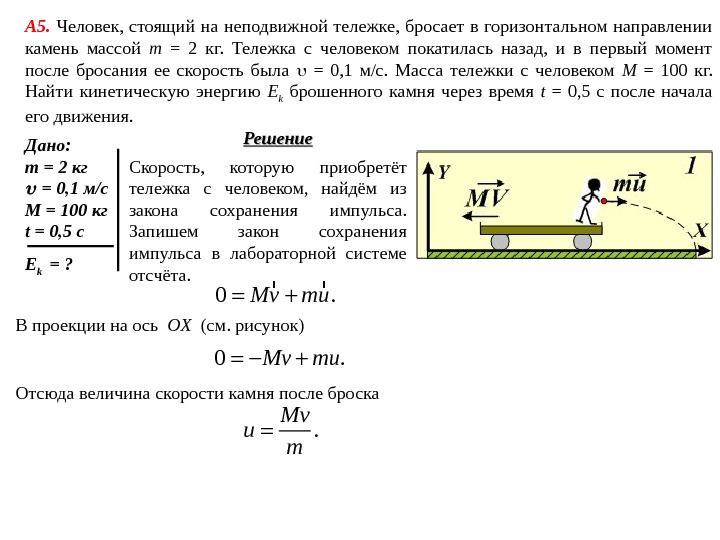
 А 5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0, 1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию E k брошенного камня через время t = 0, 5 с после начала его движения. Дано: m = 2 кг = 0, 1 м/с M = 100 кг t = 0, 5 с E k = ? Решение Скорость, которую приобретёт тележка с человеком, найдём из закона сохранения импульса. Запишем закон сохранения импульса в лабораторной системе отсчёта. 0. Mv mu r r В проекции на ось OX ( см. рисунок) 0. Mv mu Отсюда величина скорости камня после броска . Mv u m
А 5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0, 1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию E k брошенного камня через время t = 0, 5 с после начала его движения. Дано: m = 2 кг = 0, 1 м/с M = 100 кг t = 0, 5 с E k = ? Решение Скорость, которую приобретёт тележка с человеком, найдём из закона сохранения импульса. Запишем закон сохранения импульса в лабораторной системе отсчёта. 0. Mv mu r r В проекции на ось OX ( см. рисунок) 0. Mv mu Отсюда величина скорости камня после броска . Mv u m
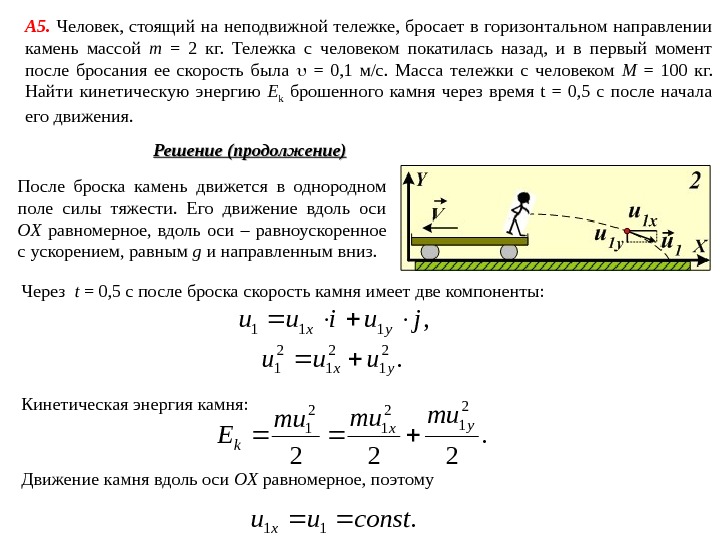
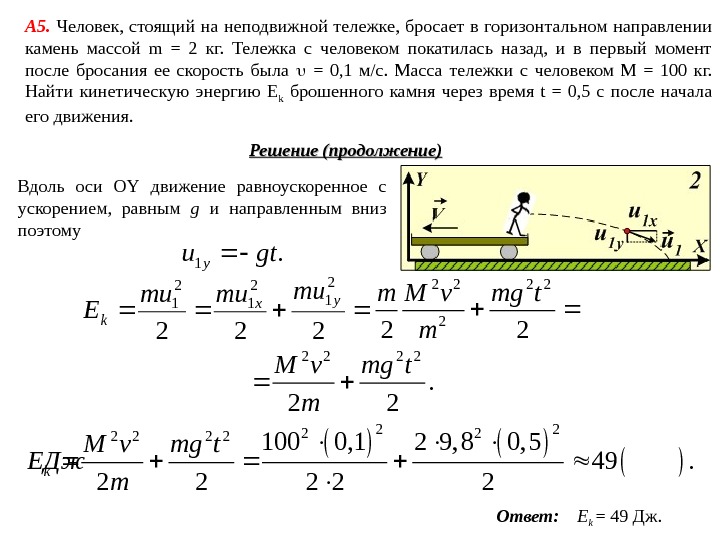
 А 5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0, 1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию E k брошенного камня через время t = 0, 5 с после начала его движения. Решение (продолжение) После броска камень движется в однородном поле силы тяжести. Его движение вдоль оси OX равномерное, вдоль оси – равноускоренное с ускорением, равным g и направленным вниз. Через t = 0, 5 с после броска скорость камня имеет две компоненты: , 111 juiuu yx . 2 12 12 1 yxuuu Кинетическая энергия камня: . 222 2 12 12 1 y x k mumumu E Движение камня вдоль оси OX равномерное, поэтому . 11 constuu x
А 5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0, 1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию E k брошенного камня через время t = 0, 5 с после начала его движения. Решение (продолжение) После броска камень движется в однородном поле силы тяжести. Его движение вдоль оси OX равномерное, вдоль оси – равноускоренное с ускорением, равным g и направленным вниз. Через t = 0, 5 с после броска скорость камня имеет две компоненты: , 111 juiuu yx . 2 12 12 1 yxuuu Кинетическая энергия камня: . 222 2 12 12 1 y x k mumumu E Движение камня вдоль оси OX равномерное, поэтому . 11 constuu x
 А 5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0, 1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию E k брошенного камня через время t = 0, 5 с после начала его движения. Ответ: E k = 49 Дж. Решение (продолжение) Вдоль оси OY движение равноускоренное с ускорением, равным g и направленным вниз поэтому. 1 gtuy 222 2 12 12 1 y x k mu mumu E 2 2 2 2 m M v mg t m 2 2 M v mg t m 2 22 22 2 100 0, 1 2 9, 8 0, 5 49. 2 2 2 k. M v mg t E Дж m »
А 5. Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент после бросания ее скорость была = 0, 1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию E k брошенного камня через время t = 0, 5 с после начала его движения. Ответ: E k = 49 Дж. Решение (продолжение) Вдоль оси OY движение равноускоренное с ускорением, равным g и направленным вниз поэтому. 1 gtuy 222 2 12 12 1 y x k mu mumu E 2 2 2 2 m M v mg t m 2 2 M v mg t m 2 22 22 2 100 0, 1 2 9, 8 0, 5 49. 2 2 2 k. M v mg t E Дж m »
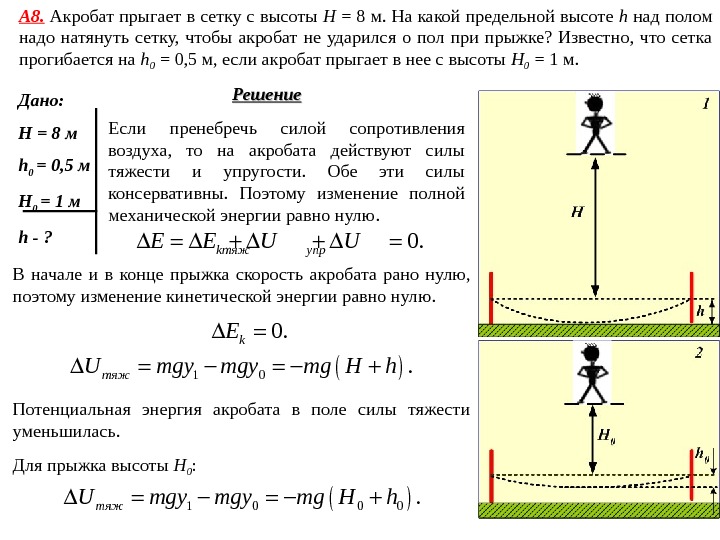
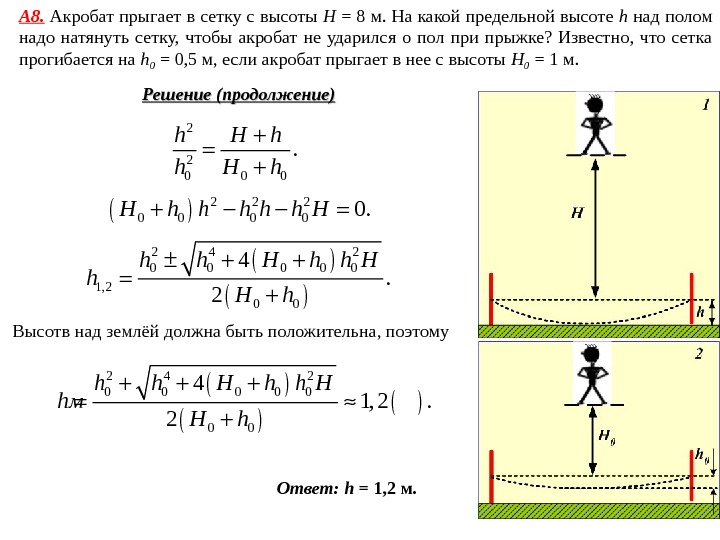
 А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Дано: Н = 8 м h 0 = 0, 5 м H 0 = 1 м h — ? Решение Если пренебречь силой сопротивления воздуха, то на акробата действуют силы тяжести и упругости. Обе эти силы консервативны. Поэтому изменение полной механической энергии равно нулю. 0. k тяж упр. E E U U В начале и в конце прыжка скорость акробата рано нулю, поэтому изменение кинетической энергии равно нулю. 0. k. E 1 0. тяж. U mgy mg H h Потенциальная энергия акробата в поле силы тяжести уменьшилась. 1 0 0 0. тяж. U mgy mg H h Для прыжка высоты H 0 :
А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Дано: Н = 8 м h 0 = 0, 5 м H 0 = 1 м h — ? Решение Если пренебречь силой сопротивления воздуха, то на акробата действуют силы тяжести и упругости. Обе эти силы консервативны. Поэтому изменение полной механической энергии равно нулю. 0. k тяж упр. E E U U В начале и в конце прыжка скорость акробата рано нулю, поэтому изменение кинетической энергии равно нулю. 0. k. E 1 0. тяж. U mgy mg H h Потенциальная энергия акробата в поле силы тяжести уменьшилась. 1 0 0 0. тяж. U mgy mg H h Для прыжка высоты H 0 :
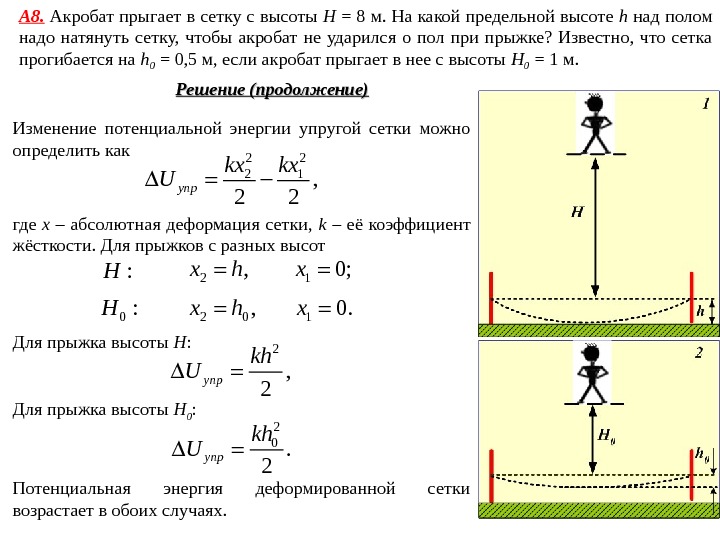
 А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Решение (продолжение) Изменение потенциальной энергии упругой сетки можно определить как 2 2 2 1 , 2 2 упр kx kx U где x – абсолютная деформация сетки, k – её коэффициент жёсткости. Для прыжков с разных высот 2, x h 2 0, x h 10; x 10. x : H 0: H Для прыжка высоты H : 2 , 2 упр kh U Для прыжка высоты H 0 : 2 0. 2 упр kh U Потенциальная энергия деформированной сетки возрастает в обоих случаях.
А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Решение (продолжение) Изменение потенциальной энергии упругой сетки можно определить как 2 2 2 1 , 2 2 упр kx kx U где x – абсолютная деформация сетки, k – её коэффициент жёсткости. Для прыжков с разных высот 2, x h 2 0, x h 10; x 10. x : H 0: H Для прыжка высоты H : 2 , 2 упр kh U Для прыжка высоты H 0 : 2 0. 2 упр kh U Потенциальная энергия деформированной сетки возрастает в обоих случаях.
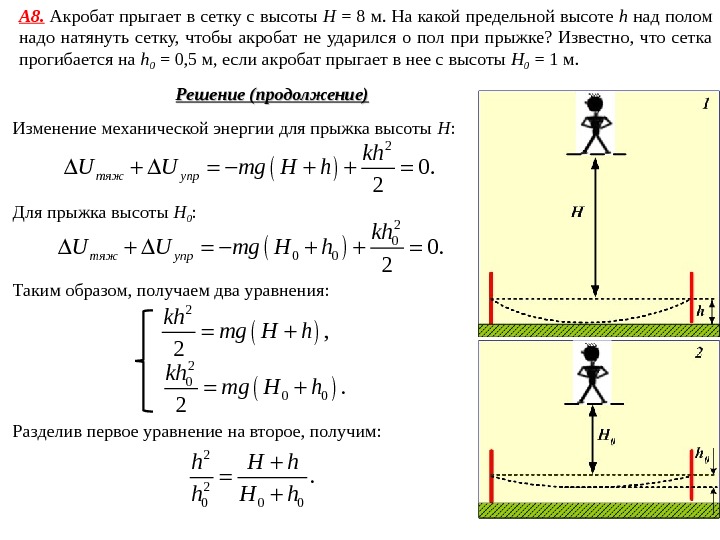
 А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Решение (продолжение) Изменение механической энергии для прыжка высоты H : 2 0. 2 тяж упр kh U U mg H h Для прыжка высоты H 0 : 2 0 0. 2 тяж упр kh U U mg H h Таким образом, получаем два уравнения : 2 , 2 kh mg H h 2 0 0 0. 2 kh mg H h Разделив первое уравнение на второе, получим : 2 2 0 0 0. h H h
А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Решение (продолжение) Изменение механической энергии для прыжка высоты H : 2 0. 2 тяж упр kh U U mg H h Для прыжка высоты H 0 : 2 0 0. 2 тяж упр kh U U mg H h Таким образом, получаем два уравнения : 2 , 2 kh mg H h 2 0 0 0. 2 kh mg H h Разделив первое уравнение на второе, получим : 2 2 0 0 0. h H h
 А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Ответ: h = 1, 2 м. Решение (продолжение) 2 2 0 0 0. h H h 2 2 2 0 00. H h h h H 2 4 2 0 0 0 1, 2 0 0 4. 2 h h H h H h Высотв над землёй должна быть положительна, поэтому 2 4 2 0 0 0 0 4 1, 2. 2 h h H hм H h
А 8. Акробат прыгает в сетку с высоты Н = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h 0 = 0, 5 м, если акробат прыгает в нее с высоты H 0 = 1 м. Ответ: h = 1, 2 м. Решение (продолжение) 2 2 0 0 0. h H h 2 2 2 0 00. H h h h H 2 4 2 0 0 0 1, 2 0 0 4. 2 h h H h H h Высотв над землёй должна быть положительна, поэтому 2 4 2 0 0 0 0 4 1, 2. 2 h h H hм H h
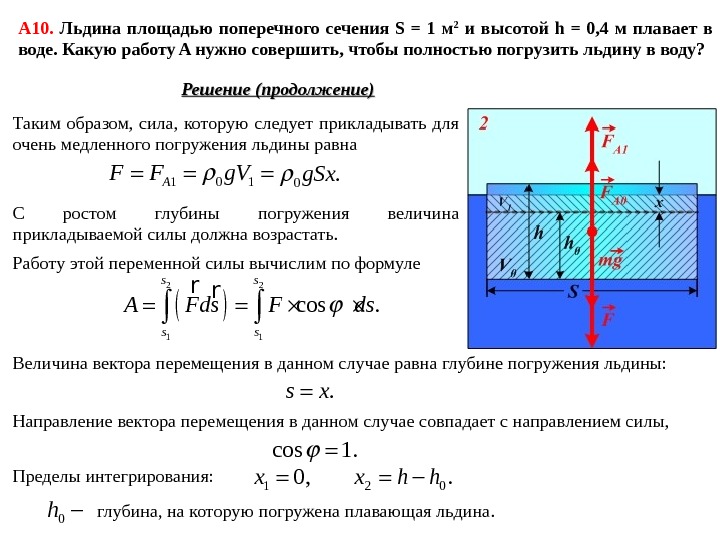
 А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Дано: S = 1 м 2 h = 0, 4 м A = ? Решение Первоначально льдина плавает, то есть находится в положении равновесия. Векторная сумма сил, приложенных к льдине, равна нулю. 00. Amg F rr Здесь F A 0 – сила Архимеда, действующая на льдину в положении равновесия. Величина этой силы 0 0 0, AF g. V где 0 – плотность воды, V 0 – объём части льдины, погружённой в воду. По мере погружения льдины в воду объём погружённой части будет расти. Следовательно, будет расти и сила Архимеда, действующая на льдину. Если мы хотим погружать льдину очень медленно (без возрастания её кинетической энергии), то мы должны прикладывать к ней такую внешнюю силу F , чтобы в каждый момент времени можно было считать, что льдина находится в равновесии.
А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Дано: S = 1 м 2 h = 0, 4 м A = ? Решение Первоначально льдина плавает, то есть находится в положении равновесия. Векторная сумма сил, приложенных к льдине, равна нулю. 00. Amg F rr Здесь F A 0 – сила Архимеда, действующая на льдину в положении равновесия. Величина этой силы 0 0 0, AF g. V где 0 – плотность воды, V 0 – объём части льдины, погружённой в воду. По мере погружения льдины в воду объём погружённой части будет расти. Следовательно, будет расти и сила Архимеда, действующая на льдину. Если мы хотим погружать льдину очень медленно (без возрастания её кинетической энергии), то мы должны прикладывать к ней такую внешнюю силу F , чтобы в каждый момент времени можно было считать, что льдина находится в равновесии.
 А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Пусть льдина погружена на некоторую глубину x. По сравнению с положением равновесия сила Архимеда возросла. 0 1, A A AF F F r r r Векторная сумма сил, приложенных к льдине, равна нулю. 0 0 1, AF g. V 1 V Sx — объём, ушедший под воду в процессе принудительного погружения льдины под действием силы F. 0 10. A Amg F F F r r rr В проекции на вертикальную ось, направленную вверх, 0 10. A Amg F F F Но, как было показано ранее, 00, Amg F поэтому, 1.
А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Пусть льдина погружена на некоторую глубину x. По сравнению с положением равновесия сила Архимеда возросла. 0 1, A A AF F F r r r Векторная сумма сил, приложенных к льдине, равна нулю. 0 0 1, AF g. V 1 V Sx — объём, ушедший под воду в процессе принудительного погружения льдины под действием силы F. 0 10. A Amg F F F r r rr В проекции на вертикальную ось, направленную вверх, 0 10. A Amg F F F Но, как было показано ранее, 00, Amg F поэтому, 1.
 А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Таким образом, сила, которую следует прикладывать для очень медленного погружения льдины равна 1 0 1 AF F g. V 0. g. Sx С ростом глубины погружения величина прикладываемой силы должна возрастать. Работу этой переменной силы вычислим по формуле 2 2 1 1 cos. s s. A Fds F ds r r Величина вектора перемещения в данном случае равна глубине погружения льдины: . s x Направление вектора перемещения в данном случае совпадает с направлением силы, cos 1. Пределы интегрирования: 10, x 2 0. x h h 0 h глубина, на которую погружена плавающая льдина.
А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Таким образом, сила, которую следует прикладывать для очень медленного погружения льдины равна 1 0 1 AF F g. V 0. g. Sx С ростом глубины погружения величина прикладываемой силы должна возрастать. Работу этой переменной силы вычислим по формуле 2 2 1 1 cos. s s. A Fds F ds r r Величина вектора перемещения в данном случае равна глубине погружения льдины: . s x Направление вектора перемещения в данном случае совпадает с направлением силы, cos 1. Пределы интегрирования: 10, x 2 0. x h h 0 h глубина, на которую погружена плавающая льдина.
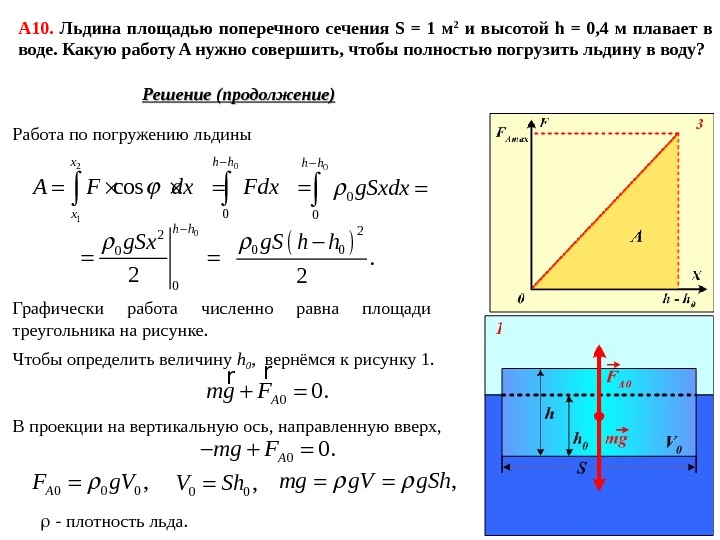
 А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Работа по погружению льдины 0 2 10 cos h hx x. A F dx Fdx 0 0 0 h h g. Sxdx 0 2 0 02 h h g. Sx 2 0 0. 2 g. S h h Графически работа численно равна площади треугольника на рисунке. Чтобы определить величину h 0 , вернёмся к рисунку 1. 00. Amg F rr 0 0 0, AF g. V 0 0, V Sh В проекции на вертикальную ось, направленную вверх, 00. Amg F , mg g. V g. Sh — плотность льда.
А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Работа по погружению льдины 0 2 10 cos h hx x. A F dx Fdx 0 0 0 h h g. Sxdx 0 2 0 02 h h g. Sx 2 0 0. 2 g. S h h Графически работа численно равна площади треугольника на рисунке. Чтобы определить величину h 0 , вернёмся к рисунку 1. 00. Amg F rr 0 0 0, AF g. V 0 0, V Sh В проекции на вертикальную ось, направленную вверх, 00. Amg F , mg g. V g. Sh — плотность льда.
 А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Окончательно, работа по погружению льдины 2 20 00 0. 2 2 g. S h h A 0 0 0, AF g. V 0 0, V Sh 00. Amg F , mg g. V g. Sh 0 0. g. Sh Sh 0 0. h h 2 2 0 07, 84. 2 g. Sh AДж Ответ: А = 7, 84 Дж.
А 10. Льдина площадью поперечного сечения S = 1 м 2 и высотой h = 0, 4 м плавает в воде. Какую работу A нужно совершить, чтобы полностью погрузить льдину в воду? Решение (продолжение) Окончательно, работа по погружению льдины 2 20 00 0. 2 2 g. S h h A 0 0 0, AF g. V 0 0, V Sh 00. Amg F , mg g. V g. Sh 0 0. g. Sh Sh 0 0. h h 2 2 0 07, 84. 2 g. Sh AДж Ответ: А = 7, 84 Дж.

