Презентация file 20100112173702

Функция у=ах 2 и ее свойства.

Цели : ввести понятие квадратичной функции ; научится строить график функции у=ах2 и описывать свойства данной функции по графику ; установить закономерность между графиком функции у=ах 2 и значением коэффициента а.

Определение. Квадратичной функцией называется функция, которую можно задать формулой вида у=ах2 + bx+c, где х – независимая переменная, а, b и с – некоторые числа, причем а ≠ 0.

Из приведенных примеров укажите те функции, которые являются квадратичными. Для квадратичных функций назовите коэффициенты. 1 x 5 y 1 x 3 y 2 1 x 2 y 2 3 xx 2 y 2 1 x 7 xy 3 2 x 4 y xx 2 y 2 1 4 x y

Функция у=ах 2 , ее график и свойства.

ХУ 1149 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 2 xy 1) х -3 -2 -1 0 1 2 3 у

ХУ 1149 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 2 xy 1) х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у > 0, если х ; 00;

ХУ 1149 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 2 xy 1) х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у > 0, если х ; 00; 4. у ↓ , если х 0; у ↑ , если х ;

ХУ 1149 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 2 xy 1) х -3 -2 -1 0 1 2 3 у 9 4 1 0 1 4 9 1. D(y): R 2. у=0, если х=0 3. у > 0, если х ; 00; 4. у ↓ , если х 0; у ↑ , если х ; 0 5. у наим =0, если х=0 у наиб – не существует. 6. Е (y): ;

ХУ 1149 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 2) х -3 -2 -1 0 1 2 3 у 18 8 2 0 2 8 182 x 2 y Есть ли различия в свойствах по сравнению с предыдущей функцией ? Чем отличается график ?

График функции у= kx 2 может быть получен из графика функции у= x 2 путем растяжения его вдоль оси Оу в k раз (k- натуральное число ).

ХУ 1149 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 3) х -3 -2 -1 0 1 2 3 у 4, 5 2 0, 5 0 0, 5 2 4, 5 2 x 2 1 y Есть ли различия в свойствах по сравнению с первой функцией ? Чем отличается график ?

График функции у= x 2 может быть получен из графика функции у= x 2 путем сжатия его вдоль оси Оу в k раз (k- натуральное число ). k

ХУ 11 -2 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 4) х -3 -2 -1 0 1 2 3 у -4, 5 -2 -0, 5 0 -0, 5 -2 -4, 5 Есть ли различия в свойствах по сравнению с предыдущей функцией ? 2 x 2 1 y

ХУ 11 -2 2 3 -1 Построим графики функций 2 xy 2 x 2 1 y и исследуем их свойства. 4) х -3 -2 -1 0 1 2 3 у -4, 5 -2 -0, 5 0 -0, 5 -2 -4, 52 x 2 1 y 1. D(y): R 2. у=0, если х=0 3. у < 0, если х ; 00; 4. у ↑ , если х 0; у ↓ , если х ; 0 5. у наиб =0, если х=0 у наим – не существует. 6. Е (y): 0;

График функции у=ах2 симметричен графику функции у=-ах 2 относительно оси Ох. Если а > 0, то ветви параболы направлены… Если а < 0, то ветви параболы направлены…

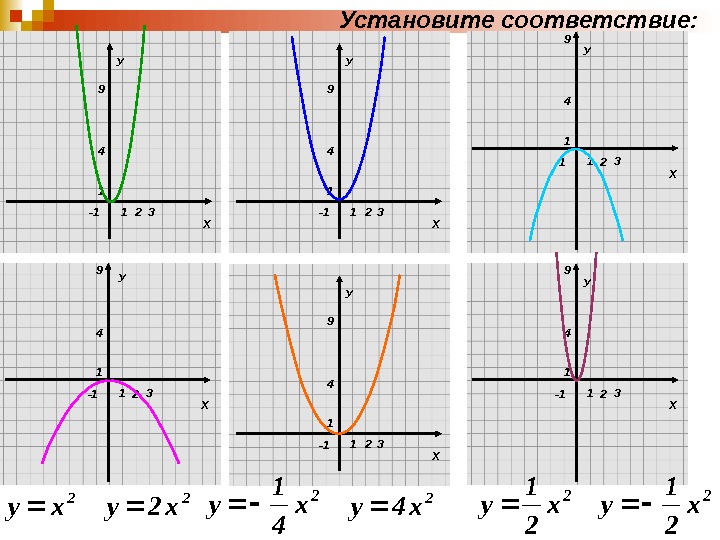
ХУ 1149 2 3 -1 2 Х 1149 3 -1 ХУ 1149 2 3 -12 Х 1149 3 -12 xy 2 x 2 y 2 x 4 1 y 2 x 4 y 2 x 2 1 y У У УУстановите соответствие :