Преобразование комплексного чертежа
Способ замены плоскостей проекций Геометрический объект в пространстве остается неподвижным, изменяет положение аппарат проецирования Способ вращения Геометрический объект изменяет свое положение в пространстве, аппарат проецирования остается неподвижным
Cпособ замены плоскостей проекций 4 основные задачи
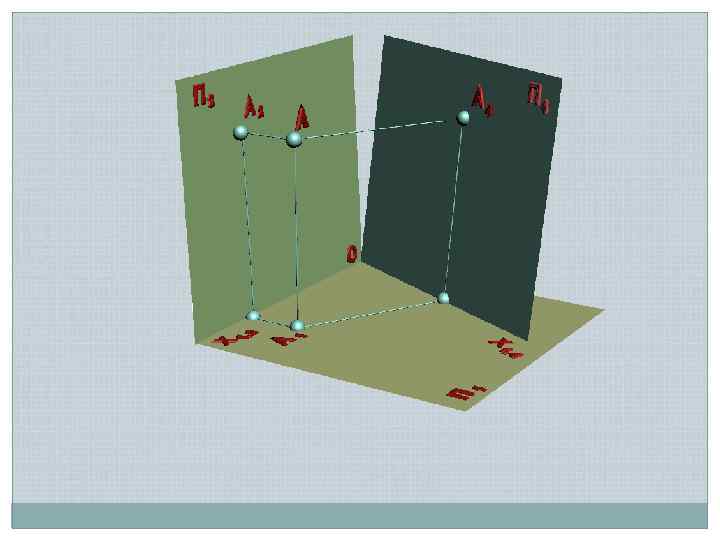
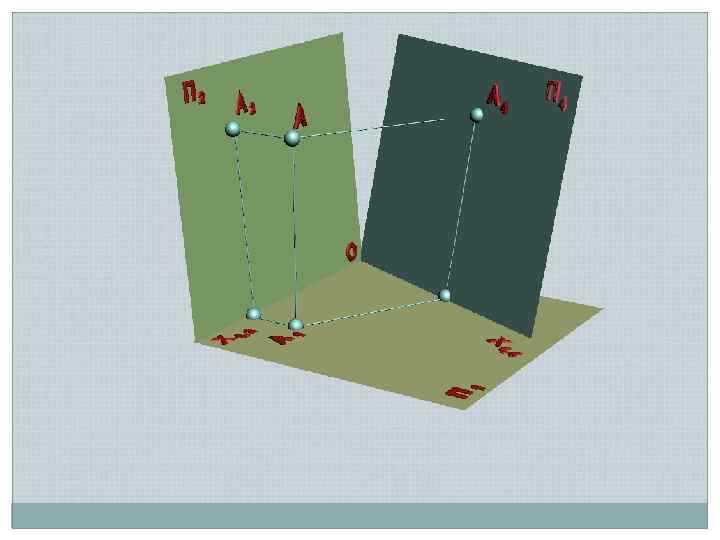
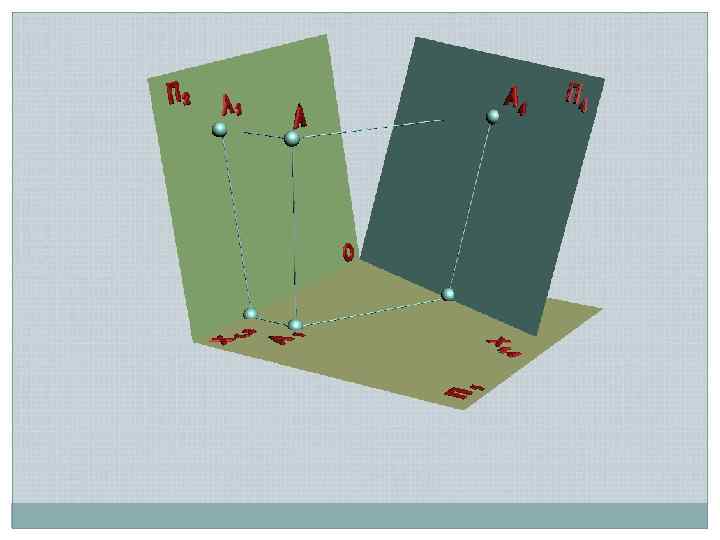
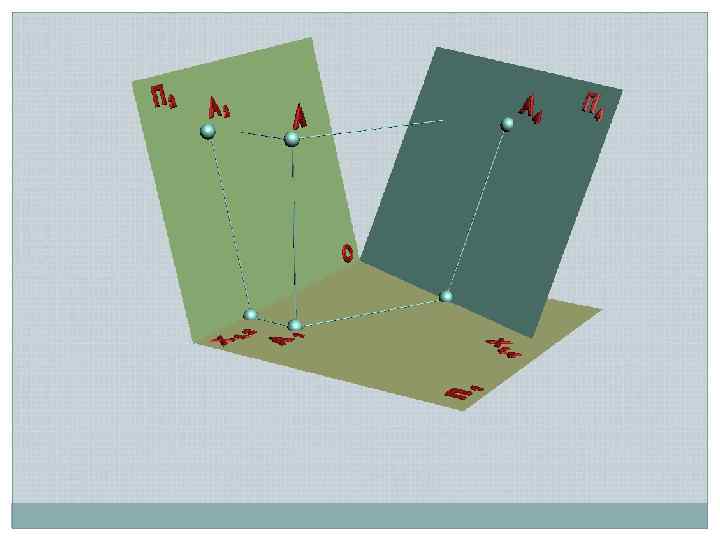
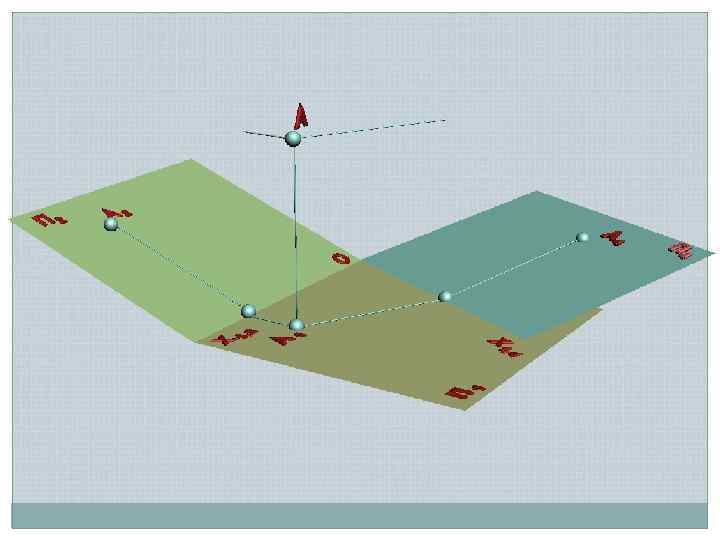
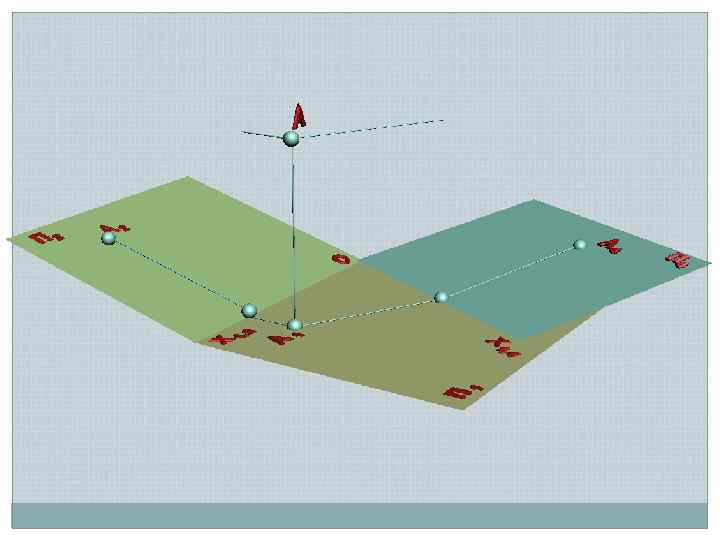
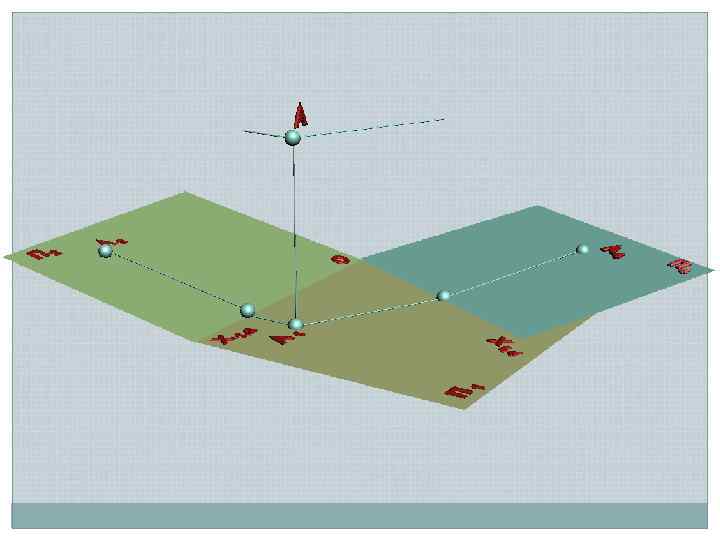
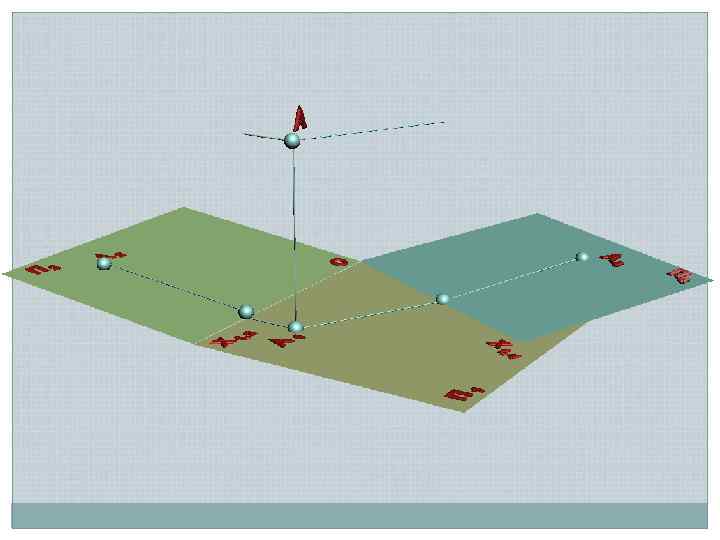
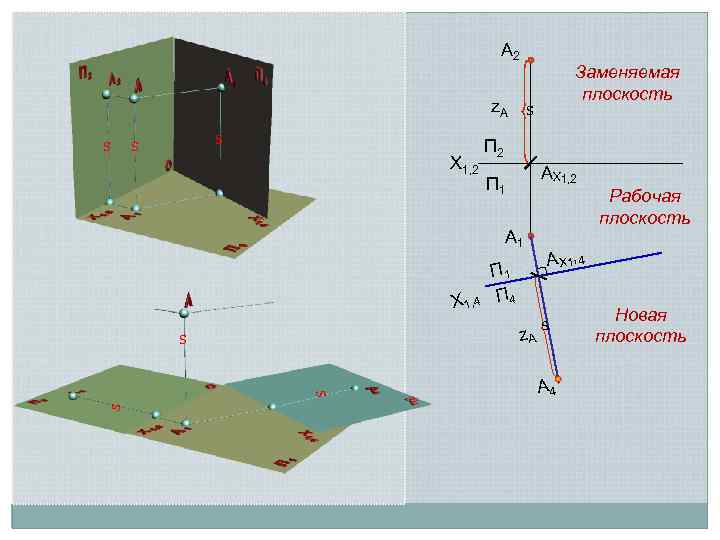
А 2 z. A s s s Х 1, 2 s П 2 АХ 1, 2 П 1 А 1 Х 1, 4 s s П 1 П 4 z. A s Заменяемая плоскость Рабочая плоскость АХ 1, 4 s А 4 Новая плоскость
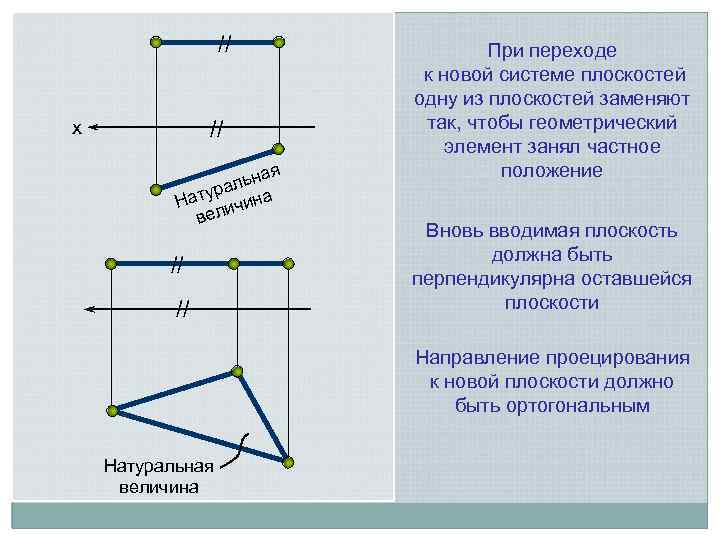
// // х ая льн а атур чина Н и вел // // При переходе к новой системе плоскостей одну из плоскостей заменяют так, чтобы геометрический элемент занял частное положение Вновь вводимая плоскость должна быть перпендикулярна оставшейся плоскости Направление проецирования к новой плоскости должно быть ортогональным Натуральная величина
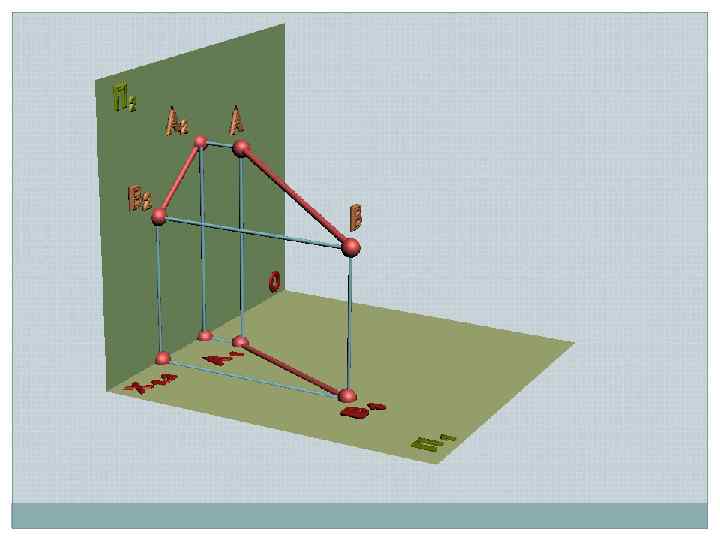
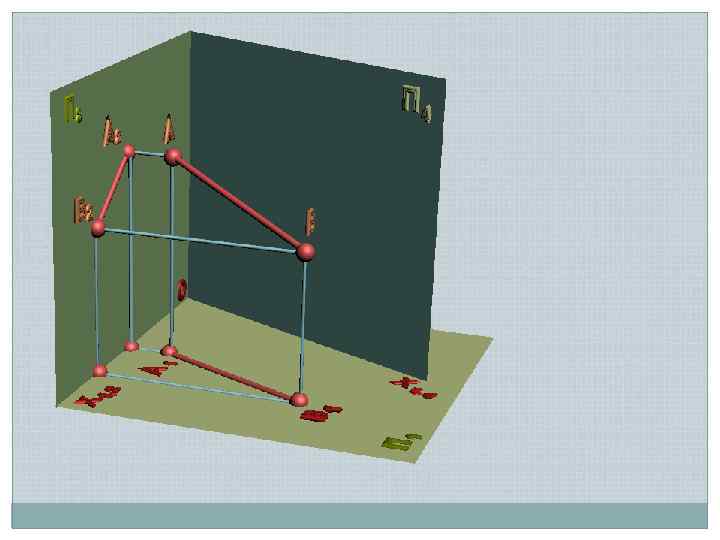
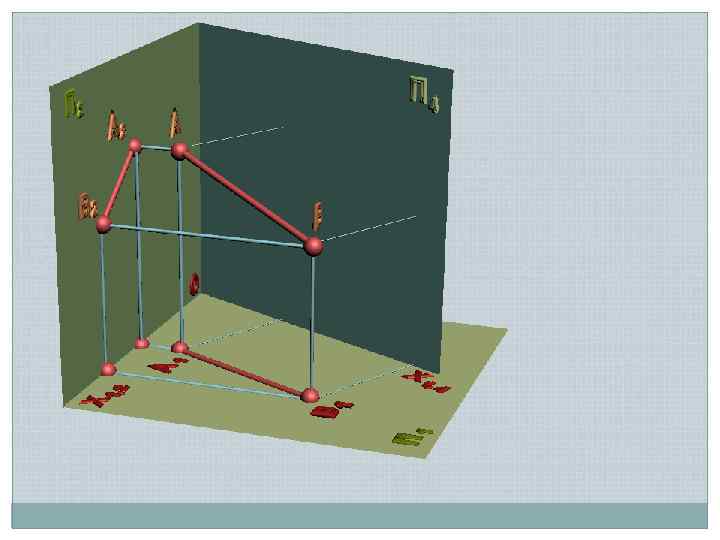
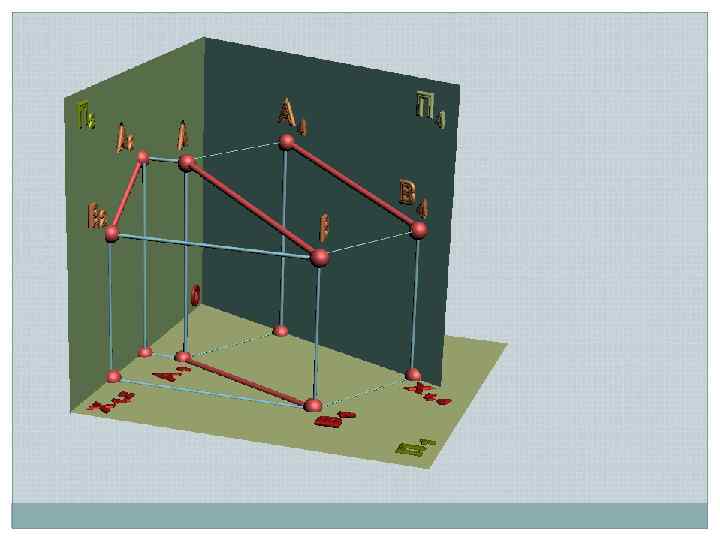
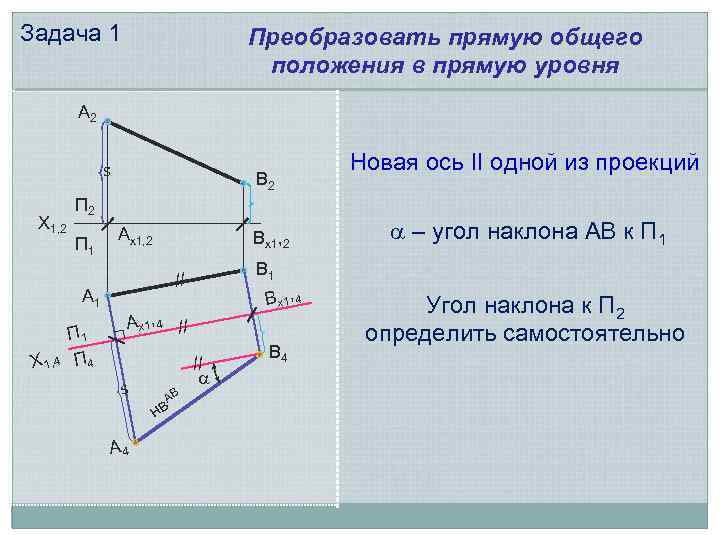
Задача 1 Преобразовать прямую общего положения в прямую уровня А 2 s Х 1, 2 П 1 А 1 Х 1, 4 В 2 П 1 П 4 Ах1, 2 В х1, 4 // // s А 4 АВ нв – угол наклона АВ к П 1 В 1 // А х1, 4 Новая ось ІІ одной из проекций В 4 Угол наклона к П 2 определить самостоятельно
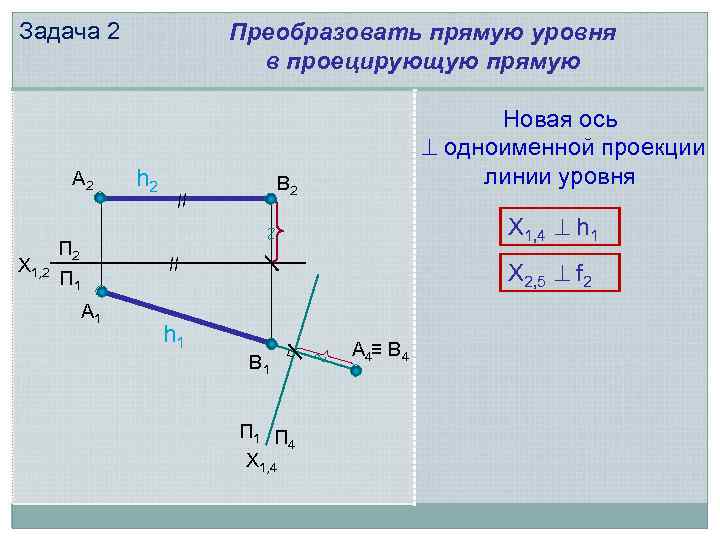
Задача 2 А 1 h 2 Новая ось ^ одноименной проекции линии уровня В 2 // Х 1, 4 ^ h 1 ∿ Х 1, 2 П 1 Преобразовать прямую уровня в проецирующую прямую // h 1 Х 2, 5 ^ f 2 В 1 П 4 Х 1, 4 ∿ А 4≡ В 4
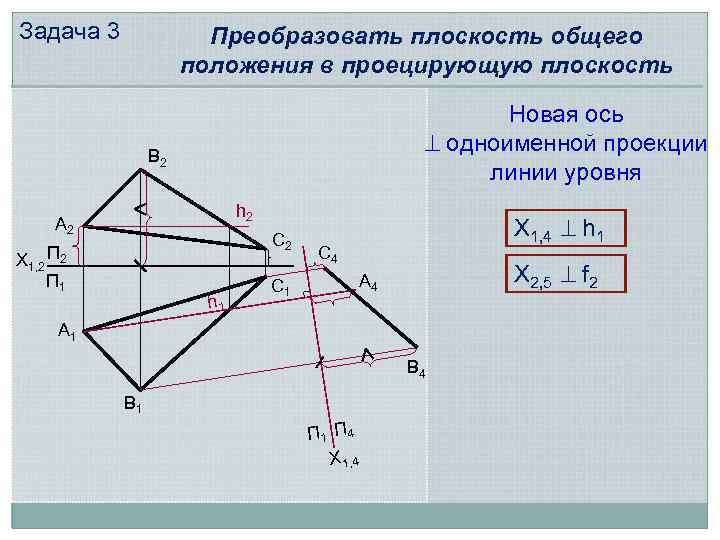
Задача 3 Преобразовать плоскость общего положения в проецирующую плоскость Новая ось ^ одноименной проекции линии уровня В 2 h 2 А 2 С 2 Х 1, 2 П 1 h 1 С 1 Х 1, 4 ^ h 1 С 4 Х 2, 5 ^ f 2 А 4 А 1 В 4 В 1 П 4 Х 1, 4
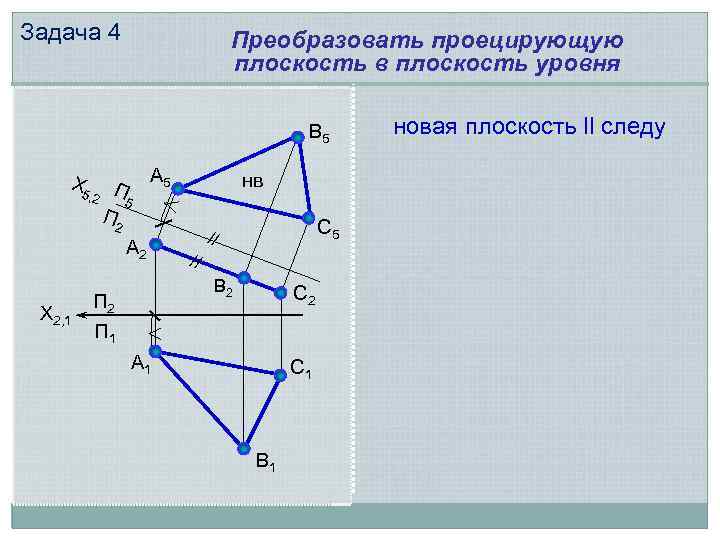
Задача 4 Преобразовать проецирующую плоскость в плоскость уровня В 5 Х 5 , 2 П 5 П 2 А 5 А 2 Х 2, 1 нв С 5 // // В 2 П 1 С 2 А 1 С 1 В 1 новая плоскость ll следу
10 задач, которые можно решить методом замены плоскостей проекций:
1. Определение натуральной величины отрезка (см. основную задачу 1) 2. Определение расстояния от точки до прямой (прямую преобразовать в проецирующую) 3. Определение расстояния между параллельными прямыми (прямые преобразовать в проецирующие) 4. Определение величины двугранного угла (общее ребро преобразовать в проецирующую прямую) 5. Определение расстояния между скрещивающими прямыми (одну из прямых преобразовать в проецирующую)
6. Определение расстояния от точки до плоскости (плоскость преобразовать в след) 7. Определение расстояния между параллельными плоскостями (обе плоскости преобразовать в след) 8. Определение натуральной величины плоской фигуры (см. основную задачу 4 ) 9. Определение угла наклона прямой к плоскости (см. основную задачу 1 ) 10. Определение угла наклона плоскости к плоскостям проекций (см. основную задачу 3 )
Скачать презентацию Преобразование комплексного чертежа Способ замены плоскостей проекций
Преобразование комплексного чертежа.ppt