Предмет начертательной геометрии Начертательная геометрия входит в

Предмет начертательной геометрии • Начертательная геометрия входит в число дисциплин, составляющих основу инженерного образования. Таким образом, начертательная геометрия является теоретической основой изготовления чертежей и чтения этих основополагающих технических документов. • Начертательная геометрия является первой составной частью общеинженерной учебной дисциплины – инженерной графики, включающей в себя также техническое черчение и компьютерную графику.

История начертательной геометрии • В России начертательная геометрия преподается с 1810 г. впервые в Петербургском Институте корпуса инженеров путей сообщения. В этом высшем учебном заведении преподавал Яков Александрович Севастьянов (1796 – 1846). С его именем связано появление первых сочинений по начертательной геометрии в нашей стране, сначала переведенных с французского языка, а затем оригинального труда "Основания начертательной геометрии" (1821 г. ). • Значительный вклад в развитие начертательной геометрии внесли Николай Иванович Макаров (1824– 1904)– профессор Петербургского технологического института и Валериан Иванович Курдюмов (1853– 1904)–профессор Петербургского Института инженеров путей сообщения. • Дальнейшее развитие научного содержания начертательной геометрии получило в трудах Евграфа Степановича Федорова (1853 – 1919), Николая Алексеевича Рынина (1877 – 1942). • В настоящее время начертательная геометрия в качестве научной и учебной дисциплины окончательно сформировалась трудами Н. А. Глаголева (1888 – 1945), А. И. Добрякова (1895 – 1947), С. М. Колотова (1888 – 1965), И. И. Котова (1909 – 1976) и многих других.

Геометрические области Плоскость проекций: p – произвольная; p 1 – горизонтальная; p 2 – фронтальная; p 3 – профильная; S – центр проецирования. Оси проекции: X – ось абсцисс; Y – ось ординат; Z – ось аппликат; Начало координат – прописной буквой О. Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита, а также арабскими цифрами: A, B, C, D, …, L, M, N, 1, 2, 3, 4, …, 12, 13, 14, … Линии, расположенные произвольно относительно плоскостей проекций, обозначаются строчными буквами латинского алфавита: a, b, c, …, l, m, n

Геометрические области Линии уровня обозначаются: h – горизонталь; f – фронталь; p – профильная прямая. Для прямых линий используются также следующие обозначения: (A, B) – прямая, проходящая через точки A и B; [AB] – отрезок прямой, ограниченный точками А и В Плоскости обозначаются прописными буквами латинского и греческого алфавита: P, Q, R, S, T… Для обозначения плоскостей уровня используются прописные буквы только греческого алфавита: Г – горизонтальная плоскость (гамма); Ф – фронтальная плоскость (фи); Р – профильная плоскость (ро). Чтобы выделить способ задания плоскости, указывают ее геометрические элементы, которыми она определяется: • P (ΔABC) – плоскость P задана треугольником ABC; • • Q (a b) – плоскость Q задана пересекающимися прямыми a и b; R (m II n) – плоскость R задана параллельными прямыми m и n; • S (A, В, С) – плоскость S задана тремя точками. • Проекции точек, линий и других геометрических образов обозначаются теми же буквами (или цифрами), что и оригинал, но с добавлением индекса А 1, А 2, А 3 или 11, 12, 13, соответствующего плоскости проекций, на которой они получены.

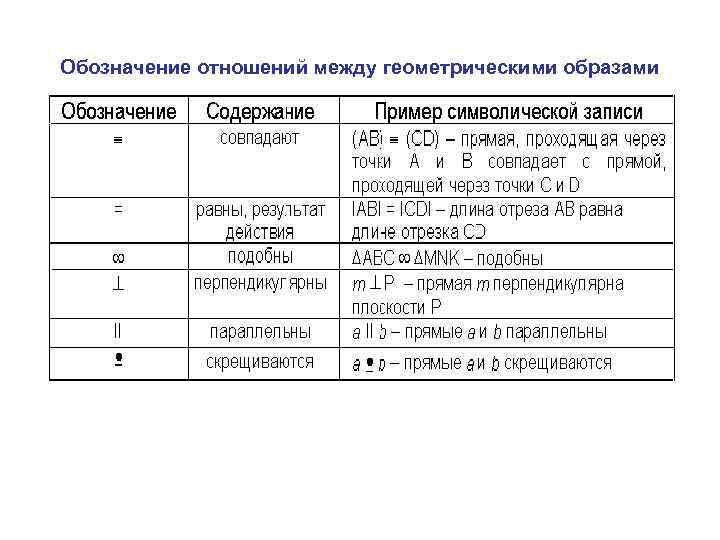Обозначение отношений между геометрическими образами

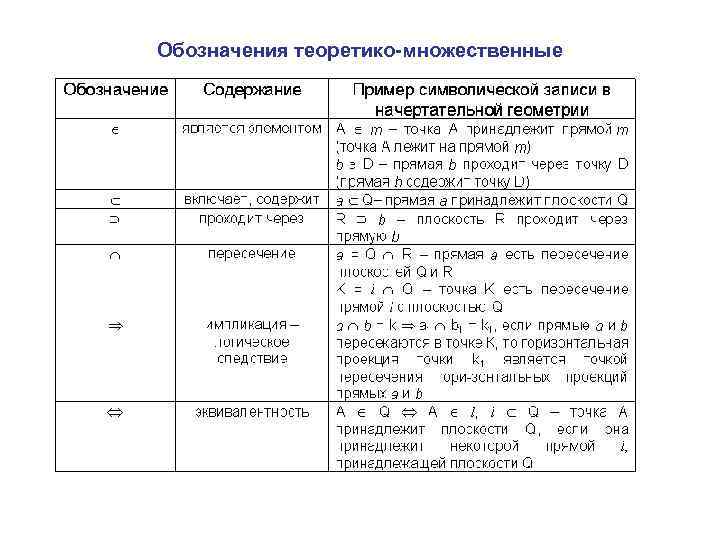Обозначения теоретико-множественные

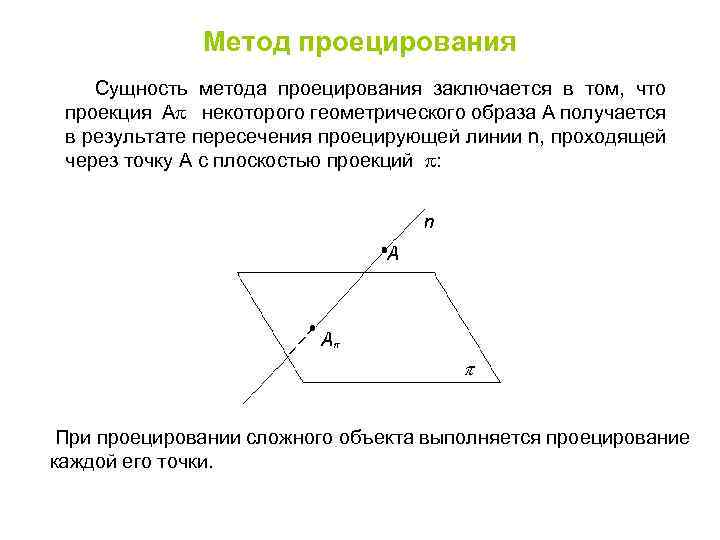Метод проецирования Сущность метода проецирования заключается в том, что проекция Аp некоторого геометрического образа А получается в результате пересечения проецирующей линии n, проходящей через точку А с плоскостью проекций p: При проецировании сложного объекта выполняется проецирование каждой его точки.

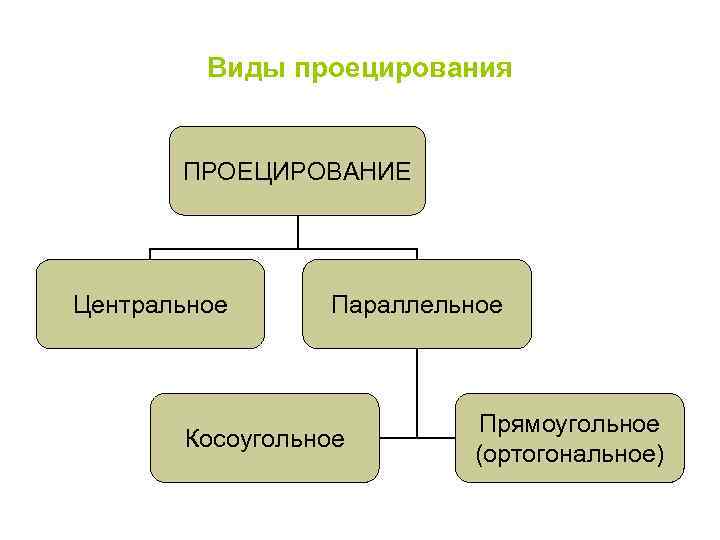Виды проецирования ПРОЕЦИРОВАНИЕ Центральное Параллельное Косоугольное Прямоугольное (ортогональное)

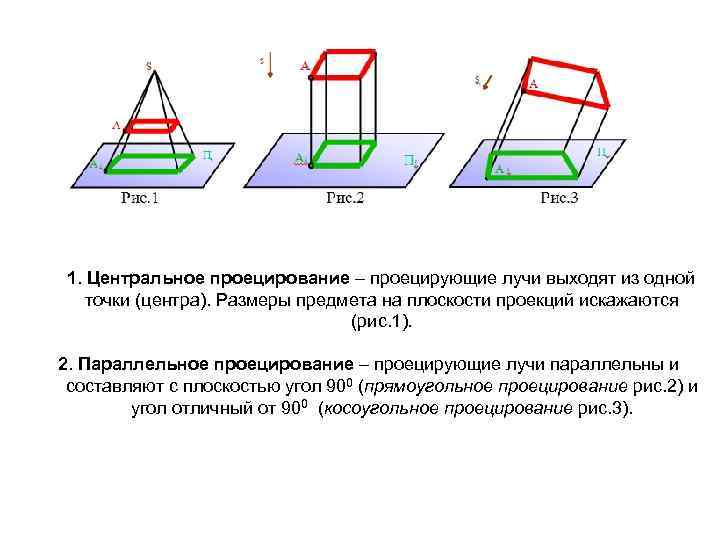1. Центральное проецирование – проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются (рис. 1). 2. Параллельное проецирование – проецирующие лучи параллельны и составляют с плоскостью угол 900 (прямоугольное проецирование рис. 2) и угол отличный от 900 (косоугольное проецирование рис. 3).

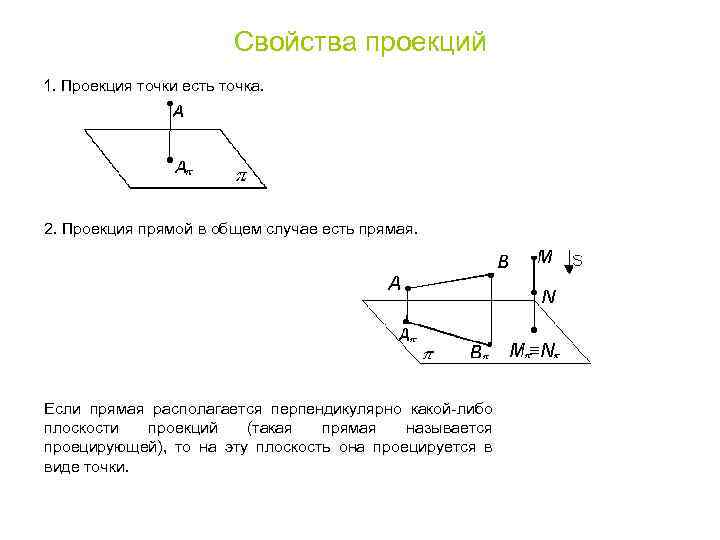Свойства проекций 1. Проекция точки есть точка. 2. Проекция прямой в общем случае есть прямая. Если прямая располагается перпендикулярно какой-либо плоскости проекций (такая прямая называется проецирующей), то на эту плоскость она проецируется в виде точки.

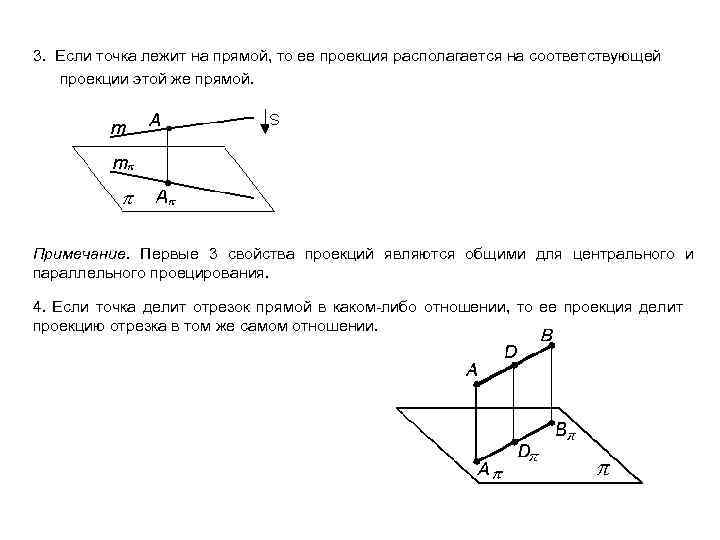3. Если точка лежит на прямой, то ее проекция располагается на соответствующей проекции этой же прямой. Примечание. Первые 3 свойства проекций являются общими для центрального и параллельного проецирования. 4. Если точка делит отрезок прямой в каком-либо отношении, то ее проекция делит проекцию отрезка в том же самом отношении.

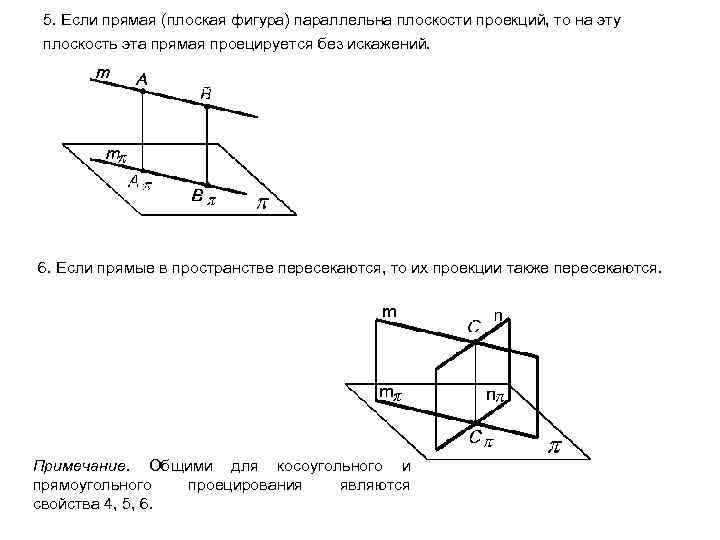5. Если прямая (плоская фигура) параллельна плоскости проекций, то на эту плоскость эта прямая проецируется без искажений. 6. Если прямые в пространстве пересекаются, то их проекции также пересекаются. Примечание. Общими для косоугольного и прямоугольного проецирования являются свойства 4, 5, 6.

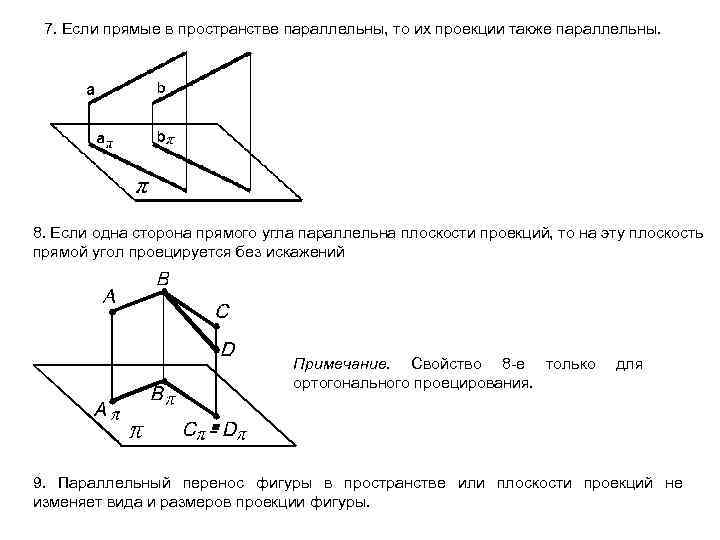7. Если прямые в пространстве параллельны, то их проекции также параллельны. 8. Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость прямой угол проецируется без искажений Примечание. Свойство 8 -е только для ортогонального проецирования. 9. Параллельный перенос фигуры в пространстве или плоскости проекций не изменяет вида и размеров проекции фигуры.

Обратимость чертежа • Рассмотренный ранее способ проецирования на одну плоскость проекций дает возможность решить прямую задачу (имея предмет, можно найти его проекцию), но не позволяет решить обратную задачу (имея проекцию, определить форму и размеры предмета). • Чертеж должен быть “обратимым”, т. е. вполне определяющим проецируемые геометрические образы (объекты). • Далее будут рассмотрены чертежи, получаемые ортогональным проецированием на две взаимно перпендикулярные плоскости проекций, т. е. комплексные чертежи (метод Монжа). Данный метод позволяет определить место каждой точки изображения относительно других точек.

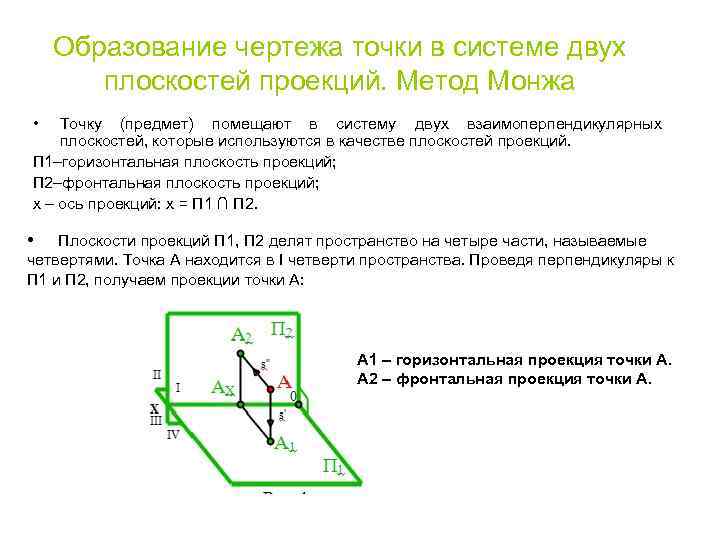Образование чертежа точки в системе двух плоскостей проекций. Метод Монжа • Точку (предмет) помещают в систему двух взаимоперпендикулярных плоскостей, которые используются в качестве плоскостей проекций. П 1–горизонтальная плоскость проекций; П 2–фронтальная плоскость проекций; х – ось проекций: х = П 1 ∩ П 2. • Плоскости проекций П 1, П 2 делят пространство на четыре части, называемые четвертями. Точка А находится в I четверти пространства. Проведя перпендикуляры к П 1 и П 2, получаем проекции точки А: А 1 – горизонтальная проекция точки А. А 2 – фронтальная проекция точки А.

• Если даны проекции А 1 и А 2 некоторой точки А, то проведя перпендикуляры: через т. А 1 к плоскости П 1 (s’ ┴ П 1), а через т. А 2 к П 2 (s” ┴ П 2) , получим в пересечении этих прямых определенную точку А (s’ ∩ s” = A). Вывод: Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.

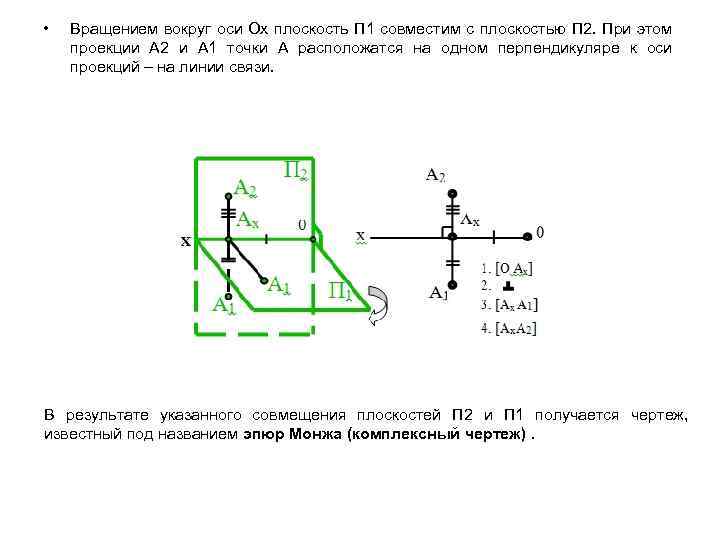• Вращением вокруг оси Ох плоскость П 1 совместим с плоскостью П 2. При этом проекции А 2 и А 1 точки А расположатся на одном перпендикуляре к оси проекций – на линии связи. В результате указанного совмещения плоскостей П 2 и П 1 получается чертеж, известный под названием эпюр Монжа (комплексный чертеж).

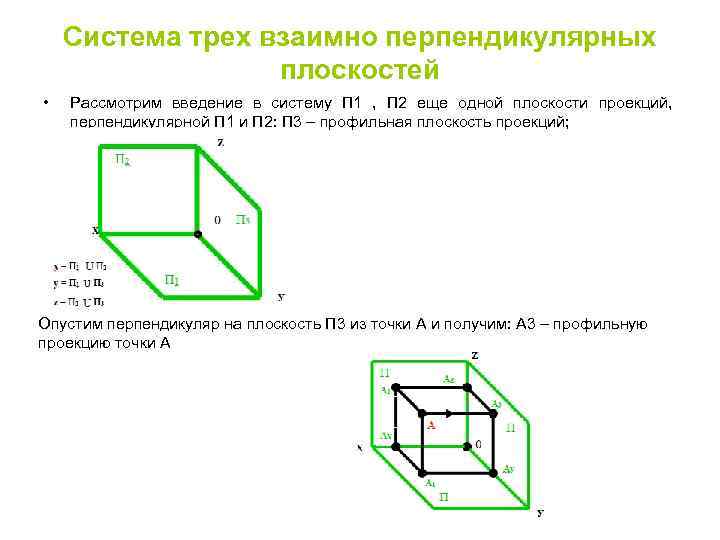Система трех взаимно перпендикулярных плоскостей • Рассмотрим введение в систему П 1 , П 2 еще одной плоскости проекций, перпендикулярной П 1 и П 2: П 3 – профильная плоскость проекций; Опустим перпендикуляр на плоскость П 3 из точки А и получим: А 3 – профильную проекцию точки А

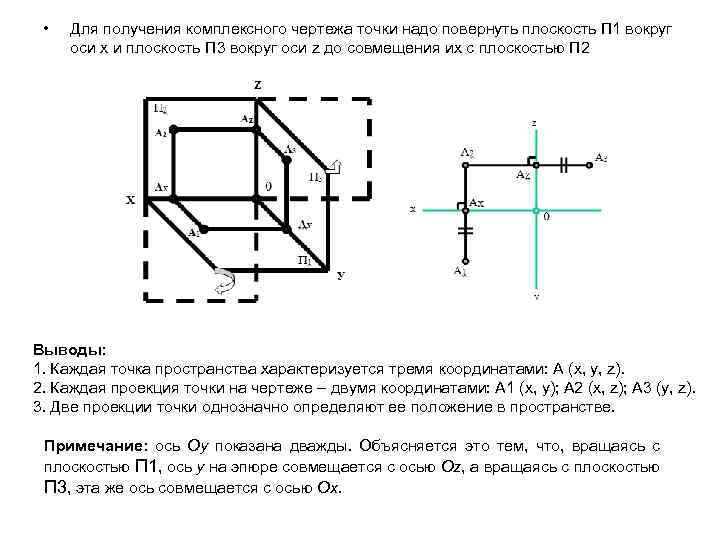• Для получения комплексного чертежа точки надо повернуть плоскость П 1 вокруг оси x и плоскость П 3 вокруг оси z до совмещения их с плоскостью П 2 Выводы: 1. Каждая точка пространства характеризуется тремя координатами: А (х, у, z). 2. Каждая проекция точки на чертеже – двумя координатами: А 1 (х, у); А 2 (х, z); А 3 (у, z). 3. Две проекции точки однозначно определяют ее положение в пространстве. Примечание: ось Оy показана дважды. Объясняется это тем, что, вращаясь с плоскостью П 1, ось y на эпюре совмещается с осью Оz, а вращаясь с плоскостью П 3, эта же ось совмещается с осью Оx.

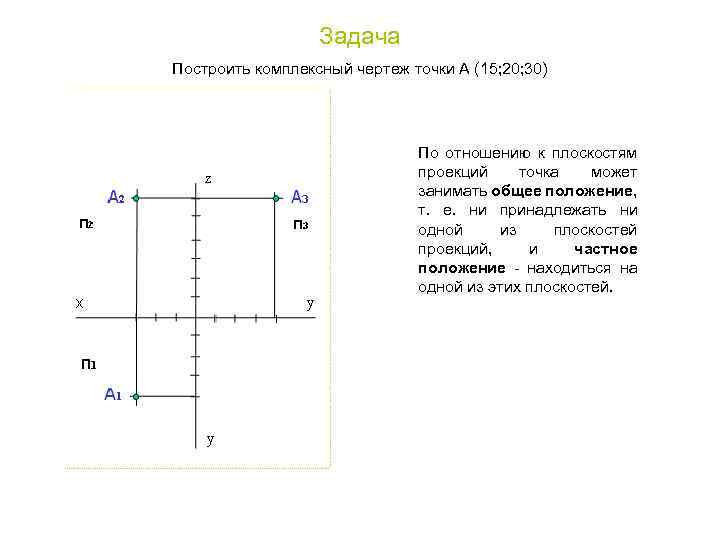Задача Построить комплексный чертеж точки А (15; 20; 30) По отношению к плоскостям проекций точка может занимать общее положение, т. е. ни принадлежать ни одной из плоскостей проекций, и частное положение - находиться на одной из этих плоскостей.

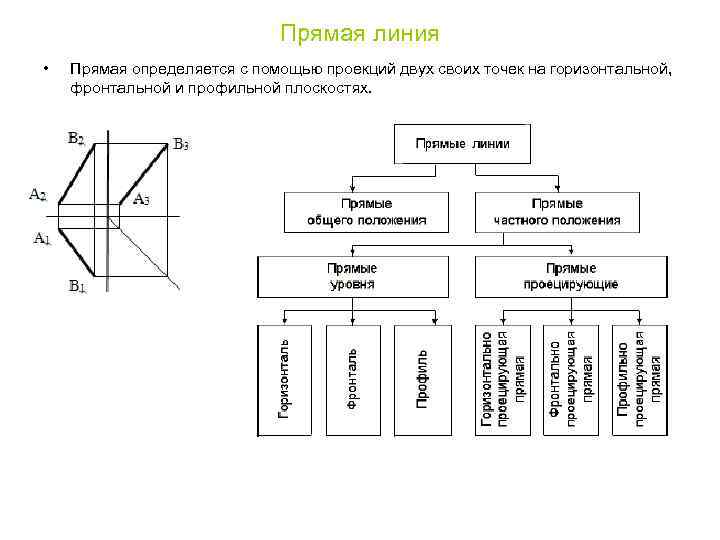Прямая линия • Прямая определяется с помощью проекций двух своих точек на горизонтальной, фронтальной и профильной плоскостях.

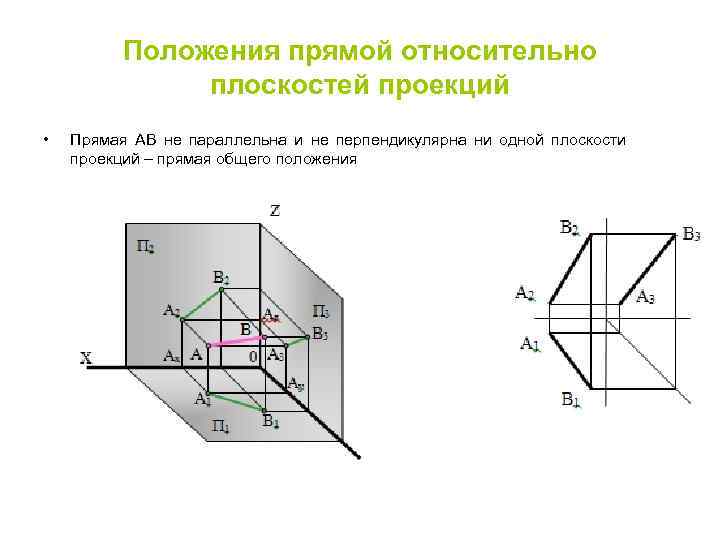Положения прямой относительно плоскостей проекций • Прямая АВ не параллельна и не перпендикулярна ни одной плоскости проекций – прямая общего положения

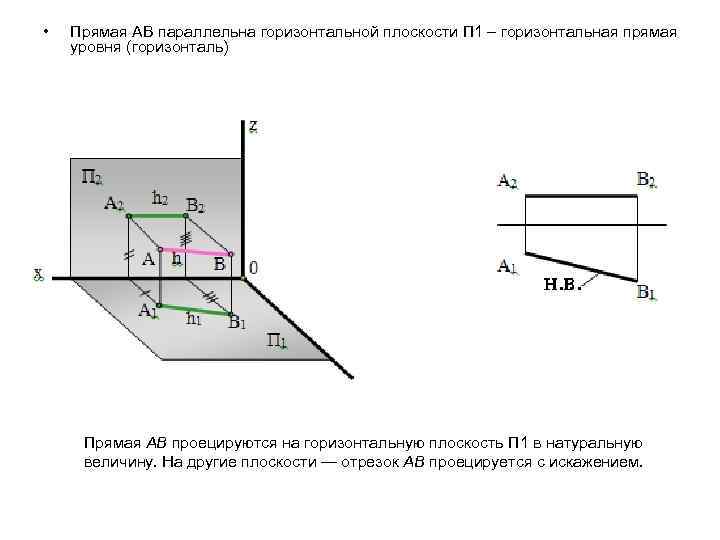• Прямая АВ параллельна горизонтальной плоскости П 1 – горизонтальная прямая уровня (горизонталь) Прямая АВ проецируются на горизонтальную плоскость П 1 в натуральную величину. На другие плоскости — отрезок АВ проецируется с искажением.

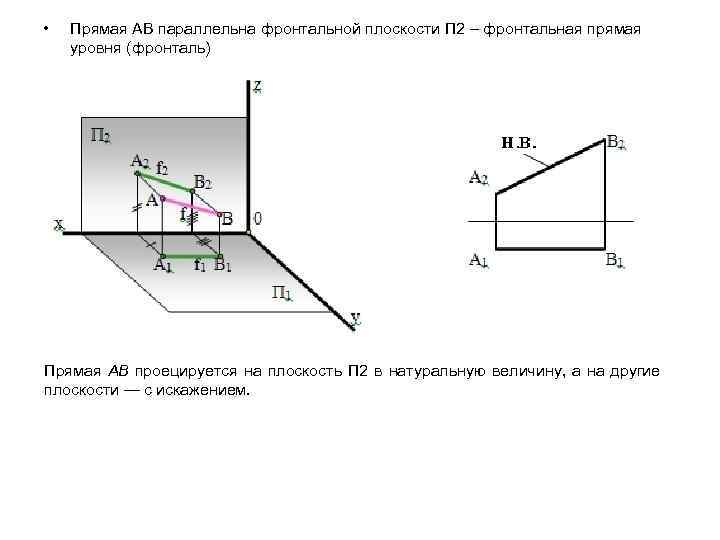• Прямая АВ параллельна фронтальной плоскости П 2 – фронтальная прямая уровня (фронталь) Прямая АВ проецируется на плоскость П 2 в натуральную величину, а на другие плоскости — с искажением.

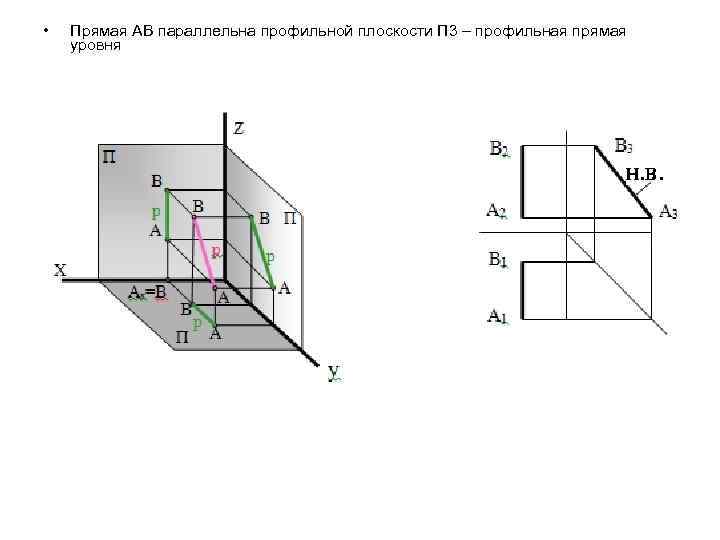• Прямая АВ параллельна профильной плоскости П 3 – профильная прямая уровня

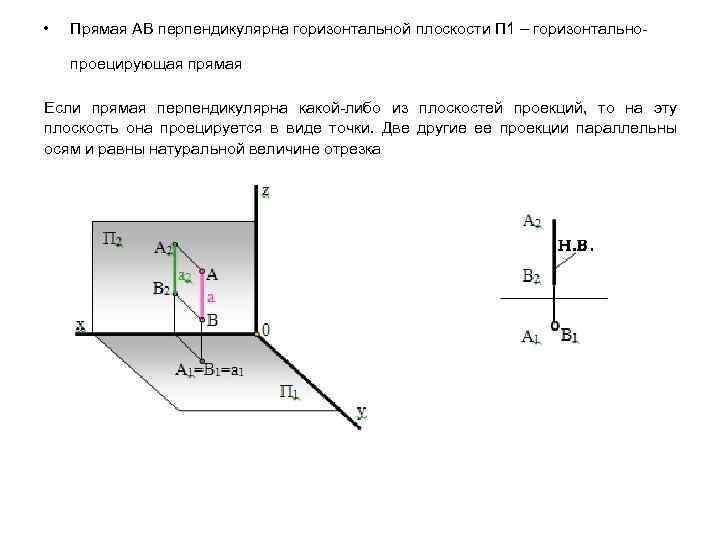• Прямая АВ перпендикулярна горизонтальной плоскости П 1 – горизонтальнопроецирующая прямая Если прямая перпендикулярна какой-либо из плоскостей проекций, то на эту плоскость она проецируется в виде точки. Две другие ее проекции параллельны осям и равны натуральной величине отрезка

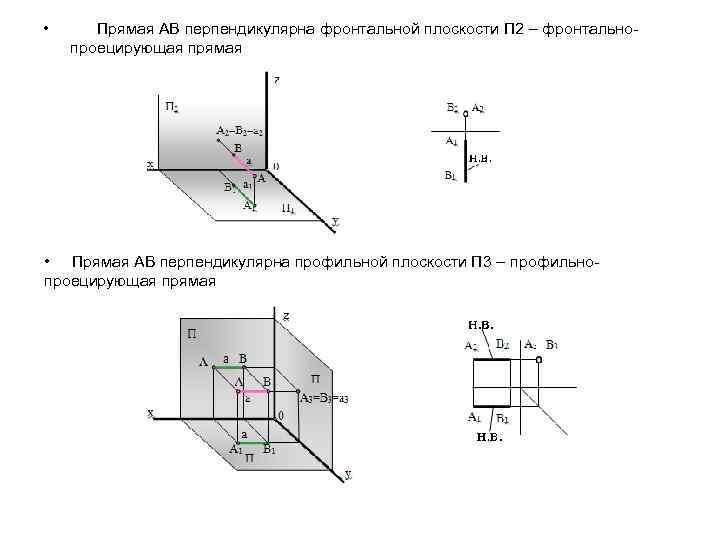• Прямая АВ перпендикулярна фронтальной плоскости П 2 – фронтальнопроецирующая прямая • Прямая АВ перпендикулярна профильной плоскости П 3 – профильно- проецирующая прямая

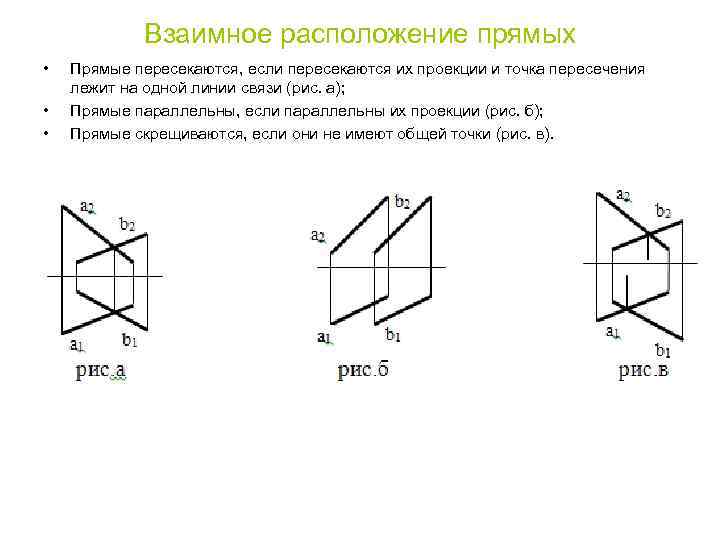Взаимное расположение прямых • • • Прямые пересекаются, если пересекаются их проекции и точка пересечения лежит на одной линии связи (рис. а); Прямые параллельны, если параллельны их проекции (рис. б); Прямые скрещиваются, если они не имеют общей точки (рис. в).

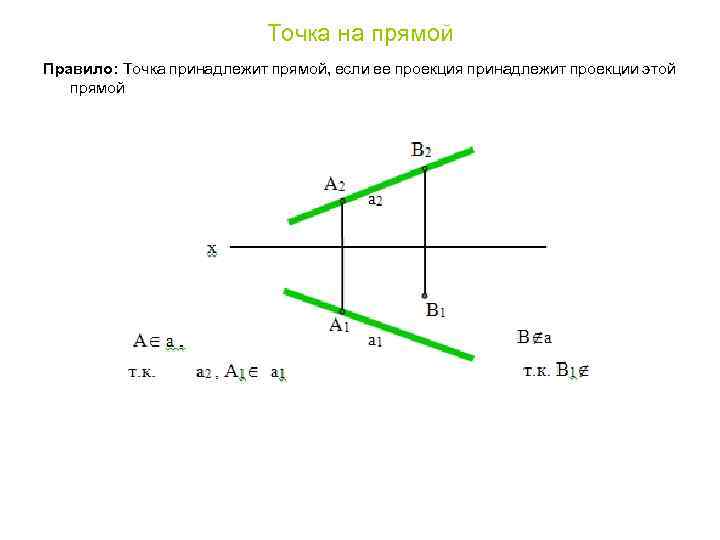Точка на прямой Правило: Точка принадлежит прямой, если ее проекция принадлежит проекции этой прямой

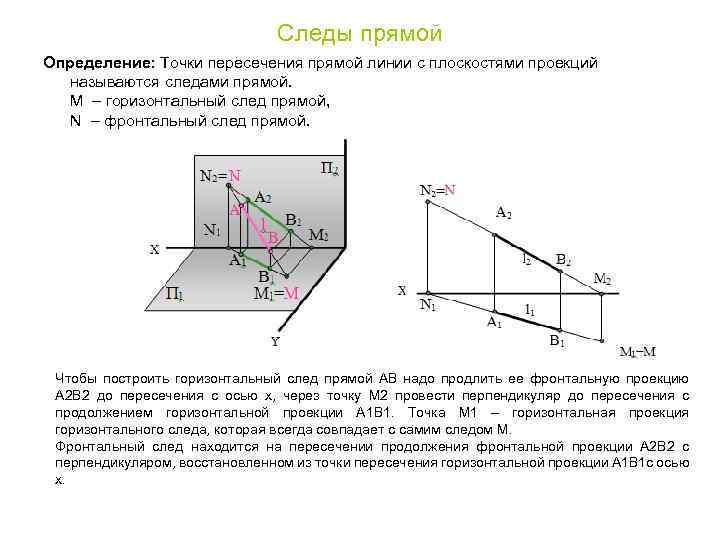Следы прямой Определение: Точки пересечения прямой линии с плоскостями проекций называются следами прямой. М – горизонтальный след прямой, N – фронтальный след прямой. Чтобы построить горизонтальный след прямой АВ надо продлить ее фронтальную проекцию А 2 В 2 до пересечения с осью x, через точку М 2 провести перпендикуляр до пересечения с продолжением горизонтальной проекции А 1 В 1. Точка М 1 – горизонтальная проекция горизонтального следа, которая всегда совпадает с самим следом М. Фронтальный след находится на пересечении продолжения фронтальной проекции А 2 В 2 с перпендикуляром, восстановленном из точки пересечения горизонтальной проекции А 1 В 1 с осью x.

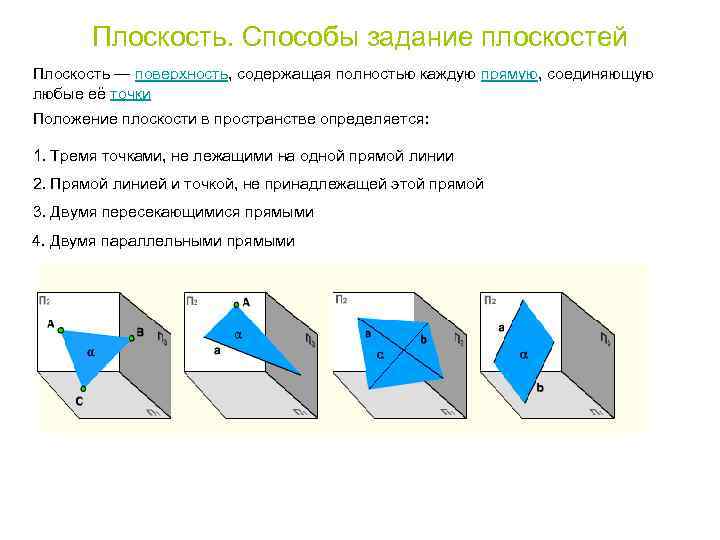Плоскость. Способы задание плоскостей Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки Положение плоскости в пространстве определяется: 1. Тремя точками, не лежащими на одной прямой линии 2. Прямой линией и точкой, не принадлежащей этой прямой 3. Двумя пересекающимися прямыми 4. Двумя параллельными прямыми

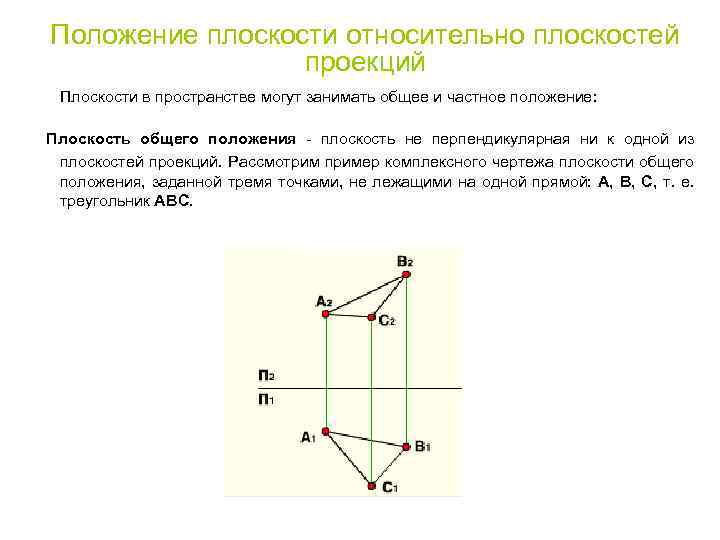Положение плоскости относительно плоскостей проекций Плоскости в пространстве могут занимать общее и частное положение: Плоскость общего положения - плоскость не перпендикулярная ни к одной из плоскостей проекций. Рассмотрим пример комплексного чертежа плоскости общего положения, заданной тремя точками, не лежащими на одной прямой: А, В, С, т. е. треугольник АВС.

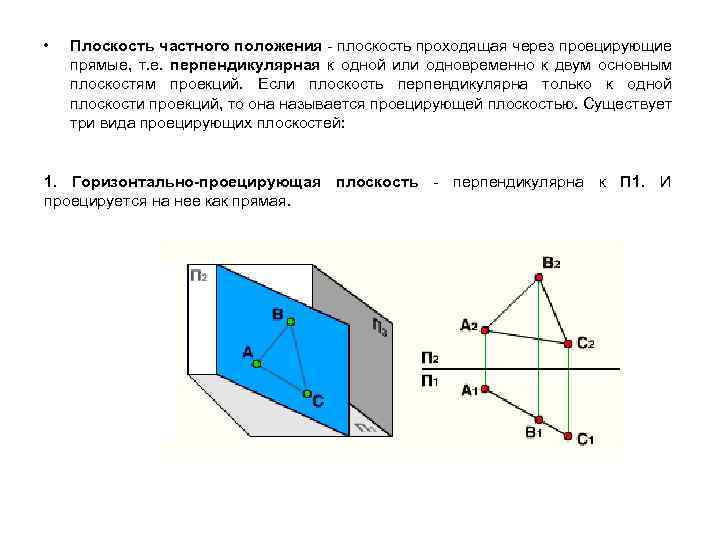• Плоскость частного положения - плоскость проходящая через проецирующие прямые, т. е. перпендикулярная к одной или одновременно к двум основным плоскостям проекций. Если плоскость перпендикулярна только к одной плоскости проекций, то она называется проецирующей плоскостью. Существует три вида проецирующих плоскостей: 1. Горизонтально-проецирующая плоскость - перпендикулярна к П 1. И проецируется на нее как прямая.

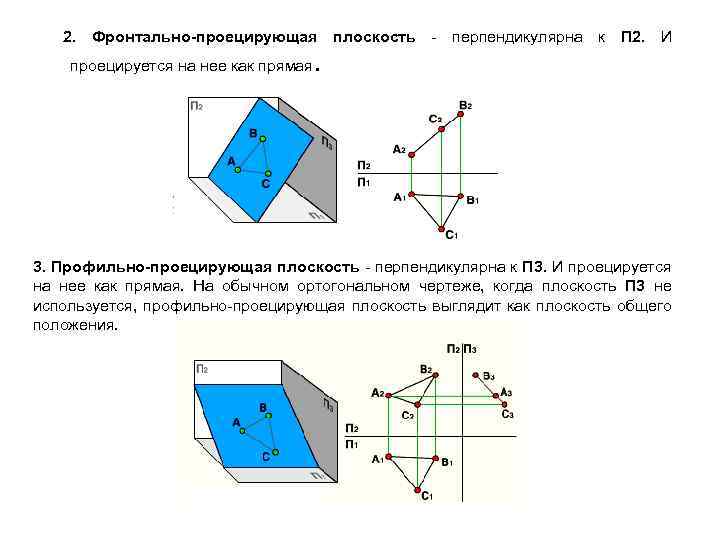2. Фронтально-проецирующая плоскость - перпендикулярна к П 2. И проецируется на нее как прямая . 3. Профильно-проецирующая плоскость - перпендикулярна к П 3. И проецируется на нее как прямая. На обычном ортогональном чертеже, когда плоскость П 3 не используется, профильно-проецирующая плоскость выглядит как плоскость общего положения.

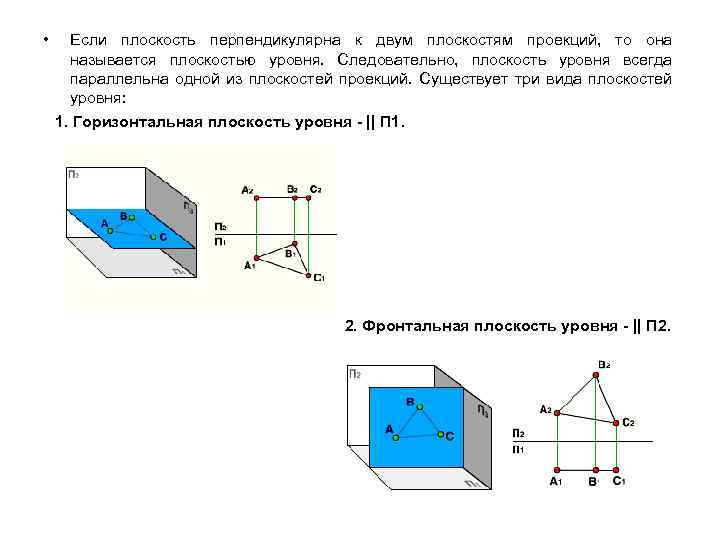• Если плоскость перпендикулярна к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций. Существует три вида плоскостей уровня: 1. Горизонтальная плоскость уровня - || П 1. 2. Фронтальная плоскость уровня - || П 2.

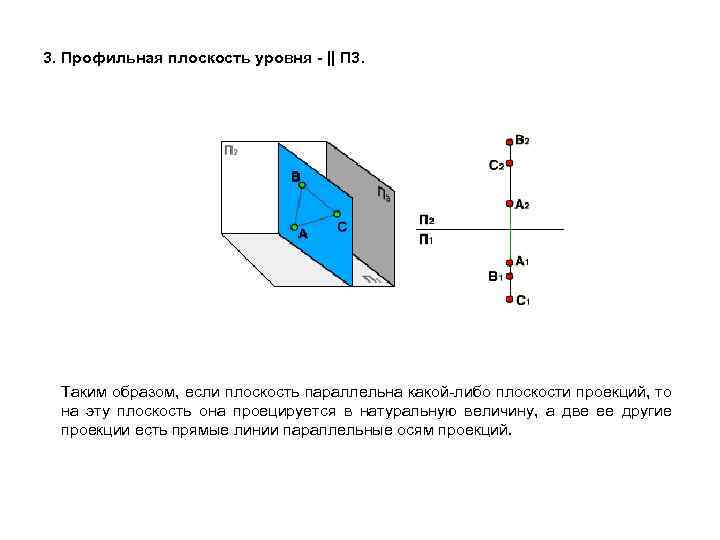3. Профильная плоскость уровня - || П 3. Таким образом, если плоскость параллельна какой-либо плоскости проекций, то на эту плоскость она проецируется в натуральную величину, а две ее другие проекции есть прямые линии параллельные осям проекций.

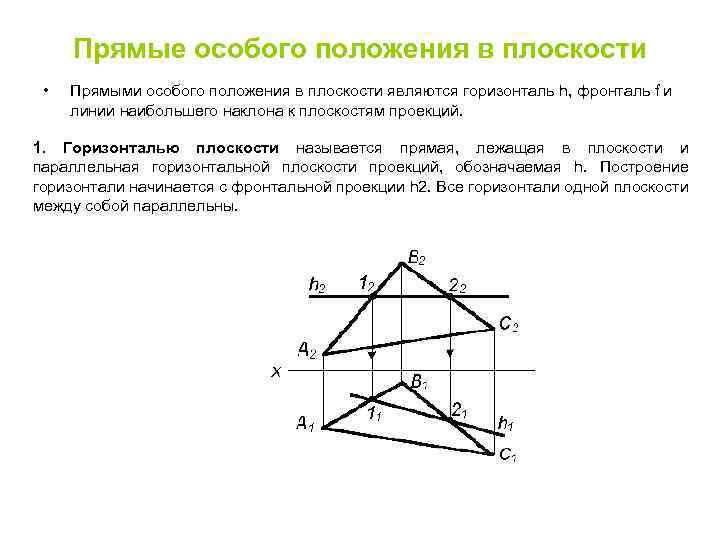Прямые особого положения в плоскости • Прямыми особого положения в плоскости являются горизонталь h, фронталь f и линии наибольшего наклона к плоскостям проекций. 1. Горизонталью плоскости называется прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций, обозначаемая h. Построение горизонтали начинается с фронтальной проекции h 2. Все горизонтали одной плоскости между собой параллельны.

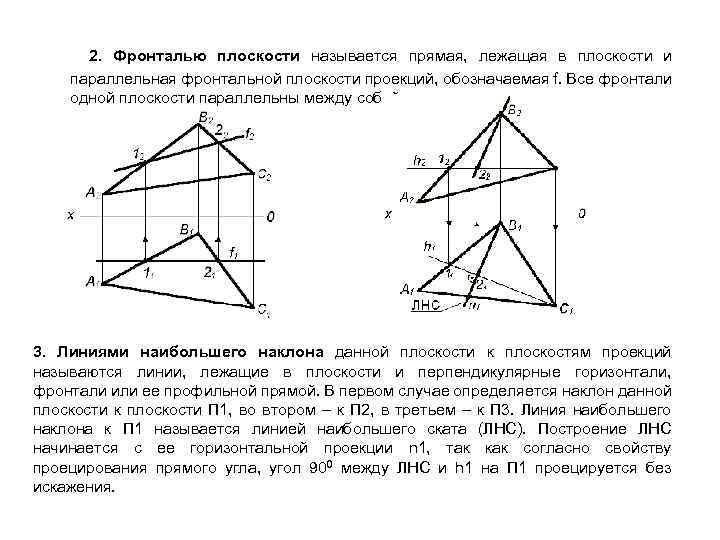2. Фронталью плоскости называется прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций, обозначаемая f. Все фронтали одной плоскости параллельны между собой. 3. Линиями наибольшего наклона данной плоскости к плоскостям проекций называются линии, лежащие в плоскости и перпендикулярные горизонтали, фронтали или ее профильной прямой. В первом случае определяется наклон данной плоскости к плоскости П 1, во втором – к П 2, в третьем – к П 3. Линия наибольшего наклона к П 1 называется линией наибольшего ската (ЛНС). Построение ЛНС начинается с ее горизонтальной проекции n 1, так как согласно свойству проецирования прямого угла, угол 900 между ЛНС и h 1 на П 1 проецируется без искажения.

Позиционные задачи • Под позиционными задачами будем понимать задачи по определению общих элементов геометрических фигур. К ним относятся задачи на принадлежность и задачи на пересечение геометрических фигур. • Задачами на принадлежность являются задачи на построение проекций: точек на линии или поверхности, линий на поверхности, линий и поверхностей, проходящих через заданные точки и линии. • В этом разделе будут рассмотрены методы решения задач на примере прямых линий и плоскостей.

Прямая и точка в плоскости В пространстве прямая может либо принадлежать плоскости, либо не принадлежать плоскости. Это утверждение справедливо и для точки. Прямая принадлежит плоскости, если она проходит: • Через две точки, принадлежащие плоскости; • Через точку плоскости параллельно любой прямой этой плоскости. Точка принадлежит плоскости, если она расположена на прямой (кривой), лежащей в данной плоскости.

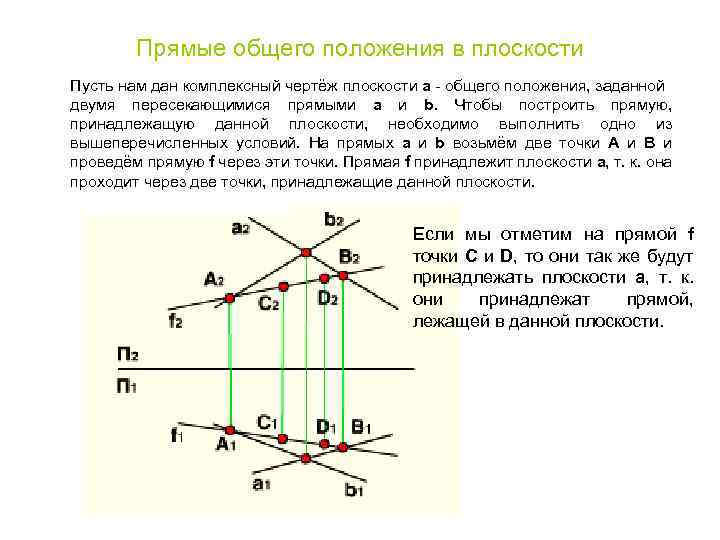Прямые общего положения в плоскости Пусть нам дан комплексный чертёж плоскости a - общего положения, заданной двумя пересекающимися прямыми а и b. Чтобы построить прямую, принадлежащую данной плоскости, необходимо выполнить одно из вышеперечисленных условий. На прямых a и b возьмём две точки А и В и проведём прямую f через эти точки. Прямая f принадлежит плоскости a, т. к. она проходит через две точки, принадлежащие данной плоскости. Если мы отметим на прямой f точки С и D, то они так же будут принадлежать плоскости a, т. к. они принадлежат прямой, лежащей в данной плоскости.

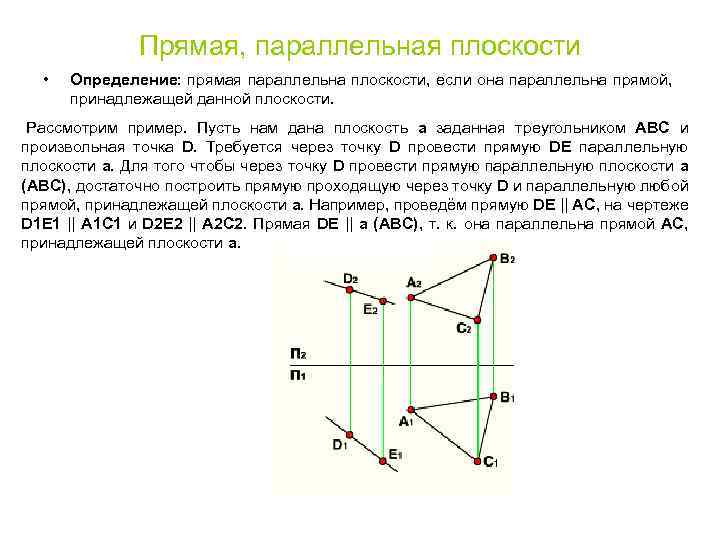Прямая, параллельная плоскости • Определение: прямая параллельна плоскости, если она параллельна прямой, принадлежащей данной плоскости. Рассмотрим пример. Пусть нам дана плоскость a заданная треугольником АВС и произвольная точка D. Требуется через точку D провести прямую DE параллельную плоскости a. Для того чтобы через точку D провести прямую параллельную плоскости a (АВС), достаточно построить прямую проходящую через точку D и параллельную любой прямой, принадлежащей плоскости a. Например, проведём прямую DE || AC, на чертеже D 1 E 1 || А 1 С 1 и D 2 E 2 || А 2 С 2. Прямая DE || a (АВС), т. к. она параллельна прямой АС, принадлежащей плоскости a.

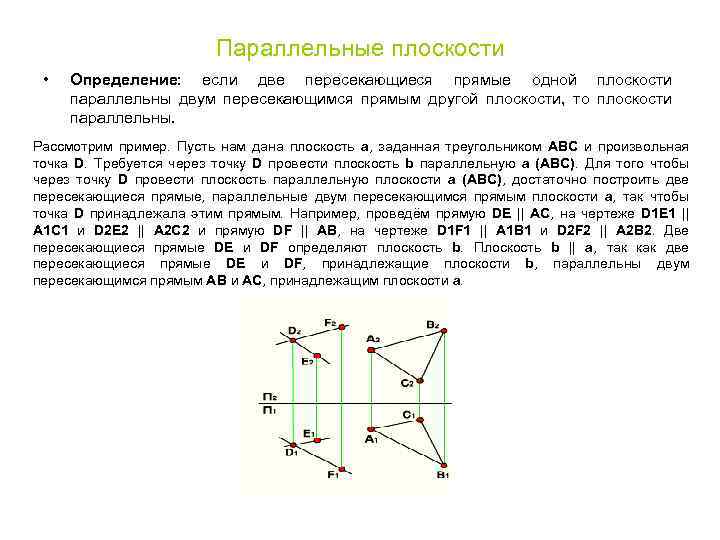Параллельные плоскости • Определение: еcли две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то плоскости параллельны. Рассмотрим пример. Пусть нам дана плоскость a, заданная треугольником АВС и произвольная точка D. Требуется через точку D провести плоскость b параллельную a (АВС). Для того чтобы через точку D провести плоскость параллельную плоскости a (АВС), достаточно построить две пересекающиеся прямые, параллельные двум пересекающимся прямым плоскости a, так чтобы точка D принадлежала этим прямым. Например, проведём прямую DE || AC, на чертеже D 1 E 1 || А 1 С 1 и D 2 E 2 || А 2 С 2 и прямую DF || AB, на чертеже D 1 F 1 || А 1 B 1 и D 2 F 2 || А 2 B 2. Две пересекающиеся прямые DE и DF определяют плоскость b. Плоскость b || a, так как две пересекающиеся прямые DE и DF, принадлежащие плоскости b, параллельны двум пересекающимся прямым АВ и АС, принадлежащим плоскости a.

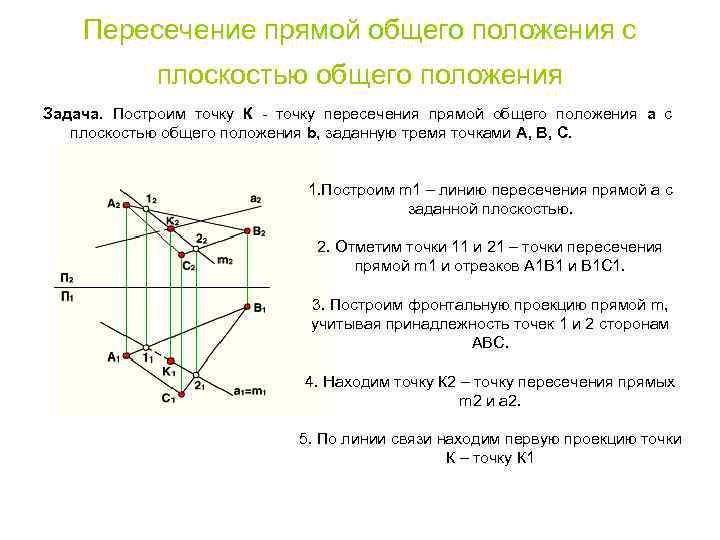Пересечение прямой общего положения с плоскостью общего положения Задача. Построим точку К - точку пересечения прямой общего положения а с плоскостью общего положения b, заданную тремя точками А, В, С. 1. Построим m 1 – линию пересечения прямой a с заданной плоскостью. 2. Отметим точки 11 и 21 – точки пересечения прямой m 1 и отрезков А 1 В 1 и В 1 С 1. 3. Построим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам АВС. 4. Находим точку К 2 – точку пересечения прямых m 2 и а 2. 5. По линии связи находим первую проекцию точки К – точку К 1

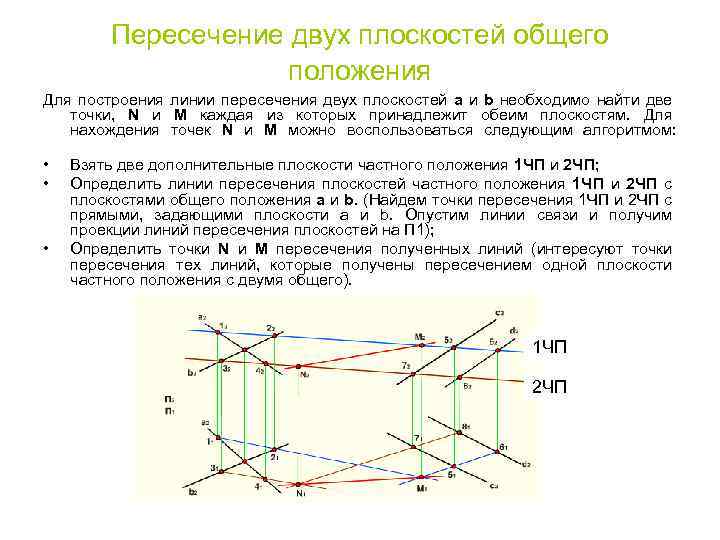Пересечение двух плоскостей общего положения Для построения линии пересечения двух плоскостей a и b необходимо найти две точки, N и M каждая из которых принадлежит обеим плоскостям. Для нахождения точек N и M можно воспользоваться следующим алгоритмом: • • • Взять две дополнительные плоскости частного положения 1 ЧП и 2 ЧП; Определить линии пересечения плоскостей частного положения 1 ЧП и 2 ЧП с плоскостями общего положения a и b. (Найдем точки пересечения 1 ЧП и 2 ЧП с прямыми, задающими плоскости a и b. Опустим линии связи и получим проекции линий пересечения плоскостей на П 1); Определить точки N и M пересечения полученных линий (интересуют точки пересечения тех линий, которые получены пересечением одной плоскости частного положения с двумя общего). 1 ЧП 2 ЧП