Понятие предела функции y=f(x) связано с понятием

Понятие предела функции y=f(x) связано с понятием предела числовой последовательности )(nfan У числовой последовательности переменная n, возрастая, принимает только целые значения, а у функции переменная х может принимать любые значения.

Axf )( Axf x )(lim. Число А называется пределом функции у= f(x) , при х стремящемся к бесконечности, если для любого, сколь угодно малого числа ε >0 , найдется такое положительное число S , что при всех |x|>S , выполняется неравенство:

При достаточно больших по модулю значениях х , значения функции f(x) очень мало отличаются от числа А (меньше, чем на число ε , каким бы малым оно не было).

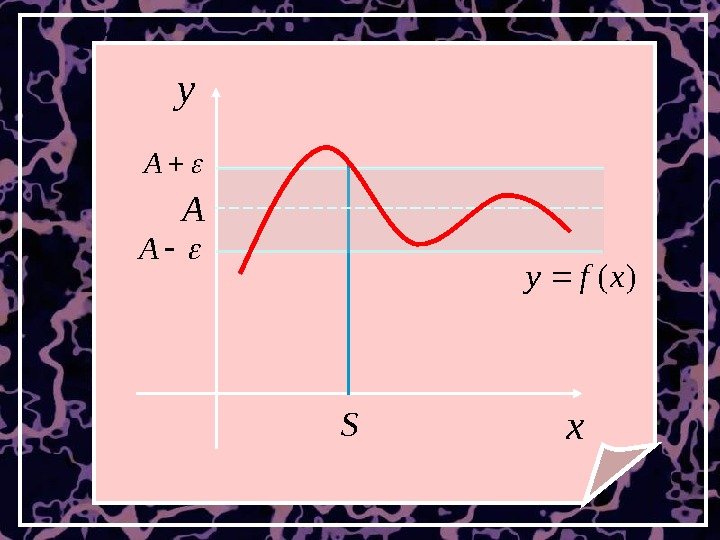
Рассмотрим геометрический смысл этого определения. Неравенство равносильно двойному неравенству Axf )( Axf. A)( что соответствует расположению части графика у= f(x) в полосе шириной 2 ε.

xy. A A A S )(xfy

Т. е. число А есть предел функции Ay. A какой бы узкой она не была. если для любого, сколь угодно малого числа ε >0 , найдется такое число S , что при всех )(xfy соответствующие ординаты графика функции у= f(x) будут заключены в полосе Sx

Доказать, что 515 lim xx x

Т. е. для любого ε >0 существует число 01 S Такое, что для всех х , таких что | x|>S , выполняется неравенство: 5)(xf 5 15 lim)(lim x x xf xx x 1 1 x 51 5 x. Для любого ε >0 515 xx

Рассмотренное определение предела при x стремящемся к бесконечности предполагает неограниченное возрастание x по абсолютной величине. Можно сформулировать понятие предела при стремлении x к бесконечности любого знака, т. е. при xx

В случае, когда неравенство. Axf)( должно выполняться при всех x таких, что х >s. x В случае, когда неравенство Axf)( должно выполняться при всех x таких, что х <-s. x Перейдем к понятию предела функции в точке. Рассмотрим некоторую функцию у= f(x). Пусть эта функция задана в некоторой окрестности точки x 0 , кроме, может быть, самой этой точки.

Axf)( Axfxx )(lim 0 Число А называется пределом функции у= f(x) , при х→ x 0 , ( или в точке x 0 ) если для любого, сколь угодно малого числа ε >0 , найдется такое положительное число δ , что при всех |x — x 0 |< δ , выполняется неравенство:

При всех значениях х, достаточно близких к x 0 , значения функции у= f(x) очень мало отличаются по абсолютной величине от числа А (меньше, чем на число ε , каким бы малым оно не было).

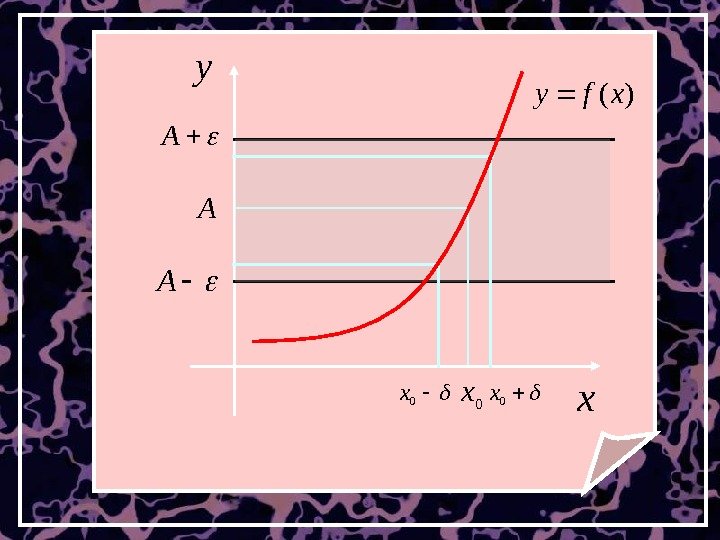
Неравенство равносильно двойному неравенству Axf )( Axf. A)( Аналогично неравенство 0 xx равносильно неравенству 00 xxx Это соответствует расположению части графика в полосе шириной 2 ε и попаданию точки х в δ -окрестность точки x 0. )(xfy

Т. е. число А есть предел функции при х → x 0 , если для любого, сколь угодно малого числа)(xfy 0 какой бы узкой она не была. Ay. Aнайдется такая δ –окрестность точки x 0 , что для всех х ≠ x 0 из этой окрестности соответствующие ординаты графика функции будут заключены в полосе )(xfy

x y )(xfy A 0 x A A 0 x 0 x

Доказать, что 5)32(lim 1 x x

Пусть ε = 0. 11. 0532 x Тогда неравенство будет выполняться при 05. 01 x Аналогично, при ε = 0. 01 Неравенство будет выполняться при 005. 01 x

Т. е. для любого ε >0 неравенство выполняется при 532 x 2 1 x Т. е. для любого ε >0 существует число 0 2 что для всех х, таких что | x -1 |< δ , выполняется неравенство: 5)(xf 5)32(lim)(lim 11 xxf xx

Определение предела не требует существования функции в самой точке x 0 , т. к. рассматриваются значения функции в некоторой окрестности точки x 0. Т. е. рассматривая предел)(lim 0 xf xx мы предполагаем, что 0 xx но не достигает значения x 0.

переменная x принимает значения только меньше x 0 или, наоборот, больше x 0 , и при этом функция f(x) стремится к некоторому числу А, то говорят об односторонних пределах соответственно справа и слева: Axf xx )(lim 00 Если при 0 xx Axf xx )(lim

Определение этих пределов будет аналогично рассмотренному выше при Вместо значений x , удовлетворяющих условию рассматриваются такие x , что 0 xx при 00 xxx 00 xx и значения x , такие что 00 xxx при 0 0 xx

Если пределы функции f(x) слева и справа одинаковы и равны А , то существует общий предел этой функции, также равный А : Axfxf xxxx )(lim 0000 Axf xx )(lim